AIEEE 2003
Paper was held on
Sat, Apr 26, 2003 9:30 AM
Chemistry
1
Which one of the following statements is not true?
2
The internal energy change when a system goes from state A to B is 40 kJ/mole. If the system goes from A to B by a reversible path and returns to state A by an irreversible path what would be the net change in internal energy?
3
If at 298 K the bond energies of C - H, C - C, C = C and H - H bonds are respectively 414, 347, 615 and 435 kJ/mol, the value of enthalpy change for the reaction
H2C = CH2(g) + H2(g) $$\to$$ H3C - CH3(g) at 298 K will be :
H2C = CH2(g) + H2(g) $$\to$$ H3C - CH3(g) at 298 K will be :
4
In an irreversible process taking place at constant T and P and in which only pressure-volume work is being done, the change in Gibbs free energy (dG) and change in entropy (dS), satisfy the criteria :
5
The correct relationship between free energy change in a reaction and the corresponding equilibrium constant Kc is :
6
The enthalpy change for a reaction does not depend upon :
7
The solubility in water of a sparingly soluble salt AB2 is 1.0 $$\times$$ 10-5 mol L-1. Its solubility product number will be :
8
Consider the reaction equilibrium
2 SO2 (g) + O2 (g) $$\leftrightharpoons$$ 2 SO3 (g); $$\Delta H^o$$ = -198 kJ
One the basis of Le Chatelier's principle, the condition favourable for the forward reaction is :
2 SO2 (g) + O2 (g) $$\leftrightharpoons$$ 2 SO3 (g); $$\Delta H^o$$ = -198 kJ
One the basis of Le Chatelier's principle, the condition favourable for the forward reaction is :
9
For the reaction equilibrium
N2O4 (g) $$\leftrightharpoons$$ 2NO2 (g)
the concentrations of N2O4 and NO2 at equilibrium are 4.8 $$\times$$ 10-2 and 1.2 $$\times$$ 10-2 mol L-1 respectively. The value of Kc for the reaction is
N2O4 (g) $$\leftrightharpoons$$ 2NO2 (g)
the concentrations of N2O4 and NO2 at equilibrium are 4.8 $$\times$$ 10-2 and 1.2 $$\times$$ 10-2 mol L-1 respectively. The value of Kc for the reaction is
10
When rain is accompanied by a thunderstorm, the collected rain water will have a pH value :
11
The IUPAC name of CH3COCH(CH3)2 is
12
In the anion HCOO$$-$$
the two carbon-oxygen bonds are found to be of equal length. What is the reason for it?
13
The general formula CnH2nO2 could be for open chain
14
On mixing a certain alkane with chlorine and irradiating it with ultravioletlight, it forms only one
monochloroalkane. This alkane could be
15
Butene-1 may be converted to butane by reaction with
16
During dehydration of alcohols to alkenes by heating with conc. H2SO4 the initiation step is
17
When CH2 = CH - COOH is reduced with LiAlH4, the compound obtained will be
18
The correct order of increasing basic nature for the bases NH3, CH3NH2 and (CH3)2 NH is
19
Ethyl isocyanide on hydrolysis in acidic medium generates
20
Complete hydrolysis of cellulose gives
21
Which one of the following statements is correct?
22
Bottles containing C6H5l and C6H5CH2I lost their original labels. They were labelled A and B for testing A and B were separately taken in test tubes and boiled with NaOH solution. The end solution in each tube was made acidic with dilute HNO3 and then some AgNO3 solution was added. Substance B gave a yellow precipitate. Which one of the following statements is true for this experiment?
23
Among the following four structures $$i$$ to $$iv,$$
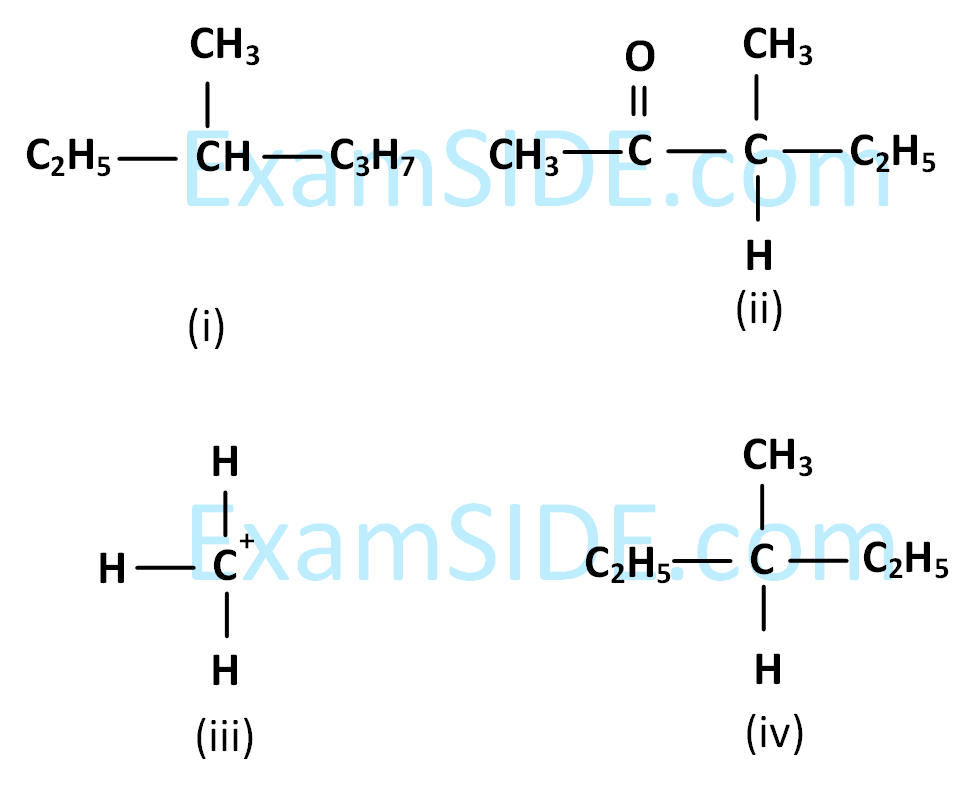
it is true that

it is true that
24
The reduction in atomic size with increase in atomic number is a characteristic of elements of
25
The atomic numbers of Vanadium (V), Chromium (cr), Manganese (Mn) and Iron (Fe), respectively, $$23,24,25$$ and $$26$$. Which one of these may be expected to have the higher second ionization enthalpy?
26
The reaction of chloroform with alcoholic $$KOH$$ and p-toluidine forms
27
The reason for double helical structure of $$DNA$$ is operation of
28
A red solid is insolvable in water. However it becomes soluble if some $$K{\rm I}$$ is added to water. Heating the red solid in a test tube results in liberation of some violet colored fumes and droplets of a metal appear on the cooler parts of the test tube. The red solid is :
29
Which one of the following substances has the highest proton affinity?
30
A pressure cooker reduces cooking time for food because
31
In a 0.2 molal aqueous solution of a weak acid HX the degree of ionization is 0.3. Taking kf for water as 1.85, the freezing point of the solution will be nearest to
32
If liquids A and B form an ideal solution
33
For a cell reaction involving a two-electron change, the standard e.m.f. of the cell is found to be 0.295 V at 25oC. The equilibrium constant of the reaction at 25oC will be
34
Standard reduction electrode potentials of three metals A,B&C are respectively +0.5 V, -3.0 V & -1.2 V. The
reducing, powers of these metals are
35
When during electrolysis of a solution of AgNO3, 9650 coulombs of charge pass through the electroplating
bath, the mass of silver deposited on the cathode will be :
36
For the redox reaction Zn(s) + Cu2+(0.1 M) $$\to$$ Zn2+(1M) + Cu(s) taking place in a cell, $$E_{cell}^o$$ is 1.10 volt. Ecell for the cell will be ($$2.303{{RT} \over F}$$ = 0.0591)
37
Several blocks of magnesium are fixed to the bottom of a ship to :
38
The radionucleide $${}_{90}^{234}Th$$ undergoes two successive $$\beta$$ -decays followed by one $$\alpha$$-decay. The atomic number
and the mass number respectively of the resulting radionucleide are
39
The half-life of a radioactive isotope is three hours. If the initial mass of the isotope were 256 g, the mass of
it remaining undecayed after 18 hours would be
40
In respect of the equation k = Ae-Ea/RT in chemical kinetics, which one of the following statements is correct?
41
The rate law for a reaction between the substances A and B is given by Rate = k[A]n [B]m On doubling the concentration of A and halving the concentration of B, the ratio of the new rate to the earlier rate of the reaction will be as
42
For the reaction system:
2NO(g) + O2(g) $$\to$$ 2NO2(g) volume is suddenly reduce to half its value by increasing the pressure on it. If the reaction is of first order with respect to O2 and second order with respect to NO, the rate of reaction will
2NO(g) + O2(g) $$\to$$ 2NO2(g) volume is suddenly reduce to half its value by increasing the pressure on it. If the reaction is of first order with respect to O2 and second order with respect to NO, the rate of reaction will
43
For making good quality mirrors, plates of float glass are used. These are obtained by floating molten glass
over a liquid metal which does not solidify before glass. The metal used can be :
44
Glass is a :
45
What would happen when a solution of potassium chromate is treated with an excess of dilute nitric acid?
46
Which one of the following nitrates will leave behind a metal on strong heating?
47
The atomic numbers of vanadium (V), Chromium (Cr), manganese (Mn) and iron (Fe) are respectively 23, 24, 25 and 26. Which one of these may be expected to have the highest second ionization enthalpy?
48
The radius of La3+ (Atomic number of La = 57) is 1.06 Å. Which one of the following given values will be
closest to the radius of Lu3+ (Atomic number of Lu = 71) ?
49
Ammonia forms the complex ion [Cu(NH3)4]2+ with copper ions in alkaline solutions but not in acidic solutions. What is the reason for it?
50
One mole of the complex compound Co(NH3)5Cl3, gives 3 moles of ions on dissolution in water. One mole of the same complex reacts with two moles of AgNO3 solution to yield two moles of AgCl (s). The structure of the complex is :
51
In the coordination compound, K4[Ni(CN)4], the oxidation state of nickel is :
52
Which one of the following compounds has the smallest bond angle in its molecule?
53
What volume of hydrogen gas at 273 K and 1 atm pressure will be consumed in obtaining 21.6 g of elemental boron (atomic mass = 10.8) from the reduction of boron trichloride by hydrogen?
54
25 ml of a solution of barium hydroxide on titration with a 0.1 molar solution of hydrochloric acid gave a litre value of 35 ml. The molarity of barium hydroxide solution was
55
The number of d-electrons retained in Fe2+ (At no of Fe = 26) ion is :
56
The orbital angular momentum for an electron revolving in an orbit is given by $$\sqrt {l(l + 1)} {h \over {2\pi }}$$. This momentum for an s-electron will be given by
57
Which one of the following groupings represents a collection of isoelectronic species? (At. nos. : Cs : 55, Br : 35)
58
In Bohr series of lines of hydrogen spectrum, the third line from the red end corresponds to which one of the following inter-orbit jumps of the electron for Bohr orbits in an atom of hydrogen
59
The de Broglie wavelength of a tennis ball of mass 60 g moving with a velocity of 10 meters per second is approximately
60
According to the Periodic Law of elements, the variation in properties of elements is related to their
61
Which one of the following is an amphoteric oxide?
62
An ethar is more volatile than an alcohol having the same molecular formula. This is due to
63
Which one of the following pairs of molecules will have permanent dipole moments for both members
64
The pair of species having identical shapes for molecules of both species is
Mathematics
1
The value of $$\mathop {\lim }\limits_{x \to 0} {{\int\limits_0^{{x^2}} {{{\sec }^2}tdt} } \over xsinx}$$ is
2
The function $$f\left( x \right)$$ $$ = \log \left( {x + \sqrt {{x^2} + 1} } \right)$$, is
3
A function $$f$$ from the set of natural numbers to integers defined by
$$$f\left( n \right) = \left\{ {\matrix{
{{{n - 1} \over 2},\,when\,n\,is\,odd} \cr
{ - {n \over 2},\,when\,n\,is\,even} \cr
} } \right.$$$
is
4
If $$f:R \to R$$ satisfies $$f$$(x + y) = $$f$$(x) + $$f$$(y), for all x, y $$ \in $$ R and $$f$$(1) = 7, then $$\sum\limits_{r = 1}^n {f\left( r \right)} $$ is
5
Domain of definition of the function f(x) = $${3 \over {4 - {x^2}}}$$ + $${\log _{10}}\left( {{x^3} - x} \right)$$, is
6
If $$\mathop {\lim }\limits_{x \to 0} {{\log \left( {3 + x} \right) - \log \left( {3 - x} \right)} \over x}$$ = k, the value of k is
7
Let $$f(a) = g(a) = k$$ and their nth derivatives
$${f^n}(a)$$, $${g^n}(a)$$ exist and are not equal for some n. Further if
$$\mathop {\lim }\limits_{x \to a} {{f(a)g(x) - f(a) - g(a)f(x) + f(a)} \over {g(x) - f(x)}} = 4$$
then the value of k is
$${f^n}(a)$$, $${g^n}(a)$$ exist and are not equal for some n. Further if
$$\mathop {\lim }\limits_{x \to a} {{f(a)g(x) - f(a) - g(a)f(x) + f(a)} \over {g(x) - f(x)}} = 4$$
then the value of k is
8
$$\mathop {\lim }\limits_{x \to {\pi \over 2}} {{\left[ {1 - \tan \left( {{x \over 2}} \right)} \right]\left[ {1 - \sin x} \right]} \over {\left[ {1 + \tan \left( {{x \over 2}} \right)} \right]{{\left[ {\pi - 2x} \right]}^3}}}$$ is
9
If $$f(x) = \left\{ {\matrix{
{x{e^{ - \left( {{1 \over {\left| x \right|}} + {1 \over x}} \right)}}} & {,x \ne 0} \cr
0 & {,x = 0} \cr
} } \right.$$
then $$f(x)$$ is
then $$f(x)$$ is
10
In an experiment with 15 observations on $$x$$, then following results were available:
$$\sum {{x^2}} = 2830$$, $$\sum x = 170$$
One observation that was 20 was found to be wrong and was replaced by the correct value 30. Then the corrected variance is :
$$\sum {{x^2}} = 2830$$, $$\sum x = 170$$
One observation that was 20 was found to be wrong and was replaced by the correct value 30. Then the corrected variance is :
11
The median of a set of 9 distinct observations is 20.5. If each of the largest 4 observations of
the set is increased by 2, then the median of the new set :
12
Five horses are in a race. Mr. A selects two of the horses at random and bets on them. The probability that Mr. A selected the winning horse is :
13
The trigonometric equation $${\sin ^{ - 1}}x = 2{\sin ^{ - 1}}a$$ has a solution for :
14
If the function $$f\left( x \right) = 2{x^3} - 9a{x^2} + 12{a^2}x + 1,$$ where $$a>0,$$ attains its maximum and minimum at $$p$$ and $$q$$ respectively such that $${p^2} = q$$ , then $$a$$ equals
15
If $$A = \left[ {\matrix{
a & b \cr
b & a \cr
} } \right]$$ and $${A^2} = \left[ {\matrix{
\alpha & \beta \cr
\beta & \alpha \cr
} } \right]$$, then
16
If $$1,$$ $$\omega ,{\omega ^2}$$ are the cube roots of unity, then
$$\Delta = \left| {\matrix{ 1 & {{\omega ^n}} & {{\omega ^{2n}}} \cr {{\omega ^n}} & {{\omega ^{2n}}} & 1 \cr {{\omega ^{2n}}} & 1 & {{\omega ^n}} \cr } } \right|$$ is equal to
17
If the system of linear equations
$$x + 2ay + az = 0;$$ $$x + 3by + bz = 0;\,\,x + 4cy + cz = 0;$$
has a non - zero solution, then $$a, b, c$$.
$$x + 2ay + az = 0;$$ $$x + 3by + bz = 0;\,\,x + 4cy + cz = 0;$$
has a non - zero solution, then $$a, b, c$$.
18
The area of the region bounded by the curves $$y = \left| {x - 1} \right|$$ and $$y = 3 - \left| x \right|$$ is :
19
Let $$f(x)$$ be a function satisfying $$f'(x)=f(x)$$ with $$f(0)=1$$ and $$g(x)$$ be a function that satisfies $$f\left( x \right) + g\left( x \right) = {x^2}$$. Then the value of the integral $$\int\limits_0^1 {f\left( x \right)g\left( x \right)dx,} $$ is
20
If $$f\left( {a + b - x} \right) = f\left( x \right)$$ then $$\int\limits_a^b {xf\left( x \right)dx} $$ is equal to
21
The value of the integral $$I = \int\limits_0^1 {x{{\left( {1 - x} \right)}^n}dx} $$ is
22
The solution of the differential equation
$$\left( {1 + {y^2}} \right) + \left( {x - {e^{{{\tan }^{ - 1}}y}}} \right){{dy} \over {dx}} = 0,$$ is :
$$\left( {1 + {y^2}} \right) + \left( {x - {e^{{{\tan }^{ - 1}}y}}} \right){{dy} \over {dx}} = 0,$$ is :
23
The degree and order of the differential equation of the family of all parabolas whose axis is $$x$$-axis, are respectively.
24
Events $$A, B, C$$ are mutually exclusive events such that $$P\left( A \right) = {{3x + 1} \over 3},$$ $$P\left( B \right) = {{1 - x} \over 4}$$ and $$P\left( C \right) = {{1 - 2x} \over 2}$$ The set of possible values of $$x$$ are in the interval.
25
If $$\overrightarrow a \times \overrightarrow b = \overrightarrow b \times \overrightarrow c = \overrightarrow c \times \overrightarrow a $$ then $$\overrightarrow a + \overrightarrow b + \overrightarrow c = $$
26
Let $$\overrightarrow u = \widehat i + \widehat j,\,\overrightarrow v = \widehat i - \widehat j$$ and $$\overrightarrow w = \widehat i + 2\widehat j + 3\widehat k\,\,.$$ If $$\widehat n$$ is a unit vector such that $$\overrightarrow u .\widehat n = 0$$ and $$\overrightarrow v .\widehat n = 0\,\,,$$ then $$\left| {\overrightarrow w .\widehat n} \right|$$ is equal to :
27
The vectors $$\overrightarrow {AB} = 3\widehat i + 4\widehat k\,\,\& \,\,\overrightarrow {AC} = 5\widehat i - 2\widehat j + 4\widehat k$$ are the sides of triangle $$ABC.$$ The length of the median through $$A$$ is :
28
The two lines $$x=ay+b,z=cy+d$$ and $$x = a'y + b',z = c'y + d'$$ will be perpendicular, if and only if :
29
The lines $${{x - 2} \over 1} = {{y - 3} \over 1} = {{z - 4} \over { - k}}$$ and $${{x - 1} \over k} = {{y - 4} \over 2} = {{z - 5} \over 1}$$ are coplanar if :
30
$$\overrightarrow a \,,\overrightarrow b \,,\overrightarrow c $$ are $$3$$ vectors, such that
$$\overrightarrow a + \overrightarrow b + \overrightarrow c = 0$$ , $$\left| {\overrightarrow a } \right| = 1\,\,\,\left| {\overrightarrow b } \right| = 2,\,\,\,\left| {\overrightarrow c } \right| = 3,$$,
then $${\overrightarrow a .\overrightarrow b + \overrightarrow b .\overrightarrow c + \overrightarrow c .\overrightarrow a }$$ is equal to :
$$\overrightarrow a + \overrightarrow b + \overrightarrow c = 0$$ , $$\left| {\overrightarrow a } \right| = 1\,\,\,\left| {\overrightarrow b } \right| = 2,\,\,\,\left| {\overrightarrow c } \right| = 3,$$,
then $${\overrightarrow a .\overrightarrow b + \overrightarrow b .\overrightarrow c + \overrightarrow c .\overrightarrow a }$$ is equal to :
31
A tetrahedron has vertices at $$O(0,0,0), A(1,2,1) B(2,1,3)$$ and $$C(-1,1,2).$$ Then the angle between the faces $$OAB$$ and $$ABC$$ will be :
32
If $$\left| {\matrix{
a & {{a^2}} & {1 + {a^3}} \cr
b & {{b^2}} & {1 + {b^3}} \cr
c & {{c^2}} & {1 + {c^3}} \cr
} } \right| = 0$$ and vectors $$\left( {1,a,{a^2}} \right),\,\,$$
$$\left( {1,b,{b^2}} \right)$$ and $$\left( {1,c,{c^2}} \right)\,$$ are non-coplanar, then the product $$abc$$ equals :
$$\left( {1,b,{b^2}} \right)$$ and $$\left( {1,c,{c^2}} \right)\,$$ are non-coplanar, then the product $$abc$$ equals :
33
Consider points $$A, B, C$$ and $$D$$ with position
vectors $$7\widehat i - 4\widehat j + 7\widehat k,\widehat i - 6\widehat j + 10\widehat k, - \widehat i - 3\widehat j + 4\widehat k$$ and $$5\widehat i - \widehat j + 5\widehat k$$ respectively. Then $$ABCD$$ is a :
vectors $$7\widehat i - 4\widehat j + 7\widehat k,\widehat i - 6\widehat j + 10\widehat k, - \widehat i - 3\widehat j + 4\widehat k$$ and $$5\widehat i - \widehat j + 5\widehat k$$ respectively. Then $$ABCD$$ is a :
34
Let $${Z_1}$$ and $${Z_2}$$ be two roots of the equation $${Z^2} + aZ + b = 0$$, Z being complex. Further , assume that the origin, $${Z_1}$$ and $${Z_2}$$ form an equilateral triangle. Then :
35
If $${\left( {{{1 + i} \over {1 - i}}} \right)^x} = 1$$ then :
36
If the sum of the roots of the quadratic equation $$a{x^2} + bx + c = 0$$ is equal to the sum of the squares of their reciprocals, then $${a \over c},\,{b \over a}$$ and $${c \over b}$$ are in
37
The value of '$$a$$' for which one root of the quadratic equation
$$$\left( {{a^2} - 5a + 3} \right){x^2} + \left( {3a - 1} \right)x + 2 = 0$$$
is twice as large as the other is
is twice as large as the other is
38
The number of real solutions of the equation $${x^2} - 3\left| x \right| + 2 = 0$$ is
39
The real number $$x$$ when added to its inverse gives the minimum sum at $$x$$ equal :
40
If $$x$$ is positive, the first negative term in the expansion of $${\left( {1 + x} \right)^{27/5}}$$ is
41
A student is to answer 10 out of 13 questions in an examination such that he must choose at least 4 from the first five questions. The number of choices available to him is
42
The number of integral terms in the expansion of $${\left( {\sqrt 3 + \root 8 \of 5 } \right)^{256}}$$ is
43
The number of ways in which 6 men and 5 women can dine at a round table if no two women are to sit together is given by
44
If $${}^n{C_r}$$ denotes the number of combination of n things taken r at a time, then the expression $$\,{}^n{C_{r + 1}} + {}^n{C_{r - 1}} + 2\, \times \,{}^n{C_r}$$ equals
45
A square of side a lies above the $$x$$-axis and has one vertex at the origin. The side passing through the origin makes an angle $$\alpha \left( {0 < \alpha < {\pi \over 4}} \right)$$ with the positive direction of x-axis. The equation of its diagonal not passing through the origin is :
46
Locus of centroid of the triangle whose vertices are $$\left( {a\cos t,a\sin t} \right),\left( {b\sin t, - b\cos t} \right)$$ and $$\left( {1,0} \right),$$ where $$t$$ is a parameter, is :
47
If $${x_1},{x_2},{x_3}$$ and $${y_1},{y_2},{y_3}$$ are both in G.P. with the same common ratio, then the points $$\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right)$$ and $$\left( {{x_3},{y_3}} \right)$$ :
48
If the equation of the locus of a point equidistant from the point $$\left( {{a_{1,}}{b_1}} \right)$$ and $$\left( {{a_{2,}}{b_2}} \right)$$ is
$$\left( {{a_1} - {a_2}} \right)x + \left( {{b_1} - {b_2}} \right)y + c = 0$$ , then the value of $$'c'$$ is :
$$\left( {{a_1} - {a_2}} \right)x + \left( {{b_1} - {b_2}} \right)y + c = 0$$ , then the value of $$'c'$$ is :
49
The lines 2x - 3y = 5 and 3x - 4y = 7 are diameters of a circle having area as 154 sq. units. Then the equation of the circle is :
50
The foci of the ellipse $${{{x^2}} \over {16}} + {{{y^2}} \over {{b^2}}} = 1$$ and the hyperbola $${{{x^2}} \over {144}} - {{{y^2}} \over {81}} = {1 \over {25}}$$ coincide. Then the value of $${b^2}$$ is :
51
If $$f\left( y \right) = {e^y},$$ $$g\left( y \right) = y;y > 0$$ and
$$F\left( t \right) = \int\limits_0^t {f\left( {t - y} \right)g\left( y \right)dy,} $$ then :
$$F\left( t \right) = \int\limits_0^t {f\left( {t - y} \right)g\left( y \right)dy,} $$ then :
52
If $$f\left( x \right) = {x^n},$$ then the value of
$$f\left( 1 \right) - {{f'\left( 1 \right)} \over {1!}} + {{f''\left( 1 \right)} \over {2!}} - {{f'''\left( 1 \right)} \over {3!}} + ..........{{{{\left( { - 1} \right)}^n}{f^n}\left( 1 \right)} \over {n!}}$$ is
53
Let $$f\left( x \right)$$ be a polynomial function of second degree. If $$f\left( 1 \right) = f\left( { - 1} \right)$$ and $$a,b,c$$ are in $$A.P, $$ then $$f'\left( a \right),f'\left( b \right),f'\left( c \right)$$ are in
54
If $$z$$ and $$\omega $$ are two non-zero complex numbers such that $$\left| {z\omega } \right| = 1$$ and $$Arg(z) - Arg(\omega ) = {\pi \over 2},$$ then $$\,\overline {z\,} \omega $$ is equal to
Physics
1
The wavelengths involved in the spectrum of deuterium $$\left( {{}_1^2\,D} \right)$$ are slightly different from that of hydrogen spectrum, because
2
If the binding energy of the electron in a hydrogen atom is $$13.6eV,$$ the energy required to remove the electron from the first excited state of $$L{i^{ + + }}$$ is
3
Which of the following atoms has the lowest ionization potential ?
4
Two identical photo-cathodes receive light of frequencies $${f_1}$$ and $${f_2}$$. If the velocities of the photo electrons (of mass $$m$$ ) coming out are respectively $${v_1}$$ and $${v_2},$$ then
5
In the nuclear fusion reaction
$$${}_1^2H + {}_1^3H \to {}_2^4He + n$$$
given that the repulsive potential energy between the two nuclei is $$ \sim 7.7 \times {10^{ - 14}}J$$, the temperature at which the gases must be heated to initiate the reaction is nearly
[ Boltzmann's Constant $$k = 1.38 \times {10^{ - 23}}\,J/K$$ ]
given that the repulsive potential energy between the two nuclei is $$ \sim 7.7 \times {10^{ - 14}}J$$, the temperature at which the gases must be heated to initiate the reaction is nearly
[ Boltzmann's Constant $$k = 1.38 \times {10^{ - 23}}\,J/K$$ ]
6
In the middle of the depletion layer of a reverse- biased $$p$$-$$n$$ junction, the
7
When the current changes from $$ + 2A$$ to $$-2A$$ in $$0.05$$ second, an $$e.m.f.$$ of $$8$$ $$V$$ is inducted in a coil. The coefficient of self- induction of the coil is
8
The length of a given cylindrical wire is increased by $$100\% $$. Due to the consequent decrease in diameter the change in the resistance of the wire will be
9
The thermo $$e.m.f.$$ of a thermo -couple is $$25$$ $$\mu V/{}^ \circ C$$ at room temperature. A galvanometer of $$40$$ $$ohm$$ resistance, capable of detecting current as low as $${10^{ - 5}}\,A,$$ is connected with the thermo couple. The smallest temperature difference that can be detected by this system is
10
An ammeter reads upto $$1$$ ampere. Its internal resistance is $$0.81$$ $$ohm$$. To increase the range to $$10$$ $$A$$ the value of the required shunt is
11
The nagative $$Zn$$ pole of a Daniell cell, sending a constant current through a circuit, decreases in mass by $$0.13g$$ in $$30$$ minutes. If the electrochemical equivalent of $$Zn$$ and $$Cu$$ are $$32.5$$ and $$31.5$$ respectively, the increase in the mass of the positive $$Cu$$ pole in this time is
12
A $$3$$ volt battery with negligible internal resistance is connected in a circuit as shown in the figure. The current $${\rm I}$$, in the circuit will be
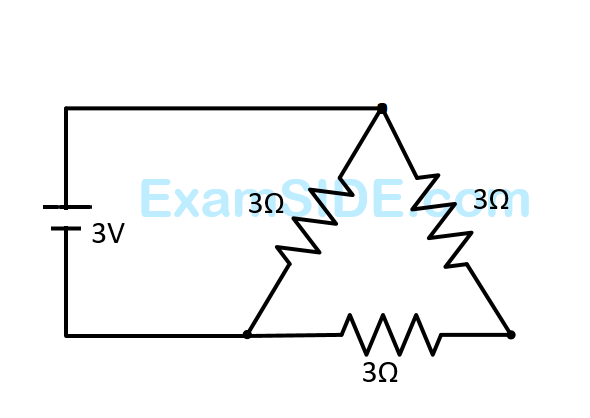

13
A $$220$$ volt, $$1000$$ watt bulb is connected across a $$110$$ $$volt$$ mains supply. The power consumed will be
14
A particle of mass $$M$$ and charge $$Q$$ moving with velocity $$\overrightarrow v $$ describe a circular path of radius $$R$$ when subjected to a uniform transverse magnetic field of induction $$B.$$ The network done by the field when the particle completes one full circle is
15
A particle of charge $$ - 16 \times {10^{ - 18}}$$ coulomb moving with velocity $$10m{s^{ - 1}}$$ along the $$x$$-axis enters a region where a magnetic field of induction $$B$$ is along the $$y$$-axis, and an electric field of magnitude $${10^4}V/m$$ is along the negative $$z$$-axis. If the charged particle continues moving along the $$x$$-axis, the magnitude of $$B$$ is
16
A magnetic needle lying parallel to a magnetic field requires $$W$$ units of work to turn it through $${60^ \circ }.$$ The torque needed to maintain the needle in this position will be :
17
The magnetic lines of force inside a bar magnet
18
Two coils are placed close to each other. The mutual inductance of the pair of coils depends upon
19
In an oscillating $$LC$$ circuit the maximum charge on the capacitor is $$Q$$. The charge on the capacitor when the energy is stored equally between the electric and magnetic field is
20
The core of any transformer is laminated so as to
21
To demonstrate the phenomenon of interference, we require two sources which emit radiation
22
The image formed by an objective of a compound microscope is
23
To get three images of a single object, one should have two plane mirrors at an angle of
24
A strip of copper and another of germanium are cooled from room temperature to $$80K.$$ The resistance of
25
The difference in the variation of resistance with temperature in a metal and a semiconductor arises essentially due to the difference in the
26
Three charges $$ - {q_1}, + {q_2}$$ and $$ - {q_3}$$ are placed as shown in the figure. The $$x$$-component of the force on $$ - {q_1}$$ is proportional to
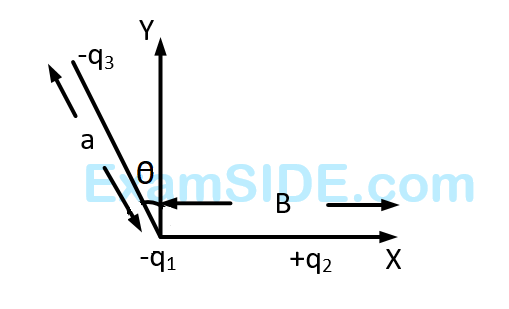

27
The earth radiates in the infra-red region of the spectrum. The spectrum is correctly given by
28
A particle performing uniform circular motion has angular frequency is doubled & its kinetic energy halved, then the new angular momentum is
29
Let $$\overrightarrow F $$ be the force acting on a particle having position vector $$\overrightarrow r ,$$ and $$\overrightarrow \tau $$ be the torque of this force about the origin. Then
30
A circular disc $$X$$ of radius $$R$$ is made from an iron plate of thickness $$t,$$ and another disc $$Y$$ of radius $$4$$ $$R$$ is made from an iron plate of thickness $${t \over 4}.$$ Then the relation between the moment of inertia $${I_X}$$ and $${I_Y}$$ is
31
The time period of satellite of earth is $$5$$ hours. If the separation between the earth and the satellite is increased to $$4$$ times the previous value, the new time period will become
32
Two spherical bodies of mass $$M$$ and $$5M$$ & radii $$R$$ & $$2R$$ respectively are released in free space with initial separation between their centers equal to $$12R$$. If they attract each other due to gravitational force only, then the distance covered by the smaller body just before collision is
33
The escape velocity for a body projected vertically upwards from the surface of earth is $$11$$ $$km/s.$$ If the body is projected at an angle of $${45^ \circ }$$ with the vertical, the escape velocity will be
34
Three forces start acting simultaneously on a particle moving with velocity, $$\overrightarrow v \,\,.$$ These forces are represented in magnitude and direction by the three sides of a triangle $$ABC$$. The particle will now move with velocity
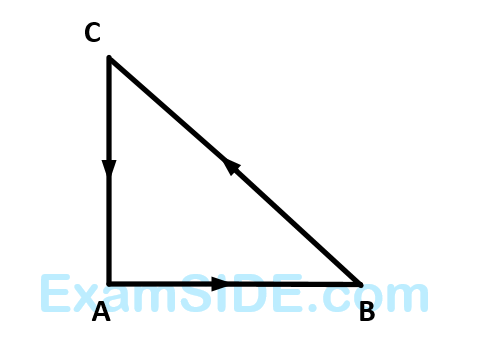

35
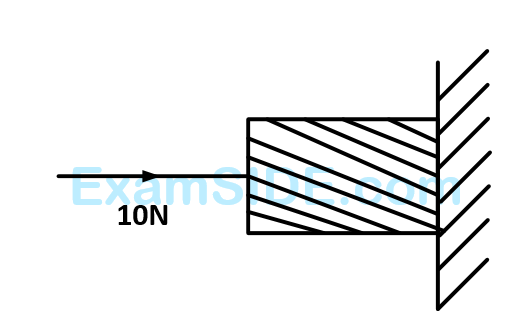
A horizontal force of $$10$$ $$N$$ is necessary to just hold a block stationary against a wall. The coefficient of friction between the block and the wall is $$0.2$$. The weight of the block is

36
''Heat cannot by itself flow from a body at lower temperature to a body at higher temperature'' is a statement or consequence of :
37
During an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio $${C_p}/{C_V}$$ for the gas is
38
Which of the following parameters does not characterize the thermodynamic state of mattter?
39
A body is moved along a straight line by a machine delivering a constant power. The distance moved by the body in time $$'t'$$ is proportional to
40
A mass $$M$$ is suspended from a spring of negligible mass. The spring is pulled a little and then released so that the mass executes $$SHM$$ of time period $$T.$$ If the mass is increased by $$m.$$ the time period becomes $${{5T} \over 3}$$. Then the ratio of $${{m} \over M}$$ is
41
Two particles $$A$$ and $$B$$ of equal masses are suspended from two massless springs of spring of spring constant $${k_1}$$ and $${k_2}$$, respectively. If the maximum velocities, during oscillation, are equal, the ratio of amplitude of $$A$$ and $$B$$ is
42
The length of a simple pendulum executing simple harmonic motion is increased by $$21\% $$. The percentage increase in the time period of the pendulum of increased length is
43
A body executes simple harmonic motion. The potential energy $$(P.E),$$ the kinetic energy $$(K.E)$$ and total energy $$(T.E)$$ are measured as a function of displacement $$x.$$ Which of the following statements is true ?
44
The displacement of particle varies according to the relation
$$x=4$$$$\left( {\cos \,\pi t + \sin \,\pi t} \right).$$ The amplitude of the particle is
$$x=4$$$$\left( {\cos \,\pi t + \sin \,\pi t} \right).$$ The amplitude of the particle is
45
A metal wire of linear mass density of $$9.8$$ $$g/m$$ is stretched with a tension of $$10$$ $$kg$$-$$wt$$ between two rigid supports $$1$$ metre apart. The wire passes at its middle point between the poles of a permanent magnet, and it vibrates in resonance when carrying an alternating current of frequency $$n.$$ The frequency $$n$$ of the alternating source is
46
The displacement $$y$$ of a wave travelling in the $$x$$-direction is given by
$$$y = {10^{ - 4}}\,\sin \left( {600t - 2x + {\pi \over 3}} \right)\,\,metres$$$
where $$x$$ is expressed in metres and $$t$$ in seconds. The speed of the wave - motion, in $$m{s^{ - 1}}$$, is
where $$x$$ is expressed in metres and $$t$$ in seconds. The speed of the wave - motion, in $$m{s^{ - 1}}$$, is
47
A tuning fork of known frequency $$256$$ $$Hz$$ makes $$5$$ beats per second with the vibrating string of a piano. The beat frequency decreases to $$2$$ beats per second when the tension in the piano string is slightly increased. The frequency of the piano string before increasing the tension was
48
A sheet of aluminium foil of negligible thickness is introduced between the plates of a capacitor. The capacitance of the capacitor
49
If the electric flux entering and leaving an enclosed surface respectively is $${\phi _1}$$ and $${\phi _2},$$ the electric charge inside the surface will be
50
A thin spherical conducting shell of radius $$R$$ has a charge $$q.$$ Another charge $$Q$$ is placed at the center of the shell. The electrostatic potential at a point $$P$$ a distance $${R \over 2}$$ from the center of the shell is
51
The work done in placing a charge of $$8 \times {10^{ - 18}}$$ coulomb on a condenser of capacity $$100$$ micro-farad is
52
Dimensions of $${1 \over {{\mu _0}{\varepsilon _0}}}$$, where symbols have their usual meaning, are
53
The physical quantities not having same dimensions are
54
A car, moving with a speed of 50 km/hr, can be stopped by brakes after at least 6 m. If the
same car is moving at a speed of 100 km/hr, the minimum stopping distance is
55
A boy playing on the roof of a 10 m high building throws a ball with a speed of 10 m/s at an
angle of $$30^\circ $$ with the horizontal. How far from the throwing point will the ball be at the height
of 10 m from the ground?
$$\left[ {g = 10m/{s^2},\sin 30^\circ = {1 \over 2},\cos 30^\circ = {{\sqrt 3 } \over 2}} \right]$$
56
The co-ordinates of a moving particle at any time 't' are given by x = $$\alpha $$t3 and y = βt3. The speed to the particle at time 't' is given by
57
A spring balance is attached to the ceiling of a lift. A man hangs his bag on the spring and the spring reads $$49$$ $$N,$$ when the lift is stationary. If the lift moves downward with an acceleration of $$5 m/{s^2}$$, the reading of the spring balance will be
58
A marble block of mass $$2$$ $$kg$$ lying on ice when given a velocity of $$6$$ $$m/s$$ is stopped by friction in $$10$$ $$s.$$ Then the coefficient of friction is
59
A block of mass $$M$$ is pulled along a horizontal frictionless surface by a rope of mass $$m.$$ If a force $$P$$ is applied at the free end of the rope, the force exerted by the rope on the block is
60
A light spring balance hangs from the hook of the other light spring balance and a block of mass $$M$$ $$kg$$ hangs from the former one. Then the true statement about the scale reading is
61
A rocket with a lift-off mass $$3.5 \times {10^4}\,\,kg$$ is blasted upwards with an initial acceleration of $$10m/{s^2}.$$ Then the initial thrust of the blast is
62
Consider the following two statements :
$$A.$$ Linear momentum of a system of particles is zero
$$B.$$ Kinetic energy of a system of particles is zero.
then
$$A.$$ Linear momentum of a system of particles is zero
$$B.$$ Kinetic energy of a system of particles is zero.
then
63
A wire suspended vertically from one of its ends is stretched by attaching a weight of $$200N$$ to the lower end. The weight stretches the wire by $$1$$ $$mm.$$ Then the elastic energy stored in the wire is
64
A spring of spring constant $$5 \times {10^3}\,N/m$$ is stretched initially by $$5$$ $$cm$$ from the unstretched position. Then the work required to stretch it further by another $$5$$ $$cm$$ is