JEE Main 2018 (Offline)
Paper was held on
Sun, Apr 15, 2018 10:00 AM
Chemistry
1
The increasing order of basicity of the following compounds is :


2
An alkali is titrated against an acid with methyl orange as indicator, which of the following is a correct combination?
3
The predominant form of histamine present in human blood is (pKa, Histidine = 6.0)
4
Glucose on prolonged heating with HI gives
5
The major product formed in the following reaction is :


6
Phenol reacts with methyl chloroformate in the presence of NaOH to form product A. A reacts with Br2 to
form product B. A and B are respectively :
7
Phenol on treatment with CO2 in the presence of NaOH followed by acidification produces compound X as
the major product. X on treatment with (CH3CO)2O in the presence of catalytic amount of H2SO4 produces:
8
The trans-alkenes are formed by the reduction of alkynes with
9
The major product of the following reaction is:


10
Which of the following compounds will be suitable for Kjeldahl’s method for nitrogen estimation?
11
The compound that does not produce nitrogen gas by the thermal decomposition is :
12
The oxidation states of Cr in [Cr(H2O)6]Cl3, [Cr(C6H6)2] and K2[Cr(CN)2(O)2(O2)(NH3)] respectively are :
13
Consider the following reaction and statements:
[Co(NH3)4Br2]+ + Br- $$\to$$ [Co(NH3)3Br3] + NH3
(I) Two isomers are produced if the reactant complex ion is a cis-isomer
(II) Two isomers are produced if the reactant complex ion is a trans-isomer
(III) Only one isomer is produced if the reactant complex ion is a trans-isomer
(IV) Only one isomer is produced if the reactant complex ion is a cis – isomer
The correct statements are
[Co(NH3)4Br2]+ + Br- $$\to$$ [Co(NH3)3Br3] + NH3
(I) Two isomers are produced if the reactant complex ion is a cis-isomer
(II) Two isomers are produced if the reactant complex ion is a trans-isomer
(III) Only one isomer is produced if the reactant complex ion is a trans-isomer
(IV) Only one isomer is produced if the reactant complex ion is a cis – isomer
The correct statements are
14
Which of the following compounds contain(s) no covalent bond(s)?
KCl, PH3, O2, B2H6, H2SO4
15
How long (approximate) should water be electrolysed by passing through 100 amperes current so that the
oxygen released can completely burn 27.66 g of diborane?
(Atomic weight of B = 10.8 u)
(Atomic weight of B = 10.8 u)
16
At 518oC the rate of decomposition of a sample of gaseous acetaldehyde initially at a pressure of 363 Torr,
was 1.00 Torr s–1 when 5% had reacted and 0.5 Torr s–1 when 33% had reacted. The order of the reaction is
17
Which of the following salts is the most basic in aqueous solution?
18
Which of the following are Lewis acids?
19
An aqueous solution contains 0.10 M H2S and 0.20 M HCl. If the equilibrium constants for the formation of HS– from H2S is 1.0 $$\times$$ 10–7 and that of S2- from HS– ions is 1.2 $$\times$$ 10–13 then the concentration of S2- ions in aqueous solution is :
20
An aqueous solution contains an unknown concentration of Ba2+. When 50 mL of a 1 M solution of Na2SO4 is added, BaSO4 just begins to precipitate. The final volume is 500 mL. The solubility product of BaSO4 is 1 $$\times$$ 10–10. What is the original concentration of Ba2+?
21
For 1 molal aqueous solution of the following compounds, which one will show the highest freezing
point?
22
Which of the following lines correctly show the temperature dependence of equilibrium constant K, for an
exothermic reaction?
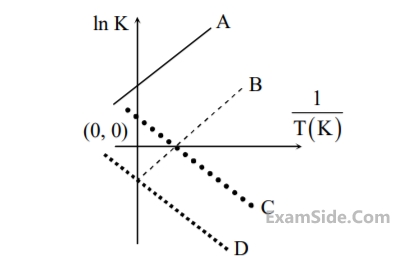

23
The combustion of benzene(l) gives CO2(g) and H2O(l). Given that heat of combustion of benzene at constant volume is –3263.9 kJ mol–1 at 25oC; heat of combustion (in kJ mol–1) of benzene at constant pressure will be :
(R = 8.314 JK–1 mol–1)
(R = 8.314 JK–1 mol–1)
24
Total number of lone pair of electrons in $${\rm I}_3^ - $$ ion is
25
According to molecular orbital theory, which of the following will not be a viable molecule?
26
The ratio of mass percent of C and H of an organic compound (CXHYOZ) is 6 : 1. If one molecule of the above compound (CXHYOZ) contains half as much oxygen as required to burn one molecule of compound CXHY completely to CO2 and H2O. The empirical formula of compound CXHYOZ is
Mathematics
1
From 6 different novels and 3 different dictionaries, 4 novels and 1 dictionary are to be selected and
arranged in a row on a shelf so that the dictionary is always in the middle. The number of such
arrangements is :
2
Let S = { $$x$$ $$ \in $$ R : $$x$$ $$ \ge $$ 0 and
$$2\left| {\sqrt x - 3} \right| + \sqrt x \left( {\sqrt x - 6} \right) + 6 = 0$$}. Then S
$$2\left| {\sqrt x - 3} \right| + \sqrt x \left( {\sqrt x - 6} \right) + 6 = 0$$}. Then S
3
If $$\alpha ,\beta \in C$$ are the distinct roots of the equation
x2 - x + 1 = 0, then $${\alpha ^{101}} + {\beta ^{107}}$$ is equal to :
x2 - x + 1 = 0, then $${\alpha ^{101}} + {\beta ^{107}}$$ is equal to :
4
If the system of linear equations
x + ky + 3z = 0
3x + ky - 2z = 0
2x + 4y - 3z = 0
has a non-zero solution (x, y, z), then $${{xz} \over {{y^2}}}$$ is equal to
x + ky + 3z = 0
3x + ky - 2z = 0
2x + 4y - 3z = 0
has a non-zero solution (x, y, z), then $${{xz} \over {{y^2}}}$$ is equal to
5
If $$\left| {\matrix{
{x - 4} & {2x} & {2x} \cr
{2x} & {x - 4} & {2x} \cr
{2x} & {2x} & {x - 4} \cr
} } \right| = \left( {A + Bx} \right){\left( {x - A} \right)^2}$$
then the ordered pair (A, B) is equal to :
then the ordered pair (A, B) is equal to :
6
Two sets A and B are as under :
A = {($$a$$, b) $$ \in $$ R $$ \times $$ R : |$$a$$ - 5| < 1 and |b - 5| < 1};
B = {($$a$$, b) $$ \in $$ R $$ \times $$ R : 4($$a$$ - 6)2 + 9(b - 5)2 $$ \le $$ 36 };
Then
A = {($$a$$, b) $$ \in $$ R $$ \times $$ R : |$$a$$ - 5| < 1 and |b - 5| < 1};
B = {($$a$$, b) $$ \in $$ R $$ \times $$ R : 4($$a$$ - 6)2 + 9(b - 5)2 $$ \le $$ 36 };
Then
7
Let $${a_1}$$, $${a_2}$$, $${a_3}$$, ......... ,$${a_{49}}$$ be in A.P. such that
$$\sum\limits_{k = 0}^{12} {{a_{4k + 1}}} = 416$$ and $${a_9} + {a_{43}} = 66$$.
$$a_1^2 + a_2^2 + ....... + a_{17}^2 = 140m$$, then m is equal to
$$\sum\limits_{k = 0}^{12} {{a_{4k + 1}}} = 416$$ and $${a_9} + {a_{43}} = 66$$.
$$a_1^2 + a_2^2 + ....... + a_{17}^2 = 140m$$, then m is equal to
8
A bag contains 4 red and 6 black balls. A ball is drawn at random from the bag, its colour is observed and
this ball along with two additional balls of the same colour are returned to the bag. If now a ball is drawn at
random from the bag, then the probability that this drawn ball is red, is :
9
If $$\sum\limits_{i = 1}^9 {\left( {{x_i} - 5} \right)} = 9$$ and
$$\sum\limits_{i = 1}^9 {{{\left( {{x_i} - 5} \right)}^2}} = 45$$, then the standard deviation of the 9 items
$${x_1},{x_2},.......,{x_9}$$ is
$$\sum\limits_{i = 1}^9 {{{\left( {{x_i} - 5} \right)}^2}} = 45$$, then the standard deviation of the 9 items
$${x_1},{x_2},.......,{x_9}$$ is
10
Let $$\overrightarrow u $$ be a vector coplanar with the vectors $$\overrightarrow a = 2\widehat i + 3\widehat j - \widehat k$$ and $$\overrightarrow b = \widehat j + \widehat k$$. If $$\overrightarrow u $$ is perpendicular to $$\overrightarrow a $$ and $$\overrightarrow u .\overrightarrow b = 24$$, then $${\left| {\overrightarrow u } \right|^2}$$ is equal to
11
A straight line through a fixed point (2, 3) intersects the coordinate axes at distinct points P and Q. If O is
the origin and the rectangle OPRQ is completed, then the locus of R is :
12
Let y = y(x) be the solution of the differential equation
$$\sin x{{dy} \over {dx}} + y\cos x = 4x$$, $$x \in \left( {0,\pi } \right)$$.
If $$y\left( {{\pi \over 2}} \right) = 0$$, then $$y\left( {{\pi \over 6}} \right)$$ is equal to :
$$\sin x{{dy} \over {dx}} + y\cos x = 4x$$, $$x \in \left( {0,\pi } \right)$$.
If $$y\left( {{\pi \over 2}} \right) = 0$$, then $$y\left( {{\pi \over 6}} \right)$$ is equal to :
13
The integral
$$\int {{{{{\sin }^2}x{{\cos }^2}x} \over {{{\left( {{{\sin }^5}x + {{\cos }^3}x{{\sin }^2}x + {{\sin }^3}x{{\cos }^2}x + {{\cos }^5}x} \right)}^2}}}} dx$$
is equal to
$$\int {{{{{\sin }^2}x{{\cos }^2}x} \over {{{\left( {{{\sin }^5}x + {{\cos }^3}x{{\sin }^2}x + {{\sin }^3}x{{\cos }^2}x + {{\cos }^5}x} \right)}^2}}}} dx$$
is equal to
14
The value of $$\int\limits_{ - \pi /2}^{\pi /2} {{{{{\sin }^2}x} \over {1 + {2^x}}}} dx$$ is
15
Let g(x) = cosx2, f(x) = $$\sqrt x $$ and $$\alpha ,\beta \left( {\alpha < \beta } \right)$$ be the roots of the quadratic equation 18x2 - 9$$\pi $$x + $${\pi ^2}$$ = 0. Then the area (in sq. units) bounded by the curve
y = (gof)(x) and the lines $$x = \alpha $$, $$x = \beta $$ and y = 0 is :
y = (gof)(x) and the lines $$x = \alpha $$, $$x = \beta $$ and y = 0 is :
16
Let S = { t $$ \in R:f(x) = \left| {x - \pi } \right|.\left( {{e^{\left| x \right|}} - 1} \right)$$$$\sin \left| x \right|$$ is not differentiable at t}, then the set S is equal to
17
Let $$f\left( x \right) = {x^2} + {1 \over {{x^2}}}$$ and $$g\left( x \right) = x - {1 \over x}$$,
$$x \in R - \left\{ { - 1,0,1} \right\}$$.
If $$h\left( x \right) = {{f\left( x \right)} \over {g\left( x \right)}}$$, then the local minimum value of h(x) is
$$x \in R - \left\{ { - 1,0,1} \right\}$$.
If $$h\left( x \right) = {{f\left( x \right)} \over {g\left( x \right)}}$$, then the local minimum value of h(x) is
18
For each t $$ \in R$$, let [t] be the greatest integer less than or equal to t.
Then $$\mathop {\lim }\limits_{x \to {0^ + }} x\left( {\left[ {{1 \over x}} \right] + \left[ {{2 \over x}} \right] + ..... + \left[ {{{15} \over x}} \right]} \right)$$
Then $$\mathop {\lim }\limits_{x \to {0^ + }} x\left( {\left[ {{1 \over x}} \right] + \left[ {{2 \over x}} \right] + ..... + \left[ {{{15} \over x}} \right]} \right)$$
Physics
1
A granite rod of 60 cm length is clamped at its middle point and is set into longitudinal vibrations. The
density of granite is 2.7 $$\times$$ 103 kg/m3 and its Young’s modulus is 9.27 $$\times$$ 1010 Pa. What will be the fundamental frequency of the longitudinal vibrations ?
2
The angular width of the central maximum in a single slit diffraction pattern is 60°. The width of the slit is
1 $$\mu $$m. The slit is illuminated by monochromatic plane waves. If another slit of same width is made near it,
Young’s fringes can be observed on a screen placed at a distance 50 cm from the slits. If the observed
fringe width is 1 cm, what is slit separation distance?
(i.e. distance between the centres of each slit.)
3
An EM wave from air enters a medium. The electric fields are
$$\overrightarrow {{E_1}} $$ = $${E_{01}}\widehat x\cos \left[ {2\pi v\left( {{z \over c} - t} \right)} \right]$$ in air and
$$\overrightarrow {{E_2}} $$ = $${E_{02}}\widehat x\cos \left[ {k\left( {2z - ct} \right)} \right]$$ in medium,
where the wave number k and frequency $$\nu $$ refer to their values in air. The medium is non-magnetic. If $${\varepsilon _{{r_1}}}$$ and $${\varepsilon _{{r_2}}}$$ refer to relative permittivities of air and medium respectively, which of the following options is correct ?
$$\overrightarrow {{E_1}} $$ = $${E_{01}}\widehat x\cos \left[ {2\pi v\left( {{z \over c} - t} \right)} \right]$$ in air and
$$\overrightarrow {{E_2}} $$ = $${E_{02}}\widehat x\cos \left[ {k\left( {2z - ct} \right)} \right]$$ in medium,
where the wave number k and frequency $$\nu $$ refer to their values in air. The medium is non-magnetic. If $${\varepsilon _{{r_1}}}$$ and $${\varepsilon _{{r_2}}}$$ refer to relative permittivities of air and medium respectively, which of the following options is correct ?
4
In an a.c. circuit, the instantaneous e.m.f. and current are given by
e = 100 sin 30 t
i = 20 sin $$\left( {30t - {\pi \over 4}} \right)$$
In one cycle of a.c., the average power consumed by the circuit and the wattless current are, respectively
e = 100 sin 30 t
i = 20 sin $$\left( {30t - {\pi \over 4}} \right)$$
In one cycle of a.c., the average power consumed by the circuit and the wattless current are, respectively
5
The dipole moment of a circular loop carrying a current I, is m and the magnetic field at the centre of the
loop is B1. When the dipole moment is doubled by keeping the current constant, the magnetic field at the
centre of the loop is $${{B_2}}$$. The ratio $${{{B_1}} \over {{B_2}}}$$ is:
6
An electron, a proton and an alpha particle having the same kinetic energy are moving in circular orbits of
radii re, rp, r$$_\alpha$$ respectively in a uniform magnetic field B. The relation between re, rp, r$$_\alpha$$ is:
7
On interchanging the resistances, the balance point of a meter bridge shifts to the left by 10 cm. The
resistance of their series combination is 1 k$$\Omega $$. How much was the resistance on the left slot before
interchanging the resistances?
8
Two batteries with e.m.f 12 V and 13 V are connected in parallel across a load resistor of 10 $$\Omega $$. The
internal resistances of the two batteries are 1 $$\Omega $$ and 2 $$\Omega $$ respectively. The voltage across the load lies between :
9
Three concentric metal shells A, B and C of respective radii a, b and c (a < b < c) have surface charge
densities $$ + \sigma $$, $$ - \sigma $$ and $$ + \sigma $$ respectively. The potential of shell B is :
10
A parallel plate capacitor of capacitance 90 pF is connected to a battery of emf 20 V. If a dielectric material
of dielectric constant K = 5/3 is inserted between the plates, the magnitude of the induced charge will be :
11
A silver atom in a solid oscillates in simple harmonic motion in some direction with a frequency of 1012/sec. What is the force constant of the bonds connecting one atom with the other? (Mole wt. of silver = 108 and Avogadro number = 6.02 × 1023 gm mole–1)
12
Unpolarized light of intensity I passes through an ideal polarizer A. Another identical polarizer B is placed
behind A. The intensity of light beyond B is found to be I/2. Now another identical polarizer C is placed between A and B. The intensity beyond B is now found to be I/8. The angle between polarizer A and C is :
13
The mass of a hydrogen molecule is 3.32 $$\times$$ 10-27 kg. If 1023 hydrogen molecules strike, per second, a fixed wall of area 2 cm2 at an angle of 45o to the normal, and rebound elastically with a speed of 103 m/s, then the pressure on the wall is nearly:
14
Two moles of an ideal monatomic gas occupies a volume V at 27oC. The gas expands adiabatically to a
volume 2 V. Calculate (a) the final temperature of the gas and (b) change in its internal energy.
15
A particle is moving with a uniform speed in a circular orbit of radius R in a central force inversely
proportional to the nth power of R. If the period of rotation of the particle is T, then :
16
From a uniform circular disc of radius R and mass 9M, a small disc
of radius R/3 is removed as shown in the figure. The moment of
inertia of the remaining disc about an axis perpendicular to the plane
of the disc and passing through centre of disc is :
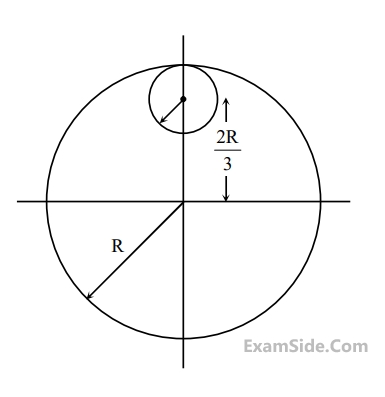

17
A particle is moving in a circular path of radius $$a$$ under the action of an attractive potential $$U = - {k \over {2{r^2}}}$$ Its total energy is:
18
A solid sphere of radius r made of a soft material of bulk modulus K is surrounded by a liquid in a
cylindrical container. A massless piston of area a floats on the surface of the liquid, covering entire cross
section of cylindrical container. When a mass m is placed on the surface of the piston to compress the
liquid, the fractional decrement in the radius of the sphere, $$\left( {{dr \over r}} \right)$$ is:
19
Seven identical circular planar disks, each of mass M and radius R are
welded symmetrically as shown. The moment of inertia of the arrangement
about the axis normal to the plane and passing through the point P is :
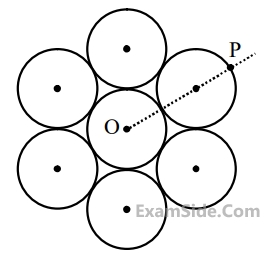

20
In a collinear collision, a particle with an initial speed v0 strikes a stationary particle of the same mass. If
the final total kinetic energy is 50% greater than the original kinetic energy, the magnitude of the relative
velocity between the two particles, after collision, is :
21
Two masses m1 = 5 kg and m2 = 10 kg, connected by an inextensible
string over a frictionless pulley, are moving as shown in the figure. The
coefficient of friction of horizontal surface is 0.15. The minimum
weight m that should be put on top of m2 to stop the motion is :
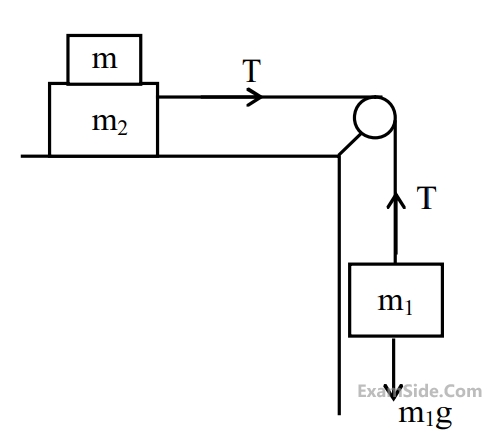

22
All the graphs below are intended to represent the same motion. One of them does it incorrectly. Pick it up.
23
The density of a material in the shape of a cube is determined by measuring three sides of the cube and its
mass. If the relative errors in measuring the mass and length are respectively 1.5% and 1%, the maximum
error in determining the density is:
24
The reading of the ammeter for a silicon diode in the given circuit
is :


25
If the series limit frequency of the Lyman series is $${\nu _L}$$, then the series limit frequency of the Pfund series is:
26
It is found that if a neutron suffers an elastic collinear collision with deuterium at rest, fractional loss of its
energy is pd; while for its similar collision with carbon nucleus at rest, fractional loss of energy is pc. The values of pd and pc are respectively :
27
An electron from various excited states of hydrogen atom emit radiation to come to the ground state. Let
$${\lambda _n}$$, $${\lambda _g}$$ be the de Broglie wavelength of the electron in the nth state and the ground state respectively. Let
$${\Lambda _n}$$ be the wavelength of the emitted photon in the transition from the nth state to the ground state. For large n, (A, B are constants)