JEE Main 2021 (Online) 20th July Evening Shift
Paper was held on
Tue, Jul 20, 2021 9:30 AM
Chemistry
1
Which one of the following pairs of isomers is an example of metamerism?
2

In the above reactions, product A and product B respectively are :
3
The major product (P) in the following reaction is :


4
A solution is 0.1 M in Cl$$-$$ and 0.001 M in CrO$$_4^{2 - }$$. Solid AgNO3 is gradually added to it. Assuming that the addition does not change in volume and Ksp(AgCl) = 1.7 $$\times$$ 10$$-$$10 M2 and Ksp(Ag2CrO4) = 1.9 $$\times$$ 10$$-$$12 M3.
Select correct statement from the following :
Select correct statement from the following :
5
Outermost electronic configuration of a group 13 element, E, is 4s2, 4p1. The electronic configuration of an element of p-block period-five placed diagonally to element, E is :
6
Metallic sodium does not react normally with :
7
Spin only magnetic moment of an octahedral complex of Fe2+ in the presence of a strong field ligand in BM is :
8
Which one of the following species doesn't have a magnetic moment of 1.73 BM, (spin only value)?
9
Which one of the following statements is not true about enzymes?
10
The hybridisations of the atomic orbitals of nitrogen in NO$$_2^ - $$, NO$$_2^ + $$ and NH$$_4^ + $$ respectively are.
11
Benzene on nitration gives nitrobenzene in presence of HNO3 and H2SO4 mixture, where :
12

Consider the above reaction, compound B is :
13

Major product P of above reaction, is :
14
Cu2+ salt reacts with potassium iodide to give
15
In Carius method, halogen containing organic compound is heated with fuming nitric acid in the presence of :
16

The correct order of their reactivity towards hydrolysis at room temperature is :
17
For a given chemical reaction A $$\to$$ B at 300 K the free energy change is $$-$$49.4 kJ mol$$-$$1 and the enthalpy of reaction is 51.4 kJ mol$$-$$1. The entropy change of the reaction is _____________ JK$$-$$1 mol$$-$$1.
18
The wavelength of electrons accelerated from rest through a potential difference of 40 kV is x $$\times$$ 10$$-$$12 m. The value of x is ___________. (Nearest integer)
Give : Mass of electron = 9.1 $$\times$$ 10$$-$$31 kg
Charge on an electron = 1.6 $$\times$$ 10$$-$$19 C
Planck's constant = 6.63 $$\times$$ 10$$-$$34 Js
Give : Mass of electron = 9.1 $$\times$$ 10$$-$$31 kg
Charge on an electron = 1.6 $$\times$$ 10$$-$$19 C
Planck's constant = 6.63 $$\times$$ 10$$-$$34 Js
19
The vapour pressures of A and B at 25$$^\circ$$C are 90 mm Hg and 15 mm Hg respectively. If A and B are mixed such that the mole fraction of A in the mixture is 0.6, then the mole fraction of B in the vapour phase is x $$\times$$ 10$$-$$1. The value of x is ___________. (Nearest integer)
20
4g equimolar mixture of NaOH and Na2CO3 contains x g of NaOH and y g of Na2CO3. The value of x is ____________ g. (Nearest integer)
21
When 0.15 g of an organic compound was analyzed using Carius method for estimation of bromine, 0.2397 g of AgBr was obtained. The percentage of bromine in the organic compound is ______________. (Nearest integer)
[Atomic mass : Silver = 108, Bromine = 80]
[Atomic mass : Silver = 108, Bromine = 80]
22
$$PC{l_5}(g) \to PC{l_3}(g) + C{l_2}(g)$$
In the above first order reaction the concentration of PCl5 reduces from initial concentration 50 mol L$$-$$1 to 10 mol L$$-$$1 in 120 minutes at 300 K. The rate constant for the reaction at 300 K is x $$\times$$ 10$$-$$2 min$$-$$1. The value of x is __________. [Given log5 = 0.6989]
In the above first order reaction the concentration of PCl5 reduces from initial concentration 50 mol L$$-$$1 to 10 mol L$$-$$1 in 120 minutes at 300 K. The rate constant for the reaction at 300 K is x $$\times$$ 10$$-$$2 min$$-$$1. The value of x is __________. [Given log5 = 0.6989]
23
An aqueous solution of NiCl2 was heated with excess sodium cyanide in presence of strong oxidizing agent to form [Ni(CN)6]2$$-$$. The total change in number of unpaired electrons on metal centre is _______________.
24
Potassium chlorate is prepared by electrolysis of KCl in basic solution as shown by following equation.
6OH$$-$$ + Cl$$-$$ $$\to$$ ClO3$$-$$ + 3H2O + 6e$$-$$
A current of xA has to be passed for 10h to produce 10.0g of potassium chlorate. The value of x is ____________. (Nearest integer)
(Molar mass of KClO3 = 122.6 g mol$$-$$1, F = 96500 C)
6OH$$-$$ + Cl$$-$$ $$\to$$ ClO3$$-$$ + 3H2O + 6e$$-$$
A current of xA has to be passed for 10h to produce 10.0g of potassium chlorate. The value of x is ____________. (Nearest integer)
(Molar mass of KClO3 = 122.6 g mol$$-$$1, F = 96500 C)
Mathematics
1
The value of $$\tan \left( {2{{\tan }^{ - 1}}\left( {{3 \over 5}} \right) + {{\sin }^{ - 1}}\left( {{5 \over {13}}} \right)} \right)$$ is equal to :
2
The lines x = ay $$-$$ 1 = z $$-$$ 2 and x = 3y $$-$$ 2 = bz $$-$$ 2, (ab $$\ne$$ 0) are coplanar, if :
3
If [x] denotes the greatest integer less than or equal to x, then the value of the integral $$\int_{ - \pi /2}^{\pi /2} {[[x] - \sin x]dx} $$ is equal to :
4
If the real part of the complex number $${(1 - \cos \theta + 2i\sin \theta )^{ - 1}}$$ is $${1 \over 5}$$ for $$\theta \in (0,\pi )$$, then the value of the integral $$\int_0^\theta {\sin x} dx$$ is equal to:
5
Let $$f:R - \left\{ {{\alpha \over 6}} \right\} \to R$$ be defined by $$f(x) = {{5x + 3} \over {6x - \alpha }}$$. Then the value of $$\alpha$$ for which (fof)(x) = x, for all $$x \in R - \left\{ {{\alpha \over 6}} \right\}$$, is :
6
If $$f:R \to R$$ is given by $$f(x) = x + 1$$, then the value of $$\mathop {\lim }\limits_{n \to \infty } {1 \over n}\left[ {f(0) + f\left( {{5 \over n}} \right) + f\left( {{{10} \over n}} \right) + ...... + f\left( {{{5(n - 1)} \over n}} \right)} \right]$$ is :
7
Let A, B and C be three events such that the probability that exactly one of A and B occurs is (1 $$-$$ k), the probability that exactly one of B and C occurs is (1 $$-$$ 2k), the probability that exactly one of C and A occurs is (1 $$-$$ k) and the probability of all A, B and C occur simultaneously is k2, where 0 < k < 1. Then the probability that at least one of A, B and C occur is :
8
The sum of all the local minimum values of the twice differentiable function f : R $$\to$$ R defined by $$f(x) = {x^3} - 3{x^2} - {{3f''(2)} \over 2}x + f''(1)$$ is :
9
Let y = y(x) satisfies the equation $${{dy} \over {dx}} - |A| = 0$$, for all x > 0, where $$A = \left[ {\matrix{
y & {\sin x} & 1 \cr
0 & { - 1} & 1 \cr
2 & 0 & {{1 \over x}} \cr
} } \right]$$. If $$y(\pi ) = \pi + 2$$, then the value of $$y\left( {{\pi \over 2}} \right)$$ is :
10
If the mean and variance of six observations 7, 10, 11, 15, a, b are 10 and $${{20} \over 3}$$, respectively, then the value of | a $$-$$ b | is equal to :
11
Let $$g(t) = \int_{ - \pi /2}^{\pi /2} {\cos \left( {{\pi \over 4}t + f(x)} \right)} dx$$, where $$f(x) = {\log _e}\left( {x + \sqrt {{x^2} + 1} } \right),x \in R$$. Then which one of the following is correct?
12
Let P be a variable point on the parabola $$y = 4{x^2} + 1$$. Then, the locus of the mid-point of the point P and the foot of the perpendicular drawn from the point P to the line y = x is :
13
The value of k $$\in$$R, for which the following system of linear equations
3x $$-$$ y + 4z = 3,
x + 2y $$-$$ 3z = $$-$$2
6x + 5y + kz = $$-$$3,
has infinitely many solutions, is :
3x $$-$$ y + 4z = 3,
x + 2y $$-$$ 3z = $$-$$2
6x + 5y + kz = $$-$$3,
has infinitely many solutions, is :
14
In a triangle ABC, if $$\left| {\overrightarrow {BC} } \right| = 3$$, $$\left| {\overrightarrow {CA} } \right| = 5$$ and $$\left| {\overrightarrow {BA} } \right| = 7$$, then the projection of the vector $$\overrightarrow {BA} $$ on $$\overrightarrow {BC} $$ is equal to :
15
The number of solutions of the equation
$${\log _{(x + 1)}}(2{x^2} + 7x + 5) + {\log _{(2x + 5)}}{(x + 1)^2} - 4 = 0$$, x > 0, is :
$${\log _{(x + 1)}}(2{x^2} + 7x + 5) + {\log _{(2x + 5)}}{(x + 1)^2} - 4 = 0$$, x > 0, is :
16
Let a curve y = y(x) be given by the solution of the differential equation $$\cos \left( {{1 \over 2}{{\cos }^{ - 1}}({e^{ - x}})} \right)dx = \sqrt {{e^{2x}} - 1} dy$$. If it intersects y-axis at y = $$-$$1, and the intersection point of the curve with x-axis is ($$\alpha$$, 0), then e$$\alpha$$ is equal to __________________.
17
For p > 0, a vector $${\overrightarrow v _2} = 2\widehat i + (p + 1)\widehat j$$ is obtained by rotating the vector $${\overrightarrow v _1} = \sqrt 3 p\widehat i + \widehat j$$ by an angle $$\theta$$ about origin in counter clockwise direction. If $$\tan \theta = {{\left( {\alpha \sqrt 3 - 2} \right)} \over {\left( {4\sqrt 3 + 3} \right)}}$$, then the value of $$\alpha$$ is equal to _____________.
18
Consider a triangle having vertices A($$-$$2, 3), B(1, 9) and C(3, 8). If a line L passing through the circum-centre of triangle ABC, bisects line BC, and intersects y-axis at point $$\left( {0,{\alpha \over 2}} \right)$$, then the value of real number $$\alpha$$ is ________________.
19
If the point on the curve y2 = 6x, nearest to the point $$\left( {3,{3 \over 2}} \right)$$ is ($$\alpha$$, $$\beta$$), then 2($$\alpha$$ + $$\beta$$) is equal to _____________.
20
Let a function g : [ 0, 4 ] $$\to$$ R be defined as
$$g(x) = \left\{ {\matrix{ {\mathop {\max }\limits_{0 \le t \le x} \{ {t^3} - 6{t^2} + 9t - 3),} & {0 \le x \le 3} \cr {4 - x,} & {3 < x \le 4} \cr } } \right.$$, then the number of points in the interval (0, 4) where g(x) is NOT differentiable, is ____________.
$$g(x) = \left\{ {\matrix{ {\mathop {\max }\limits_{0 \le t \le x} \{ {t^3} - 6{t^2} + 9t - 3),} & {0 \le x \le 3} \cr {4 - x,} & {3 < x \le 4} \cr } } \right.$$, then the number of points in the interval (0, 4) where g(x) is NOT differentiable, is ____________.
21
If $$\mathop {\lim }\limits_{x \to 0} {{\alpha x{e^x} - \beta {{\log }_e}(1 + x) + \gamma {x^2}{e^{ - x}}} \over {x{{\sin }^2}x}} = 10,\alpha ,\beta ,\gamma \in R$$, then the value of $$\alpha$$ + $$\beta$$ + $$\gamma$$ is _____________.
Physics
1
If the Kinetic energy of a moving body becomes four times its initial Kinetic energy, then the percentage change in its momentum will be :
2
A boy reaches the airport and finds that the escalator is not working. He walks up the stationary escalator in time t1. If he remains stationary on a moving escalator then the escalator takes him up in time t2. The time taken by him to walk up on the moving escalator will be :
3
A satellite is launched into a circular orbit of radius R around earth, while a second satellite is launched into a circular orbit of radius 1.02 R. The percentage difference in the time periods of the two satellites is :
4
With what speed should a galaxy move outward with respect to earth so that the sodium-D line at wavelength 5890 $$\mathop A\limits^o $$ is observed at 5896 $$\mathop A\limits^o $$ ?
5
The length of a metal wire is l1, when the tension in it is T1 and is l2 when the tension is T2. The natural length of the wire is :
6
In an electromagnetic wave the electric field vector and magnetic field vector are given as $$\overrightarrow E = {E_0}\widehat i$$ and $$\overrightarrow B = {B_0}\widehat k$$ respectively. The direction of propagation of electromagnetic wave is along :
7
For a series LCR circuit with R = 100 $$\Omega$$, L = 0.5 mH and C = 0.1 pF connected across 220V$$-$$50 Hz AC supply, the phase angle between current and supplied voltage and the nature of the circuit is :
8
Which of the following graphs represent the behavior of an ideal gas? Symbols have their usual meaning.
9
A particle is making simple harmonic motion along the X-axis. If at a distances x1 and x2 from the mean position the velocities of the particle are v1 and v2 respectively. The time period of its oscillation is given as :
10
An electron having de-Broglie wavelength $$\lambda$$ is incident on a target in a X-ray tube. Cut-off wavelength of emitted X-ray is :
11
A body rolls down an inclined plane without slipping. The kinetic energy of rotation is 50% of its translational kinetic energy. The body is :
12
If time (t), velocity (v), and angular momentum (l) are taken as the fundamental units. Then the dimension of mass (m) in terms of t, v and l is :
13
The correct relation between the degrees of freedom f and the ratio of specific heat $$\gamma$$ is :
14
Consider a binary star system of star A and star B with masses mA and mB revolving in a circular orbit of radii rA an rB, respectively. If TA and TB are the time period of star A and star B, respectively,
Then :
Then :
15
A body at rest is moved along a horizontal straight line by a machine delivering a constant power. The distance moved by the body in time 't' is proportional to :
16
Two vectors $${\overrightarrow P }$$ and $${\overrightarrow Q }$$ have equal magnitudes. If the magnitude of $${\overrightarrow P + \overrightarrow Q }$$ is n times the magnitude of $${\overrightarrow P - \overrightarrow Q }$$, then angle between $${\overrightarrow P }$$ and $${\overrightarrow Q }$$ is :
17
Two small drops of mercury each of radius R coalesce to form a single large drop. The ratio of total surface energy before and after the change is :
18
The magnetic susceptibility of a material of a rod is 499. Permeability in vacuum is 4$$\pi$$ $$\times$$ 10$$-$$7 H/m. Absolute permeability of the material of the rod is :
19
A zener diode having zener voltage 8 V and power dissipation rating of 0.5 W is connected across a potential divider arranged with maximum potential drop across zener diode is as shown in the diagram. The value of protective resistance Rp is .................... $$\Omega$$.


20
A body of mass 'm' is launched up on a rough inclined plane making an angle of 30$$^\circ$$ with the horizontal. The coefficient of friction between the body and plane is $${{\sqrt x } \over 5}$$ if the time of ascent is half of the time of descent. The value of x is __________.
21
In the given figure switches S1 and S2 are in open condition. The resistance across ab when the switches S1 and S2 are closed is _____________ $$\Omega$$.


22
Two bodies, a ring and a solid cylinder of same material are rolling down without slipping an inclined plane. The radii of the bodies are same. The ratio of velocity of the centre of mass at the bottom of the inclined plane of the ring to that of the cylinder is $${{\sqrt x } \over 2}$$. Then, the value of x is _____________.
23
For the forward biased diode characteristics shown in the figure, the dynamic resistance at ID = 3 mA will be __________ $$\Omega$$.


24
A series LCR circuit of R = 5$$\Omega$$, L = 20 mH and C = 0.5 $$\mu$$F is connected across an AC supply of 250 V, having variable frequency. The power dissipated at resonance condition is ______________ $$\times$$ 102 W.
25
One mole of an ideal gas at 27$$^\circ$$ is taken from A to B as shown in the given PV indicator diagram. The work done by the system will be _________ $$\times$$ 10$$-$$1 J. [Given : R = 8.3 J/mole K, ln2 = 0.6931] (Round off to the nearest integer)
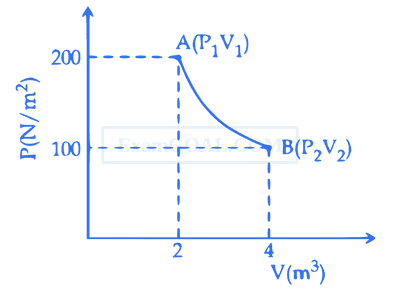

26
A certain metallic surface is illuminated by monochromatic radiation of wavelength $$\lambda$$. The stopping potential for photoelectric current for this radiation is 3V0. If the same surface is illuminated with a radiation of wavelength 2$$\lambda$$, the stopping potential is V0. The threshold wavelength of this surface for photoelectric effect is ____________ $$\lambda$$.
27
A body rotating with an angular speed of 600 rpm is uniformly accelerated to 1800 rpm in 10 sec. The number of rotations made in the process is ___________.