One mole of a symmetrical alkene on ozonolysis gives two moles of an aldehyde having a molecular mass of 44 u. The alkene is

The correct order of increasing basicity of the given conjugate bases (R = CH₃) is

Out of the following, the alkene that exhibits optical isomerism is

Solubility product of silver bromide is 5.0 $$\times$$ 10^–13. The quantity of potassium bromide (molar mass taken as 120g of mol^–1) to be added to 1 litre of 0.05 M solution of silver nitrate to start the precipitation of AgBr is :

In aqueous solution the ionization constants for carbonic acid are
K₁ = 4.2 x 10^–7 and K₂ = 4.8 x 10^–11
Select the correct statement for a saturated 0.034 M solution of the carbonic acid.

At 25°C, the solubility product of Mg(OH)₂ is 1.0 $$\times$$ 10^–11. At which pH, will Mg²⁺ ions start precipitating in the form of Mg(OH)₂ from a solution of 0.001 M Mg²⁺ ions?

Three reactions involving $$H_2PO_4^−$$ are given below :

(i) H₃PO₄ + H₂O $$\to$$ H₃O⁺ + $$H_2PO_4^−$$

(ii) $$H_2PO_4^−$$ + H₂O $$\to$$ $$HPO_4^{2−}$$ + H₃O⁺

(iii) $$H_2PO_4^−$$ + OH^- $$\to$$H₃PO₄ + O^2-

In which of the above does $$H_2PO_4^−$$ act as an acid?

For a particular reversible reaction at temperature T, ∆H and ∆S were found to be both +ve. If T_e is the temperature at equilibrium, the reaction would be spontaneous when :

The standard enthalpy of formation of NH₃ is –46.0 kJ mol^–1. If the enthalpy of formation of H₂ from its atoms is –436 kJ mol^–1 and that of N2 is –712 kJ mol^–1, the average bond enthalpy of N–H bond in NH₃ is :

Biuret test is not given by

In the chemical reactions,



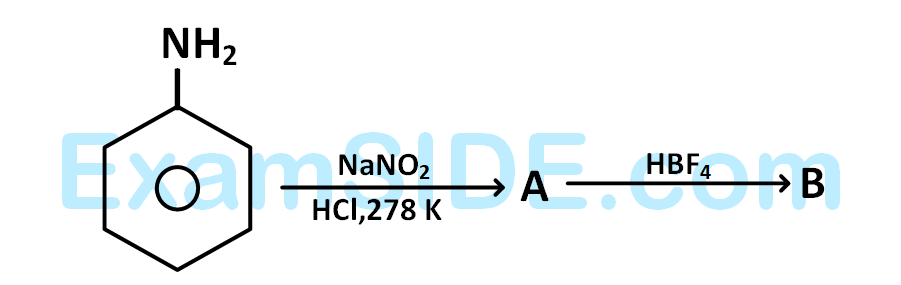
the compounds $$'A'$$ and $$'B'$$ respectively are

The main product of the following reaction is

$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $${C_6}{H_5}C{H_2}CH\left( {OH} \right)CH{\left( {C{H_3}} \right)_2}\buildrel {conc.{H_2}S{O_4}} \over \longrightarrow \,?$$

Consider the following bromides :



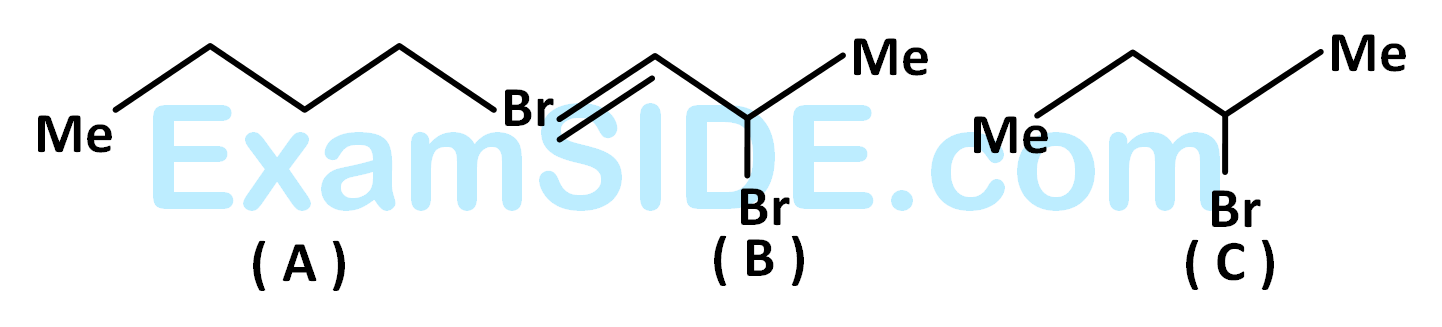
The correct order of $${S_N}1$$ reactive is

From amongst the following alcohols the one that would react fastest with conc. HCl and anhydrous ZnCl₂, is

A solution containing 2.675g of CoCl₃. 6NH₃ (molar mass = 267.5 g mol^–1) is passed through a cation exchanger. The chloride ions obtained in solution were treated with excess of AgNO₃ to give 4.78 g of AgCl (molar mass = 143.5 g mol^–1). The formula of the complex is : (At. Mass of Ag = 108 u)

Which one of the following has an optical isomer ?
(en = ethylenediamine)

29.5 mg of an organic compound containing nitrogen was digested according to Kjeldahl’s method and the evolved ammonia was absorbed in 20 mL of 0.1 M HCl solution. The excess of the acid required 15 mL of 0.1 M NaOH solution for complete neutralization. The percentage of nitrogen in the compound is

The time for half life period of a certain reaction A $$\to$$ products is 1 hour. When the initial concentration of the reactant ‘A’, is 2.0 mol L^–1, how much time does it take for its concentration to come from 0.50 to 0.25 mol L^–1 if it is a zero order reaction ?

Consider the reaction :

Cl₂(aq) + H₂S(aq) → S(s) + 2H⁺ (aq) + 2Cl^– (aq)

The rate equation for this reaction is rate = k [Cl₂] [H₂S]

Which of these mechanisms is/are consistent with this rate equation?

(A) Cl₂ + H₂S $$\to$$ H⁺ + Cl^– + Cl⁺ + HS^– (slow)

Cl⁺ + HS^– $$\to$$ H⁺ + Cl^– + S (fast)

(B) H₂S $$ \Leftrightarrow $$ H⁺ + HS^– (fast equilibrium)

Cl₂ + HS^– $$\to$$ 2Cl^– + H⁺ + S (slow)

The Gibbs energy for the decomposition of Al₂O₃ at 500^oC is as follows :

$${2 \over 3}A{l_2}{O_3}$$ $$\to$$ $${4 \over 3}Al + {O_2}$$, $${\Delta _r}G$$ = + 966 kJ mol^–1

The potential difference needed for electrolytic reduction of Al₂O₃ at 500^oC is at least :

The correct order of $$E_{{M^{2 + }}/M}^o$$ values with negative sign for the four successive elements Cr, Mn, Fe and Co is :

On mixing, heptane and octane form an ideal solution. At 373 K, the vapour pressures of the two liquid components (heptane and octane) are 105 kPa and 45 kPa respectively. Vapour pressure of the solution obtained by mixing 25.0g of heptane and 35 g of octane will be (molar mass of heptane = 100 g mol^–1 and of octane = 114 g mol^–1)

If sodium sulphate is considered to be completely dissociated into cations and anions in aqueous solution, the change in freezing point of water (∆T_f), when 0.01 mol of sodium sulphate is dissolved in 1 kg of water, is (K_f = 1.86 K kg mol^–1)

The correct sequence which shows decreasing order of the ionic radii of the elements is

Ionisation energy of He⁺ is 19.6 x 10^–18 J atom^–1. The energy of the first stationary state (n = 1) of Li²⁺ is

The energy required to break one mole of Cl–Cl bonds in Cl₂ is 242 kJ mol^–1. The longest wavelength of light capable of breaking a single Cl – Cl bond is
(c = 3 x 10⁸ ms^–1 and N_A = 6.02 x 10²³ mol^–1)

For two data sets, each of size 5, the variances are given to be 4 and 5 and the corresponding means are given to be 2 and 4, respectively. The variance of the combined data set is

Let $$f:R \to R$$ be a positive increasing function with

$$\mathop {\lim }\limits_{x \to \infty } {{f(3x)} \over {f(x)}} = 1$$. Then $$\mathop {\lim }\limits_{x \to \infty } {{f(2x)} \over {f(x)}} = $$

The number of complex numbers z such that $$\left| {z - 1} \right| = \left| {z + 1} \right| = \left| {z - i} \right|$$ equals :

Let $$f:R \to R$$ be defined by $$$f\left( x \right) = \left\{ {\matrix{ {k - 2x,\,\,if} & {x \le - 1} \cr {2x + 3,\,\,if} & {x > - 1} \cr } } \right.$$$

If $$f$$has a local minimum at $$x=-1$$, then a possible value of $$k$$ is

An urn contains nine balls of which three are red, four are blue and two are green. Three balls are drawn at random without replacement from the urn. The probability that the three balls have different colours is :

Four numbers are chosen at random (without replacement) from the set $$\left\{ {1,2,3,....20} \right\}.$$

Statement - 1: The probability that the chosen numbers when arranged in some order will form an AP is $${1 \over {85}}.$$

Statement - 2: If the four chosen numbers form an AP, then the set of all possible values of common difference is $$\left( { \pm 1, \pm 2, \pm 3, \pm 4, \pm 5} \right).$$

Solution of the differential equation

$$\cos x\,dy = y\left( {\sin x - y} \right)dx,\,\,0 < x <{\pi \over 2}$$ is :

Let $$p(x)$$ be a function defined on $$R$$ such that $$p'(x)=p'(1-x),$$ for all $$x \in \left[ {0,1} \right],p\left( 0 \right) = 1$$ and $$p(1)=41.$$ Then $$\int\limits_0^1 {p\left( x \right)dx} $$ equals :

The area bounded by the curves $$y = \cos x$$ and $$y = \sin x$$ between the ordinates $$x=0$$ and $$x = {{3\pi } \over 2}$$ is

The number of $$3 \times 3$$ non-singular matrices, with four entries as $$1$$ and all other entries as $$0$$, is :

Consider the system of linear equations; $$$\matrix{ {{x_1} + 2{x_2} + {x_3} = 3} \cr {2{x_1} + 3{x_2} + {x_3} = 3} \cr {3{x_1} + 5{x_2} + 2{x_3} = 1} \cr } $$$
The system has :

Let $$A$$ be a $$\,2 \times 2$$ matrix with non-zero entries and let $${A^2} = I,$$
where $$I$$ is $$2 \times 2$$ identity matrix. Define
$$Tr$$$$(A)=$$ sum of diagonal elements of $$A$$ and $$\left| A \right| = $$ determinant of matrix $$A$$.
Statement- 1: $$Tr$$$$(A)=0$$.
Statement- 2: $$\left| A \right| = 1$$ .

Let $$f:R \to R$$ be a continuous function defined by $$$f\left( x \right) = {1 \over {{e^x} + 2{e^{ - x}}}}$$$

Statement - 1 : $$f\left( c \right) = {1 \over 3},$$ for some $$c \in R$$.

Statement - 2 : $$0 < f\left( x \right) \le {1 \over {2\sqrt 2 }},$$ for all $$x \in R$$

Let $$f:\left( { - 1,1} \right) \to R$$ be a differentiable function with $$f\left( 0 \right) = - 1$$ and $$f'\left( 0 \right) = 1$$. Let $$g\left( x \right) = {\left[ {f\left( {2f\left( x \right) + 2} \right)} \right]^2}$$. Then $$g'\left( 0 \right) = $$

If two tangents drawn from a point $$P$$ to the parabola $${y^2} = 4x$$ are at right angles, then the locus of $$P$$ is

The circle $${x^2} + {y^2} = 4x + 8y + 5$$ intersects the line $$3x - 4y = m$$ at two distinct points if :

The line $$L$$ given by $${x \over 5} + {y \over b} = 1$$ passes through the point $$\left( {13,32} \right)$$. The line K is parrallel to $$L$$ and has the equation $${x \over c} + {y \over 3} = 1.$$ Then the distance between $$L$$ and $$K$$ is :

A person is to count 4500 currency notes. Let $${a_n}$$ denote the number of notes he counts in the $${n^{th}}$$ minute. If $${a_1}$$ = $${a_2}$$ = ....= $${a_{10}}$$= 150 and $${a_{10}}$$, $${a_{11}}$$,.... are in an AP with common difference - 2, then the time taken by him to count all notes is

There are two urns. Urn A has 3 distinct red balls and urn B has 9 distinct blue balls. From each urn two balls are taken out at random and then transferred to the other. The number of ways in which this can be done is

If $$\alpha $$ and $$\beta $$ are the roots of the equation $${x^2} - x + 1 = 0,$$ then $${\alpha ^{2009}} + {\beta ^{2009}} = $$

Let $$\cos \left( {\alpha + \beta } \right) = {4 \over 5}$$ and $$\sin \,\,\,\left( {\alpha - \beta } \right) = {5 \over {13}},$$ where $$0 \le \alpha ,\,\beta \le {\pi \over 4}.$$
Then $$tan\,2\alpha $$ =

A line $$AB$$ in three-dimensional space makes angles $${45^ \circ }$$ and $${120^ \circ }$$ with the positive $$x$$-axis and the positive $$y$$-axis respectively. If $$AB$$ makes an acute angle $$\theta $$ with the positive $$z$$-axis, then $$\theta $$ equals :

If the vectors $$\overrightarrow a = \widehat i - \widehat j + 2\widehat k,\,\,\,\,\,\overrightarrow b = 2\widehat i + 4\widehat j + \widehat k\,\,\,$$ and $$\,\overrightarrow c = \lambda \widehat i + \widehat j + \mu \widehat k$$ are mutually orthogonal, then $$\,\left( {\lambda ,\mu } \right)$$ is equal to :

Consider the following relations

$R=\{(x, y) \mid x, y$ are real numbers and $x=w y$ for some rational number $w\}$;

$S=\left\{\left(\frac{m}{n}, \frac{p}{q}\right) \mid m, n, p\right.$ and $q$ are integers such that $n, q \neq 0$ and $q m=p m\}$. Then

The combination of gates shown below yields

If a source of power $$4kW$$ produces $${10^{20}}$$ photons/second, the radiation belongs to a part of the spectrum called

A nucleus of mass $$M+$$$$\Delta m$$ is at rest and decays into two daughter nuclei of equal mass $${M \over 2}$$ each. Speed of light is $$c.$$

The speed of daughter nuclei is

A nucleus of mass $$M+$$$$\Delta m$$ is at rest and decays into two daughter nuclei of equal mass $${M \over 2}$$ each. Speed of light is $$c.$$

The binding energy per nucleon for the parent nucleus is $${E_1}$$ and that for the daughter nuclei is $${E_2}.$$ Then

Statement - $$1$$ : When ultraviolet light is incident on a photocell, its stopping potential is $${V_0}$$ and the maximum kinetic energy of the photoelectrons is $${K_{\max }}$$. When the ultraviolet light is replaced by $$X$$-rays, both $${V_0}$$ and $${K_{\max }}$$ increase.

Statement - $$2$$ : Photoelectrons are emitted with speeds ranging from zero to a maximum value because of the range of frequencies present in the incident light.

In the circuit shown below, the key $$K$$ is closed at $$t=0.$$ The current through the battery is

A rectangular loop has a sliding connector $$PQ$$ of length $$l$$ and resistance $$R$$ $$\Omega $$ and it is moving with a speed $$v$$ as shown. The set-up is placed in a uniform magnetic field going into the plane of the paper. The three currents $${I_1},{I_2}$$ and $$I$$ are

An initially parallel cylindrical beam travels in a medium of refractive index $$\mu \left( I \right) = {\mu _0} + {\mu _2}\,I,$$ where $${\mu _0}$$ and $${\mu _2}$$ are positive constants and $$I$$ is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius.

The speed of light in the medium is

An initially parallel cylindrical beam travels in a medium of refractive index $$\mu \left( I \right) = {\mu _0} + {\mu _2}\,I,$$ where $${\mu _0}$$ and $${\mu _2}$$ are positive constants and $$I$$ is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius.

The initial shape of the wavefront of the beam is

An initially parallel cylindrical beam travels in a medium of refractive index $$\mu \left( I \right) = {\mu _0} + {\mu _2}\,I,$$ where $${\mu _0}$$ and $${\mu _2}$$ are positive constants and $$I$$ is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius.

As the beam enters the medium, it will

A point $$P$$ moves in counter-clockwise direction on a circular path as shown in the figure. The movement of $$P$$ is such that it sweeps out a length $$s = {t^3} + 5,$$ where $$s$$ is in metres and $$t$$ is in seconds. The radius of the path is $$20$$ $$m.$$ The acceleration of $$'P'$$ when $$t=2$$ $$s$$ is nearly.

A small particle of mass $$m$$ is projected at an angle $$\theta $$ with the $$x$$-axis with an initial velocity $${v_0}$$ in the $$x$$-$$y$$ plane as shown in the figure. At a time $$t < {{{v_0}\sin \theta } \over g},$$ the angular momentum of the particle is ................,



where $$\widehat i,\widehat j$$ and $$\widehat k$$ are unit vectors along $$x,y$$ and $$z$$-axis respectively.

The figure shows the position$$-$$time $$(x-t)$$ graph of one-dimensional motion of body of mass $$0.4$$ $$kg.$$ The magnitude of each impulse is

Two long parallel wires are at a distance $$2d$$ apart. They carry steady equal currents flowing out of the plane of the paper as shown. The variation of the magnetic field $$B$$ along the line $$XX'$$ is given by

In a series $$LCR$$ circuit $$R = 200\Omega $$ and the voltage and the frequency of the main supply is $$220V$$ and $$50$$ $$Hz$$ respectively. On taking out the capacitance from the circuit the current lags behind the voltage by $${30^ \circ }.$$ On taking out the inductor from the circuit the current leads the voltage by $${30^ \circ }.$$ The power dissipated in the $$LCR$$ circuit is

Two conductors have the same resistance at $${0^ \circ }C$$ but their temperature coefficients of resistance are $${\alpha _1}$$ and $${\alpha _2}.$$ The respective temperature coefficients of their series and parallel combinations are nearly

Let $$C$$ be the capacitance of a capacitor discharging through a resistor $$R.$$ Suppose $${t_1}$$ is the time taken for the energy stored in the capacitor to reduce to half its initial value and $${t_2}$$ is the time taken for the charge to reduce to one-fourth its initial value. Then the ratio $${t_1}/{t_2}$$ will be

A thin semi-circular ring of radius $$r$$ has a positive charges $$q$$ distributed uniformly over it. The net field $$\overrightarrow E $$ at the center $$O$$ is

Let there be a spherically symmetric charge distribution with charge density varying as $$\rho \left( r \right) = {\rho _0}\left( {{5 \over 4} - {r \over R}} \right)$$ upto $$r=R,$$ and $$\rho \left( r \right) = 0$$ for $$r>R,$$ where $$r$$ is the distance from the erigin. The electric field at a distance $$r\left( {r < R} \right)$$ from the origin is given by

The equation of a wave on a string of linear mass density $$0.04\,\,kg\,{m^{ - 1}}$$ is given by $$$y = 0.02\left( m \right)\,\sin \left[ {2\pi \left( {{t \over {0.04\left( s \right)}} - {x \over {0.50\left( m \right)}}} \right)} \right].$$$

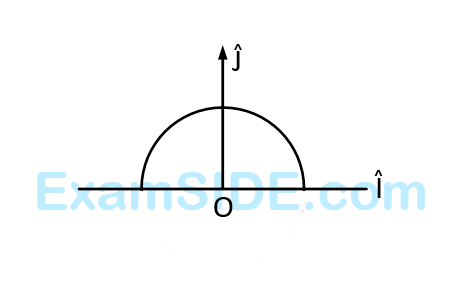
The tension in the string is

A ball is made of a material of density $$\rho $$ where $${\rho _{oil}}\, < \rho < {\rho _{water}}$$ with $${\rho _{oil}}$$ and $${\rho _{water}}$$ representing the densities of oil and water, respectively. The oil and water are immiscible. If the above ball is in equilibrium in a mixture of this oil and water, which of the following pictures represents its equilibrium position?

Two fixed frictionless inclined planes making an angle $${30^ \circ }$$ and $${60^ \circ }$$ with the vertical are shown in the figure. Two blocks $$A$$ and $$B$$ are placed on the two planes. What is the relative vertical acceleration of $$A$$ with respect to $$B$$ ?

Two identical charged spheres are suspended by strings of equal lengths. The strings make an angle of $${30^ \circ }$$ with each other. When suspended in a liquid of density $$0.8g$$ $$c{m^{ - 3}},$$ the angle remains the same. If density of the material of the sphere is $$1.6$$ $$g$$ $$c{m^{ - 3}},$$ the dielectric constant of the liquid is

Statement - 1 : Two particles moving in the same direction do not lose all their energy in a completely inelastic collision.

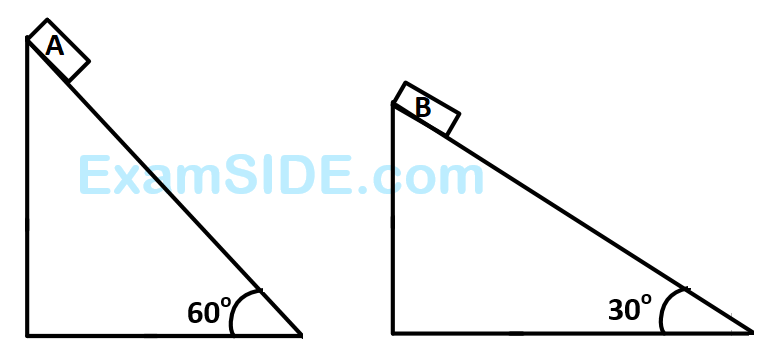
Statement - 2 : Principle of conservation of momentum holds true for all kinds of collisions.

The potential energy function for the force between two atoms in a diatomic molecule is approximately given by $$U\left( x \right) = {a \over {{x^{12}}}} - {b \over {{x^6}}},$$ where $$a$$ and $$b$$ are constants and $$x$$ is the distance between the atoms. If the dissociation energy of the molecule is $$D = \left[ {U\left( {x = \infty } \right) - {U_{at\,\,equilibrium}}} \right],\,\,D$$ is

For a particle in uniform circular motion the acceleration $$\overrightarrow a $$ at a point P(R, θ) on the circle of radius R is (here θ is measured from the x–axis)

A particle is moving with velocity $$\overrightarrow v = k\left( {y\widehat i + x\widehat j} \right)$$, where K is a constant. The general equation for its path is

The respective number of significant figures for the numbers 23.023, 0.0003 and 2.1 $$ \times $$ 10^–3 are