AIEEE 2004
Paper was held on
Sat, Apr 24, 2004 9:30 AM
Chemistry
1
An ideal gas expands in volume from 1$$\times$$10-3 m3 to 1 $$\times$$ 10-2 m3 at 300 K against a constant pressure of 1$$\times$$105 Nm-2. The work done is :
2
The enthalpies of combustion of carbon and carbon monoxide are -393.5 and -283 kJ mol-1
respectively. The enthalpy of formation of carbon monoxide per mole is :
3
The conjugate base of H2PO4- is :
4
What is the equilibrium expression for the reaction
P4 (s) + 5O2 $$\leftrightharpoons$$ P4O10 (s)?
P4 (s) + 5O2 $$\leftrightharpoons$$ P4O10 (s)?
5
For the reaction, CO(g) + Cl2(g) $$\leftrightharpoons$$ COCl2(g) the $${{{K_p}} \over {{K_c}}}$$ is equal to :
6
The equilibrium constant for the reaction N2(g) + O2(g) $$\leftrightharpoons$$ 2NO(g) at temperature T is
4 $$\times$$ 10-4. The value of Kc for the reaction NO(g) $$\leftrightharpoons$$ $$1 \over 2$$N2 (g) + $$1 \over 2$$O2 (g) at the same temperature is :
7
The molar solubility (in ol L-1) of a sparingly soluble salt MX4 is "s". The corresponding solubility product is Ksp. 's' is given in term of Ksp by the relation :
8
Which one of the following has the minimum boiling point?
9
Consider the acidity of the carboxylic acids:
(a) PhCOOH
(b) o – NO2C6H4COOH
(c) p – NO2C6H4COOH
(d) m – NO2C6H4COOH
Which of the following order is correct?
(a) PhCOOH
(b) o – NO2C6H4COOH
(c) p – NO2C6H4COOH
(d) m – NO2C6H4COOH
Which of the following order is correct?
10
Which of the following will have meso-isomer also?
11
Which one the following does not have sp2 hybridized carbon?
12
Which of the following compound is not chiral?
13
Among the properties (a) reducing (b) oxidising (c) complexing, the set of properties shown by CN– ion
towards metal species is :
14
The compound formed on heating chlorobenzene with chloral in the presence concentrated
sulphuric acid is
15
On mixing ethyl acetate with aqueous sodium chloride, the composition of the resultant
solution is
16
Which of the following undergoes reaction with 50% sodium hydroxide solution to give the
corresponding alcohol and acid?
17
Acetyl bromide reacts with excess of CH3MgI followed by treatment with a saturated solution
of NH4Cl given
18
Which one of the following reduced with zinc and hydrochloric acid to give the corresponding
hydrocarbon?
19
Which base is present in RNA but not in DNA?
20
Insulin production and its action in human body are responsible for the level of diabetes. This
compound belongs to which of the following categories?
21
The compound formed in the positive test for nitrogen with the Lassaigne solution of an
organic compound is
22
The correct order of magnetic moments (spin only values in B.M.) among is :
(Atomic numbers: Mn = 25; Fe = 26, Co =27)
(Atomic numbers: Mn = 25; Fe = 26, Co =27)
23
Which of the following is the strongest base ?
24
Amongst the following compounds, the optically active alkane having lowest molecular mass is
25
Rate of the reaction
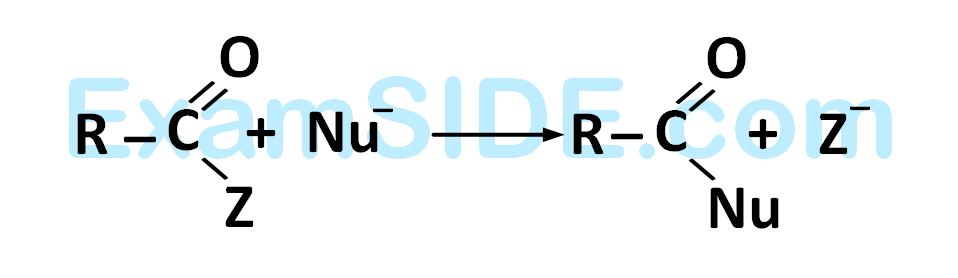
is fastest when $$Z$$ is
is fastest when $$Z$$ is
26
The $$IUPAC$$ name of the compound is
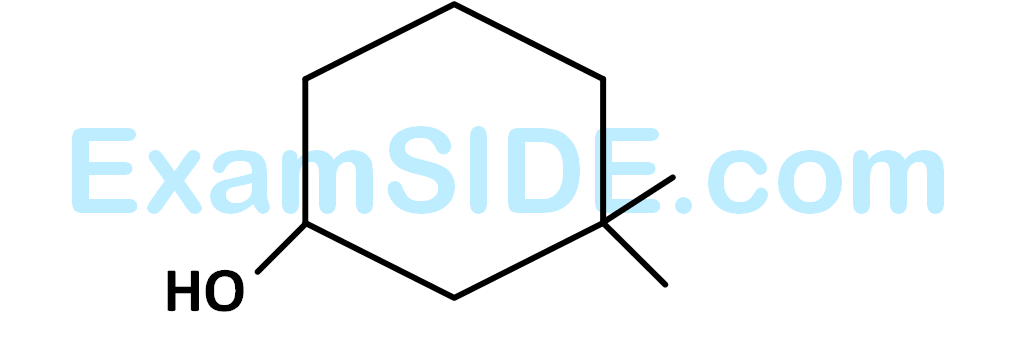

27
Among the following compounds which can be dehydrated very easily is
28
Of the following outer electronic configurations of atoms, the highest oxidation state is achieved by which one of them?
29
The rate equation for the reaction 2A + B $$\to$$ C is found to be: rate k[A][B]. The correct
statement in relation to this reaction is that the
30
Identify the correct statements regarding enzymes
31
Which of the following liquid pairs shows a positive deviation from Raoult’s law?
32
Which one of the following statements is false?
33
Which one of the following aqueous solutions will exhibit highest boiling point?
34
For which of the following parameters the structural isomers C2H5OH and CH3OCH3 would
be expected to have the same values? (Assume ideal behaviour)
35
In a hydrogen – oxygen fuel cell, combustion of hydrogen occurs to :
36
Consider the following Eo values
$$E_{F{e^{3 + }}/F{e^{2 + }}}^o$$ = 0.77 V;
$$E_{S{n^{2 + }}/S{n}}^o$$ = -0.14 V
Under standard conditions the potential for the reaction
Sn(s) + 2Fe3+(aq) $$\to$$ 2Fe2+(aq) + Sn2+(aq) is :
$$E_{F{e^{3 + }}/F{e^{2 + }}}^o$$ = 0.77 V;
$$E_{S{n^{2 + }}/S{n}}^o$$ = -0.14 V
Under standard conditions the potential for the reaction
Sn(s) + 2Fe3+(aq) $$\to$$ 2Fe2+(aq) + Sn2+(aq) is :
37
The standard e.m.f of a cell, involving one electron change is found to be 0.591 V at 25oC.
The equilibrium constant of the reaction is (F = 96,500 C mol-1: R = 8.314 JK-1 mol-1)
38
The limiting molar conductivities Λ° for NaCl, KBr and KCl are 126, 152 and 150 S cm2 mol-1 respectively. The Λ° for NaBr is
39
In a cell that utilises the reaction Zn(s) + 2H+
(aq) $$\to$$ Zn2+(aq) + H2(g) addition of H2SO4 to cathode compartment, will
40
The $$E_{{M^{3 + }}/{M^{2 + }}}^o$$ values for Cr, Mn, Fe and Co are – 0.41, +1.57, + 0.77 and +1.97 V
respectively. For which one of these metals the change in oxidation state form +2 to +3 is
easiest?
41
In a first order reaction, the concentration of the reactant decreases from 0.8 M to 0.4 M in 15
minutes. The time taken for the concentration to change from 0.1 M to 0.025 M is
42
Consider the following nuclear reactions
$${}_{92}^{238}M \to {}_Y^XN + 2{}_2^4He$$
$${}_Y^XN \to {}_B^AL + 2{\beta ^ + }$$
The number of neutrons in the element L is
$${}_{92}^{238}M \to {}_Y^XN + 2{}_2^4He$$
$${}_Y^XN \to {}_B^AL + 2{\beta ^ + }$$
The number of neutrons in the element L is
43
The half – life of a radioisotope is four hours. If the initial mass of the isotope was 200 g, the
mass remaining after 24 hours undecayed is
44
Beryllium and aluminium exhibit many properties which are similar. But the two elements
differ in :
45
Which one the following statement regarding helium is incorrect?
46
Excess of KI reacts with CuSO4 solution and then Na2S2O3 solution is added to it. Which of the statements is incorrect for this reaction?
47
Cerium (Z = 58) is an important member of the lanthanoids. Which of the following
statements about cerium is incorrect?
48
Which one of the following complexes in an outer orbital complex?
49
Which one the following has largest number of isomers? (R = alkyl group, en = ethylenediamine)
50
Coordination compound have great importance in biological systems. In this context which of
the following statements is incorrect?
51
The coordination number of central metal atom in a complex is determined by :
52
6.02 $$\times$$ 1020 molecules of urea are present in 100 ml of its solution. The concentration of urea solution is
(Avogadro constant, NA = 6.02 $$\times$$ 1023 mol-1)
(Avogadro constant, NA = 6.02 $$\times$$ 1023 mol-1)
53
To neutralise completely 20 mL of 0.1 M aqueous solution of phosphorous acid (H3PO3), the volume of 0.1 M aqueous KOH solution required is
54
The ammonia evolved from the treatment of 0.30 g of an organic compound for the estimation of nitrogen was passed in 100 mL of 0.1 M sulphuric acid. The excess of acid required 20 mL of 0.5 M sodium hydroxide solution for complete neutralization. The organic compound is
55
Which of the following sets of quantum numbers is correct for an electron in 4f orbital?
56
Consider the ground state of Cr atom (Z = 24). The number of electrons with the azimuthal quantum numbers, l = 1 and 2 are respectively
57
The wavelength of the radiation emitted when in a hydrogen atom electron falls from infinity to stationary state 1, would be (Rydberg constant = 1.097 $$\times$$ 107 m-1)
58
Which one of the following sets of ions represents the collection of isoelectronic species? (Atomic nos. : F = 9, Cl = 17, Na = 11, Mg = 12, Al = 13, K = 19, Ca = 20, Sc = 21)
59
Which one of the following ions has the highest value of ionic radius?
60
Among Al2O3, SiO2, P2O3 and SO2 the correct order of acid strength is
61
The formation of the oxide ion O2-(g) requires first an exothermic and then an endothermic
step as shown below
O(g) + e- = $$O_{(g)}^{-}$$ $$\Delta $$Ho = -142 kJmol-1
$$O_{(g)}^{-}$$ + e- = $$O_{(g)}^{2-}$$ $$\Delta $$Ho = 844 kJmol-1
This because
O(g) + e- = $$O_{(g)}^{-}$$ $$\Delta $$Ho = -142 kJmol-1
$$O_{(g)}^{-}$$ + e- = $$O_{(g)}^{2-}$$ $$\Delta $$Ho = 844 kJmol-1
This because
62
The correct order of bond angles (smallest first) in H2S, NH3, BF3 and SiH4 is
63
The bond order in NO is 2.5 while that in NO+ is 3. Which of the following statements is true for these two species?
64
The states of hybridization of boron and oxygen atoms in boric acid (H3BO3) are respectively
65
Which one of the following has the regular tetrahedral structure?
(Atomic nos : B = 5, S = 16, Ni = 28, Xe = 54)
(Atomic nos : B = 5, S = 16, Ni = 28, Xe = 54)
66
The maximum number of 90° angles between bond pair of electrons is observed in
Mathematics
1
The domain of the function
$$f\left( x \right) = {{{{\sin }^{ - 1}}\left( {x - 3} \right)} \over {\sqrt {9 - {x^2}} }}$$
$$f\left( x \right) = {{{{\sin }^{ - 1}}\left( {x - 3} \right)} \over {\sqrt {9 - {x^2}} }}$$
2
The range of the function f(x) = $${}^{7 - x}{P_{x - 3}}$$ is
3
If $$f:R \to S$$, defined by
$$f\left( x \right) = \sin x - \sqrt 3 \cos x + 1$$,
is onto, then the interval of $$S$$ is
$$f\left( x \right) = \sin x - \sqrt 3 \cos x + 1$$,
is onto, then the interval of $$S$$ is
4
The graph of the function y = f(x) is symmetrical about the line x = 2, then
5
Let $$f(x) = {{1 - \tan x} \over {4x - \pi }}$$, $$x \ne {\pi \over 4}$$, $$x \in \left[ {0,{\pi \over 2}} \right]$$.
If $$f(x)$$ is continuous in $$\left[ {0,{\pi \over 2}} \right]$$, then $$f\left( {{\pi \over 4}} \right)$$ is
If $$f(x)$$ is continuous in $$\left[ {0,{\pi \over 2}} \right]$$, then $$f\left( {{\pi \over 4}} \right)$$ is
6
If $$\mathop {\lim }\limits_{x \to \infty } {\left( {1 + {a \over x} + {b \over {{x^2}}}} \right)^{2x}} = {e^2}$$, then the value of $$a$$ and $$b$$, are
7
Consider the following statements:
(a) Mode can be computed from histogram
(b) Median is not independent of change of scale
(c) Variance is independent of change of origin and scale.
Which of these is/are correct?
(a) Mode can be computed from histogram
(b) Median is not independent of change of scale
(c) Variance is independent of change of origin and scale.
Which of these is/are correct?
8
In a series of 2n observations, half of them equal $$a$$ and remaining half equal $$–a$$. If the
standard deviation of the observations is 2, then $$|a|$$ equals
9
Let $$\alpha ,\,\beta $$ be such that $$\pi < \alpha - \beta < 3\pi $$.
If $$sin{\mkern 1mu} \alpha + \sin \beta = - {{21} \over {65}}$$ and $$\cos \alpha + \cos \beta = - {{27} \over {65}}$$ then the value of $$\cos {{\alpha - \beta } \over 2}$$ :
If $$sin{\mkern 1mu} \alpha + \sin \beta = - {{21} \over {65}}$$ and $$\cos \alpha + \cos \beta = - {{27} \over {65}}$$ then the value of $$\cos {{\alpha - \beta } \over 2}$$ :
10
The value of $$\int\limits_{ - 2}^3 {\left| {1 - {x^2}} \right|dx} $$ is
11
If $$x = {e^{y + {e^y} + {e^{y + .....\infty }}}}$$ , $$x > 0,$$ then $${{{dy} \over {dx}}}$$ is
12
A point on the parabola $${y^2} = 18x$$ at which the ordinate increases at twice the rate of the abscissa is
13
Let $$A = \left( {\matrix{
0 & 0 & { - 1} \cr
0 & { - 1} & 0 \cr
{ - 1} & 0 & 0 \cr
} } \right)$$. The only correct
statement about the matrix $$A$$ is
14
Let $$A = \left( {\matrix{
1 & { - 1} & 1 \cr
2 & 1 & { - 3} \cr
1 & 1 & 1 \cr
} } \right).$$ and $$10$$ $$B = \left( {\matrix{
4 & 2 & 2 \cr
{ - 5} & 0 & \alpha \cr
1 & { - 2} & 3 \cr
} } \right)$$. if $$B$$ is
the inverse of matrix $$A$$, then $$\alpha $$ is
15
If $${a_1},{a_2},{a_3},.........,{a_n},......$$ are in G.P., then the value of the determinant
$$\left| {\matrix{ {\log {a_n}} & {\log {a_{n + 1}}} & {\log {a_{n + 2}}} \cr {\log {a_{n + 3}}} & {\log {a_{n + 4}}} & {\log {a_{n + 5}}} \cr {\log {a_{n + 6}}} & {\log {a_{n + 7}}} & {\log {a_{n + 8}}} \cr } } \right|,$$ is
16
If $$\int {{{\sin x} \over {\sin \left( {x - \alpha } \right)}}dx = Ax + B\log \sin \left( {x - \alpha } \right), + C,} $$ then value of
$$(A, B)$$ is
$$(A, B)$$ is
17
$$\int {{{dx} \over {\cos x - \sin x}}} $$ is equal to
18
The eccentricity of an ellipse, with its centre at the origin, is $${1 \over 2}$$. If one of the directrices is $$x=4$$, then the equation of the ellipse is :
19
The value of $$I = \int\limits_0^{\pi /2} {{{{{\left( {\sin x + \cos x} \right)}^2}} \over {\sqrt {1 + \sin 2x} }}dx} $$ is
20
If $$\int\limits_0^\pi {xf\left( {\sin x} \right)dx = A\int\limits_0^{\pi /2} {f\left( {\sin x} \right)dx,} } $$ then $$A$$ is
21
If $$f\left( x \right) = {{{e^x}} \over {1 + {e^x}}},{I_1} = \int\limits_{f\left( { - a} \right)}^{f\left( a \right)} {xg\left\{ {x\left( {1 - x} \right)} \right\}dx} $$
and $${I_2} = \int\limits_{f\left( { - a} \right)}^{f\left( a \right)} {g\left\{ {x\left( {1 - x} \right)} \right\}dx} ,$$ then the value of $${{{I_2}} \over {{I_1}}}$$ is
and $${I_2} = \int\limits_{f\left( { - a} \right)}^{f\left( a \right)} {g\left\{ {x\left( {1 - x} \right)} \right\}dx} ,$$ then the value of $${{{I_2}} \over {{I_1}}}$$ is
22
The area of the region bounded by the curves
$$y = \left| {x - 2} \right|,x = 1,x = 3$$ and the $$x$$-axis is :
$$y = \left| {x - 2} \right|,x = 1,x = 3$$ and the $$x$$-axis is :
23
Solution of the differential equation $$ydx + \left( {x + {x^2}y} \right)dy = 0$$ is
24
The probability that $$A$$ speaks truth is $${4 \over 5},$$ while the probability for $$B$$ is $${3 \over 4}.$$ The probability that they contradict each other when asked to speak on a fact is :
25
A particle acted on by constant forces $$4\widehat i + \widehat j - 3\widehat k$$ and $$3\widehat i + \widehat j - \widehat k$$ is displaced from the point $$\widehat i + 2\widehat j + 3\widehat k$$ to the point $$\,5\widehat i + 4\widehat j + \widehat k.$$ The total work done by the forces is :
26
Let $$\overrightarrow u ,\overrightarrow v ,\overrightarrow w $$ be such that $$\left| {\overrightarrow u } \right| = 1,\,\,\,\left| {\overrightarrow v } \right|2,\,\,\,\left| {\overrightarrow w } \right|3.$$ If the projection $${\overrightarrow v }$$ along $${\overrightarrow u }$$ is equal to that of $${\overrightarrow w }$$ along $${\overrightarrow u }$$ and $${\overrightarrow v },$$ $${\overrightarrow w }$$ are perpendicular to each other then $$\left| {\overrightarrow u - \overrightarrow v + \overrightarrow w } \right|$$ equals :
27
Let $$\overrightarrow a ,\overrightarrow b $$ and $$\overrightarrow c $$ be three non-zero vectors such that no two of these are collinear. If the vector $$\overrightarrow a + 2\overrightarrow b $$ is collinear with $$\overrightarrow c $$ and $$\overrightarrow b + 3\overrightarrow c $$ is collinear with $$\overrightarrow a $$ ($$\lambda $$ being some non-zero scalar) then $$\overrightarrow a + 2\overrightarrow b + 6\overrightarrow c $$ equals to :
28
Let $${{T_r}}$$ be the rth term of an A.P. whose first term is a and common difference is d. If for some positive integers m, n, $$m \ne n,\,\,{T_m} = {1 \over n}\,\,and\,{T_n} = {1 \over m},\,$$ then a - d equals
29
If $$u = \sqrt {{a^2}{{\cos }^2}\theta + {b^2}{{\sin }^2}\theta } + \sqrt {{a^2}{{\sin }^2}\theta + {b^2}{{\cos }^2}\theta } $$
then the difference between the maximum and minimum values of $${u^2}$$ is given by :
then the difference between the maximum and minimum values of $${u^2}$$ is given by :
30
A line makes the same angle $$\theta $$, with each of the $$x$$ and $$z$$ axis.
If the angle $$\beta \,$$, which it makes with y-axis, is such that $$\,{\sin ^2}\beta = 3{\sin ^2}\theta ,$$ then $${\cos ^2}\theta $$ equals :
If the angle $$\beta \,$$, which it makes with y-axis, is such that $$\,{\sin ^2}\beta = 3{\sin ^2}\theta ,$$ then $${\cos ^2}\theta $$ equals :
31
Let z and w be complex numbers such that $$\overline z + i\overline w = 0$$ and arg zw = $$\pi $$. Then arg z equals :
32
If $$z = x - iy$$ and $${z^{{1 \over 3}}} = p + iq$$, then
$${{\left( {{x \over p} + {y \over q}} \right)} \over {\left( {{p^2} + {q^2}} \right)}}$$ is equal to :
$${{\left( {{x \over p} + {y \over q}} \right)} \over {\left( {{p^2} + {q^2}} \right)}}$$ is equal to :
33
If $$\,\left| {{z^2} - 1} \right| = {\left| z \right|^2} + 1$$, then z lies on :
34
Let two numbers have arithmetic mean 9 and geometric mean 4. Then these numbers are the roots of the quadratic equation
35
If $$\left( {1 - p} \right)$$ is a root of quadratic equation $${x^2} + px + \left( {1 - p} \right) = 0$$ then its root are
36
If one root of the equation $${x^2} + px + 12 = 0$$ is 4, while the equation $${x^2} + px + q = 0$$ has equal roots,
then the value of $$'q'$$ is
then the value of $$'q'$$ is
37
How many ways are there to arrange the letters in the word GARDEN with vowels in alphabetical order
38
The number of ways of distributing 8 identical balls in 3 distinct boxes so that none of the boxes is empty is
39
The coefficient of the middle term in the binomial expansion in powers of $$x$$ of $${\left( {1 + \alpha x} \right)^4}$$ and $${\left( {1 - \alpha x} \right)^6}$$ is the same if $$\alpha $$ equals
40
The coefficient of $${x^n}$$ in expansion of $$\left( {1 + x} \right){\left( {1 - x} \right)^n}$$ is
41
The equation of the straight line passing through the point $$(4, 3)$$ and making intercepts on the co-ordinate axes whose sum is $$-1$$ is :
42
Let $$A\left( {2, - 3} \right)$$ and $$B\left( {-2, 1} \right)$$ be vertices of a triangle $$ABC$$. If the centroid of this triangle moves on the line $$2x + 3y = 1$$, then the locus of the vertex $$C$$ is the line :
43
If the lines 2x + 3y + 1 + 0 and 3x - y - 4 = 0 lie along diameter of a circle of circumference $$10\,\pi $$, then the equation of the circle is :
44
If a circle passes through the point (a, b) and cuts the circle $${x^2}\, + \,{y^2} = 4$$ orthogonally, then the locus of its centre is :
45
Intercept on the line y = x by the circle $${x^2}\, + \,{y^2} - 2x = 0$$ is AB. Equation of the circle on AB as a diameter is :
46
If $$a \ne 0$$ and the line $$2bx+3cy+4d=0$$ passes through the points of intersection of the parabolas $${y^2} = 4ax$$ and $${x^2} = 4ay$$, then :
47
Let $$\overrightarrow a ,\overrightarrow b $$ and $$\overrightarrow c $$ be non-zero vectors such that $$\left( {\overrightarrow a \times \overrightarrow b } \right) \times \overrightarrow c = {1 \over 3}\left| {\overrightarrow b } \right|\left| {\overrightarrow c } \right|\overrightarrow a \,\,.$$ If $$\theta $$ is the acute angle between the vectors $${\overrightarrow b }$$ and $${\overrightarrow c },$$ then $$sin\theta $$ equals :
48
A line with direction cosines proportional to $$2,1,2$$ meets each of the lines $$x=y+a=z$$ and $$x+a=2y=2z$$ . The co-ordinates of each of the points of intersection are given by :
49
If the straight lines
$$x=1+s,y=-3$$$$ - \lambda s,$$ $$z = 1 + \lambda s$$ and $$x = {t \over 2},y = 1 + t,z = 2 - t,$$ with parameters $$s$$ and $$t$$ respectively, are co-planar, then $$\lambda $$ equals :
$$x=1+s,y=-3$$$$ - \lambda s,$$ $$z = 1 + \lambda s$$ and $$x = {t \over 2},y = 1 + t,z = 2 - t,$$ with parameters $$s$$ and $$t$$ respectively, are co-planar, then $$\lambda $$ equals :
50
Let $R=\{(1,3),(4,2),(2,4),(2,3),(3,1)\}$ be a relation on the set $A=\{1,2,3,4\}$. The relation $R$ is :
Physics
1
An electromagnetic wave of frequency $$v=3.0$$ $$MHz$$ passes from vacuum into a dielectric medium with permittivity $$ \in = 4.0.$$ Then
2
The maximum number of possible interference maxima for slit-separation equal to twice the wavelength in Young's double-slit experiment, is :
3
The work function of a substance is $$4.0$$ $$eV.$$ The longest wavelength of light that can cause photo-electron emission from this substance is approximately.
4
A radiation of energy $$E$$ falls normally on a perfectly reflecting surface. The momentum transferred to the surface is
5
According to Einstein's photoelectric equation, the plot of the kinetic energy of the emitted photo electrons from a metal $$Vs$$ the frequency, of the incident radiation gives as straight the whose slope
6
The binding energy per nucleon of deuteron $$\left( {{}_1^2\,H} \right)$$ and helium nucleus $$\left( {{}_2^4\,He} \right)$$ is $$1.1$$ $$MeV$$ and $$7$$ $$MeV$$ respectively. If two deuteron nuclei react to form a single helium nucleus, then the energy released is
7
An $$\alpha $$-particle of energy $$5$$ $$MeV$$ is scattered through $${180^ \circ }$$ by a fixed uranium nucleus. The distance of closest approach is of the order of
8
A piece of copper and another of germanium are cooled from room temperature to $$77K,$$ the resistance of
9
The manifestation of band structure in solids is due to
10
The angle of incidence at which reflected light is totally polarized for reflection from air to glass (refractive index $$n$$) is :
11
When $$p$$-$$n$$ junction diode is forward biased then
12
A current $$i$$ ampere flows along an infinitely long straight thin walled tube, then the magnetic induction at any point inside the tube is
13
Four charges equal to -$$Q$$ are placed at the four corners of a square and a charge $$q$$ is at its center. If the system is in equilibrium the value of $$q$$ is
14
A charged oil drop is suspended in a uniform field of $$3 \times {10^4}$$ $$v/m$$ so that it neither falls nor rises. The charge on the drop will be (Take the mass of the charge $$ = 9.9 \times {10^{ - 15}}\,\,kg$$ and $$g = 10\,m/{s^2}$$)
15
An electric current is passed through a circuit containing two wires of the same material, connected in parallel. If the lengths and radii are in the ratio of $${4 \over 3}$$ and $${2 \over 3}$$, then the ratio of the current passing through the wires will be
16
The resistance of the series combination of two resistances is $$S.$$ When they are jointed in parallel the total resistance is $$P.$$ If $$S = nP$$ then the Minimum possible value of $$n$$ is
17
The total current supplied to the circuit by the battery is
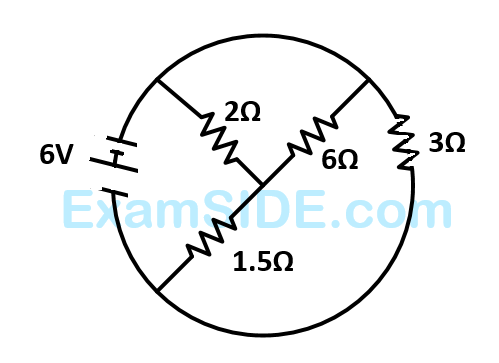

18
Thermistors are usually made of
19
Time taken by a $$836$$ $$W$$ heater to heat one litre of water from $$10{}^ \circ C$$ to $$40{}^ \circ C$$ is
20
In a meter bridge experiment null point is obtained at $$20$$ $$cm$$, from one end of the wire when resistance $$X$$ is balanced against another resistance $$Y.$$ If $$X < Y$$, then where will be the new position of the null point from the same end, if one decides to balance a resistance of $$4$$ $$X$$ against $$Y$$
21
The thermo $$emf$$ of a thermocouple varies with temperature $$\theta $$ of the hot junction as $$E = a\theta + b{\theta ^2}$$ in volts where the ratio $$a/b$$ is $${700^ \circ }C.$$ If the cold junction is kept at $${0^ \circ }C,$$ then the neutral temperature is
22
The electrochemical equivalent of a metal is $${3.35109^{ - 7}}$$ $$kg$$ per Coulomb. The mass of the metal liberated at the cathode when a $$3A$$ current is passed for $$2$$ seconds will be
23
A material $$'B'$$ has twice the specific resistance of $$'A'.$$ A circular wire made of $$'B'$$ has twice the diameter of a wire made of $$'A'$$. Then for the two wires to have the same resistance, the ratio $${l \over B}/{l \over A}$$ of their respective lengths must be
24
The Kirchhoff's first law $$\left( {\sum i = 0} \right)$$ and second law $$\left( {\sum iR = \sum E} \right),$$ where the symbols have their usual meanings, are respectively based on
25
Curie temperature is the temperature above which
26
A long wire carries a steady current. It is bent into a circle of one turn and the magnetic field at the centre of the coil is $$B.$$ It is then bent into a circular loop of $$n$$ turns. The magnetic field at the center of the coil will be
27
The magnetic field due to a current carrying circular loop of radius $$3$$ $$cm$$ at a point on the axis at a distance of $$4$$ $$cm$$ from the centre is $$54\,\mu T.$$ What will be its value at the center of loop?
28
The length of a magnet is large compared to its width and breadth. The time period of its oscillation in a vibration magnetometer is $$2s.$$ The magnet is cut along its length into three equal parts and these parts are then placed on each other with their like poles together. The time period of this combination will be
29
Two long conductors, separated by a distance $$d$$ carry current $${I_1}$$ and $${I_2}$$ in the same direction. They exert a force $$F$$ on each other. Now the current in one of them is increased to two times and its direction is reversed. The distance is also increased to $$3d$$. The new value of the force between them is
30
The materials suitable for making electromagnets should have
31
In an $$LCR$$ series $$a.c.$$ circuit, the voltage across each of the components, $$L,C$$ and $$R$$ is $$50V$$. The voltage across the $$L.C$$ combination will be :
32
Alternating current can not be measured by $$D.C.$$ ammeter because
33
A coil having $$n$$ turns and resistance $$R\Omega $$ is connected with a galvanometer of resistance $$4R\Omega .$$ This combination is moved in time $$t$$ seconds from a magnetic field $${W_1}$$ weber to $${W_2}$$ weber. The induced current in the circuit is
34
In a uniform magnetic field of induction $$B$$ a wire in the form of a semicircle of radius $$r$$ rotates about the diameter of the circle with an angular frequency $$\omega .$$ The axis of rotation is perpendicular to the field. If the total resistance of the circuit is $$R,$$ the mean power generated per period of rotation is
35
In a $$LCR$$ circuit capacitance is changed from $$C$$ to $$2$$ $$C$$. For the resonant frequency to remain unchaged, the inductance should be changed from $$L$$ to
36
A metal conductor of length $$1$$ $$m$$ rotates vertically about one of its ends at angular velocity $$5$$ radians per second. If the horizontal component of earth's magnetic field is $$0.2 \times {10^{ - 4}}T,$$ then the $$e.m.f.$$ developed between the two ends of the conductor is
37
A plano convex lens of refractive index $$1.5$$ and radius of curvature $$30$$ $$cm$$. Is silvered at the curved surface. Now this lens has been used to form the image of an object. At what distance from this lens an object be placed in order to have a real image of size of the object
38
A light ray is incident perpendicularly to one face of a $${90^ \circ }$$ prism and is totally internally reflected at the glass-air interface. If the angle of reflection is $${45^ \circ }$$, we conclude that the refractive index $$n$$


39
Two spherical conductors $$B$$ and $$C$$ having equal radii and carrying equal charges on them repel each other with a force $$F$$ when kept apart at some distance. A third spherical conductor having same radius as that $$B$$ but uncharged is brought in contact with $$B,$$ then brought in correct with $$C$$ and finally removed away from both. The new force of repulsion between $$B$$ and $$C$$ is
40
Spherical balls of radius $$R$$ are falling in a viscous fluid of viscosity $$\eta $$ with a velocity $$v.$$ The retarding viscous force acting on the spherical ball is
41
A particle moves in a straight line with retardation proportional to its displacement. Its loss of kinetic energy for any displacement $$x$$ is proportional to
42
A uniform chain of length $$2$$ $$m$$ is kept on a table such that a length of $$60$$ $$cm$$ hangs freely from the edge of the table. The total mass of the chain is $$4$$ $$kg.$$ What is the work done in pulling the entire chain on the table?
43
A force $$\overrightarrow F = \left( {5\overrightarrow i + 3\overrightarrow j + 2\overrightarrow k } \right)N$$ is applied over a particle which displaces it from its origin to the point $$\overrightarrow r = \left( {2\overrightarrow i - \overrightarrow j } \right)m.$$ The work done on the particle in joules is
44
A body of mass $$' m ',$$ acceleration uniformly from rest to $$'{v_1}'$$ in time $${T}$$. The instantaneous power delivered to the body as a function of time is given by
45
A particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle, the motion of the particles takes place in a plane. It follows that
46
A machine gun fires a bullet of mass $$40$$ $$g$$ with a velocity $$1200m{s^{ - 1}}.$$ The man holding it can exert a maximum force of $$144$$ $$N$$ on the gun. How many bullets can he fire per second at the most?
47
One solid sphere $$A$$ and another hollow sphere $$B$$ are of same mass and same outer radii. Their moment of inertia about their diameters are respectively $${I_A}$$ and $${I_B}$$ such that
48
A solid sphere is rotating in free space. If the radius of the sphere is increased keeping mass same which on of the following will not be affected ?
49
A satellite of mass $$m$$ revolves around the earth of radius $$R$$ at a height $$x$$ from its surface. If $$g$$ is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
50
Suppose the gravitational force varies inversely as the nth power of distance. Then the time period of a planet in circular orbit of radius $$R$$ around the sun will be proportional to
51
If $$g$$ is the acceleration due to gravity on the earth's surface, the gain in the potential energy of an object of mass $$m$$ raised from the surface of the earth to a height equal to the radius $$R$$ of the earth is
52
The time period of an earth satellite in circular orbit is independent of
53
A wire fixed at the upper end stretches by length $$l$$ by applying a force $$F.$$ The work done in stretching is
54
If two soap bubbles of different radii are connected by a tube
55
If the temperature of the sun were to increase from $$T$$ to $$2T$$ and its radius from $$R$$ to $$2R$$, then the ratio of the radiant energy received on earth to what it was previously will be
56
One mole of ideal monatomic gas $$\left( {\gamma = 5/3} \right)$$ is mixed with one mole of diatomic gas $$\left( {\gamma = 7/5} \right)$$. What is $$\gamma $$ for the mixture? $$\gamma $$ Denotes the ratio of specific heat at constant pressure, to that at constant volume
57
Two thermally insulated vessels $$1$$ and $$2$$ are filled with air at temperatures $$\left( {{T_1},{T_2}} \right),$$ volume $$\left( {{V_1},{V_2}} \right)$$ and pressure $$\left( {{P_1},{P_2}} \right)$$ respectively. If the value joining the two vessels is opened, the temperature inside the vessel at equilibrium will be
58
Which of the following statements is correct for any thermodynamic system ?
59
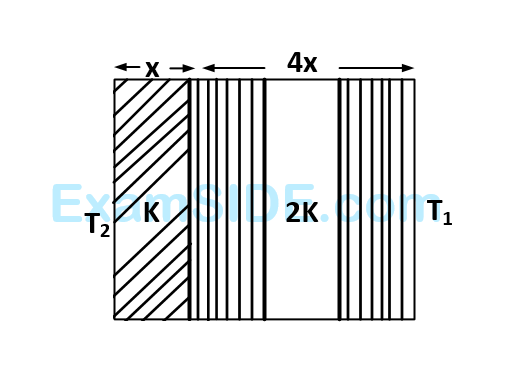
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity $$K$$ and $$2K$$ and thickness $$x$$ and $$4x,$$ respectively, are $${T_2}$$ and $${T_1}\left( {{T_2} > {T_1}} \right).$$ The rate of heat transfer through the slab, in a steady state is $$\left( {{{A\left( {{T_2} - {T_1}} \right)K} \over x}} \right)f,$$ with $$f$$ equal to

60
The bob of a simple pendulum executes simple harmonic motion in water with a period $$t,$$ while the period of oscillation of the bob is $${t_0}$$ in air. Neglecting frictional force of water and given that the density of the bob is $$\left( {4/3} \right) \times 1000\,\,kg/{m^3}.$$ What relationship between $$t$$ and $${t_0}$$ is true
61
The total energy of particle, executing simple harmonic motion is
62
A particle at the end of a spring executes $$S.H.M$$ with a period $${t_1}$$. While the corresponding period for another spring is $${t_2}$$. If the period of oscillation with the two springs in series is $$T$$ then
63
A particle of mass $$m$$ is attached to a spring (of spring constant $$k$$) and has a natural angular frequency $${\omega _0}.$$ An external force $$F(t)$$ proportional to $$\cos \,\omega t\left( {\omega \ne {\omega _0}} \right)$$ is applied to the oscillator. The time displacement of the oscillator will be proportional to
64
The displacement $$y$$ of a particle in a medium can be expressed as, $$y = {10^{ - 6}}\,\sin $$ $$\left( {100t + 20x + {\pi \over 4}} \right)$$ $$m$$ where $$t$$ is in second and $$x$$ in meter. The speed of the wave is
65
A charge particle $$'q'$$ is shot towards another charged particle $$'Q'$$ which is fixed, with a speed $$'v'$$. It approaches $$'Q'$$ upto a closest distance $$r$$ and then returns. If $$q$$ were given a speed of $$'2v'$$ the closest distances of approaches would be
66
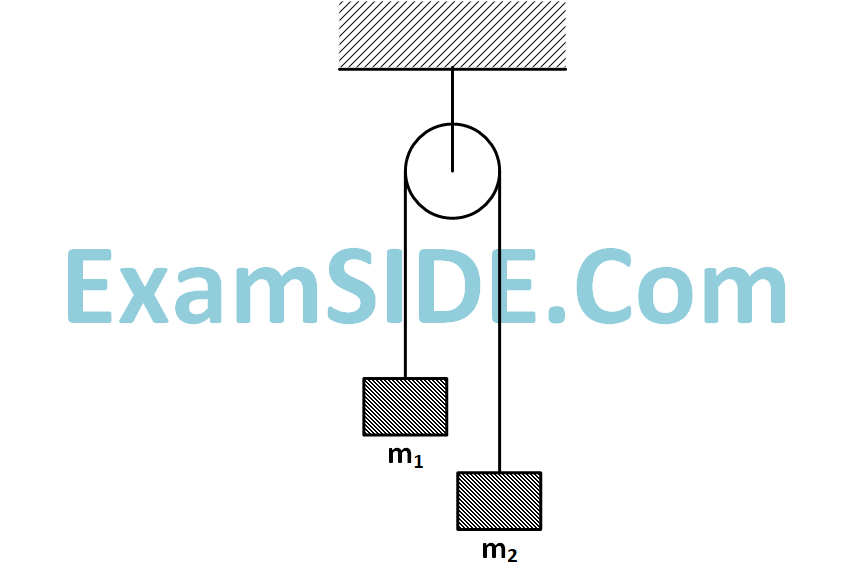
Two masses $${m_1} = 5kg$$ and $${m_2} = 4.8kg$$ tied to a string are hanging over a light frictionless pulley. What is the acceleration of the masses when left free to move? $$\left( {g = 9.8m/{s^2}} \right)$$

67
Which one of the following represents the correct dimensions of the coefficient of viscosity?
68
A ball is released from the top of a tower of height h meters. It takes T seconds to reach the
ground. What is the position of the ball in $${T \over 3}$$ seconds?
69
If $$\overrightarrow A \times \overrightarrow B = \overrightarrow B \times \overrightarrow A $$, then the angle beetween A and B is
70
A projectile can have the same range 'R' for two angles of projection. If T1 and T2 be the time
of flights in the two cases, then the product of the two time of flights is directly proportional to
71
Which of the following statements is FALSE for a particle moving in a circle with a constant
angular speed?
72
An automobile travelling with speed of 60 km/h, can brake to stop within a distance of 20 m.
If the car is going twice as fast, i.e 120 km/h, the stopping distance will be
73
A ball is thrown from a point with a speed ν0 at an angle of projection θ. From the same point
and at the same instant person starts running with a constant speed $${{{v_0}} \over 2}$$ to catch the ball.
Will the person be able to catch the ball? If yes, what should be the angle of projection θ?
74
A block rests on a rough inclined plane `making an angle of $${30^ \circ }$$ with the horizontal. The coefficient of static friction between the block and the plane is $$0.8.$$ If the frictionless force on the block is $$10$$ $$N,$$ the mass of the block (in $$kg$$) is $$\left( {take\,\,\,g\, = \,10\,\,m/{s^2}} \right)$$