JEE Main 2021 (Online) 17th March Morning Shift
Paper was held on
Wed, Mar 17, 2021 3:30 AM
Chemistry
1
The absolute value of the electron gain enthalpy of halogens satisfies :
2
What is the spin-only magnetic moment value (BM) of a divalent metal ion with atomic number 25, in it's aqueous solution?
3
Hoffmann bromomide degradation of benzamide gives product A, which upon heating with CHCl3 and NaOH gives product B.
The structures of A and B are :
The structures of A and B are :
4
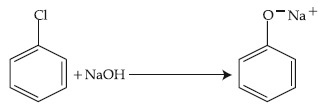
The above reaction requires which of the following reaction conditions?
5
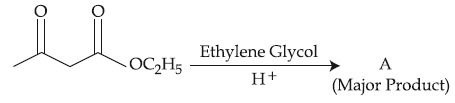
The product ''A'' in the above reaction is :
6
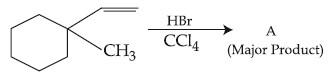
Product ''A'' in the above chemical reaction is :
7
Which of the following compound CANNOT act as a Lewis base?
8
Given below are two statements :
Statement I : Potassium permanganate on heating at 573K forms potassium manganate.
Statement II : Both potassium permanganate and potassium manganate are tetrahedral and paramagnetic in nature.
In the light of the above statements, choose the most appropriate answer from the options given below :
Statement I : Potassium permanganate on heating at 573K forms potassium manganate.
Statement II : Both potassium permanganate and potassium manganate are tetrahedral and paramagnetic in nature.
In the light of the above statements, choose the most appropriate answer from the options given below :
9
Mesityl oxide is a common name of :
10
Which of the following is an aromatic compound?
11
A central atom in a molecule has two lone pairs of electrons and forms three single bonds. The shape of this molecule is :
12
Given below are two statements :
Statement I : Retardation factor (Rf) can be measured in meter/centimeter.
Statement II : Rf value of a compound remains constant in all solvents.
Choose the most appropriate answer from the options given below :
Statement I : Retardation factor (Rf) can be measured in meter/centimeter.
Statement II : Rf value of a compound remains constant in all solvents.
Choose the most appropriate answer from the options given below :
13
Which of the following is correct structure of tyrosine?
14
Which of the following reaction is an example of ammonolysis?
15
A certain orbital has n = 4 and mL = $$-$$3. The number of radial nodes in this orbital is ____________. (Round off to the Nearest Integer).
16
15 mL of aqueous solution of Fe2+ in acidic medium completely reacted with 20 mL of 0.03 M aqueous Cr2O$$_7^{2 - }$$. The molarity of the Fe2+ solution is __________ $$\times$$ 10-2 M. (Round off to the Nearest Integer).
17
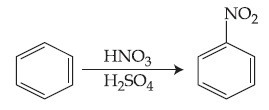
In the above reaction, 3.9 g of benzene on nitration gives 4.92 g of nitrobenzene. The percentage yield of nitrobenzene in the above reaction is ________%. (Round off to the Nearest Integer).
(Given atomic mass : C : 12.0 u, H : 1.0 u, O : 16.0 u, N : 14.0 u)
18
For a certain first order reaction 32% of the reactant is left after 570s. The rate constant of this reaction is _________ $$\times$$ 10$$-$$3 s$$-$$1. (Round off to the Nearest Integer). [Given : log102 = 0.301, ln10 = 2.303]
19
0.01 moles of a weak acid HA (Ka = 2.0 $$\times$$ 10$$-$$6) is dissolved in 1.0 L of 0.1 M HCl solution. The degree of dissociation of HA is __________ $$\times$$ 10$$-$$5 (Round off to the Nearest Integer).
[Neglect volume change on adding HA. Assume degree of dissociation <<1 ]
[Neglect volume change on adding HA. Assume degree of dissociation <<1 ]
20
The mole fraction of a solute in a 100 molal aqueous solution is ___________ $$\times$$ 10$$-$$2. (Round off to the Nearest Integer).
[Given : Atomic masses : H : 1.0 u, O : 16.0 u ]
[Given : Atomic masses : H : 1.0 u, O : 16.0 u ]
21
The standard enthalpies of formation of Al2O3 and CaO are $$-$$1675 kJ mol-1 and $$-$$635 kJ mol$$-$$1 respectively.
For the reaction
3CaO + 2Al $$ \to $$ 3Ca + Al2O3 the standard reaction enthalpy $$\Delta$$rH0 = _________ kJ.
(Round off to the Nearest Integer)
For the reaction
3CaO + 2Al $$ \to $$ 3Ca + Al2O3 the standard reaction enthalpy $$\Delta$$rH0 = _________ kJ.
(Round off to the Nearest Integer)
22
The oxygen dissolved in water exerts a partial pressure of 20 kPa in the vapour above water. The molar solubility of oxygen in water is __________ $$\times$$ 10$$-$$5 mol dm$$-$$3. (Round off to the Nearest Integer).
[Given : Henry's law constant = KH = 8.0 $$\times$$ 104 kPa for O2. Density of water with dissolved oxygen = 1.0 kg dm$$-$$3 ]
[Given : Henry's law constant = KH = 8.0 $$\times$$ 104 kPa for O2. Density of water with dissolved oxygen = 1.0 kg dm$$-$$3 ]
Mathematics
1
In a triangle PQR, the co-ordinates of the points P and Q are ($$-$$2, 4) and (4, $$-$$2) respectively. If the equation of the perpendicular bisector of PR is 2x $$-$$ y + 2 = 0, then the centre of the circumcircle of the $$\Delta$$PQR is :
2
The value of
$$\mathop {\lim }\limits_{x \to {0^ + }} {{{{\cos }^{ - 1}}(x - {{[x]}^2}).{{\sin }^{ - 1}}(x - {{[x]}^2})} \over {x - {x^3}}}$$, where [ x ] denotes the greatest integer $$ \le $$ x is :
$$\mathop {\lim }\limits_{x \to {0^ + }} {{{{\cos }^{ - 1}}(x - {{[x]}^2}).{{\sin }^{ - 1}}(x - {{[x]}^2})} \over {x - {x^3}}}$$, where [ x ] denotes the greatest integer $$ \le $$ x is :
3
Which of the following statements is correct for the function g($$\alpha$$) for $$\alpha$$ $$\in$$ R such that
$$g(\alpha ) = \int\limits_{{\pi \over 6}}^{{\pi \over 3}} {{{{{\sin }^\alpha }x} \over {{{\cos }^\alpha }x + {{\sin }^\alpha }x}}dx} $$
$$g(\alpha ) = \int\limits_{{\pi \over 6}}^{{\pi \over 3}} {{{{{\sin }^\alpha }x} \over {{{\cos }^\alpha }x + {{\sin }^\alpha }x}}dx} $$
4
Which of the following is true for y(x) that satisfies the differential equation
$${{dy} \over {dx}}$$ = xy $$-$$ 1 + x $$-$$ y; y(0) = 0 :
$${{dy} \over {dx}}$$ = xy $$-$$ 1 + x $$-$$ y; y(0) = 0 :
5
The sum of possible values of x for
tan$$-$$1(x + 1) + cot$$-$$1$$\left( {{1 \over {x - 1}}} \right)$$ = tan$$-$$1$$\left( {{8 \over {31}}} \right)$$ is :
tan$$-$$1(x + 1) + cot$$-$$1$$\left( {{1 \over {x - 1}}} \right)$$ = tan$$-$$1$$\left( {{8 \over {31}}} \right)$$ is :
6
The value of $$4 + {1 \over {5 + {1 \over {4 + {1 \over {5 + {1 \over {4 + ......\infty }}}}}}}}$$ is :
7
The inverse of $$y = {5^{\log x}}$$ is :
8
Two dies are rolled. If both dices have six faces numbered 1, 2, 3, 5, 7 and 11, then the probability that the sum of the numbers on the top faces is less than or equal to 8 is :
9
If the fourth term in the expansion of $${(x + {x^{{{\log }_2}x}})^7}$$ is 4480, then the value of x where x$$\in$$N is equal to :
10
The system of equations kx + y + z = 1, x + ky + z = k and x + y + zk = k2 has no solution if k is equal to :
11
In a school, there are three types of games to be played. Some of the students play two types of games, but none play all the three games. Which Venn diagrams can justify the above statement?
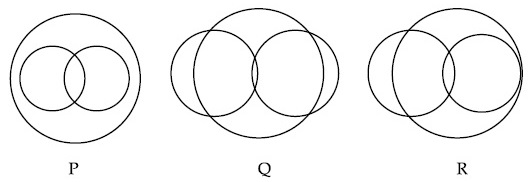

12
If cot$$-$$1($$\alpha$$) = cot$$-$$1 2 + cot$$-$$1 8 + cot$$-$$1 18 + cot$$-$$1 32 + ...... upto 100 terms, then $$\alpha$$ is :
13
Team 'A' consists of 7 boys and n girls and Team 'B' has 4 boys and 6 girls. If a total of 52 single matches can be arranged between these two teams when a boy plays against a boy and a girl plays against a girl, then n is equal to :
14
The area of the triangle with vertices A(z), B(iz) and C(z + iz) is :
15
If (2021)3762 is divided by 17, then the remainder is __________.
16
Let there be three independent events E1, E2 and E3. The probability that only E1 occurs is $$\alpha$$, only E2 occurs is $$\beta$$ and only E3 occurs is $$\gamma$$. Let 'p' denote the probability of none of events occurs that satisfies the equations
($$\alpha$$ $$-$$ 2$$\beta$$)p = $$\alpha$$$$\beta$$ and ($$\beta$$ $$-$$ 3$$\gamma$$)p = 2$$\beta$$$$\gamma$$. All the given probabilities are assumed to lie in the interval (0, 1).
Then, $$\frac{Probability\ of\ occurrence\ of\ E_{1}}{Probability\ of\ occurrence\ of\ E_{3}} $$ is equal to _____________.
($$\alpha$$ $$-$$ 2$$\beta$$)p = $$\alpha$$$$\beta$$ and ($$\beta$$ $$-$$ 3$$\gamma$$)p = 2$$\beta$$$$\gamma$$. All the given probabilities are assumed to lie in the interval (0, 1).
Then, $$\frac{Probability\ of\ occurrence\ of\ E_{1}}{Probability\ of\ occurrence\ of\ E_{3}} $$ is equal to _____________.
17
The maximum value of z in the following equation z = 6xy + y2, where 3x + 4y $$ \le $$ 100 and 4x + 3y $$ \le $$ 75 for x $$ \ge $$ 0 and y $$ \ge $$ 0 is __________.
18
If [ . ] represents the greatest integer function, then the value of
$$\left| {\int\limits_0^{\sqrt {{\pi \over 2}} } {\left[ {[{x^2}] - \cos x} \right]dx} } \right|$$ is ____________.
$$\left| {\int\limits_0^{\sqrt {{\pi \over 2}} } {\left[ {[{x^2}] - \cos x} \right]dx} } \right|$$ is ____________.
19
If $$f(x) = \sin \left( {{{\cos }^{ - 1}}\left( {{{1 - {2^{2x}}} \over {1 + {2^{2x}}}}} \right)} \right)$$ and its first derivative with respect to x is $$ - {b \over a}{\log _e}2$$ when x = 1, where a and b are integers, then the minimum value of | a2 $$-$$ b2 | is ____________ .
20
If the function $$f(x) = {{\cos (\sin x) - \cos x} \over {{x^4}}}$$ is continuous at each point in its domain and $$f(0) = {1 \over k}$$, then k is ____________.
Physics
1
A boy is rolling a 0.5 kg ball on the frictionless floor with the speed of 20 ms-1. The ball gets deflected by an obstacle on the way. After deflection it moves with 5% of its initial kinetic energy. What is the speed of the ball now?
2
A polyatomic ideal gas has 24 vibrational modes. What is the value of $$\gamma$$?
3
Two ideal polyatomic gases at temperatures T1 and T2 are mixed so that there is no loss of energy. If F1 and F2, m1 and m2, n1 and n2 be the degrees of freedom, masses, number of molecules of the first and second gas respectively, the temperature of mixture of these two gases is :
4
If an electron is moving in the nth orbit of the hydrogen atom, then its velocity (vn) for the nth orbit is given as :
5
Two identical metal wires of thermal conductivities K1 and K2 respectively are connected in series. The effective thermal conductivity of the combination is :
6
A triangular plate is shown. A force $$\overrightarrow F $$ = 4$$\widehat i$$ $$-$$ 3$$\widehat j$$ is applied at point P. The torque at point P with respect to point 'O' and 'Q' are :
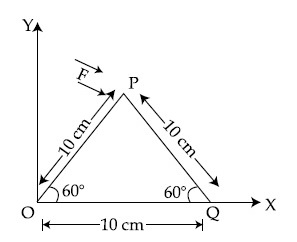

7
When two soap bubbles of radii a and b (b > a) coalesce, the radius of curvature of common surface is :
8
A car accelerates from rest at a constant rate $$\alpha$$ for some time after which it decelerates at a constant rate $$\beta$$ to come to rest. If the total time elapsed is t seconds, the total distance travelled is :
9
A mass M hangs on a massless rod of length l which rotates at a constant angular frequency. The mass M moves with steady speed in a circular path of constant radius. Assume that the system is in steady circular motion with constant angular velocity $$\omega$$. The angular momentum of M about point A is LA which lies in the positive z direction and the angular momentum of M about point B is LB. The correct statement for this system is :
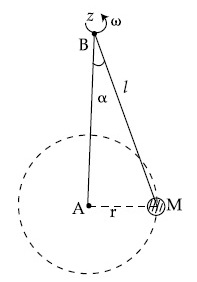

10
A solenoid of 1000 turns per metre has a core with relative permeability 500. Insulated windings of the solenoid carry an electric current of 5A. The magnetic flux density produced by the solenoid is : (permeability of free space = 4$$\pi$$ $$\times$$ 10$$-$$7 H/m)
11
The thickness at the centre of a plane convex lens is 3 mm and the diameter is 6 cm. If the speed of light in the material of the lens is 2 $$\times$$ 108 ms$$-$$1. The focal length of the lens is ____________.
12
For what value of displacement the kinetic energy and potential energy of a simple harmonic oscillation become equal ?
13
An AC current is given by I = I1 sin$$\omega$$t + I2 cos$$\omega$$t. A hot wire ammeter will give a reading :
14
A modern grand - prix racing car of mass m is travelling on a flat track in a circular arc of radius R with a speed v. If the coefficient of static friction between the tyres and the track is $$\mu$$s, then the magnitude of negative lift FL acting downwards on the car is : (Assume forces on the four tyres are identical and g = acceleration due to gravity)
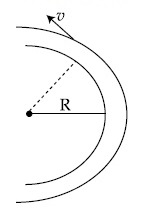

15
The vernier scale used for measurement has a positive zero error of 0.2 mm. If while taking a measurement it was noted that '0' on the vernier scale lies between 8.5 cm and 8.6 cm, vernier coincidence is 6, then the correct value of measurement is ___________ cm. (least count = 0.01 cm)
16
A current of 10A exists in a wire of cross-sectional area of 5 mm2 with a drift velocity of 2 $$\times$$ 10$$-$$3 ms$$-$$1. The number of free electrons in each cubic meter of the wire is ___________.
17
The output of the given combination gates represents :
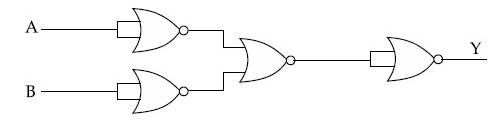

18
Which level of the single ionized carbon has the same energy as the ground state energy of hydrogen atom?
19
An electron of mass m and a photon have same energy E. The ratio of wavelength of electron to that of photon is : (c being the velocity of light)
20
The radius in kilometer to which the present radius of earth (R = 6400 km) to be compressed so that the escape velocity is increased 10 times is ___________.
21
The angular speed of truck wheel is increased from 900 rpm to 2460 rpm in 26 seconds. The number of revolutions by the truck engine during this time is _____________. (Assuming the acceleration to be uniform).
22
A parallel plate capacitor whose capacitance C is 14 pF is charged by a battery to a potential difference V = 12 V between its plates. The charging battery is now disconnected and a porcelin plate with k = 7 is inserted between the plates, then the plate would oscillate back and forth between the plates with a constant mechanical energy of _____________ pJ. (Assume no friction)
23
The following bodies,
(1) a ring
(2) a disc
(3) a solid cylinder
(4) a solid sphere,
of same mass 'm' and radius 'R' are allowed to roll down without slipping simultaneously from the top of the inclined plane. The body which will reach first at the bottom of the inclined plane is ___________. [Mark the body as per their respective numbering given in the question]

(1) a ring
(2) a disc
(3) a solid cylinder
(4) a solid sphere,
of same mass 'm' and radius 'R' are allowed to roll down without slipping simultaneously from the top of the inclined plane. The body which will reach first at the bottom of the inclined plane is ___________. [Mark the body as per their respective numbering given in the question]

24
Four identical rectangular plates with length, l = 2 cm and breadth, b = $${3 \over 2}$$ cm are arranged as shown in figure. The equivalent capacitance between A and C is $${{x{\varepsilon _0}} \over d}$$. The value of x is ______________. (Round off to the Nearest Integer)
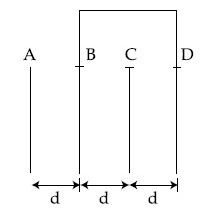

25
Consider two identical springs each of spring constant k and negligible mass compared to the mass M as shown. Fig. 1 shows one of them and Fig. 2 shows their series combination. The ratios of time period of oscillation of the two SHM is Tb/Ta = $$\sqrt x $$, where value of x is ___________. (Round off to the Nearest Integer)
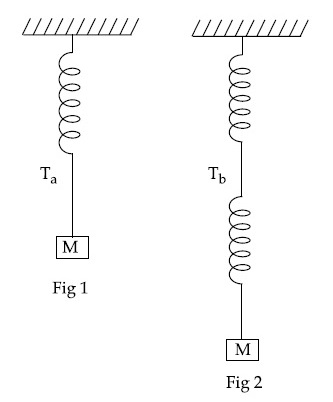

26
The equivalent resistance of series combination of two resistors is 's'. When they are connected in parallel, the equivalent resistance is 'p'. If s = np, then the minimum value for n is ____________. (Round off to the Nearest Integer)
27
Two blocks (m = 0.5 kg and M = 4.5 kg) are arranged on a horizontal frictionless table as shown in figure. The coefficient of static friction between the two blocks is $${3 \over 7}$$. Then the maximum horizontal force that can be applied on the larger block so that the blocks move together is ___________ N. (Round off to the Nearest Integer) [Take g as 9.8 ms$$-$$2]
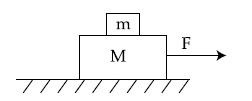

28
If 2.5 $$\times$$ 10$$-$$6 N average force is exerted by a light wave on a non-reflecting surface of 30 cm2 area during 40 minutes of time span, the energy flux of light just before it falls on the surface is ___________ W/cm2. (Round off to the Nearest Integer)
(Assume complete absorption and normal incidence conditions are there)
(Assume complete absorption and normal incidence conditions are there)