JEE Main 2014 (Offline)
Paper was held on
Sat, Apr 6, 2013 9:30 AM
Chemistry
1
Resistance of 0.2 M solution of an electrolyte is 50 $$\Omega$$. The specific conductance of the solution is 1.4 S m-1. The resistance of 0.5 M solution of the same electrolyte is 280 $$\Omega$$. The molar conductivity of 0.5 M solution of the electrolyte in S m2 mol-1 is :
2
Consider separate solutions of 0.500 M C2H5OH(aq), 0.100 M Mg3(PO4)2(aq), 0.250 M KBr(aq) and 0.125
M Na3PO4(aq) at 25oC. Which statement is true about these solutions, assuming all salts to be strong electrolytes?
3
For the estimation of nitrogen, 1.4 g of organic compound was digested by Kjeldahl method and the
evolved ammonia was absorbed in 60 mL of M/10 sulphuric acid. The unreacted acid required 20 ml of M/10
sodium hydroxide for complete neutralization. The percentage of nitrogen in the compound is:
4
In which of the following reactions H2O2 acts as a reducing agent?
1. H2O2 + 2H+ + 2e- $$\to$$ 2H2O
2. H2O2 - 2e- $$\to$$ O2 + 2H+
3. H2O2 + 2e- $$\to$$ 2OH-
4. H2O2 + 2OH- - 2e- $$\to$$ O2 + 2H2O
1. H2O2 + 2H+ + 2e- $$\to$$ 2H2O
2. H2O2 - 2e- $$\to$$ O2 + 2H+
3. H2O2 + 2e- $$\to$$ 2OH-
4. H2O2 + 2OH- - 2e- $$\to$$ O2 + 2H2O
5
For the reaction SO2 (g) + $${1 \over 2} O_2(g) \leftrightharpoons$$ SO3(g).
if KP = KC(RT)x where the symbols have usual meaning then the value of x is: (assuming ideality)
if KP = KC(RT)x where the symbols have usual meaning then the value of x is: (assuming ideality)
6
For complete combustion of ethanol, C2H5OH(l) + 3O2(g) $$\to$$ 2CO2(g) + 3H2O(l) the amount of heat
produced as measured in bomb calorimeter, is 1364.47 kJ mol–1 at 25oC. Assuming ideality the Enthalpy of combustion, $$\Delta _CH$$, for the reaction will be : (R = 8.314 kJ mol–1)
7
Given below are the half-cell reactions:
Mn2+ + 2e- $$\to$$ Mn; Eo = -1.18 V
2(Mn3+ + e- $$\to$$ Mn2+); Eo = +1.51 V
The Eo for 3Mn2+ $$\to$$ Mn + 2Mn3+ will be :
Mn2+ + 2e- $$\to$$ Mn; Eo = -1.18 V
2(Mn3+ + e- $$\to$$ Mn2+); Eo = +1.51 V
The Eo for 3Mn2+ $$\to$$ Mn + 2Mn3+ will be :
8
The ratio of masses of oxygen and nitrogen in a particular gaseous mixture is 1 : 4. The ratio of number of
their molecule is:
9
The major organic compound formed by the reaction of 1, 1, 1– trichloroethane with silver powder is:
10
Sodium phenoxide when heated with $$C{O_2}$$ under pressure at $${125^ \circ }C$$ yields a product which on acetylation products $$C.$$

The major product $$C$$ would be

The major product $$C$$ would be
11
Which one of the following bases is not present in DNA?
12
Considering the basic strength of amines in aqueous solution, which one has the smallest pKb value?
13
On heating an aliphatic primary amine with chloroform and ethanolic potassium hydroxide, the organic
compound formed is:
14
The most suitable reagent for the conversion of R - CH2 - OH $$\to$$ R - CHO is:
15
In the reaction,

the product C is:

the product C is:
16
In SN2 reactions, the correct order of reactivity for the following compounds:
CH3Cl, CH3CH 2Cl, (CH3)2CHCl and (CH3)3CCl is:
CH3Cl, CH3CH 2Cl, (CH3)2CHCl and (CH3)3CCl is:
17
The equation which is balanced and represents the correct product(s) is :
18
The octahedral complex of a metal ion M3+ with four monodentate ligands L1, L2, L3 and L4 absorb wavelengths in the region of red, green, yellow and blue, respectively. The increasing order of ligand strength of the four ligands is :
19
Which series of reactions correctly represents chemical relations related to iron and its compound?
20
The correct statement for the molecule, CsI3 is :
21
Which one of the following properties is not shown by NO?
22
For the non – stoichiometre reaction 2A + B $$\to$$ C + D, the following kinetic data were obtained in three
separate experiments, all at 298 K.
The rate law for the formation of C is:
| Initial Concentration (A) | Initial Concentration (B) | Initial rate of formation of C (mol L-1 s-1) |
|---|---|---|
| 0.1 M | 0.1 M | 1.2 x 10-3 |
| 0.1 M | 0.2 M | 1.2 x 10-3 |
| 0.2 M | 0.1 M | 2.4 x 10-3 |
23
The equivalent conductance of NaCl at concentration C and at infinite dilution are $${\lambda _C}$$ and $${\lambda _\infty }$$, respectively. The correct relationship between $${\lambda _C}$$ and $${\lambda _\infty }$$ is given as:
(where the constant B is positive)
24
The correct set of four quantum numbers for the valence elections of rubidium atom (Z= 37) is:
Mathematics
1
The variance of first 50 even natural numbers is
2
$$\mathop {\lim }\limits_{x \to 0} {{\sin \left( {\pi {{\cos }^2}x} \right)} \over {{x^2}}}$$ is equal to :
3
Let the population of rabbits surviving at time $$t$$ be governed by the differential equation $${{dp\left( t \right)} \over {dt}} = {1 \over 2}p\left( t \right) - 200.$$ If $$p(0)=100,$$ then $$p(t)$$ equals:
4
The integral $$\int\limits_0^\pi {\sqrt {1 + 4{{\sin }^2}{x \over 2} - 4\sin {x \over 2}{\mkern 1mu} } } dx$$ equals:
5
The area of the region described by
$$A = \left\{ {\left( {x,y} \right):{x^2} + {y^2} \le 1} \right.$$ and $$\left. {{y^2} \le 1 - x} \right\}$$ is :
$$A = \left\{ {\left( {x,y} \right):{x^2} + {y^2} \le 1} \right.$$ and $$\left. {{y^2} \le 1 - x} \right\}$$ is :
6
The integral $$\int {\left( {1 + x - {1 \over x}} \right){e^{x + {1 \over x}}}dx} $$ is equal to
7
If $$A$$ is a $$3 \times 3$$ non-singular matrix such that $$AA'=A'A$$ and
$$B = {A^{ - 1}}A',$$ then $$BB'$$ equals:
$$B = {A^{ - 1}}A',$$ then $$BB'$$ equals:
8
If $$\alpha ,\beta \ne 0,$$ and $$f\left( n \right) = {\alpha ^n} + {\beta ^n}$$ and
$$$\left| {\matrix{
3 & {1 + f\left( 1 \right)} & {1 + f\left( 2 \right)} \cr
{1 + f\left( 1 \right)} & {1 + f\left( 2 \right)} & {1 + f\left( 3 \right)} \cr
{1 + f\left( 2 \right)} & {1 + f\left( 3 \right)} & {1 + f\left( 4 \right)} \cr
} } \right|$$$
$$ = K{\left( {1 - \alpha } \right)^2}{\left( {1 - \beta } \right)^2}{\left( {\alpha - \beta } \right)^2},$$ then $$K$$ is equal to :
$$ = K{\left( {1 - \alpha } \right)^2}{\left( {1 - \beta } \right)^2}{\left( {\alpha - \beta } \right)^2},$$ then $$K$$ is equal to :
9
If $$x=-1$$ and $$x=2$$ are extreme points of $$f\left( x \right) = \alpha \,\log \left| x \right|+\beta {x^2} + x$$ then
10
If $$g$$ is the inverse of a function $$f$$ and $$f'\left( x \right) = {1 \over {1 + {x^5}}},$$ then $$g'\left( x \right)$$ is equal to:
11
Let $$A$$ and $$B$$ be two events such that $$P\left( {\overline {A \cup B} } \right) = {1 \over 6},\,P\left( { {A \cap B} } \right) = {1 \over 4}$$ and $$P\left( {\overline A } \right) = {1 \over 4},$$ where $$\overline A $$ stands for the complement of the event $$A$$. Then the events $$A$$ and $$B$$ are :
12
The locus of the foot of perpendicular drawn from the centre of the ellipse $${x^2} + 3{y^2} = 6$$ on any tangent to it is :
13
Let $$a, b, c$$ and $$d$$ be non-zero numbers. If the point of intersection of the lines $$4ax + 2ay + c = 0$$ and $$5bx + 2by + d = 0$$ lies in the fourth quadrant and is equidistant from the two axes then :
14
Let $$PS$$ be the median of the triangle with vertices $$P(2, 2)$$, $$Q(6, -1)$$ and $$R(7, 3)$$. The equation of the line passing through $$(1, -1)$$ band parallel to PS is :
15
Three positive numbers form an increasing G.P. If the middle term in this G.P. is doubled, the new numbers are in A.P. then the common ratio of the G.P. is :
16
Let $$\alpha $$ and $$\beta $$ be the roots of equation $$p{x^2} + qx + r = 0,$$ $$p \ne 0.$$ If $$p,\,q,\,r$$ in A.P. and $${1 \over \alpha } + {1 \over \beta } = 4,$$ then the value of $$\left| {\alpha - \beta } \right|$$ is :
17
If $$a \in R$$ and the equation $$ - 3{\left( {x - \left[ x \right]} \right)^2} + 2\left( {x - \left[ x \right]} \right) + {a^2} = 0$$ (where [$$x$$] denotes the greater integer $$ \le x$$) has no integral solution, then all possible values of a lie in the interval :
18
If z is a complex number such that $$\,\left| z \right| \ge 2\,$$, then the minimum value of $$\,\,\left| {z + {1 \over 2}} \right|$$ :
19
Let $$f_k\left( x \right) = {1 \over k}\left( {{{\sin }^k}x + {{\cos }^k}x} \right)$$ where $$x \in R$$ and $$k \ge \,1.$$
Then $${f_4}\left( x \right) - {f_6}\left( x \right)\,\,$$ equals :
Then $${f_4}\left( x \right) - {f_6}\left( x \right)\,\,$$ equals :
20
The angle between the lines whose direction cosines satisfy the equations $$l+m+n=0$$ and $${l^2} = {m^2} + {n^2}$$ is :
Physics
1
The current voltage relation of diode is given by $${\rm I} = \left( {{e^{100V/T}} - 1} \right)mA,$$ where the applied voltage $$V$$ is in volts and the temperature $$T$$ is in degree kelvin. If a student makes an error measuring $$ \pm 0.01\,V$$ while measuring the current of $$5$$ $$mA$$ at $$300$$ $$K,$$ what will be the error in the value of current on $$mA$$?
2
The forward biased diode connection is:
3
Match List - $$1$$ (Electromagnetic wave type ) with List - $$2$$ (Its association/application) and select the correct option from the choices given below the lists:
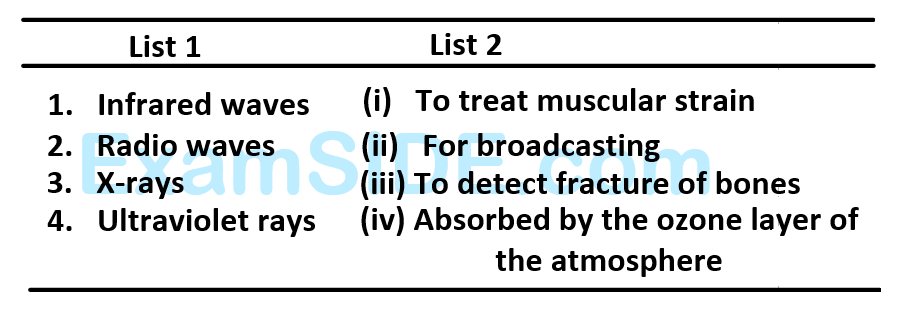

4
The radiation corresponding to $$3 \to 2$$ transition of hydrogen atom falls on a metal surface to produce photoelectrons. These electrons are made to enter a magnetic field $$3 \times {10^{ - 4}}\,T.$$ If the radius of the larger circular path followed by these electrons is $$10.0$$ $$mm$$, the work function of the metal is close to:
5
During the propagation of electromagnetic waves in a medium :
6
Hydrogen $$\left( {{}_1{H^1}} \right)$$, Deuterium $$\left( {{}_1{H^2}} \right)$$, singly ionised Helium $${\left( {{}_2H{e^4}} \right)^ + }$$ and doubly ionised lithium $${\left( {{}_3L{i^6}} \right)^{ + + }}$$ all have one electron around the nucleus. Consider an electron transition from $$n=2$$ to $$n=1.$$ If the wavelengths of emitted radiation are $${\lambda _1},{\lambda _2},{\lambda _3}$$ and $${\lambda _4}$$ respectively then approximately which one of the following is correct?
7
In the circuit shown here, the point $$'C'$$ is kept connected to point $$'A'$$ till the current flowing through the circuit becomes constant. Afterward, suddenly, point $$'C'$$ is disconnected from point $$'A'$$ and connected to point $$'B'$$ at time $$t=0.$$ Ratio of the voltage across resistance and the inductor at $$t=L/R$$ will be equal to :
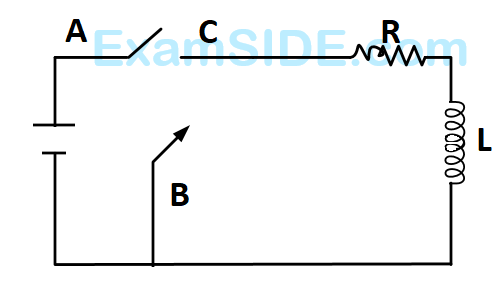

8
A green light is incident from the water to the air - water interface at the critical angle $$\left( \theta \right)$$. Select the correct statement.
9
A thin convex lens made from crown glass $$\left( {\mu = {3 \over 2}} \right)$$ has focal length $$f$$. When it is measured in two different liquids having refractive indices $${4 \over 3}$$ and $${5 \over 3},$$ it has the focal lengths $${f_1}$$ and $${f_2}$$ respectively. The correct relation between the focal lengths is :
10
Two beams, $$A$$ and $$B$$, of plane polarized light with mutually perpendicular planes of polarization are seen through a polaroid. From the position when the beam $$A$$ has maximum intensity (and beam $$B$$ has zero intensity), a rotation of polaroid through $${30^ \circ }$$ makes the two beams appear equally bright. If the initial intensities of the two beams are $${{\rm I}_A}$$ and $${{\rm I}_B}$$ respectively, then $${{{{\rm I}_A}} \over {{{\rm I}_B}}}$$ equals:
11
A conductor lies along the $$z$$-axis at $$ - 1.5 \le z < 1.5\,m$$ and carries a fixed current of $$10.0$$ $$A$$ in $$ - {\widehat a_z}$$ direction (see figure). For a field $$\overrightarrow B = 3.0 \times {10^{ - 4}}\,{e^{ - 0.2x}}\,\,{\widehat a_y}\,\,T,$$ find the power required to move the conductor at constant speed to $$x=2.0$$ $$m$$, $$y=0$$ $$m$$ in $$5 \times {10^{ - 3}}s.$$ Assume parallel motion along the $$x$$-axis.


12
The coercivity of a small magnet where the ferromagnet gets demagnetized is $$3 \times {10^3}\,A{m^{ - 1}}.$$ The current required to be passed in a solenoid of length $$10$$ $$cm$$ and number of turns $$100,$$ so that the magnet gets demagnetized when inside the solenoid, is :
13
In a large building, three are $$15$$ bulbs of $$40$$ $$W$$, $$5$$ bulbs of $$100$$ $$W$$, $$5$$ fans of $$80$$ $$W$$ and $$1$$ heater of $$1$$ $$kW.$$ The voltage of electric mains is $$220$$ $$V.$$ The minimum capacity of the main fuse of the building will be:
14
An open glass tube is immersed in mercury in such a way that a length of $$8$$ $$cm$$ extends above the mercury level. The open end of the tube is then closed and scaled and the tube is raised vertically up by additional $$46$$ $$cm$$. What will be length of the air column above mercury in the tube now? (Atmospheric pressure $$=76$$ $$cm$$ of $$Hg$$)
15
A parallel plate capacitor is made of two circular plates separated by a distance $$5$$ $$mm$$ and with a dielectric of dielectric constant $$2.2$$ between them. When the electric field in the dielectric is $$3 \times {10^4}\,V/m$$ the charge density of the positive plate will be close to:
16
Assume that an electric field $$\overrightarrow E = 30{x^2}\widehat i$$ exists in space. Then the potential difference $${V_A} - {V_O},$$ where $${V_O}$$ is the potential at the origin and $${V_A}$$ the potential at $$x=2$$ $$m$$ is :
17
A pipe of length $$85$$ $$cm$$ is closed from one end. Find the number of possible natural oscillations of air column in the pipe whose frequencies lie below $$1250$$ $$Hz$$. The velocity of sound in air is $$340$$ $$m/s$$.
18
A particle moves with simple harmonic motion in a straight line. In first $$\tau s,$$ after starting from rest it travels a distance $$a,$$ and in next $$\tau s$$ it travels $$2a,$$ in same direction, then:
19
One mole of a diatomic ideal gas undergoes a cyclic process $$ABC$$ as shown in figure. The process $$BC$$ is adiabatic. The temperatures at $$A, B$$ and $$C$$ are $$400$$ $$K$$, $$800$$ $$K$$ and $$600$$ $$K$$ respectively. Choose the correct statement :
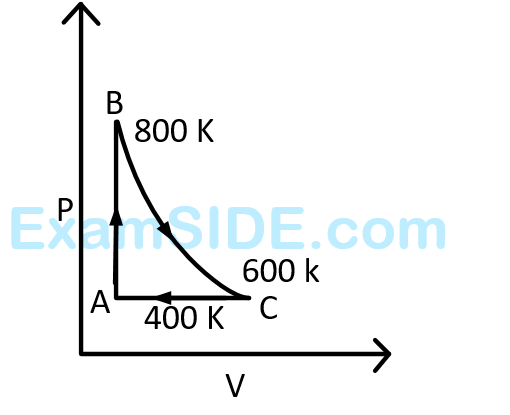

20
There is a circular tube in a vertical plane. Two liquids which do not mix and of densities $${d_1}$$ and $${d_2}$$ are filled in the tube. Each liquid subtends $${90^ \circ }$$ angle at center. Radius joining their interface makes an angle $$\alpha $$ with vertical. Radio $${{{d_1}} \over {{d_2}}}$$ is :
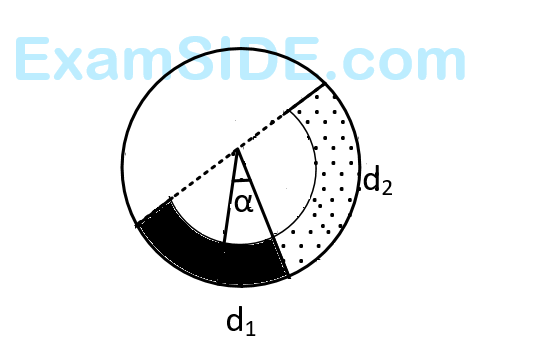

21
On heating water, bubbles being formed at the bottom of the vessel detach and rise. Take the bubbles to be spheres of radius $$R$$ and making a circular contact of radius $$r$$ with the bottom $$R$$ and making a circular contact of radius $$r$$ with the bottom of the vessel. If $$r < < R$$ and the surface tension of water is $$T,$$ value of $$r$$ just before bubbles detach is: (density of water is $${\rho _w}$$)
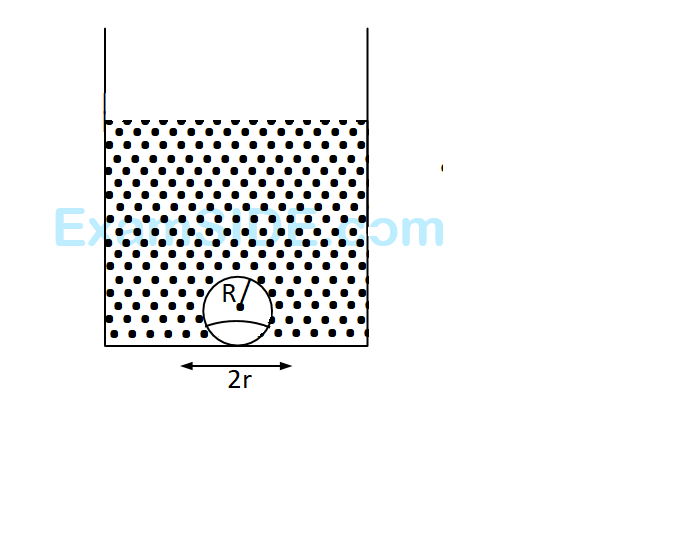

22
Three rods of Copper, Brass and Steel are welded together to form a $$Y$$ shaped structure. Area of cross - section of each rod $$ = 4c{m^2}.$$ End of copper rod is maintained at $${100^ \circ }C$$ where as ends of brass and steel are kept at $${0^ \circ }C$$. Lengths of the copper, brass and steel rods are $$46,$$ $$13$$ and $$12$$ $$cms$$ respectively. The rods are thermally insulated from surroundings excepts at ends. Thermal conductivities of copper, brass and steel are $$0.92, 0.26$$ and $$0.12$$ $$CGS$$ units respectively. Rate of heat flow through copper rod is:
23
The pressure that has to be applied to the ends of a steel wire of length $$10$$ $$cm$$ to keep its length constant when its temperature is raised by $${100^ \circ }C$$ is:
(For steel Young's modulus is $$2 \times {10^{11}}\,\,N{m^{ - 2}}$$ and coefficient of thermal expansion is $$1.1 \times {10^{ - 5}}\,{K^{ - 1}}$$ )
24
A mass $$'m'$$ is supported by a massless string wound around a uniform hollow cylinder of mass $$m$$ and radius $$R.$$ If the string does not slip on the cylinder, with what acceleration will the mass fall or release?
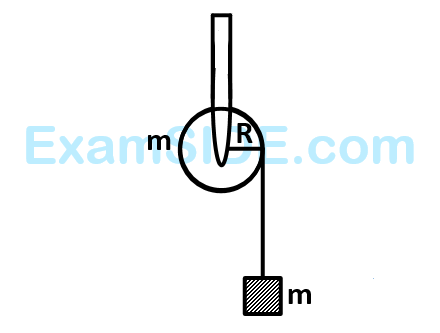

25
Four particles, each of mass $$M$$ and equidistant from each other, move along a circle of radius $$R$$ under the action of their mutual gravitational attraction. The speed of each particle is :
26
A bob of mass $$m$$ attached to an inextensible string of length $$l$$ is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed $$\omega \,rad/s$$ about the vertical. About the point of suspension:
27
When a rubber-band is stretched by a distance $$x$$, it exerts restoring force of magnitude $$F = ax + b{x^2}$$ where $$a$$ and $$b$$ are constants. The work done in stretching the unstretched rubber-band by $$L$$ is :
28
A block of mass $$m$$ is placed on a surface with a vertical cross section given by $$y = {{{x^3}} \over 6}.$$ If the coefficient of friction is $$0.5,$$ the maximum height above the ground at which the block can be placed without slipping is:
29
From a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the
particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation
between H, u and n is:
30
A student measured the length of a rod and wrote it as 3.50 cm. Which instrument did he use to measure it?