JEE Main 2021 (Online) 16th March Evening Shift
Paper was held on
Tue, Mar 16, 2021 9:30 AM
Chemistry
1
Match List - I with List - II :
The correct match is :
| List - I Test/Reagents/Observation(s) |
List - II Species detected |
||
|---|---|---|---|
| (a) | Lassaigne's Test | (i) | Carbon |
| (b) | Cu(II) oxide | (ii) | Sulphur |
| (c) | Silver nitrate | (iii) | N, S, P, and halogen |
| (d) | The sodium fusion extract gives black precipitate with acetic acid and lead acetate |
(iv) | Halogen Specifically |
The correct match is :
2
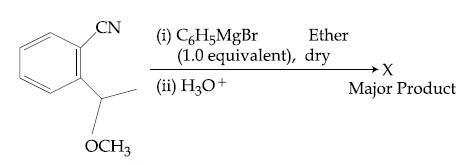
The structure of X is :
3
An unsaturated hydrocarbon X on ozonolysis gives A. Compound A when warmed with ammonical silver nitrate forms a bright silver mirror along the sides of the test tube. The unsaturated hydrocarbon X is :
4
The exact volumes of 1 M NaOH solution required to neutralise 50 mL of 1 M H3PO3 solution and 100 mL of 2 M H3PO2 solution, respectively, are :
5
The characteristics of elements X, Y and Z with atomic numbers, respectively, 33, 53 and 83 are :
6
Which of the following is least basic?
7
Ammonolysis of Alkyl halides followed by the treatment with NaOH solution can be used to prepare primary, secondary and tertiary amines. The purpose of NaOH in the reaction is :
8
The secondary structure of protein is stabilised by:
9
Fex2 and Fey3 are known when x and y are :
10
Identify the elements X and Y using the ionisation energy values given below :
| Ionization energy (kJ/mol) | ||
|---|---|---|
| 1$${st}$$ | 2$${nd}$$ | |
| X | 495 | 4563 |
| Y | 731 | 1450 |
11
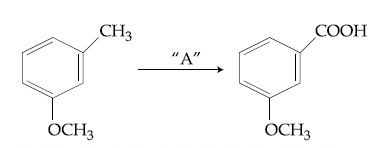
In the above reaction, the reagent ''A'' is :
12
Arrange the following metal complex/compounds in the increasing order of spin only magnetic moment. Presume all the three, high spin system.
(Atomic numbers Ce = 58, Gd = 64 and Eu = 63)
(a) (NH4)2[Ce(NO3)6]
(b) Gd(NO3)3 and
(c) Eu(NO3)3
(Atomic numbers Ce = 58, Gd = 64 and Eu = 63)
(a) (NH4)2[Ce(NO3)6]
(b) Gd(NO3)3 and
(c) Eu(NO3)3
13

Identify the reagent(s) 'A' and condition(s) for the reaction
14
Statement I : Sodium hydride can be used as an oxidising agent.
Statement II : The lone pair of electrons on nitrogen in pyridine makes it basic.
Choose the CORRECT answer from the options given below :
Statement II : The lone pair of electrons on nitrogen in pyridine makes it basic.
Choose the CORRECT answer from the options given below :
15
[Ti(H2O)6]3+ absorbs light of wavelength 498 nm during a d $$-$$ d transition. The octahedral splitting energy for the above complex is ____________ $$\times$$ 10$$-$$19 J. (Round off to the Nearest Integer). h = 6.626 $$\times$$ 10$$-$$34 Js; c = 3 $$\times$$ 108 ms$$-$$1
16
A 5.0 m mol dm$$-$$3 aqueous solution of KCl has a conductance of 0.55 mS when measured in a cell of cell constant 1.3 cm$$-$$1. The molar conductivity of this solution is ___________ mSm2 mol$$-$$1. (Round off to the Nearest Integer).
17
At 25$$^\circ$$C, 50 g of iron reacts with HCl to form FeCl2. The evolved hydrogen gas expands against a constant pressure of 1 bar. The work done by the gas during this expansion is _________ J. (Round off to the Nearest Integer).
[Given : R = 8.314 J mol$$-$$1 K$$-$$1. Assume, hydrogen is an ideal gas] [Atomic mass of Fe is 55.85 u]
[Given : R = 8.314 J mol$$-$$1 K$$-$$1. Assume, hydrogen is an ideal gas] [Atomic mass of Fe is 55.85 u]
18
The number of orbitals with n = 5, m1 = +2 is ___________. (Round off to the Nearest Integer).
19
A and B decompose via first order kinetics with half-lives 54.0 min and 18.0 min respectively. Starting from an equimolar non reactive mixture of A and B, the time taken for the concentration of A to become 16 times that of B is _________ min. (Round off to the Nearest Integer).
20
In Duma's method of estimation of nitrogen, 0.1840 g of an organic compound gave 30 mL of nitrogen collected at 287 K and 758 mm of Hg pressure. The percentage composition of nitrogen in the compound is __________. (Round off to the Nearest Integer). [Given : Aqueous tension at 287 K = 14 mm of Hg]
21
When 35 mL of 0.15 M lead nitrate solution is mixed with 20 mL of 0.12 M chromic sulphate solution, _________ $$\times$$ 10$$-$$5 moles of lead sulphate precipitate out. (Round off to the Nearest Integer).
22
Sulphurous acid (H2SO3) has Ka1 = 1.7 $$\times$$ 10$$-$$2 and Ka2 = 6.4 $$\times$$ 10$$-$$8. The pH of 0.588 M H2SO3 is __________. (Round off to the Nearest Integer).
23
At 363 K, the vapour pressure of A is 21 kPa and that of B is 18 kPa. One mole of A and 2 moles of B are mixed. Assuming that this solution is ideal, the vapour pressure of the mixture is ___________ kPa. (Round off to the Nearest Integer).
Mathematics
1
If y = y(x) is the solution of the differential equation
$${{dy} \over {dx}}$$ + (tan x) y = sin x, $$0 \le x \le {\pi \over 3}$$, with y(0) = 0, then $$y\left( {{\pi \over 4}} \right)$$ equal to :
$${{dy} \over {dx}}$$ + (tan x) y = sin x, $$0 \le x \le {\pi \over 3}$$, with y(0) = 0, then $$y\left( {{\pi \over 4}} \right)$$ equal to :
2
Let f be a real valued function, defined on R $$-$$ {$$-$$1, 1} and given by
f(x) = 3 loge $$\left| {{{x - 1} \over {x + 1}}} \right| - {2 \over {x - 1}}$$.
Then in which of the following intervals, function f(x) is increasing?
f(x) = 3 loge $$\left| {{{x - 1} \over {x + 1}}} \right| - {2 \over {x - 1}}$$.
Then in which of the following intervals, function f(x) is increasing?
3
Let $$\overrightarrow a $$ = $$\widehat i$$ + 2$$\widehat j$$ $$-$$ 3$$\widehat k$$ and $$\overrightarrow b = 2\widehat i$$ $$-$$ 3$$\widehat j$$ + 5$$\widehat k$$. If $$\overrightarrow r $$ $$\times$$ $$\overrightarrow a $$ = $$\overrightarrow b $$ $$\times$$ $$\overrightarrow r $$,
$$\overrightarrow r $$ . $$\left( {\alpha \widehat i + 2\widehat j + \widehat k} \right)$$ = 3 and $$\overrightarrow r \,.\,\left( {2\widehat i + 5\widehat j - \alpha \widehat k} \right)$$ = $$-$$1, $$\alpha$$ $$\in$$ R, then the
value of $$\alpha$$ + $${\left| {\overrightarrow r } \right|^2}$$ is equal to :
$$\overrightarrow r $$ . $$\left( {\alpha \widehat i + 2\widehat j + \widehat k} \right)$$ = 3 and $$\overrightarrow r \,.\,\left( {2\widehat i + 5\widehat j - \alpha \widehat k} \right)$$ = $$-$$1, $$\alpha$$ $$\in$$ R, then the
value of $$\alpha$$ + $${\left| {\overrightarrow r } \right|^2}$$ is equal to :
4
If the foot of the perpendicular from point (4, 3, 8) on the line $${L_1}:{{x - a} \over l} = {{y - 2} \over 3} = {{z - b} \over 4}$$, l $$\ne$$ 0 is (3, 5, 7), then the shortest distance between the line L1 and line $${L_2}:{{x - 2} \over 3} = {{y - 4} \over 4} = {{z - 5} \over 5}$$ is equal to :
5
Consider a rectangle ABCD having 5, 7, 6, 9 points in the interior of the line segments AB, CD, BC, DA respectively. Let $$\alpha$$ be the number of triangles having these points from different sides as vertices and $$\beta$$ be the number of quadrilaterals having these points from different sides as vertices. Then ($$\beta$$ $$-$$ $$\alpha$$) is equal to :
6
Let f : S $$ \to $$ S where S = (0, $$\infty $$) be a twice differentiable function such that f(x + 1) = xf(x). If g : S $$ \to $$ R be defined as g(x) = loge f(x), then the value of |g''(5) $$-$$ g''(1)| is equal to :
7
Consider the integral
$$I = \int_0^{10} {{{[x]{e^{[x]}}} \over {{e^{x - 1}}}}dx} $$,
where [x] denotes the greatest integer less than or equal to x. Then the value of I is equal to :
$$I = \int_0^{10} {{{[x]{e^{[x]}}} \over {{e^{x - 1}}}}dx} $$,
where [x] denotes the greatest integer less than or equal to x. Then the value of I is equal to :
8
Let C1 be the curve obtained by the solution of differential equation
$$2xy{{dy} \over {dx}} = {y^2} - {x^2},x > 0$$. Let the curve C2 be the
solution of $${{2xy} \over {{x^2} - {y^2}}} = {{dy} \over {dx}}$$. If both the curves pass through (1, 1), then the area enclosed by the curves C1 and C2 is equal to :
$$2xy{{dy} \over {dx}} = {y^2} - {x^2},x > 0$$. Let the curve C2 be the
solution of $${{2xy} \over {{x^2} - {y^2}}} = {{dy} \over {dx}}$$. If both the curves pass through (1, 1), then the area enclosed by the curves C1 and C2 is equal to :
9
Let P(x) = x2 + bx + c be a quadratic polynomial with real coefficients such that $$\int_0^1 {P(x)dx} $$ = 1 and P(x) leaves remainder 5 when it is divided by (x $$-$$ 2). Then the value of 9(b + c) is equal to :
10
Let A = {2, 3, 4, 5, ....., 30} and '$$ \simeq $$' be an equivalence relation on A $$\times$$ A, defined by (a, b) $$ \simeq $$ (c, d), if and only if ad = bc. Then the number of ordered pairs which satisfy this equivalence relation with ordered pair (4, 3) is equal to :
11
The least value of |z| where z is complex number which satisfies the inequality $$\exp \left( {{{(|z| + 3)(|z| - 1)} \over {||z| + 1|}}{{\log }_e}2} \right) \ge {\log _{\sqrt 2 }}|5\sqrt 7 + 9i|,i = \sqrt { - 1} $$, is equal to :
12
Let $$\alpha$$ $$\in$$ R be such that the function $$f(x) = \left\{ {\matrix{
{{{{{\cos }^{ - 1}}(1 - {{\{ x\} }^2}){{\sin }^{ - 1}}(1 - \{ x\} )} \over {\{ x\} - {{\{ x\} }^3}}},} & {x \ne 0} \cr
{\alpha ,} & {x = 0} \cr
} } \right.$$ is continuous at x = 0, where {x} = x $$-$$ [ x ] is the greatest integer less than or equal to x. Then :
13
Given that the inverse trigonometric functions take principal values only. Then, the number of real values of x which satisfy
$${\sin ^{ - 1}}\left( {{{3x} \over 5}} \right) + {\sin ^{ - 1}}\left( {{{4x} \over 5}} \right) = {\sin ^{ - 1}}x$$ is equal to :
$${\sin ^{ - 1}}\left( {{{3x} \over 5}} \right) + {\sin ^{ - 1}}\left( {{{4x} \over 5}} \right) = {\sin ^{ - 1}}x$$ is equal to :
14
Let the lengths of intercepts on x-axis and y-axis made by the circle
x2 + y2 + ax + 2ay + c = 0, (a < 0) be 2$${\sqrt 2 }$$ and 2$${\sqrt 5 }$$, respectively. Then the shortest distance from origin to a tangent to this circle which is perpendicular to the line x + 2y = 0, is equal to :
x2 + y2 + ax + 2ay + c = 0, (a < 0) be 2$${\sqrt 2 }$$ and 2$${\sqrt 5 }$$, respectively. Then the shortest distance from origin to a tangent to this circle which is perpendicular to the line x + 2y = 0, is equal to :
15
Let A($$-$$1, 1), B(3, 4) and C(2, 0) be given three points.
A line y = mx, m > 0, intersects lines AC and BC at point P and Q respectively. Let A1 and A2 be the areas of $$\Delta$$ABC and $$\Delta$$PQC respectively, such that A1 = 3A2, then the value of m is equal to :
A line y = mx, m > 0, intersects lines AC and BC at point P and Q respectively. Let A1 and A2 be the areas of $$\Delta$$ABC and $$\Delta$$PQC respectively, such that A1 = 3A2, then the value of m is equal to :
16
Let A denote the event that a 6-digit integer formed by 0, 1, 2, 3, 4, 5, 6 without repetitions, be divisible by 3. Then probability of event A is equal to :
17
The maximum value of
$$f(x) = \left| {\matrix{ {{{\sin }^2}x} & {1 + {{\cos }^2}x} & {\cos 2x} \cr {1 + {{\sin }^2}x} & {{{\cos }^2}x} & {\cos 2x} \cr {{{\sin }^2}x} & {{{\cos }^2}x} & {\sin 2x} \cr } } \right|,x \in R$$ is :
$$f(x) = \left| {\matrix{ {{{\sin }^2}x} & {1 + {{\cos }^2}x} & {\cos 2x} \cr {1 + {{\sin }^2}x} & {{{\cos }^2}x} & {\cos 2x} \cr {{{\sin }^2}x} & {{{\cos }^2}x} & {\sin 2x} \cr } } \right|,x \in R$$ is :
18
Let $${1 \over {16}}$$, a and b be in G.P. and $${1 \over a}$$, $${1 \over b}$$, 6 be in A.P., where a, b > 0. Then 72(a + b) is equal to ___________.
19
For real numbers $$\alpha$$, $$\beta$$, $$\gamma$$ and $$\delta $$, if
$$\int {{{({x^2} - 1) + {{\tan }^{ - 1}}\left( {{{{x^2} + 1} \over x}} \right)} \over {({x^4} + 3{x^2} + 1){{\tan }^{ - 1}}\left( {{{{x^2} + 1} \over x}} \right)}}dx} $$
$$ = \alpha {\log _e}\left( {{{\tan }^{ - 1}}\left( {{{{x^2} + 1} \over x}} \right)} \right) + \beta {\tan ^{ - 1}}\left( {{{\gamma ({x^2} + 1)} \over x}} \right) + \delta {\tan ^{ - 1}}\left( {{{{x^2} + 1} \over x}} \right) + C$$
where C is an arbitrary constant, then the value of 10($$\alpha$$ + $$\beta$$$$\gamma$$ + $$\delta$$) is equal to ______________.
$$\int {{{({x^2} - 1) + {{\tan }^{ - 1}}\left( {{{{x^2} + 1} \over x}} \right)} \over {({x^4} + 3{x^2} + 1){{\tan }^{ - 1}}\left( {{{{x^2} + 1} \over x}} \right)}}dx} $$
$$ = \alpha {\log _e}\left( {{{\tan }^{ - 1}}\left( {{{{x^2} + 1} \over x}} \right)} \right) + \beta {\tan ^{ - 1}}\left( {{{\gamma ({x^2} + 1)} \over x}} \right) + \delta {\tan ^{ - 1}}\left( {{{{x^2} + 1} \over x}} \right) + C$$
where C is an arbitrary constant, then the value of 10($$\alpha$$ + $$\beta$$$$\gamma$$ + $$\delta$$) is equal to ______________.
20
Let f : R $$ \to $$ R and g : R $$ \to $$ R be defined as
$$f(x) = \left\{ {\matrix{ {x + a,} & {x < 0} \cr {|x - 1|,} & {x \ge 0} \cr } } \right.$$ and
$$g(x) = \left\{ {\matrix{ {x + 1,} & {x < 0} \cr {{{(x - 1)}^2} + b,} & {x \ge 0} \cr } } \right.$$,
where a, b are non-negative real numbers. If (gof) (x) is continuous for all x $$\in$$ R, then a + b is equal to ____________.
$$f(x) = \left\{ {\matrix{ {x + a,} & {x < 0} \cr {|x - 1|,} & {x \ge 0} \cr } } \right.$$ and
$$g(x) = \left\{ {\matrix{ {x + 1,} & {x < 0} \cr {{{(x - 1)}^2} + b,} & {x \ge 0} \cr } } \right.$$,
where a, b are non-negative real numbers. If (gof) (x) is continuous for all x $$\in$$ R, then a + b is equal to ____________.
21
Consider the statistics of two sets of observations as follows :
If the variance of the combined set of these two observations is $${{17} \over 9}$$, then the value of n is equal to ___________.
| Size | Mean | Variance | |
|---|---|---|---|
| Observation I | 10 | 2 | 2 |
| Observation II | n | 3 | 1 |
If the variance of the combined set of these two observations is $${{17} \over 9}$$, then the value of n is equal to ___________.
22
Let $$A = \left[ {\matrix{
{{a_1}} \cr
{{a_2}} \cr
} } \right]$$ and $$B = \left[ {\matrix{
{{b_1}} \cr
{{b_2}} \cr
} } \right]$$ be two 2 $$\times$$ 1 matrices with real entries such that A = XB, where
$$X = {1 \over {\sqrt 3 }}\left[ {\matrix{ 1 & { - 1} \cr 1 & k \cr } } \right]$$, and k$$\in$$R.
If $$a_1^2$$ + $$a_2^2$$ = $${2 \over 3}$$(b$$_1^2$$ + b$$_2^2$$) and (k2 + 1) b$$_2^2$$ $$\ne$$ $$-$$2b1b2, then the value of k is __________.
$$X = {1 \over {\sqrt 3 }}\left[ {\matrix{ 1 & { - 1} \cr 1 & k \cr } } \right]$$, and k$$\in$$R.
If $$a_1^2$$ + $$a_2^2$$ = $${2 \over 3}$$(b$$_1^2$$ + b$$_2^2$$) and (k2 + 1) b$$_2^2$$ $$\ne$$ $$-$$2b1b2, then the value of k is __________.
Physics
1
What will be the nature of flow of water from a circular tap, when its flow rate increased from 0.18 L/min to 0.48 L/min? The radius of the tap and viscosity of water are 0.5 cm and 10$$-$$3 Pa s, respectively. (Density of water : 103 kg/m3)
2
The refractive index of a converging lens is 1.4. What will be the focal length of this lens if it is placed in a medium of same refractive index? Assume the radii of curvature of the faces of lens are R1 and R2 respectively.
3
The following logic gate is equivalent to :


4
Statement I : A cyclist is moving on an unbanked road with a speed of 7 kmh$$-$$1 and takes a sharp circular turn along a path of radius of 2m without reducing the speed. The static friction coefficient is 0.2. The cyclist will not slip and pass the curve. (g = 9.8 m/s2)
Statement II : If the road is banked at an angle of 45$$^\circ$$, cyclist can cross the curve of 2m radius with the speed of 18.5 kmh$$-$$1 without slipping.
In the light of the above statements, choose the correct answer from the options given below.
Statement II : If the road is banked at an angle of 45$$^\circ$$, cyclist can cross the curve of 2m radius with the speed of 18.5 kmh$$-$$1 without slipping.
In the light of the above statements, choose the correct answer from the options given below.
5
A large block of wood of mass M = 5.99 kg is hanging from two long massless cords. A bullet of mass m = 10 g is fired into the block and gets embedded in it. The (block + bullet) then swing upwards, their centre of mass rising a vertical distance h = 9.8 cm before the (block + bullet) pendulum comes momentarily to rest at the end of its arc. The speed of the bullet just before collision is :
(take g = 9.8 ms-2)
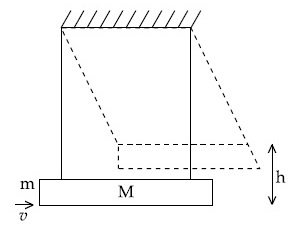
(take g = 9.8 ms-2)

6
A mosquito is moving with a velocity $$\overrightarrow v = 0.5{t^2}\widehat i + 3t\widehat j + 9\widehat k$$ m/s and accelerating in uniform conditions. What will be the direction of mosquito after 2 s?
7
Red light differs from blue light as they have :
8
The de-Broglie wavelength associated with an electron and a proton were calculated by accelerating them through same potential of 100 V. What should nearly be the ratio of their wavelengths? (mp = 1.00727u me = 0.00055u)
9
Calculate the value of mean free path ($$\lambda$$) for oxygen molecules at temperature 27$$^\circ$$C and pressure 1.01 $$\times$$ 105 Pa. Assume the molecular diameter 0.3 nm and the gas is ideal. (k = 1.38 $$\times$$ 10$$-$$23 JK$$-$$1)
10
A charge Q is moving $$\overrightarrow {dl} $$ distance in the magnetic field $$\overrightarrow {B} $$. Find the value of work done by $$\overrightarrow {B} $$.
11
In order to determine the Young's Modulus of a wire of radius 0.2 cm (measured using a scale of least count = 0.001 cm) and length 1m (measured using a scale of least count = 1 mm), a weight of mass 1 kg (measured using a scale of least count = 1 g) was hanged to get the elongation of 0.5 cm (measured using a scale of least count 0.001 cm). What will be the fractional error in the value of Young's Modulus determined by this experiment?
12
A resistor develops 500 J of thermal energy in 20 s when a current of 1.5A is passed through it. If the current is increased from 1.5A to 3A, what will be the energy developed in 20 s.
13
Find out the surface charge density at the intersection of point x = 3 m plane and x-axis, in the region of uniform line charge of 8 nC/m lying along the z-axis in free space.
14
The magnetic field in a region is given by $$\overrightarrow B = {B_o}\left( {{x \over a}} \right)\widehat k$$. A square loop of side d is placed with its edges along the x and y axes. The loop is moved with a constant velocity $$\overrightarrow v $$ = v0$$\widehat i$$. The emf induced in the loop is :
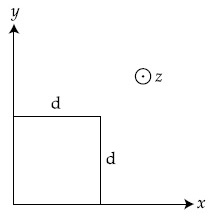

15
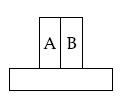
A bimetallic strip consists of metals A and B. It is mounted rigidly as shown. The metal A has higher coefficient of expansion compared to that of metal B. When the bimetallic strip is placed in a cold bath, it will :

16
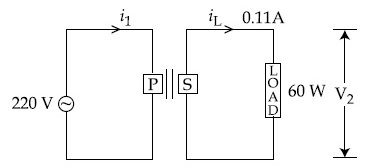
For the given circuit, comment on the type of transformer used.

17
A solid disc of radius 'a' and mass 'm' rolls down without slipping on an inclined plane making an angle $$\theta$$ with the horizontal. The acceleration of the disc will be $${2 \over b}$$g sin$$\theta$$ where b is ____________. (Round off to the Nearest Integer) (g = acceleration due to gravity, $$\theta$$ = angle as shown in figure)


18
The energy dissipated by a resistor is 10 mJ in 1 s when an electric current of 2 mA flows through it. The resistance is ___________$$\Omega$$. (Round off to the Nearest Integer)
19
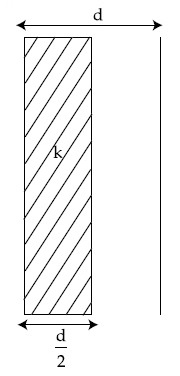
In a parallel plate capacitor set up, the plate area of capacitor is 2 m2 and the plates are separated by 1 m. If the space between the plates are filled with a dielectric material of thickness 0.5 m and area 2 m2 (see fig.) the capacitance of the set-up will be __________$$\varepsilon $$o. (Dielectric constant of the material = 3.2) (Round off to the Nearest Integer)

20
If one wants to remove all the mass of the earth to infinity in order to break it up completely.
The amount of energy that needs to be supplied will be $${x \over 5}{{G{M^2}} \over R}$$ where x is __________ (Round off to the Nearest Integer) (M is the mass of earth, R is the radius of earth, G is the gravitational constant)
The amount of energy that needs to be supplied will be $${x \over 5}{{G{M^2}} \over R}$$ where x is __________ (Round off to the Nearest Integer) (M is the mass of earth, R is the radius of earth, G is the gravitational constant)
21
A body of mass 2 kg moves under a force of $$\left( {2\widehat i + 3\widehat j + 5\widehat k} \right)$$N. It starts from rest and was at the origin initially. After 4s, its new coordinates are (8, b, 20). The value of b is _____________. (Round off to the Nearest Integer)
22
A closed organ pipe of length L and an open organ pipe contain gases of densities $$\rho$$1 and $$\rho$$2 respectively. The compressibility of gases are equal in both the pipes. Both the pipes are vibrating in their first overtone with same frequency. The length of the open pipe is $${x \over 3}L\sqrt {{{{\rho _1}} \over {{\rho _2}}}} $$ where x is ___________. (Round off to the Nearest Integer)
23
A swimmer can swim with velocity of 12 km/h in still water. Water flowing in a river has velocity 6 km/h. The direction with respect to the direction of flow of river water he should swim in order to reach the point on the other bank just opposite to his starting point is ____________$$^\circ$$. (Round off to the Nearest Integer) (Find the angle in degrees)
24
A deviation of 2$$^\circ$$ is produced in the yellow ray when prism of crown and flint glass are achromatically combined. Taking dispersive powers of crown and flint glass as 0.02 and 0.03 respectively and refractive index for yellow light for these glasses are 1.5 and 1.6 respectively. The refracting angles for crown glass prism will be ____________$$^\circ$$ (in degree). (Round off to the Nearest Integer)
25
A force $$\overrightarrow F $$ = $${4\widehat i + 3\widehat j + 4\widehat k}$$ is applied on an intersection point of x = 2 plane and x-axis. The magnitude of torque of this force about a point (2, 3, 4) is ___________. (Round off to the Nearest Integer)