JEE Main 2020 (Online) 6th September Morning Slot
Paper was held on
Sun, Sep 6, 2020 3:30 AM
Chemistry
1
The number of Cl = O bonds in perchloric acid
is, "________".
2
The elevation of boiling point of 0.10 m
aqueous CrCl3.xNH3 solution is two times that
of 0.05 m aqueous CaCl2 solution. The value of
x is ______.
[Assume 100% ionisation of the complex and CaCl2, coordination number of Cr as 6, and that all NH3 molecules are present inside the coordination sphere]
[Assume 100% ionisation of the complex and CaCl2, coordination number of Cr as 6, and that all NH3 molecules are present inside the coordination sphere]
3
Potassium chlorate is prepared by the
electrolysis of KCl in basic solution
6OH- + Cl- $$ \to $$ ClO3- + 3H2O + 6e-
If only 60% of the current is utilized in the reaction, the time (rounded to the nearest hour) required to produce 10 g of KClO3 using a current of 2 A is_________.
(Given : F = 96,500 C mol–1; molar mass of KCIO3 = 122 g mol–1)
6OH- + Cl- $$ \to $$ ClO3- + 3H2O + 6e-
If only 60% of the current is utilized in the reaction, the time (rounded to the nearest hour) required to produce 10 g of KClO3 using a current of 2 A is_________.
(Given : F = 96,500 C mol–1; molar mass of KCIO3 = 122 g mol–1)
4
In an estimation of bromine by Carius method,
1.6 g of an organic compound gave 1.88 g of
AgBr. The mass percentage of bromine in the
compound is _______.
(Atomic mass, Ag = 108, Br = 80 g mol–1)
(Atomic mass, Ag = 108, Br = 80 g mol–1)
5
The set that contains atomic numbers of only
transition elements, is :
6
Consider the following reactions

'A' is :

'A' is :
7
The variation of equilibrium constant with
temperature is given below :
The values of $$\Delta $$Ho, $$\Delta $$Go at
T1 and $$\Delta $$Go at T2 (in kJ mol–1) respectively, are close to :
[Use R = 8.314 J K–1 mol–1]
| Temperature | Equilibrium Constant |
|---|---|
| T1 = 25oC | K1 = 10 |
| T2 = 100oC | K2 = 100 |
The values of $$\Delta $$Ho, $$\Delta $$Go at
T1 and $$\Delta $$Go at T2 (in kJ mol–1) respectively, are close to :
[Use R = 8.314 J K–1 mol–1]
8
Consider the following reactions
A $$ \to $$ P1 ; B $$ \to $$ P2 ; C $$ \to $$ P3 ; D $$ \to $$ P4,
The order of the above reactions are a, b, c, and d, respectively. The following graph is obtained when log[rate] vs. log[conc.] are plotted
Among the following, the correct sequence for the order of the reactions is :
A $$ \to $$ P1 ; B $$ \to $$ P2 ; C $$ \to $$ P3 ; D $$ \to $$ P4,
The order of the above reactions are a, b, c, and d, respectively. The following graph is obtained when log[rate] vs. log[conc.] are plotted

Among the following, the correct sequence for the order of the reactions is :
9
The correct statement with respect to
dinitrogen is :
10
The major product obtained from the following
reaction is :


11
Which of the following compounds shows
geometrical isomerism?
12
The lanthanoid that does NOT show +4 oxidation
state is :
13
The major products of the following reaction are :


14
The major product of the following reaction is :


15
The species that has a spin-only magnetic
moment of 5.9 BM, is :
(Td = tetrahedral)
(Td = tetrahedral)
16
Arrange the following solutions in the
decreasing order of pOH :
(A) 0.01 M HCl
(B) 0.01 M NaOH
(C) 0.01 M CH3COONa
(D) 0.01 M NaCl
(A) 0.01 M HCl
(B) 0.01 M NaOH
(C) 0.01 M CH3COONa
(D) 0.01 M NaCl
17
For the reaction
Fe2N(s) + $${3 \over 2}$$H2(g) ⇌ 2Fe(s) + NH3(g)
Fe2N(s) + $${3 \over 2}$$H2(g) ⇌ 2Fe(s) + NH3(g)
18
A solution of two components containing
n1 moles of the 1st component and n2 moles of
the 2nd component is prepared. M1 and M2 are
the molecular weights of component 1 and 2
respectively. If d is the density of the solution
in g mL–1, C2 is the molarity and x2 is the mole
fraction of the 2nd component, then C2 can be
expressed as :
19
The increasing order of pKb values of the
following compounds is :


Mathematics
1
The area (in sq. units) of the region
A = {(x, y) : |x| + |y| $$ \le $$ 1, 2y2 $$ \ge $$ |x|}
A = {(x, y) : |x| + |y| $$ \le $$ 1, 2y2 $$ \ge $$ |x|}
2
The general solution of the differential equation
$$\sqrt {1 + {x^2} + {y^2} + {x^2}{y^2}} $$ + xy$${{dy} \over {dx}}$$ = 0 is :
(where C is a constant of integration)
$$\sqrt {1 + {x^2} + {y^2} + {x^2}{y^2}} $$ + xy$${{dy} \over {dx}}$$ = 0 is :
(where C is a constant of integration)
3
The region represented by
{z = x + iy $$ \in $$ C : |z| – Re(z) $$ \le $$ 1} is also given by the
inequality : {z = x + iy $$ \in $$ C : |z| – Re(z) $$ \le $$ 1}
{z = x + iy $$ \in $$ C : |z| – Re(z) $$ \le $$ 1} is also given by the
inequality : {z = x + iy $$ \in $$ C : |z| – Re(z) $$ \le $$ 1}
4
Let a , b, c , d and p be any non zero distinct real numbers such that
(a2 + b2 + c2)p2 – 2(ab + bc + cd)p + (b2 + c2 + d2) = 0. Then :
(a2 + b2 + c2)p2 – 2(ab + bc + cd)p + (b2 + c2 + d2) = 0. Then :
5
$$\mathop {\lim }\limits_{x \to 1} \left( {{{\int\limits_0^{{{\left( {x - 1} \right)}^2}} {t\cos \left( {{t^2}} \right)dt} } \over {\left( {x - 1} \right)\sin \left( {x - 1} \right)}}} \right)$$
6
Set A has m elements and set B has n elements. If the total number of subsets of A is 112 more
than the total number of subsets of B, then the value of m.n is ______.
7
Let f : R $$ \to $$ R be defined as
$$f\left( x \right) = \left\{ {\matrix{ {{x^5}\sin \left( {{1 \over x}} \right) + 5{x^2},} & {x < 0} \cr {0,} & {x = 0} \cr {{x^5}\cos \left( {{1 \over x}} \right) + \lambda {x^2},} & {x > 0} \cr } } \right.$$
The value of $$\lambda $$ for which f ''(0) exists, is _______.
$$f\left( x \right) = \left\{ {\matrix{ {{x^5}\sin \left( {{1 \over x}} \right) + 5{x^2},} & {x < 0} \cr {0,} & {x = 0} \cr {{x^5}\cos \left( {{1 \over x}} \right) + \lambda {x^2},} & {x > 0} \cr } } \right.$$
The value of $$\lambda $$ for which f ''(0) exists, is _______.
8
If $$\overrightarrow a $$
and $$\overrightarrow b $$
are unit vectors, then the greatest value of
$$\sqrt 3 \left| {\overrightarrow a + \overrightarrow b } \right| + \left| {\overrightarrow a - \overrightarrow b } \right|$$ is_____.
$$\sqrt 3 \left| {\overrightarrow a + \overrightarrow b } \right| + \left| {\overrightarrow a - \overrightarrow b } \right|$$ is_____.
9
If I1 = $$\int\limits_0^1 {{{\left( {1 - {x^{50}}} \right)}^{100}}} dx$$ and
I2 = $$\int\limits_0^1 {{{\left( {1 - {x^{50}}} \right)}^{101}}} dx$$ such
that I2 = $$\alpha $$I1 then $$\alpha $$ equals to :
I2 = $$\int\limits_0^1 {{{\left( {1 - {x^{50}}} \right)}^{101}}} dx$$ such
that I2 = $$\alpha $$I1 then $$\alpha $$ equals to :
10
The position of a moving car at time t is
given by f(t) = at2 + bt + c, t > 0, where a, b and c are real numbers greater than 1. Then the average speed of the car over the time interval [t1 , t2 ] is attained at the point :
given by f(t) = at2 + bt + c, t > 0, where a, b and c are real numbers greater than 1. Then the average speed of the car over the time interval [t1 , t2 ] is attained at the point :
11
If $$\alpha $$ and $$\beta $$ be two roots of the equation
x2 – 64x + 256 = 0. Then the value of
$${\left( {{{{\alpha ^3}} \over {{\beta ^5}}}} \right)^{1/8}} + {\left( {{{{\beta ^3}} \over {{\alpha ^5}}}} \right)^{1/8}}$$ is :
x2 – 64x + 256 = 0. Then the value of
$${\left( {{{{\alpha ^3}} \over {{\beta ^5}}}} \right)^{1/8}} + {\left( {{{{\beta ^3}} \over {{\alpha ^5}}}} \right)^{1/8}}$$ is :
12
If $$\sum\limits_{i = 1}^n {\left( {{x_i} - a} \right)} = n$$ and $$\sum\limits_{i = 1}^n {{{\left( {{x_i} - a} \right)}^2}} = na$$
(n, a > 1) then the standard deviation of n
observations x1 , x2 , ..., xn is :
(n, a > 1) then the standard deviation of n
observations x1 , x2 , ..., xn is :
13
If {p} denotes the fractional part of the number p, then
$$\left\{ {{{{3^{200}}} \over 8}} \right\}$$, is equal to :
$$\left\{ {{{{3^{200}}} \over 8}} \right\}$$, is equal to :
14
If f(x + y) = f(x)f(y) and $$\sum\limits_{x = 1}^\infty {f\left( x \right)} = 2$$ , x, y $$ \in $$ N, where N is the set of all natural number, then the
value of
$${{f\left( 4 \right)} \over {f\left( 2 \right)}}$$ is :
15
Out of 11 consecutive natural numbers if three numbers are selected at random (without repetition), then the probability that they are in A.P. with positive common difference, is :
16
A ray of light coming from the point (2, $$2\sqrt 3 $$) is incident at an angle 30o on the line x = 1 at the
point A. The ray gets reflected on the line x = 1 and meets x-axis at the point B. Then, the line AB
passes through the point :
17
The values of $$\lambda $$ and $$\mu $$ for which the system of linear equations
x + y + z = 2
x + 2y + 3z = 5
x + 3y + $$\lambda $$z = $$\mu $$
has infinitely many solutions are, respectively:
x + y + z = 2
x + 2y + 3z = 5
x + 3y + $$\lambda $$z = $$\mu $$
has infinitely many solutions are, respectively:
18
Let m and M be respectively the minimum and maximum values of
$$\left| {\matrix{ {{{\cos }^2}x} & {1 + {{\sin }^2}x} & {\sin 2x} \cr {1 + {{\cos }^2}x} & {{{\sin }^2}x} & {\sin 2x} \cr {{{\cos }^2}x} & {{{\sin }^2}x} & {1 + \sin 2x} \cr } } \right|$$
Then the ordered pair (m, M) is equal to :
$$\left| {\matrix{ {{{\cos }^2}x} & {1 + {{\sin }^2}x} & {\sin 2x} \cr {1 + {{\cos }^2}x} & {{{\sin }^2}x} & {\sin 2x} \cr {{{\cos }^2}x} & {{{\sin }^2}x} & {1 + \sin 2x} \cr } } \right|$$
Then the ordered pair (m, M) is equal to :
19
Two families with three members each and one family with four members are to be seated in a row.
In how many ways can they be seated so that the same family members are not separated?
Physics
1
Identify the correct output signal Y in the given combination of gates (as shown) for the given
inputs A and B.


2
A particle of charge q and mass m is moving with a velocity $$ - v\widehat i$$ (v $$ \ne $$ 0) towards a large screen
placed in the Y - Z plane at a distance d. If there is a magnetic field $$\overrightarrow B = {B_0}\widehat k$$
, the maximum value of v
for which the particle will not hit the screen is :
3
Two bodies of the same mass are moving with the same speed, but in different directions in a
plane. They have a completely inelastic collision and move together thereafter with a final speed
which is half of their initial speed. The angle between the initial velocities of the two bodies (in
degree) is ________.
4
Molecules of an ideal gas are known to have three translational degrees of freedom and two
rotational degrees of freedom.The gas is maintained at a temperature of T. The total internal
energy, U of a mole of this gas, and the value of
$$\gamma \left( { = {{{C_p}} \over {{C_v}}}} \right)$$ are given, respectively by:
$$\gamma \left( { = {{{C_p}} \over {{C_v}}}} \right)$$ are given, respectively by:
5
An object of mass m is suspended at the end of a massless wire of length L and area of crosssection A. Young modulus of the material of the wire is Y. If the mass is pulled down slightly its
frequency of oscillation along the vertical direction is :
6
A point like object is placed at a distance of 1 m in front of a convex lens of focal length 0.5 m. A
plane mirror is placed at a distance of 2 m behind the lens. The position and nature of the final
image formed by the system is :
7
An insect is at the bottom of a hemispherical ditch of radius 1 m. It crawls up the ditch but starts
slipping after it is at height h from the bottom. If the coefficient of friction between the ground and
the insect is 0.75, then h is :
(g = 10 ms–2)
(g = 10 ms–2)
8
In the figure below, P and Q are two equally intense coherent sources emitting radiation of
wavelength 20 m. The separation between P and Q is 5 m and the phase of P is ahead of that of Q
by 90o. A, B and C are three distinct points of observation, each equidistant from the midpoint of
PQ. The intensities of radiation at A, B, C will be in the ratio :


9
A clock has a continuously moving second's hand of 0.1 m length. The average acceleration of the
tip of the hand (in units of ms–2) is of the order of :
10
Charges Q1
and Q2
are at points A and B of a right angle triangle OAB (see figure). The resultant
electric field at point O is perpendicular to the hypotenuse, then
$${{{Q_1}} \over {{Q_2}}}$$ is proportional to :
$${{{Q_1}} \over {{Q_2}}}$$ is proportional to :

11
An electron is moving along +x direction with a velocity of 6 $$ \times $$ 106
ms–1. It enters a region of uniform
electric field of 300 V/cm pointing along +y direction. The magnitude and direction of the magnetic
field set up in this region such that the electron keeps moving along the x direction will be :
12
Shown in the figure is a hollow icecream cone (it is open at the top). If its mass is M, radius of its
top, R and height, H, then its moment of inertia about its axis is :
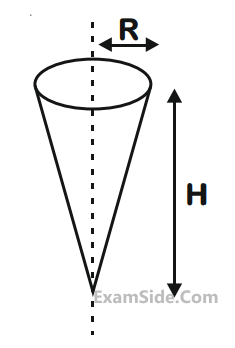

13
You are given that Mass of $${}_3^7Li$$ = 7.0160u,
Mass of $${}_2^4He$$ = 4.0026u
and Mass of $${}_1^1H$$ = 1.0079u.
When 20 g of $${}_3^7Li$$ is converted into $${}_2^4He$$ by proton capture, the energy liberated, (in kWh), is :
[Mass of nucleon = 1 GeV/c2]
Mass of $${}_2^4He$$ = 4.0026u
and Mass of $${}_1^1H$$ = 1.0079u.
When 20 g of $${}_3^7Li$$ is converted into $${}_2^4He$$ by proton capture, the energy liberated, (in kWh), is :
[Mass of nucleon = 1 GeV/c2]
14
If the potential energy between two molecules is given by
U = $$ - {A \over {{r^6}}} + {B \over {{r^{12}}}}$$,
then at equilibrium, separation between molecules, and the potential energy are :
U = $$ - {A \over {{r^6}}} + {B \over {{r^{12}}}}$$,
then at equilibrium, separation between molecules, and the potential energy are :
15
A satellite is in an elliptical orbit around a planet P. It is observed that the velocity of the satellite
when it is farthest from the planet is 6 times less than that when it is closest to the planet. The
ratio of distances between the satellite and the planet at closest and farthest points is:
16
For the given input voltage waveform Vin(t), the output voltage waveform V0(t), across the
capacitor is correctly depicted by :


17
Four point masses, each of mass m, are fixed at the corners of a square of side $$l$$. The square is
rotating with angular frequency $$\omega $$, about an axis passing through one of the corners of the square
and parallel to its diagonal, as shown in the figure. The angular momentum of the square about this
axis is :
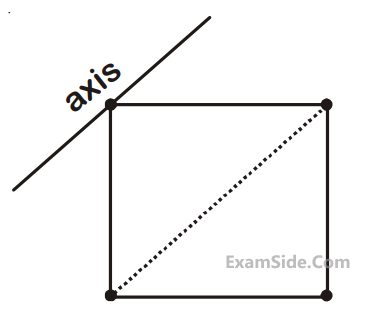

18
A screw gauge has 50 divisions on its circular scale. The circular scale is 4 units ahead of the
pitch scale marking, prior to use. Upon one complete rotation of the circular scale, a displacement of 0.5mm is noticed on the pitch scale. The nature of zero error involved and the least
count of the screw gauge, are respectively :
19
An electron, a doubly ionized helium ion (He++) and a proton are having the same kinetic energy.
The relation between their respective de-Broglie wavelengths $$\lambda $$e, $$\lambda $$He++ and $$\lambda $$p is :
20
A part of a complete circuit is shown in the figure. At some instant, the value of current I is 1A and
it is decreasing at a rate
of 102 A s–1. The value of the potential difference VP – VQ , (in volts) at that instant, is _________.

of 102 A s–1. The value of the potential difference VP – VQ , (in volts) at that instant, is _________.

21
Initially a gas of diatomic molecules is contained in a cylinder of volume V1
at a pressure P1
and
temperature 250 K. Assuming that 25% of the molecules get dissociated causing a change in
number of moles. The pressure of the resulting gas at temperature 2000 K, when contained in a
volume 2V1
is given by P2
. The ratio $${{{P_2}} \over {{P_1}}}$$
is ________.
22
The density of a solid metal sphere is determined by measuring its mass and its diameter. The
maximum error in the density of the sphere is $$\left( {{x \over {100}}} \right)$$ %. If the relative errors in measuring the mass
and the diameter are 6.0% and 1.5% respectively, the value of x is_______.
23
Suppose that intensity of a laser is $${{315} \over \pi }$$ W/m2.
The rms electric field, in units of V/m associated with this source is close to the nearest integer is __________.
$$ \in $$0 = 8.86 × 10–12 C2 Nm–2; c = 3 × 108 ms–1)
The rms electric field, in units of V/m associated with this source is close to the nearest integer is __________.
$$ \in $$0 = 8.86 × 10–12 C2 Nm–2; c = 3 × 108 ms–1)