JEE Main 2021 (Online) 22th July Evening Shift
Paper was held on
Thu, Jul 22, 2021 9:30 AM
Chemistry
1
Which one of the following statements for D.I. Mendeleeff, is incorrect?
2
Which purification technique is used for high boiling organic liquid compound (decomposes near its boiling point)?
3
Which of the following compounds will provide a tertiary alcohol or reaction with excess of CH3MgBr followed by hydrolysis?
4
Which of the following compounds does not exhibit resonance?
5

In the chemical reactions given above A and B respectively are :
6
Isotope(s) of hydrogen which emits low energy $$\beta$$$$-$$ particles with t1/2 value > 12 years is/are
7
Match List-I with List-II :
Choose the correct answer from the options given below :
| List-I (Species) |
List-II (Hybrid Orbitals) |
||
|---|---|---|---|
| (a) | $$S{F_4}$$ | (i) | $$s{p^3}{d^2}$$ |
| (b) | $$I{F_5}$$ | (ii) | $${d^2}s{p^3}$$ |
| (c) | $$NO_2^ + $$ | (iii) | $$s{p^3}d$$ |
| (d) | $$NH_4^ + $$ | (iv) | $$s{p^3}$$ |
| (v) | $$sp$$ |
Choose the correct answer from the options given below :
8
Which of the following molecules does not show stereo isomerism?
9
Which one of the following group-15 hydride is the strongest reducing agent?
10
The set having ions which are coloured and paramagnetic both is :
11
Thiamine and pyridoxine are also known respectively as :
12
An organic compound A (C6H6O) gives dark green colouration with ferric chloride. On treatment with CHCl3 and KOH, followed by acidification gives compound B. Compound B can also be obtained from compound C on reaction with pyridinium chlorochromate (PCC). Identify A, B and C.
13
Which one of the following reactions does not occur?
14
Which one of the following 0.06 M aqueous solutions has lowest freezing point?
15
The total number of unpaired electrons present in [Co(NH3)6]Cl2 and [Co(NH3)6]Cl3 is :
16
Methylation of 10 g of benzene gave 9.2 g of toluene. Calculate the percentage yield of toluene __________. (Nearest integer)
17
The number of acyclic structural isomers (including geometrical isomers) for pentene are ___________
18
Assume a cell with the following reaction
$$C{u_{(s)}} + 2A{g^ + }(1 \times {10^{ - 3}}M) \to C{u^{2 + }}(0.250M) + 2A{g_{(s)}}$$
$$E_{cell}^\Theta = 2.97$$ V
Ecell for the above reaction is ______________ V. (Nearest integer)
[Given : log 2.5 = 0.3979, T = 298 K]
$$C{u_{(s)}} + 2A{g^ + }(1 \times {10^{ - 3}}M) \to C{u^{2 + }}(0.250M) + 2A{g_{(s)}}$$
$$E_{cell}^\Theta = 2.97$$ V
Ecell for the above reaction is ______________ V. (Nearest integer)
[Given : log 2.5 = 0.3979, T = 298 K]
19
Value of KP for the equilibrium reaction
N2O4(g) $$\rightleftharpoons$$ 2NO2(g) at 288 K is 47.9. The KC for this reaction at same temperature is ____________. (Nearest integer)
(R = 0.083 L bar K$$-$$1 mol$$-$$1)
N2O4(g) $$\rightleftharpoons$$ 2NO2(g) at 288 K is 47.9. The KC for this reaction at same temperature is ____________. (Nearest integer)
(R = 0.083 L bar K$$-$$1 mol$$-$$1)
20
If the standard molar enthalpy change for combustion of graphite powder is $$-$$2.48 $$\times$$ 102 kJ mol$$-$$1, the amount of heat generated on combustion of 1 g of graphite powder is ___________ kJ. (Nearest integer)
21
Number of electrons that Vanadium (Z = 23) has in p-orbitals is equal to _____________
22
$${N_2}{O_{5(g)}} \to 2N{O_{2(g)}} + {1 \over 2}{O_{2(g)}}$$
In the above first order reaction the initial concentration of N2O5 is 2.40 $$\times$$ 10$$-$$2 mol L$$-$$1 at 318 K. The concentration of N2O5 after 1 hour was 1.60 $$\times$$ 10$$-$$2 mol L$$-$$1. The rate constant of the reaction at 318 K is ______________ $$\times$$ 10$$-$$3 min$$-$$1. (Nearest integer)
[Given : log 3 = 0.477, log 5 = 0.699]
In the above first order reaction the initial concentration of N2O5 is 2.40 $$\times$$ 10$$-$$2 mol L$$-$$1 at 318 K. The concentration of N2O5 after 1 hour was 1.60 $$\times$$ 10$$-$$2 mol L$$-$$1. The rate constant of the reaction at 318 K is ______________ $$\times$$ 10$$-$$3 min$$-$$1. (Nearest integer)
[Given : log 3 = 0.477, log 5 = 0.699]
23
If the concentration of glucose (C6H12O6) in blood is 0.72 g L$$-$$1, the molarity of glucose in blood is ____________ $$\times$$ 10$$-$$3 M. (Nearest integer)
[Given : Atomic mass of C = 12, H = 1, O = 16 u]
[Given : Atomic mass of C = 12, H = 1, O = 16 u]
Mathematics
1
Let Sn denote the sum of first n-terms of an arithmetic progression. If S10 = 530, S5 = 140, then S20 $$-$$ S6 is equal to:
2
Let f : R $$\to$$ R be defined as
$$f(x) = \left\{ {\matrix{ { - {4 \over 3}{x^3} + 2{x^2} + 3x,} & {x > 0} \cr {3x{e^x},} & {x \le 0} \cr } } \right.$$. Then f is increasing function in the interval
$$f(x) = \left\{ {\matrix{ { - {4 \over 3}{x^3} + 2{x^2} + 3x,} & {x > 0} \cr {3x{e^x},} & {x \le 0} \cr } } \right.$$. Then f is increasing function in the interval
3
Let y = y(x) be the solution of the differential equation $$\cos e{c^2}xdy + 2dx = (1 + y\cos 2x)\cos e{c^2}xdx$$, with $$y\left( {{\pi \over 4}} \right) = 0$$. Then, the value of $${(y(0) + 1)^2}$$ is equal to :
4
Four dice are thrown simultaneously and the numbers shown on these dice are recorded in 2 $$\times$$ 2 matrices. The probability that such formed matrix have all different entries and are non-singular, is :
5
If $$\int\limits_0^{100\pi } {{{{{\sin }^2}x} \over {{e^{\left( {{x \over \pi } - \left[ {{x \over \pi }} \right]} \right)}}}}dx = {{\alpha {\pi ^3}} \over {1 + 4{\pi ^2}}},\alpha \in R} $$ where [x] is the greatest integer less than or equal to x, then the value of $$\alpha$$ is :
6
The values of $$\lambda$$ and $$\mu$$ such that the system of equations $$x + y + z = 6$$, $$3x + 5y + 5z = 26$$, $$x + 2y + \lambda z = \mu $$ has no solution, are :
7
If the shortest distance between the straight lines $$3(x - 1) = 6(y - 2) = 2(z - 1)$$ and $$4(x - 2) = 2(y - \lambda ) = (z - 3),\lambda \in R$$ is $${1 \over {\sqrt {38} }}$$, then the integral value of $$\lambda$$ is equal to :
8
Let A = [aij] be a real matrix of order 3 $$\times$$ 3, such that ai1 + ai2 + ai3 = 1, for i = 1, 2, 3. Then, the sum of all the entries of the matrix A3 is equal to :
9
Let [x] denote the greatest integer less than or equal to x. Then, the values of x$$\in$$R satisfying the equation $${[{e^x}]^2} + [{e^x} + 1] - 3 = 0$$ lie in the interval :
10
Let the circle S : 36x2 + 36y2 $$-$$ 108x + 120y + C = 0 be such that it neither intersects nor touches the co-ordinate axes. If the point of intersection of the lines, x $$-$$ 2y = 4 and 2x $$-$$ y = 5 lies inside the circle S, then :
11
Let n denote the number of solutions of the equation z2 + 3$$\overline z $$ = 0, where z is a complex number. Then the value of $$\sum\limits_{k = 0}^\infty {{1 \over {{n^k}}}} $$ is equal to :
12
If the domain of the function $$f(x) = {{{{\cos }^{ - 1}}\sqrt {{x^2} - x + 1} } \over {\sqrt {{{\sin }^{ - 1}}\left( {{{2x - 1} \over 2}} \right)} }}$$ is the interval ($$\alpha$$, $$\beta$$], then $$\alpha$$ + $$\beta$$ is equal to :
13
Let f : R $$\to$$ R be defined as $$f(x) = \left\{ {\matrix{
{{{{x^3}} \over {{{(1 - \cos 2x)}^2}}}{{\log }_e}\left( {{{1 + 2x{e^{ - 2x}}} \over {{{(1 - x{e^{ - x}})}^2}}}} \right),} & {x \ne 0} \cr
{\alpha ,} & {x = 0} \cr
} } \right.$$
If f is continuous at x = 0, then $$\alpha$$ is equal to :
If f is continuous at x = 0, then $$\alpha$$ is equal to :
14
Let $${E_1}:{{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1,a > b$$. Let E2 be another ellipse such that it touches the end points of major axis of E1 and the foci of E2 are the end points of minor axis of E1. If E1 and E2 have same eccentricities, then its value is :
15
Let A = {0, 1, 2, 3, 4, 5, 6, 7}. Then the number of bijective functions f : A $$\to$$ A such that f(1) + f(2) = 3 $$-$$ f(3) is equal to
16
If the digits are not allowed to repeat in any number formed by using the digits 0, 2, 4, 6, 8, then the number of all numbers greater than 10,000 is equal to _____________.
17
Let $$A = \left[ {\matrix{
0 & 1 & 0 \cr
1 & 0 & 0 \cr
0 & 0 & 1 \cr
} } \right]$$. Then the number of 3 $$\times$$ 3 matrices B with entries from the set {1, 2, 3, 4, 5} and satisfying AB = BA is ____________.
18
Consider the following frequency distribution :
If mean = $${{309} \over {22}}$$ and median = 14, then the value (a $$-$$ b)2 is equal to _____________.
| Class : | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 |
|---|---|---|---|---|---|
| Frequency : | $$a $$ | $$b$$ | 12 | 9 | 5 |
If mean = $${{309} \over {22}}$$ and median = 14, then the value (a $$-$$ b)2 is equal to _____________.
19
The sum of all the elements in the set {n$$\in$$ {1, 2, ....., 100} | H.C.F. of n and 2040 is 1} is equal to _____________.
20
The area (in sq. units) of the region bounded by the curves x2 + 2y $$-$$ 1 = 0, y2 + 4x $$-$$ 4 = 0 and y2 $$-$$ 4x $$-$$ 4 = 0, in the upper half plane is _______________.
21
Let f : R $$\to$$ R be a function defined as $$f(x) = \left\{ {\matrix{
{3\left( {1 - {{|x|} \over 2}} \right)} & {if} & {|x|\, \le 2} \cr
0 & {if} & {|x|\, > 2} \cr
} } \right.$$
Let g : R $$\to$$ R be given by $$g(x) = f(x + 2) - f(x - 2)$$. If n and m denote the number of points in R where g is not continuous and not differentiable, respectively, then n + m is equal to ______________.
Let g : R $$\to$$ R be given by $$g(x) = f(x + 2) - f(x - 2)$$. If n and m denote the number of points in R where g is not continuous and not differentiable, respectively, then n + m is equal to ______________.
22
If the constant term, in binomial expansion of $${\left( {2{x^r} + {1 \over {{x^2}}}} \right)^{10}}$$ is 180, then r is equal to __________________.
23
Let y = y(x) be the solution of the differential equation $$\left( {(x + 2){e^{\left( {{{y + 1} \over {x + 2}}} \right)}} + (y + 1)} \right)dx = (x + 2)dy$$, y(1) = 1. If the domain of y = y(x) is an open interval ($$\alpha$$, $$\beta$$), then | $$\alpha$$ + $$\beta$$| is equal to ______________.
Physics
1
What will be the projection of vector $$\overrightarrow A = \widehat i + \widehat j + \widehat k$$ on vector $$\overrightarrow B = \widehat i + \widehat j$$ ?
2
A Copper (Cu) rod of length 25 cm and cross-sectional area 3 mm2 is joined with a similar Aluminium (Al) rod as shown in figure. Find the resistance of the combination between the ends A and B.
(Take Resistivity of Copper = 1.7 $$\times$$ 10$$-$$8 $$\Omega$$m and Resistivity of Aluminium = 2.6 $$\times$$ 10$$-$$8 $$\Omega$$m)

(Take Resistivity of Copper = 1.7 $$\times$$ 10$$-$$8 $$\Omega$$m and Resistivity of Aluminium = 2.6 $$\times$$ 10$$-$$8 $$\Omega$$m)

3
In a circuit consisting of a capacitance and a generator with alternating emf Eg = Eg0 sin$$\omega$$t, VC and IC are the voltage and current. Correct phasor diagram for such circuit is
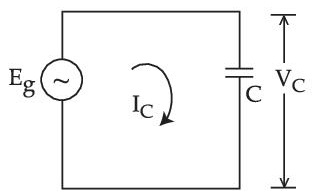

4
A porter lifts a heavy suitcase of mass 80 kg and at the destination lowers it down by a distance of 80 cm with a constant velocity. Calculate the work done by the porter in lowering the suitcase.
(take g = 9.8 ms$$-$$2)
(take g = 9.8 ms$$-$$2)
5
Consider a situation in which a ring, a solid cylinder and a solid sphere roll down on the same inclined plane without slipping. Assume that they start rolling from rest and having identical diameter.
The correct statement for this situation is
The correct statement for this situation is
6
Intensity of sunlight is observed as 0.092 Wm$$-$$2 at a point in free space. What will be the peak value of magnetic field at the point?
($${\varepsilon _0} = 8.85 \times {10^{ - 12}}{C^2}{N^{ - 1}}{m^{ - 2}}$$)
($${\varepsilon _0} = 8.85 \times {10^{ - 12}}{C^2}{N^{ - 1}}{m^{ - 2}}$$)
7
A body is projected vertically upwards from the surface of earth with a velocity sufficient enough to carry it to infinity. The time taken by it to reach height h is ___________ s.
8
An electric dipole is placed on x-axis in proximity to a line charge of linear charge density 3.0 $$\times$$ 10$$-$$6 C/m. Line charge is placed on z-axis and positive and negative charge of dipole is at a distance of 10 mm and 12 mm from the origin respectively. If total force of 4N is exerted on the dipole, find out the amount of positive or negative charge of the dipole.
9
A nucleus with mass number 184 initially at rest emits an $$\alpha$$-particle. If the Q value of the reaction is 5.5 MeV, calculate the kinetic energy of the $$\alpha$$-particle.
10
A bullet of '4 g' mass is fired from a gun of mass 4 kg. If the bullet moves with the muzzle speed of 50 ms$$-$$1, the impulse imparted to the gun and velocity of recoil of gun are :
11
Statement I : The ferromagnetic property depends on temperature. At high temperature, ferromagnet becomes paramagnet.
Statement II : At high temperature, the domain wall area of a ferromagnetic substance increases.
In the light of the above statements, choose the most appropriate answer from the options given below :
Statement II : At high temperature, the domain wall area of a ferromagnetic substance increases.
In the light of the above statements, choose the most appropriate answer from the options given below :
12
Match List - I with List - II
Choose the correct answer from the options given below
| List - I | List - II | ||
|---|---|---|---|
| (a) | $$\omega L > {1 \over {\omega C}}$$ | (i) | Current is in phase with emf |
| (b) | $$\omega L = {1 \over {\omega C}}$$ | (ii) | Current lags behind the applied emf |
| (c) | $$\omega L < {1 \over {\omega C}}$$ | (iii) | Maximum current occurs |
| (d) | Resonant frequency | (iv) | Current leads the emf |
Choose the correct answer from the options given below
13
A ray of light passes from a denser medium to a rarer medium at an angle of incidence i. The reflected and refracted rays make an angle of 90$$^\circ$$ with each other. The angle of reflection and refraction are respectively r and r'. The critical angle is given by


14
An electron of mass me and a proton of mass mp are accelerated through the same potential difference. The ratio of the de-Broglie wavelength associated with the electron to that with the proton is
15
What will be the average value of energy for a monoatomic gas in thermal equilibrium at temperature T?
16
T0 is the time period of a simple pendulum at a place. if the length of the pendulum is reduced to $${1 \over {16}}$$ times of its initial value, the modified time period is :
17
The motion of a mass on a spring, with spring constant K is as shown in figure.
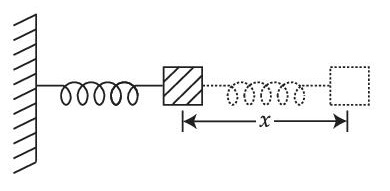
The equation of motion is given by
x(t) = A sin$$\omega$$t + B cos$$\omega$$t with $$\omega$$ = $$\sqrt {{K \over m}} $$
Suppose that at time t = 0, the position of mass is x(0) and velocity v(0), then its displacement can also be represented as x(t) = C cos($$\omega$$t $$-$$ $$\phi$$), where C and $$\phi$$ are :

The equation of motion is given by
x(t) = A sin$$\omega$$t + B cos$$\omega$$t with $$\omega$$ = $$\sqrt {{K \over m}} $$
Suppose that at time t = 0, the position of mass is x(0) and velocity v(0), then its displacement can also be represented as x(t) = C cos($$\omega$$t $$-$$ $$\phi$$), where C and $$\phi$$ are :
18
Consider a situation in which reserve biased current of a particular P-N junction increases when it is exposed to a light of wavelength $$\le$$ 621 nm. During this process, enhancement in carrier concentration takes place due to generation of hole-electron pairs. The value of band gap is nearly.
19
A ray of light passing through a prism ($$\mu$$ = $$\sqrt 3 $$) suffers minimum deviation. It is found that the angle of incidence is double the angle of refraction within the prism. Then, the angle of prism is _____________ (in degrees).
20
Three students S1, S2 and S3 perform an experiment for determining the acceleration due to gravity (g) using a simple pendulum. They use different lengths of pendulum and record time for different number of oscillations. The observations are as shown in the table.
(Least count of length = 0.1 cm and Least count for time = 0.1 s)
If E1, E2 and E3 are the percentage errors in 'g' for students 1, 2 and 3 respectively, then the minimum percentage error is obtained by student no. ______________.
| Student No. |
Length of Pendulum (cm) |
No. of oscillations (n) |
Total time for n oscillations |
Time period (s) |
|---|---|---|---|---|
| 1 | 64.0 | 8 | 128.0 | 16.0 |
| 2 | 64.0 | 4 | 64.0 | 16.0 |
| 3 | 20.0 | 4 | 36.0 | 9.0 |
(Least count of length = 0.1 cm and Least count for time = 0.1 s)
If E1, E2 and E3 are the percentage errors in 'g' for students 1, 2 and 3 respectively, then the minimum percentage error is obtained by student no. ______________.
21
Three particles P, Q and R are moving along the vectors $$\overrightarrow A = \widehat i + \widehat j$$, $$\overrightarrow B = \widehat j + \widehat k$$ and $$\overrightarrow C = - \widehat i + \widehat j$$ respectively. They strike on a point and start to move in different directions. Now particle P is moving normal to the plane which contains vector $$\overrightarrow A $$ and $$\overrightarrow B $$. Similarly particle Q is moving normal to the plane which contains vector $$\overrightarrow A $$ and $$\overrightarrow C $$. The angle between the direction of motion of P and Q is $${\cos ^{ - 1}}\left( {{1 \over {\sqrt x }}} \right)$$. Then the value of x is _______________.
22
In a given circuit diagram, a 5 V zener diode along with a series resistance is connected across a 50 V power supply. The minimum value of the resistance required, if the maximum zener current is 90 mA will be __________ $$\Omega$$.


23
The total charge enclosed in an incremental volume of 2 $$\times$$ 10$$-$$9 m3 located at the origin is ___________ nC, if electric flux density of its field is found as
D = e$$-$$x sin y $$\widehat i$$ $$-$$ e$$-$$x cos y $$\widehat j$$ + 2z $$\widehat k$$ C/m2
D = e$$-$$x sin y $$\widehat i$$ $$-$$ e$$-$$x cos y $$\widehat j$$ + 2z $$\widehat k$$ C/m2
24
The position of the centre of mass of a uniform semi-circular wire of radius 'R' placed in x-y plane with its centre at the origin and the line joining its ends as x-axis is given by $$\left( {0,{{xR} \over \pi }} \right)$$. Then, the value of | x | is ______________.
25
In an electric circuit, a cell of certain emf provides a potential difference of 1.25 V across a load resistance of 5$$\Omega$$. However, it provides a potential difference of 1 V across a load resistance of 2$$\Omega$$. The emf of the cell is given by $${x \over {10}}V$$. Then the value of x is ______________.
26
The area of cross-section of a railway track is 0.01 m2. The temperature variation is 10$$^\circ$$C. Coefficient of liner expansion of material of track is 10$$-$$5/$$^\circ$$C. The energy stored per meter in the track is ____________ J/m.
(Young's modulus of material of track is 1011 Nm$$-$$2)
(Young's modulus of material of track is 1011 Nm$$-$$2)
27
The centre of a wheel rolling on a plane surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre will be moving at a speed $$\sqrt x {v_0}$$. Then the value of x is _____________.