JEE Main 2019 (Online) 11th January Morning Slot
Paper was held on
Fri, Jan 11, 2019 3:30 AM
Chemistry
1
For the chemical reaction X $$\rightleftharpoons$$ Y, the standard reaction Gibbs energy depends on temperature T (in K) as
$$\Delta $$rGo (in kJ mol–1) = 120 $$ - {3 \over 8}$$ T.
The major component of the reaction mixture at T is :
The major component of the reaction mixture at T is :
2
Consider the reaction
N2(g) + 3H2(g) $$\rightleftharpoons$$ 2NH3(g)
The equilibrium constant of the above reaction is Kp. If pure ammonia is left to dissociate, the partial pressure of ammonia at equilibrium is given by (Assume that PNH3 << Ptotal at equilibrium)
N2(g) + 3H2(g) $$\rightleftharpoons$$ 2NH3(g)
The equilibrium constant of the above reaction is Kp. If pure ammonia is left to dissociate, the partial pressure of ammonia at equilibrium is given by (Assume that PNH3 << Ptotal at equilibrium)
3
A 10 mg effervescent tablet containing sodium bicarbonate and oxalic acid releases 0.25 ml of CO2 at T = 298.15 K and p = 1 bar. If molar volume of CO2 is 25.0 L under such condition, what is the percentage of sodium bicarbonate in each tablet ?
[Molar mass of NaHCO3 = 84 g mol–1]
[Molar mass of NaHCO3 = 84 g mol–1]
4
The correct order of the atomic radii of C, Cs, Al, and S is :
5
For the cell Zn(s) |Zn2+ (aq)| |Mx+ (aq)| M(s), different half cells and their standard electrode potentials are given below :
If $$E_{z{n^{2 + }}/zn}^0$$ = $$-$$ 0.76 V, which cathode will give maximum value of Eocell per electron transferred?
| Mx+ (aq)/M(s) | Au3+(aq)/Au(s) | Ag+(aq)/Ag(s) | Fe3+(aq)/Fe2+ (aq) | Fe2+(aq)/Fe(s) |
|---|---|---|---|---|
| E0Mx+/M/(V) | 1.40 | 0.80 | 0.77 | $$-$$0.44 |
If $$E_{z{n^{2 + }}/zn}^0$$ = $$-$$ 0.76 V, which cathode will give maximum value of Eocell per electron transferred?
6
The element that usually does NOT show variable oxidation states is :
7
Heat treatment of muscular pain involves radiation of wavelength of about 900 nm. Which spectral line of H atom is suitable for this purpose?
[RH = 1 $$ \times $$ 105 cm–1, h = 6.6 $$ \times $$ 10–34 Js, c = 3 $$ \times $$ 108 ms–1]
[RH = 1 $$ \times $$ 105 cm–1, h = 6.6 $$ \times $$ 10–34 Js, c = 3 $$ \times $$ 108 ms–1]
8
Match the metals (column I) with the coordination compound(s)/enzyme(s) (column II)
| (Column I) Metals |
(Column II) Coordination compounds(s) enzyme(s) |
||
|---|---|---|---|
| (A) | Co | (i) | Wilkinson catalyst |
| (B) | Zn | (ii) | Chlorophyl |
| (C) | Rh | (iii) | Vitamin B12 |
| (D) | Mg | (iv) | Carbonic anhydrase |
9
If a reaction follows the Arrhenius equation, the plot ln k vs $${1 \over {\left( {RT} \right)}}$$ gives straight line with a gradient ($$-$$ y) unit.
The energy required to active the reactant is :
The energy required to active the reactant is :
10
The major product of the following reaction is :


11
The major product of the following reaction is :


12
The major product of the following reaction is


13
Which compound (s) out of the following is/are not aromatic ?


14
Among the following compounds, which one is found in RNA ?
15
The major product of the following reaction is :


16
Two blocks of the same metal having same mass and at temperature T1 and T2, respectively, are brought in contact with each other and allowed to attain thermal equilibrium at constant pressure. The change in entropy, $$\Delta $$S, for this process is :
17
The freezing point of a diluted milk sample is found to be –0.2oC, while it should have been –0.5oC for pure milk. How much water has been added to pure milk to make the diluted sample?
18
The correct match between items I and II is :
| Item-I (Mixture) | Item-II (Seperation method) | ||
|---|---|---|---|
| (A) | H2O : Sugar | (P) | Sublimation |
| (B) | H2O : Aniline | (Q) | Recrystallization |
| (C) | H2O : Toluene |
(R) | Steam distillation |
| (S) | Differential extraction | ||
19
An organic compound is estimated through Duma's method and was found to evolve 6 moles of CO2. 4 moles of H2O and 1 mole of nitrogen gas. The formula of the compound is :
Mathematics
1
The straight line x + 2y = 1 meets the coordinate axes at A and B. A circle is drawn through A, B and the origin. Then the sum of perpendicular distances from A and B on the tangent to the circle at the origin is :
2
If xloge(logex) $$-$$ x2 + y2 = 4(y > 0), then $${{dy} \over {dx}}$$ at x = e is equal to :
3
Let [x] denote the greatest integer less than or equal to x. Then $$\mathop {\lim }\limits_{x \to 0} {{\tan \left( {\pi {{\sin }^2}x} \right) + {{\left( {\left| x \right| - \sin \left( {x\left[ x \right]} \right)} \right)}^2}} \over {{x^2}}}$$
4
Let A = $$\left( {\matrix{
0 & {2q} & r \cr
p & q & { - r} \cr
p & { - q} & r \cr
} } \right).$$ If AAT = I3, then $$\left| p \right|$$ is :
5
If y(x) is the solution of the differential equation $${{dy} \over {dx}} + \left( {{{2x + 1} \over x}} \right)y = {e^{ - 2x}},\,\,x > 0,\,$$ where $$y\left( 1 \right) = {1 \over 2}{e^{ - 2}},$$ then
6
A square is inscribed in the circle x2 + y2
– 6x + 8y – 103 = 0 with its sides parallel to the coordinate axes.
Then the distance of the vertex of this square which is nearest to the origin is :
7
If one real root of the quadratic equation 81x2 + kx + 256 = 0 is cube of the other root, then a value of k is
8
The outcome of each of 30 items was observed; 10 items gave an outcome $${1 \over 2}$$ – d each, 10 items gave outcome $${1 \over 2}$$ each and the remaining 10 items gave outcome $${1 \over 2}$$+ d each. If the variance of this outcome data is $${4 \over 3}$$ then |d| equals :
9
The maximum value of the function f(x) = 3x3 – 18x2 + 27x – 40 on the set S = $$\left\{ {x\, \in R:{x^2} + 30 \le 11x} \right\}$$ is :
10
Let f : R $$ \to $$ R be defined by f(x) = $${x \over {1 + {x^2}}},x \in R$$. Then the range of f is :
11
Let $$\overrightarrow a = \widehat i + 2\widehat j + 4\widehat k,$$ $$\overrightarrow b = \widehat i + \lambda \widehat j + 4\widehat k$$ and $$\overrightarrow c = 2\widehat i + 4\widehat j + \left( {{\lambda ^2} - 1} \right)\widehat k$$ be coplanar vectors. Then the non-zero vector $$\overrightarrow a \times \overrightarrow c $$ is :
12
The sum of the real values of x for which the middle term in the binomial expansion of $${\left( {{{{x^3}} \over 3} + {3 \over x}} \right)^8}$$ equals 5670 is :
13
If $$\int {{{\sqrt {1 - {x^2}} } \over {{x^4}}}} $$ dx = A(x)$${\left( {\sqrt {1 - {x^2}} } \right)^m}$$ + C, for a suitable chosen integer m and a function A(x), where C is a constant of integration, then (A(x))m equals :
14
If the system of linear equations
2x + 2y + 3z = a
3x – y + 5z = b
x – 3y + 2z = c
where a, b, c are non zero real numbers, has more one solution, then :
2x + 2y + 3z = a
3x – y + 5z = b
x – 3y + 2z = c
where a, b, c are non zero real numbers, has more one solution, then :
15
The value of the integral $$\int\limits_{ - 2}^2 {{{{{\sin }^2}x} \over { \left[ {{x \over \pi }} \right] + {1 \over 2}}}} \,dx$$ (where [x] denotes the greatest integer less than or equal to x) is
16
The sum of an infinite geometric series with positive terms is 3 and the sum of the cubes of its terms is $${{27} \over {19}}$$.Then the common ratio of this series is :
17
Let $$f\left( x \right) = \left\{ {\matrix{
{ - 1} & { - 2 \le x < 0} \cr
{{x^2} - 1,} & {0 \le x \le 2} \cr
} } \right.$$ and
$$g(x) = \left| {f\left( x \right)} \right| + f\left( {\left| x \right|} \right).$$
Then, in the interval (–2, 2), g is :
$$g(x) = \left| {f\left( x \right)} \right| + f\left( {\left| x \right|} \right).$$
Then, in the interval (–2, 2), g is :
18
Two integers are selected at random from the set {1, 2, ...., 11}. Given that the sum of selected numbers is even, the conditional probability that both the numbers are even is :
19
Let $${\left( { - 2 - {1 \over 3}i} \right)^3} = {{x + iy} \over {27}}\left( {i = \sqrt { - 1} } \right),\,\,$$ where x and y are real numbers, then y $$-$$ x equals :
20
Let fk(x) = $${1 \over k}\left( {{{\sin }^k}x + {{\cos }^k}x} \right)$$ for k = 1, 2, 3, ... Then for all x $$ \in $$ R, the value of f4(x) $$-$$ f6(x) is equal to
21
Let a1, a2, . . . . . ., a10 be a G.P. If $${{{a_3}} \over {{a_1}}} = 25,$$ then $${{{a_9}} \over {{a_5}}}$$ equals
22
The area (in sq. units) of the region bounded by the curve x2 = 4y and the straight line x = 4y – 2 is :
Physics
1
An electromagnetic wave of intensity 50 Wm–2 enters in a medium of refractive index 'n' without any loss. The ratio of the magnitudes of electric, and the ratio of the magnitudes of magnetic fields of the wave before and after entering into the medium are respectively, given by:
2
Equation of travelling wave on a stretched string of linear density 5 g/m is y = 0.03 sin(450 t – 9x) where distance and time are measured in SI units. The tension in the string is :
3
A body is projected at t = 0 with a velocity 10 ms–1
at an angle of 60o with the horizontal. The radius of curvature of its trajectory at t = 1s is R. neglecting air resistance and taking acceleration due to gravity g = 10 ms–2, the value of R is :
4
A liquid of density $$\rho $$ is coming out of a hose pipe of radius a with horizontal speed $$\upsilon $$ and hits a mesh. 50% of
the liquid passes through the mesh unaffected. 25% looses all of its momentum and 25% comes back with the same speed. The resultant pressure on the mesh will be :
5
In a Wheatstone bridge(see fig.), Resistances P and Q are approximately equal. When R = 400 $$\Omega $$, the bridge
is balanced. On interchanging P and Q, the value of R, for balance, is 405 $$\Omega $$. The value of X is close to :


6
In the given circuit the current through Zener Diode is close to:


7
An equilateral triangle ABC is cut from a thin solid sheet of wood. (see figure) D, E and F are the mid-points of its sides as shown and G is the centre of the triangle. The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane of the triangle is I0. If the smaller triangle DEF is removed from ABC, the moment of inertia of the remaining figure about the same axis is I. then :
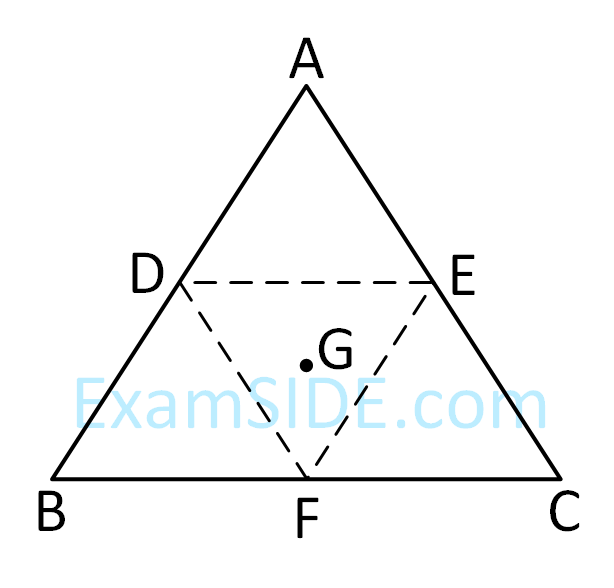

8
A slab is subjected to two forces $$\overrightarrow {{F_1}} $$ and $$\overrightarrow {{F_2}} $$ of same magnitude F as shown in the figure. Force $$\overrightarrow {{F_2}} $$ is in XY-plane while force $$\overrightarrow {{F_1}} $$ acts along z = axis at the point $$\left( {2\overrightarrow i + 3\overrightarrow j } \right).$$. The moment of these forces about point O will be :
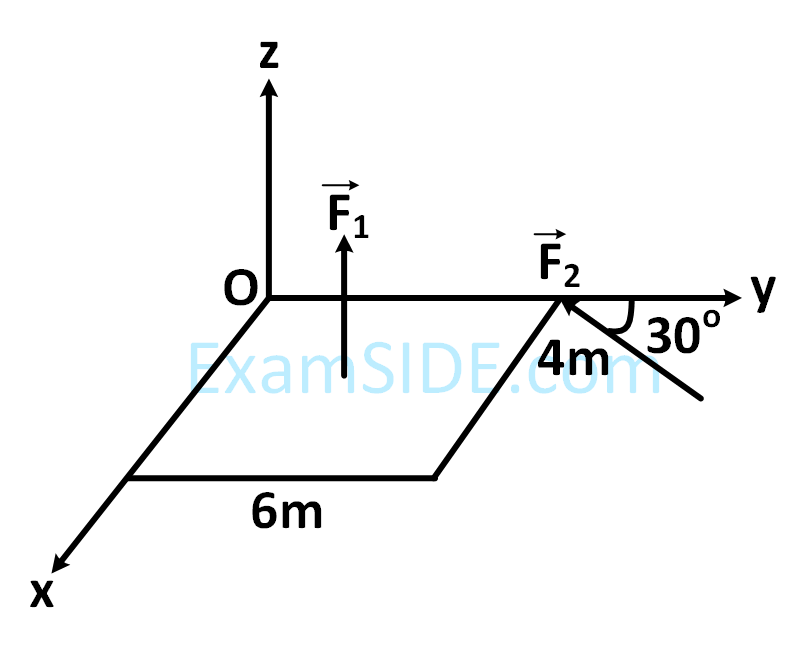

9
A body of mass 1 kg falls freely from a height of 100 m, on a platform mass 3 kg which is mounted on a spring having spring constant k = 1.25 $$ \times $$ 106 N/m. The body sticks to the platform and the spring's maximum compression is found to be x. Given that g = 10 ms–2
, the value of x will be close to :
10
In the circuit shown,
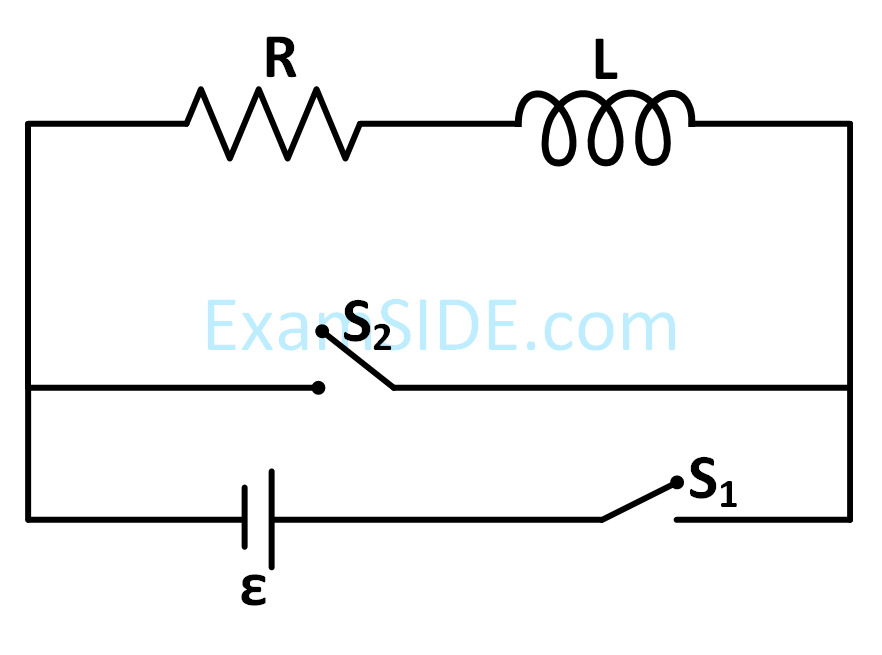
the switch S1 is closed at time t = 0 and the switch S2 is kept open. At some later time(t0), the switch S1 is opened and S2 is closed. The behavior of the current I as a function of time 't' is given by :

the switch S1 is closed at time t = 0 and the switch S2 is kept open. At some later time(t0), the switch S1 is opened and S2 is closed. The behavior of the current I as a function of time 't' is given by :
11
The resistance of the meter bridge AB in given figure is 4 $$\Omega $$. With a cell of emf $$\varepsilon $$ = 0.5 V and rheostat
resistance Rh = 2 $$\Omega $$ the null point is obtained at some point J. When the cell is replaced by another one of emf $$\varepsilon $$ = $$\varepsilon $$2 the same null point J is found for Rh = 6 $$\Omega $$. The emf $$\varepsilon $$2 is, :


12
The given graph shows variation (with distance r form centre) of :


13
Three charges Q, + q and + q are placed at the vertices of a right-angle isosceles triangle as shown below. The net electrostatic energy of the configuration is zero, if the value of Q is :


14
In the figure shown below, the charge on the left plate of the 10$$\mu $$F capacitor is –30$$\mu $$C. The charge on the right plate of the 6 $$\mu $$F capacitor is :


15
The variation of refractive index of a crown glass thin prism with wavelength of the incident light is shown. Which of the following graphs is the correct one, if Dm is the angle of minimum deviation?


16
In a Young's double slit experiment, the path difference, at a certain point on the screen, between two interfering waves is $${1 \over 8}$$ th of wavelength. The ratio of the intensity at this point to that at the centre of a bright fringe is close to :
17
Two equal resistances when connected in series to a battery, consume electric power of 60 W. If these resistances are now connected in parallel combination to the same battery, the electric power consumed will be :
18
The force of interaction between two atoms is given by F = $$\alpha $$$$\beta $$exp $$\left( { - {{{x^2}} \over {\alpha kt}}} \right)$$; where x is the distance, k is the Boltzmann constant and T is temperature and $$\alpha $$ and $$\beta $$ are two constants. The dimension of $$\beta $$ is :
19
There are two long co-axial solenoids of same length $$l$$. The inner and outer coils have radii r1 and r2 and number of turns per unit length n1 and n2, respectively. The ratio of mutual inductance to the self - inductance of the inner-coil is :
20
A particle is moving along a circular path with a constant speed of 10 ms–1. What is the magnitude of the change in velocity of the particle, when it moves through an angle of 60o around the centre of the circle?
21
If the de Broglie wavelength of an electron is equal to the 10–3 times the wavelength of a photon of frequency 6 $$ \times $$ 1014 Hz, then the speed of electron is equal to : (Speed of light = 3 $$ \times $$ 108 m/s, Planck's constant = 6.63 $$ \times $$
10–34 J.s, Mass of electron = 9.1 $$ \times $$ 10–31 kg)
22
An object is at a distance of 20 m from a convex lens of focal length 0.3 m. The lens forms an image of the object. If the object moves away from the lens at a speed of 5 m/s, the speed and direction of the image will be :
23
In an experiment, electrons are accelerated, from rest, by applying a voltage of 500 V. Calculate the radius of the path if a magnetic field 100 mT is then applied. [Charge of the electron = 1.6 $$ \times $$ 10–19 C Mass of the electron = 9.1 $$ \times $$ 10–31 kg]
24
A hydrogen atom, initially in the ground state is excited by absorbing a photon of wavelength 980$$\mathop A\limits^ \circ $$. The radius of the atom in the excited state, in terms of Bohr radius a0 will be : (hc = 12500 eV$$\mathop A\limits^ \circ $$)
25
A satellite is revolving in a circular orbit at a height h form the earth surface, such that h < < R where R is the earth. Assuming that the effect of earth's atmosphere can be neglected the minimum increase in the speed required so that the satellite could escape from the gravitational field of earth is :
26
Ice at –20oC is added to 50 g of water at 40oC. When the temperature of the mixture reaches 0oC, it is found that 20 g of ice is still unmelted. The amount of ice added to the water was close to (Specific heat of water = 4.2J/g/oC Specific heat of Ice = 2.1J/g/oC Heat of fusion of water at 0oC= 334J/g)
27
A rigid diatomic ideal gas undergoes an adiabatic process at room temperature. The relation between temperature and volume for this process is TVx = constant, then x is :
28
A gas mixture consists of 3 moles of oxygen and 5 moles of argon at temperature T. considering only translational and rotational modes, the total internal energy of the system is :
29
A particle undergoing simple harmonic motion has time dependent displacement given by x(t) = Asin$${{\pi t} \over {90}}$$. The ratio of kinetic to potential energy of this particle at t = 210 s will be: