JEE Main 2021 (Online) 18th March Morning Shift
Paper was held on
Thu, Mar 18, 2021 3:30 AM
Chemistry
1

Considering the above reaction, X and Y respectively are :
2
The ionic radius of Na+ ions is 1.02 $$\mathop A\limits^o $$. The ionic radii (in $$\mathop A\limits^o $$) of Mg2+ and Al3+, respectively, are
3
Reaction of Grignard reagent, C2H5MgBr with C8H8O followed by hydrolysis gives compound "A" which reacts instantly with Lucas reagent to give compound B, C10H13Cl. The Compound B is :
4
Reagent, 1-napthylamine and sulphanilic acid in acetic acid is used for the detection of
5
A non-reducing sugar "A" hydrolyses to give two reducing mono saccharides. Sugar A is
6

Consider the above chemical reaction and identify product "A"
7
Match List - I with List - II
Choose the most appropriate answer from the options given below :
| List - I |
List - II |
||
|---|---|---|---|
| (a) | Chlorophyll | (i) | Ruthenium |
| (b) | Vitamin-$${B_{12}}$$ | (ii) | Platinum |
| (c) | Anticancer drug | (iii) | Cobalt |
| (d) | Grubbs catalyst | (iv) | Magnesium |
Choose the most appropriate answer from the options given below :
8
Match List - I with List - II :
List - I (Chemicals)
(a) Alcoholic potassium hydroxide
(b) Pd/BaSO4
(c) BHC (Benzene hexachloride)
(d) Polyacetylene
List - II (Use / Preparation / Constituent)
(i) Electrodes in batteries
(ii) Obtained by addition reaction
(iii) Used for $$\beta$$ - elimination reaction
(iv) Lindlar's catalyst
Choose the most appropriate match :
List - I (Chemicals)
(a) Alcoholic potassium hydroxide
(b) Pd/BaSO4
(c) BHC (Benzene hexachloride)
(d) Polyacetylene
List - II (Use / Preparation / Constituent)
(i) Electrodes in batteries
(ii) Obtained by addition reaction
(iii) Used for $$\beta$$ - elimination reaction
(iv) Lindlar's catalyst
Choose the most appropriate match :
9
Compound with molecular formula C3H6O can show :
10
The correct structures of trans-[NiBr2(PPh3)2] and meridonial-[Co(NH3)3(NO2)3], respectively, are
11
A certain orbital has no angular nodes and two radial nodes. The orbital is :
12

Considering the above chemical reaction, identify the product "X" :
13
Match List - I with List - II
Choose the most appropriate answer from the options given below :
| List - I (process) |
List - II (catalyst) |
||
|---|---|---|---|
| (a) | Deacron's process | (i) | ZSM-5 |
| (b) | Contact process | (ii) | $$CuC{l_2}$$ |
| (c) | Cracking of hydrocarbons | (iii) | Particles 'Ni' |
| (d) | Hydrogenation of vegetable oils | (iv) | $${V_2}{O_5}$$ |
Choose the most appropriate answer from the options given below :
14
Given below are two statements : One is labelled as Assertion A and the other labelled as reason R
Assertion A : During the boiling of water having temporary hardness, Mg(HCO3)2 is converted to MgCO3.
Reason R : The solubility product of Mg(OH)2 is greater than that of MgCO3.
In the light of the above statements, choose the most appropriate answer from the options given below :
Assertion A : During the boiling of water having temporary hardness, Mg(HCO3)2 is converted to MgCO3.
Reason R : The solubility product of Mg(OH)2 is greater than that of MgCO3.
In the light of the above statements, choose the most appropriate answer from the options given below :
15
AX is a covalent diatomic molecule where A and X are second row elements of periodic table. Based on Molecular orbital theory, the bond order of AX is 2.5. The total number of electrons in AX is __________. (Round off to the Nearest Integer).
16
In order to prepare a buffer solution of pH 5.74, sodium acetate is added to acetic acid. If the concentration of acetic acid in the buffer is 1.0 M, the concentration of sodium acetate in the buffer is ___________ M. (Round off to the Nearest Integer). [Given : pKa (acetic acid) = 4.74]
17
2NO(g) + Cl2(g) $$\rightleftharpoons $$ 2NOCl(s)
This reaction was studied at $$-$$10$$^\circ$$ and the following data was obtained
$${[NO]_0}$$ and $${[C{l_2}]_0}$$ are the initial concentrations and r0 is the initial reaction rate.
The overall order of the reaction is __________. (Round off to the Nearest Integer).
This reaction was studied at $$-$$10$$^\circ$$ and the following data was obtained
| Run | $${[NO]_0}$$ | $${[C{l_2}]_0}$$ | $${r_0}$$ |
|---|---|---|---|
| 1 | 0.10 | 0.10 | 0.18 |
| 2 | 0.10 | 0.20 | 0.35 |
| 3 | 0.20 | 0.20 | 1.40 |
$${[NO]_0}$$ and $${[C{l_2}]_0}$$ are the initial concentrations and r0 is the initial reaction rate.
The overall order of the reaction is __________. (Round off to the Nearest Integer).
18
For the reaction C2H6 $$ \to $$ C2H4 + H2
the reaction enthalpy $$\Delta$$rH = __________ kJ mol$$-$$1. (Round off to the Nearest Integer).
[ Given : Bond enthalpies in kJ mol$$-$$1 : C-C : 347, C = C : 611; C-H : 414, H-H : 436 ]
the reaction enthalpy $$\Delta$$rH = __________ kJ mol$$-$$1. (Round off to the Nearest Integer).
[ Given : Bond enthalpies in kJ mol$$-$$1 : C-C : 347, C = C : 611; C-H : 414, H-H : 436 ]
19
__________ grams of 3-Hydroxy propanal (MW = 74) must be dehydrated to produce 7.8 g of acrolein (MW = 56) (C3H4O) if the percentage yield is 64. (Round off to the Nearest Integer).
[Given : Atomic masses : C : 12.0 u, H : 1.0 u, O : 16.0 u ]
[Given : Atomic masses : C : 12.0 u, H : 1.0 u, O : 16.0 u ]
20
A reaction of 0.1 mole of Benzylamine with bromomethane gave 23 g of Benzyl trimethyl ammonium bromide. The number of moles of bromomethane consumed in this reaction are n $$\times$$ 10$$-$$1, when n = __________. (Round off to the Nearest Integer).
(Given : Atomic masses : C : 12.0 u, H : 1.0 u, N : 14.0 u, Br : 80.0 u]
(Given : Atomic masses : C : 12.0 u, H : 1.0 u, N : 14.0 u, Br : 80.0 u]
21
The total number of unpaired electrons present in the complex K3[Cr(oxalate)3] is _____________.
22
2 molal solution of a weak acid HA has a freezing point of 3.885$$^\circ$$C. The degree of dissociation of this acid is ___________ $$\times$$ 10$$-$$3. (Round off to the Nearest Integer).
[Given : Molal depression constant of water = 1.85 K kg mol$$-$$1 Freezing point of pure water = 0$$^\circ$$ C]
[Given : Molal depression constant of water = 1.85 K kg mol$$-$$1 Freezing point of pure water = 0$$^\circ$$ C]
23
For the reaction
2Fe3+(aq) + 2I$$-$$(aq) $$ \to $$ 2Fe2+(aq) + I2(s)
the magnitude of the standard molar Gibbs free energy change, $$\Delta$$rG$$_m^o$$ = $$-$$ ___________ kJ (Round off to the Nearest Integer).
$$\left[ {\matrix{ {E_{F{e^{2 + }}/Fe(s)}^o = - 0.440V;} & {E_{F{e^{3 + }}/Fe(s)}^o = - 0.036V} \cr {E_{{I_2}/2{I^ - }}^o = 0.539V;} & {F = 96500C} \cr } } \right]$$
2Fe3+(aq) + 2I$$-$$(aq) $$ \to $$ 2Fe2+(aq) + I2(s)
the magnitude of the standard molar Gibbs free energy change, $$\Delta$$rG$$_m^o$$ = $$-$$ ___________ kJ (Round off to the Nearest Integer).
$$\left[ {\matrix{ {E_{F{e^{2 + }}/Fe(s)}^o = - 0.440V;} & {E_{F{e^{3 + }}/Fe(s)}^o = - 0.036V} \cr {E_{{I_2}/2{I^ - }}^o = 0.539V;} & {F = 96500C} \cr } } \right]$$
24
Complete combustion of 3g of ethane gives x $$\times$$ 1022 molecules of water. The value of x is __________. (Round off to the Nearest Integer). [Use : NA = 6.023 $$\times$$ 1023; Atomic masses in u : C : 12.0; O : 16.0; H : 1.0]
Mathematics
1
The number of integral values of m so that the abscissa of point of intersection of lines 3x + 4y = 9 and y = mx + 1 is also an integer, is :
2
The solutions of the equation $$\left| {\matrix{
{1 + {{\sin }^2}x} & {{{\sin }^2}x} & {{{\sin }^2}x} \cr
{{{\cos }^2}x} & {1 + {{\cos }^2}x} & {{{\cos }^2}x} \cr
{4\sin 2x} & {4\sin 2x} & {1 + 4\sin 2x} \cr
} } \right| = 0,(0 < x < \pi )$$, are
3
Let $$\alpha$$, $$\beta$$, $$\gamma$$ be the real roots of the equation, x3 + ax2 + bx + c = 0, (a, b, c $$\in$$ R and a, b $$\ne$$ 0). If the system of equations (in u, v, w) given by $$\alpha$$u + $$\beta$$v + $$\gamma$$w = 0, $$\beta$$u + $$\gamma$$v + $$\alpha$$w = 0; $$\gamma$$u + $$\alpha$$v + $$\beta$$w = 0 has non-trivial solution, then the value of $${{{a^2}} \over b}$$ is
4
The integral $$\int {{{(2x - 1)\cos \sqrt {{{(2x - 1)}^2} + 5} } \over {\sqrt {4{x^2} - 4x + 6} }}} dx$$ is equal to (where c is a constant of integration)
5
The equation of one of the straight lines which passes through the point (1, 3) and makes an angles $${\tan ^{ - 1}}\left( {\sqrt 2 } \right)$$ with the straight line, y + 1 = 3$${\sqrt 2 }$$ x is :
6
If $$\mathop {\lim }\limits_{x \to 0} {{{{\sin }^{ - 1}}x - {{\tan }^{ - 1}}x} \over {3{x^3}}}$$ is equal to L, then the value of (6L + 1) is
7
A vector $$\overrightarrow a $$ has components 3p and 1 with respect to a rectangular cartesian system. This system is rotated through a certain angle about the origin in the counter clockwise sense. If, with respect to new system, $$\overrightarrow a $$ has components p + 1 and $$\sqrt {10} $$, then the value of p is equal to :
8
If the equation $$a|z{|^2} + \overline {\overline \alpha z + \alpha \overline z } + d = 0$$ represents a circle where a, d are real constants then which of the following condition is correct?
9
For the four circles M, N, O and P, following four equations are given :
Circle M : x2 + y2 = 1
Circle N : x2 + y2 $$-$$ 2x = 0
Circle O : x2 + y2 $$-$$ 2x $$-$$ 2y + 1 = 0
Circle P : x2 + y2 $$-$$ 2y = 0
If the centre of circle M is joined with centre of the circle N, further center of circle N is joined with centre of the circle O, centre of circle O is joined with the centre of circle P and lastly, centre of circle P is joined with centre of circle M, then these lines form the sides of a :
Circle M : x2 + y2 = 1
Circle N : x2 + y2 $$-$$ 2x = 0
Circle O : x2 + y2 $$-$$ 2x $$-$$ 2y + 1 = 0
Circle P : x2 + y2 $$-$$ 2y = 0
If the centre of circle M is joined with centre of the circle N, further center of circle N is joined with centre of the circle O, centre of circle O is joined with the centre of circle P and lastly, centre of circle P is joined with centre of circle M, then these lines form the sides of a :
10
The real valued function
$$f(x) = {{\cos e{c^{ - 1}}x} \over {\sqrt {x - [x]} }}$$, where [x] denotes the greatest integer less than or equal to x, is defined for all x belonging to :
$$f(x) = {{\cos e{c^{ - 1}}x} \over {\sqrt {x - [x]} }}$$, where [x] denotes the greatest integer less than or equal to x, is defined for all x belonging to :
11
If the functions are defined as $$f(x) = \sqrt x $$ and $$g(x) = \sqrt {1 - x} $$, then what is the common domain of the following functions :
f + g, f $$-$$ g, f/g, g/f, g $$-$$ f where $$(f \pm g)(x) = f(x) \pm g(x),(f/g)x = {{f(x)} \over {g(x)}}$$
f + g, f $$-$$ g, f/g, g/f, g $$-$$ f where $$(f \pm g)(x) = f(x) \pm g(x),(f/g)x = {{f(x)} \over {g(x)}}$$
12
If $$f(x) = \left\{ {\matrix{
{{1 \over {|x|}}} & {;\,|x|\, \ge 1} \cr
{a{x^2} + b} & {;\,|x|\, < 1} \cr
} } \right.$$ is differentiable at every point of the domain, then the values of a and b are respectively :
13
Let $$A + 2B = \left[ {\matrix{
1 & 2 & 0 \cr
6 & { - 3} & 3 \cr
{ - 5} & 3 & 1 \cr
} } \right]$$ and $$2A - B = \left[ {\matrix{
2 & { - 1} & 5 \cr
2 & { - 1} & 6 \cr
0 & 1 & 2 \cr
} } \right]$$. If Tr(A) denotes the sum of all diagonal elements of the matrix A, then Tr(A) $$-$$ Tr(B) has value equal to
14
The sum of all the 4-digit distinct numbers that can be formed with the digits 1, 2, 2 and 3 is :
15
The value of $$3 + {1 \over {4 + {1 \over {3 + {1 \over {4 + {1 \over {3 + ....\infty }}}}}}}}$$ is equal to
16
The number of times the digit 3 will be written when listing the integers from 1 to 1000 is :
17
Let f(x) and g(x) be two functions satisfying f(x2) + g(4 $$-$$ x) = 4x3 and g(4 $$-$$ x) + g(x) = 0, then the value of $$\int\limits_{ - 4}^4 {f{{(x)}^2}dx} $$ is
18
The missing value in the following figure is


19
Let z1, z2 be the roots of the equation z2 + az + 12 = 0 and z1, z2 form an equilateral triangle with origin. Then, the value of |a| is :
20
The mean age of 25 teachers in a school is 40 years. A teacher retires at the age of 60 years and a new teacher is appointed in his place. If the mean age of the teachers in this school now is 39 years, then the age (in years) of the newly appointed teacher is _________.
21
If $$f(x) = \int {{{5{x^8} + 7{x^6}} \over {{{({x^2} + 1 + 2{x^7})}^2}}}dx,(x \ge 0),f(0) = 0} $$ and $$f(1) = {1 \over K}$$, then the value of K is
22
A square ABCD has all its vertices on the curve x2y2 = 1. The midpoints of its sides also lie on the same curve. Then, the square of area of ABCD is _________.
Physics
1
An oil drop of radius 2 mm with a density 3g cm$$-$$3 is held stationary under a constant electric field 3.55 $$\times$$ 105 V m$$-$$1 in the Millikan's oil drop experiment. What is the number of excess electrons that the oil drop will possess? (consider g = 9.81 m/s2)
2
Imagine that the electron in a hydrogen atom is replaced by a muon ($$\mu$$). The mass of muon particle is 207 times that of an electron and charge is equal to the charge of an electron. The ionization potential of this hydrogen atom will be :
3
A plane electromagnetic wave of frequency 100 MHz is travelling in vacuum along the x-direction. At a particular point in space and time, $$\overrightarrow B = 2.0 \times {10^{ - 8}}\widehat kT$$. (where, $$\widehat k$$ is unit vector along z-direction) What is $$\overrightarrow E $$ at this point?
4
A thin circular ring of mass M and radius r is rotating about its axis with an angular speed $$\omega$$. Two particles having mass m each are now attached at diametrically opposite points. The angular speed of the ring will become :
5
Four identical long solenoids A, B, C and D are connected to each other as shown in the figure. If the magnetic field at the center of A is 3T, the field at the center of C would be : (Assume that the magnetic field is confined with in the volume of respective solenoid).
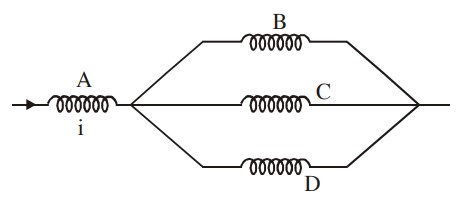

6
The P-V diagram of a diatomic ideal gas system going under cyclic process as shown in figure. The work done during an adiabatic process CD is (use $$\gamma$$ = 1.4) :


7
In Young's double slit arrangement, slits are separated by a gap of 0.5 mm, and the screen is placed at a distance of 0.5 m from them. The distance between the first and the third bright fringe formed when the slits are illuminated by a monochromatic light of 5890 $$\mathop A\limits^o $$ is :-
8
A particle is travelling 4 time as fast as an electron. Assuming the ratio of de-Broglie wavelength of a particle to that of electron is 2 : 1, the mass of the particle is :
9
The position, velocity and acceleration of a particle moving with a constant acceleration can be represented by :
10
In the experiment of Ohm's law, a potential difference of 5.0 V is applied across the end of a conductor of length 10.0 cm and diameter of 5.00 mm. The measured current in the conductor is 2.00 A. The maximum permissible percentage error in the resistivity of the conductor is :
11
In a series LCR resonance circuit, if we change the resistance only, from a lower to higher value :
12
An AC source rated 220 V, 50 Hz is connected to a resistor. The time taken by the current to change from its maximum to the rms value is :
13
Your friend is having eye sight problem. She is not able to see clearly a distant uniform window mesh and it appears to her as non-uniform and distorted. The doctor diagnosed the problem as :
14
A loop of flexible wire of irregular shape carrying current is placed in an external magnetic field. Identify the effect of the field on the wire.
15
The time period of a satellite in a circular orbit of radius R is T. The period of another satellite in a circular orbit of radius 9R is :
16
A particle performs simple harmonic motion with a period of 2 second. The time taken by the particle to cover a displacement equal to half of its amplitude from the mean position is $${1 \over a}$$s. The value of 'a' to the nearest integer is _________.
17
The circuit shown in the figure consists of a charged capacitor of capacity 3 $$\mu$$F and a charge of $$\mu$$C. At time t = 0, when the key is closed, the value of current flowing through the 5 M$$\Omega$$ resistor is 'x' $$\mu$$-A. The value of 'x to the nearest integer is ___________.


18
The voltage across the 10$$\Omega$$ resistor in the given circuit is x volt.

The value of 'x' to the nearest integer is _________.

The value of 'x' to the nearest integer is _________.
19
Two separate wires A and B are stretched by 2 mm and 4 mm respectively, when they are subjected to a force of 2 N. Assume that both the wires are made up of same material and the radius of wire B is 4 times that of the radius of wire A. The length of the wires A and B are in the ratio of a : b. Then a/b can be expressed as 1/x where x is _________.
20
A person is swimming with a speed of 10 m/s at an angle of 120$$^\circ$$ with the flow and reaches to a point directly opposite on the other side of the river. The speed of the flow is 'x' m/s. The value of 'x' to the nearest integer is __________.
21
A parallel plate capacitor has plate area 100 m2 and plate separation of 10 m. The space between the plates is filled up to a thickness 5 m with a material of dielectric constant of 10. The resultant capacitance of the system is 'x' pF.
The value of $$\varepsilon $$0 = 8.85 $$\times$$ 10$$-$$12 F.m$$-$$1.
The value of 'x' to the nearest integer is _____________.
The value of $$\varepsilon $$0 = 8.85 $$\times$$ 10$$-$$12 F.m$$-$$1.
The value of 'x' to the nearest integer is _____________.
22
A ball of mass 10 kg moving with a velocity 10$$\sqrt 3 $$ m/s along the x-axis, hits another ball of mass 20 kg which is at rest. After the collision, first ball comes to rest while the second ball disintegrates into two equal pieces. One piece starts moving along y-axis with a speed of 10 m/s. The second piece starts moving at an angle of 30$$^\circ$$ with respect to the x-axis. The velocity of the ball moving at 30$$^\circ$$ with x-axis is x m/s. The configuration of pieces after collision is shown in the figure below. The value of x to the nearest integer is ____________.


23
As shown in the figure, a particle of mass 10 kg is placed at a point A. When the particle is slightly displaced to its right, it starts moving and reaches the point B. The speed of the particle at B is x m/s. (Take g = 10 m/s2)
The value of 'x' to the nearest integer is __________.
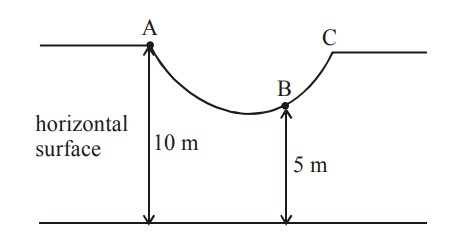
The value of 'x' to the nearest integer is __________.

24
A bullet of mass 0.1 kg is fired on a wooden block to pierce through it, but it stops after moving a distance of 50 cm into it. If the velocity of bullet before hitting the wood is 10 m/s and it slows down with uniform deceleration, then the magnitude of effective retarding force on the bullet is 'x' N. The value of 'x' to the nearest integer is __________.
25
The time period of a simple pendulum is given by $$T = 2\pi \sqrt {{l \over g}} $$. The measured value of the length of pendulum is 10 cm known to a 1mm accuracy. The time for 200 oscillations of the pendulum is found to be 100 second using a clock of 1s resolution. The percentage accuracy in the determination of 'g' using this pendulum is 'x'. The value of 'x' to be nearest integer is :-
26
A constant power delivering machine has towed a box, which was initially at rest, along a horizontal straight line. The distance moved by the box in time 't' is proportional to :-
27
What will be the average value of energy along one degree of freedom for an ideal gas in thermal equilibrium at a temperature T? (kB is Boltzmann constant)