JEE Main 2020 (Online) 5th September Morning Slot
Paper was held on
Sat, Sep 5, 2020 3:30 AM
Chemistry
1
The increasing order of the acidity of the $$\alpha $$-hydrogen of the following compounds is :
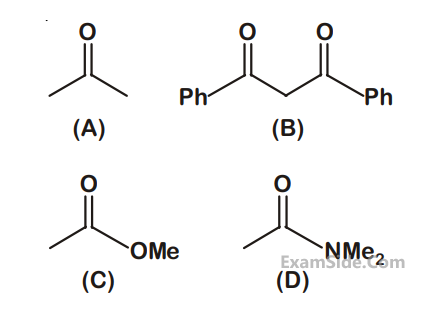

2
A flask contains a mixture of compounds A and
B. Both compounds decompose by first-order
kinetics. The half-lives for A and B are 300 s
and 180 s, respectively. If the concentrations
of A and B are equal initially, the time required
for the concentration of A to be four times that
of B(in s) :
(Use ln 2 = 0.693)
(Use ln 2 = 0.693)
3
The increasing order of basicity of the following
compounds is :
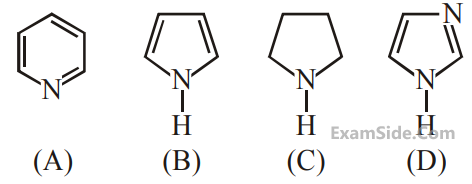

4
The difference between the radii of 3rd and 4th
orbits of Li2+ is R1 . The difference between the
radii of 3rd and 4th orbits of He+ is $$\Delta $$R2 .
Ratio $$\Delta $$R1 : $$\Delta $$R2 is :
orbits of Li2+ is R1 . The difference between the
radii of 3rd and 4th orbits of He+ is $$\Delta $$R2 .
Ratio $$\Delta $$R1 : $$\Delta $$R2 is :
5
The structure of PCl5
in the solid state is :
6
The most appropriate reagent for conversion of
C2H5CN into CH3CH2CH2NH2 is
7
Which of the following derivatives of alcohols
is unstable in an aqueous base?
8
The correct electronic configuration and spin-only
magnetic moment (BM) of Gd3+ (Z = 64), respectively, are :
magnetic moment (BM) of Gd3+ (Z = 64), respectively, are :
9
In the following reaction sequence the major
products A and B are :
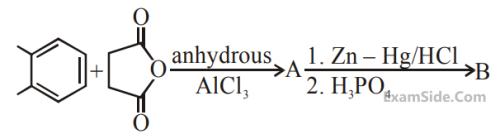
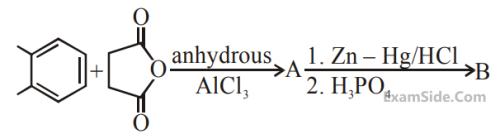
10
Which of the following is not an essential
amino acid :
11
Consider the following reaction:
N2O4(g) ⇌ 2NO2(g); $$\Delta $$Ho = +58 kJ
For each of the following cases (a, b), the direction in which the equilibrium shifts is :
(a) Temperature is decreased.
(b) Pressure is increased by adding N2 at constant T.
N2O4(g) ⇌ 2NO2(g); $$\Delta $$Ho = +58 kJ
For each of the following cases (a, b), the direction in which the equilibrium shifts is :
(a) Temperature is decreased.
(b) Pressure is increased by adding N2 at constant T.
12
The values of the crystal field stabilization
energies for a high spin d6 metal ion in
octahedral and tetrahedral fields, respectively,
are :
13
The total number of coordination sites
in ethylenediaminetetraacetate (EDTA4–) is _____.
in ethylenediaminetetraacetate (EDTA4–) is _____.
14
A soft drink was bottled with a partial pressure of CO2
of 3 bar over the liquid at room temperature.
The partial pressure of CO2
over the solution approaches a value of 30 bar when 44 g of CO2
is
dissolved in 1 kg of water at room temperature. The approximate pH of the soft drink is ______ $$ \times $$ 10–1.
(First dissociation constant of
H2CO3 = 4.0 $$ \times $$ 10–7; log 2 = 0.3; density
of the soft drink = 1 g mL–1) .
(First dissociation constant of
H2CO3 = 4.0 $$ \times $$ 10–7; log 2 = 0.3; density
of the soft drink = 1 g mL–1) .
15
An oxidation-reduction reaction in which
3 electrons are transferred has a $$\Delta $$Gº of 17.37 kJ mol–1 at
25 oC. The value of Eo
cell (in V) is ______ × 10–2.
(1 F = 96,500 C mol–1)
3 electrons are transferred has a $$\Delta $$Gº of 17.37 kJ mol–1 at
25 oC. The value of Eo
cell (in V) is ______ × 10–2.
(1 F = 96,500 C mol–1)
16
The number of chiral carbon(s) present in
peptide, Ile-Arg-Pro, is _____.
peptide, Ile-Arg-Pro, is _____.
17
The minimum number of moles of O2
required for complete combustion of 1 mole of propane and 2
moles of butane is _____.
18
The potential energy curve for the H2
molecule as a function of internuclear distance is :
19
In the sixth period, the orbitals that are filled are :
Mathematics
1
The number of words, with or without meaning, that can be formed by taking 4 letters at a time from the letters of the word ’SYLLABUS’ such that two letters are distinct and two letters are alike, is :
2
If the line, 2x - y + 3 = 0 is at a distance
$${1 \over {\sqrt 5 }}$$ and $${2 \over {\sqrt 5 }}$$ from the lines 4x - 2y + $$\alpha $$ = 0
and 6x - 3y + $$\beta $$ = 0, respectively, then the sum of all possible values of $$\alpha $$ and $$\beta $$ is :
$${1 \over {\sqrt 5 }}$$ and $${2 \over {\sqrt 5 }}$$ from the lines 4x - 2y + $$\alpha $$ = 0
and 6x - 3y + $$\beta $$ = 0, respectively, then the sum of all possible values of $$\alpha $$ and $$\beta $$ is :
3
The natural number m, for which the coefficient of x in the binomial expansion of
$${\left( {{x^m} + {1 \over {{x^2}}}} \right)^{22}}$$ is 1540, is .............
$${\left( {{x^m} + {1 \over {{x^2}}}} \right)^{22}}$$ is 1540, is .............
4
If $$\alpha $$ is positive root of the equation, p(x) = x2 - x - 2 = 0, then
$$\mathop {\lim }\limits_{x \to {\alpha ^ + }} {{\sqrt {1 - \cos \left( {p\left( x \right)} \right)} } \over {x + \alpha - 4}}$$ is equal to :
$$\mathop {\lim }\limits_{x \to {\alpha ^ + }} {{\sqrt {1 - \cos \left( {p\left( x \right)} \right)} } \over {x + \alpha - 4}}$$ is equal to :
5
If
$$\int {\left( {{e^{2x}} + 2{e^x} - {e^{ - x}} - 1} \right){e^{\left( {{e^x} + {e^{ - x}}} \right)}}dx} $$ = $$g\left( x \right){e^{\left( {{e^x} + {e^{ - x}}} \right)}} + c$$
where c is a constant of integration, then g(0) is equal to :
$$\int {\left( {{e^{2x}} + 2{e^x} - {e^{ - x}} - 1} \right){e^{\left( {{e^x} + {e^{ - x}}} \right)}}dx} $$ = $$g\left( x \right){e^{\left( {{e^x} + {e^{ - x}}} \right)}} + c$$
where c is a constant of integration, then g(0) is equal to :
6
Four fair dice are thrown independently 27 times. Then the expected number of times, at
least two dice show up a three or a five, is _________.
7
If the co-ordinates of two points A and B
are $$\left( {\sqrt 7 ,0} \right)$$ and $$\left( { - \sqrt 7 ,0} \right)$$ respectively and
P is any point on the conic, 9x2 + 16y2 = 144, then PA + PB is equal to :
are $$\left( {\sqrt 7 ,0} \right)$$ and $$\left( { - \sqrt 7 ,0} \right)$$ respectively and
P is any point on the conic, 9x2 + 16y2 = 144, then PA + PB is equal to :
8
Let $$f(x) = x.\left[ {{x \over 2}} \right]$$, for -10< x < 10, where [t] denotes the greatest integer function. Then the number of points of discontinuity of f is equal to _____.
9
Let $$\lambda \in $$ R . The system of linear equations
2x1 - 4x2 + $$\lambda $$x3 = 1
x1 - 6x2 + x3 = 2
$$\lambda $$x1 - 10x2 + 4x3 = 3
is inconsistent for:
2x1 - 4x2 + $$\lambda $$x3 = 1
x1 - 6x2 + x3 = 2
$$\lambda $$x1 - 10x2 + 4x3 = 3
is inconsistent for:
10
If $${3^{2\sin 2\alpha - 1}}$$, 14 and $${3^{4 - 2\sin 2\alpha }}$$ are the first three terms of an A.P. for some $$\alpha $$, then the sixth
terms of this A.P. is:
11
If the minimum and the maximum values of the function $$f:\left[ {{\pi \over 4},{\pi \over 2}} \right] \to R$$, defined by
$$f\left( \theta \right) = \left| {\matrix{ { - {{\sin }^2}\theta } & { - 1 - {{\sin }^2}\theta } & 1 \cr { - {{\cos }^2}\theta } & { - 1 - {{\cos }^2}\theta } & 1 \cr {12} & {10} & { - 2} \cr } } \right|$$ are m and M respectively, then the ordered pair (m,M) is equal to :
$$f\left( \theta \right) = \left| {\matrix{ { - {{\sin }^2}\theta } & { - 1 - {{\sin }^2}\theta } & 1 \cr { - {{\cos }^2}\theta } & { - 1 - {{\cos }^2}\theta } & 1 \cr {12} & {10} & { - 2} \cr } } \right|$$ are m and M respectively, then the ordered pair (m,M) is equal to :
12
A survey shows that 73% of the persons working in an office like coffee, whereas 65% like tea. If x denotes the percentage of them, who like both coffee and tea, then x cannot be :
13
The mean and variance of 7 observations are 8 and 16, respectively. If five observations are 2, 4, 10, 12, 14, then the absolute difference of the remaining two observations is :
14
If the point P on the curve, 4x2 + 5y2 = 20 is
farthest from the point Q(0, -4), then PQ2 is equal to:
farthest from the point Q(0, -4), then PQ2 is equal to:
15
If the four complex numbers $$z,\overline z ,\overline z - 2{\mathop{\rm Re}\nolimits} \left( {\overline z } \right)$$ and $$z-2Re(z)$$ represent the vertices of a square of
side 4 units in the Argand plane, then $$|z|$$ is equal to :
16
If the function
$$f\left( x \right) = \left\{ {\matrix{ {{k_1}{{\left( {x - \pi } \right)}^2} - 1,} & {x \le \pi } \cr {{k_2}\cos x,} & {x > \pi } \cr } } \right.$$ is
twice differentiable, then the ordered pair (k1, k2) is equal to :
$$f\left( x \right) = \left\{ {\matrix{ {{k_1}{{\left( {x - \pi } \right)}^2} - 1,} & {x \le \pi } \cr {{k_2}\cos x,} & {x > \pi } \cr } } \right.$$ is
twice differentiable, then the ordered pair (k1, k2) is equal to :
17
If (a, b, c) is the image of the point (1, 2, -3) in
the line $${{x + 1} \over 2} = {{y - 3} \over { - 2}} = {z \over { - 1}}$$, then a + b + c is :
the line $${{x + 1} \over 2} = {{y - 3} \over { - 2}} = {z \over { - 1}}$$, then a + b + c is :
18
The value of $$\int\limits_{{{ - \pi } \over 2}}^{{\pi \over 2}} {{1 \over {1 + {e^{\sin x}}}}dx} $$ is:
19
If S is the sum of the first 10 terms of the series
$${\tan ^{ - 1}}\left( {{1 \over 3}} \right) + {\tan ^{ - 1}}\left( {{1 \over 7}} \right) + {\tan ^{ - 1}}\left( {{1 \over {13}}} \right) + {\tan ^{ - 1}}\left( {{1 \over {21}}} \right) + ....$$
then tan(S) is equal to :
$${\tan ^{ - 1}}\left( {{1 \over 3}} \right) + {\tan ^{ - 1}}\left( {{1 \over 7}} \right) + {\tan ^{ - 1}}\left( {{1 \over {13}}} \right) + {\tan ^{ - 1}}\left( {{1 \over {21}}} \right) + ....$$
then tan(S) is equal to :
20
If y = y(x) is the solution of the differential
equation $${{5 + {e^x}} \over {2 + y}}.{{dy} \over {dx}} + {e^x} = 0$$ satisfying y(0) = 1, then a value of y(loge13) is :
equation $${{5 + {e^x}} \over {2 + y}}.{{dy} \over {dx}} + {e^x} = 0$$ satisfying y(0) = 1, then a value of y(loge13) is :
21
The product of the roots of the
equation 9x2 - 18|x| + 5 = 0 is :
equation 9x2 - 18|x| + 5 = 0 is :
Physics
1
A particle of mass 200 MeV/c2 collides with a
hydrogen atom at rest. Soon after the collision
the particle comes to rest, and the atom
recoils and goes to its first excited state. The
initial kinetic energy of the particle (in eV) is
$${N \over 4}$$. The value of N is :
(Given the mass of the hydrogen atom to be 1 GeV/c2) ______ .
$${N \over 4}$$. The value of N is :
(Given the mass of the hydrogen atom to be 1 GeV/c2) ______ .
2
A compound microscope consists of an
objective lens of focal length 1 cm and an
eyepiece of focal length 5 cm with a separation
of 10 cm.
The distance between an object and the objective lens, at which the strain on the eye is minimum is $${n \over {40}}$$ cm. The value of n is _____.
The distance between an object and the objective lens, at which the strain on the eye is minimum is $${n \over {40}}$$ cm. The value of n is _____.
3
A force $$\overrightarrow F = \left( {\widehat i + 2\widehat j + 3\widehat k} \right)$$ N acts at a point
$$\left( {4\widehat i + 3\widehat j - \widehat k} \right)$$ m. Then the magnitude of torque
about the point $$\left( {\widehat i + 2\widehat j + \widehat k} \right)$$ m will be $$\sqrt x $$ N m.
The value of x is _______.
$$\left( {4\widehat i + 3\widehat j - \widehat k} \right)$$ m. Then the magnitude of torque
about the point $$\left( {\widehat i + 2\widehat j + \widehat k} \right)$$ m will be $$\sqrt x $$ N m.
The value of x is _______.
4
With increasing biasing voltage of a photodiode,
the photocurrent magnitude :
5
A physical quantity z depends on four
observables
a, b, c and d, as z = $${{{a^2}{b^{{2 \over 3}}}} \over {\sqrt c {d^3}}}$$. The percentages of error in the measurement of a, b, c and d are 2%, 1.5%, 4% and 2.5% respectively. The percentage of error in z is :
a, b, c and d, as z = $${{{a^2}{b^{{2 \over 3}}}} \over {\sqrt c {d^3}}}$$. The percentages of error in the measurement of a, b, c and d are 2%, 1.5%, 4% and 2.5% respectively. The percentage of error in z is :
6
Two capacitors of capacitances C and 2C are
charged to potential differences V and 2V,
respectively. These are then connected in
parallel in such a manner that the positive
terminal of one is connected to the negative
terminal of the other. The final energy of this
configuration is :
7
A helicopter rises from rest on the ground
vertically upwards with a constant acceleration
g. A food packet is dropped from the helicopter
when it is at a height h. The time taken by the
packet to reach the ground is close to :
[g is the acceleration due to gravity]
[g is the acceleration due to gravity]
8
Assume that the displacement(s) of air is
proportional to the pressure difference ($$\Delta $$p)
created by a sound wave. Displacement (s)
further depends on the speed of sound (v),
density of air ($$\rho $$) and the frequency (f). If
$$\Delta $$p ~ 10 Pa, v ~ 300 m/s, $$\rho $$ ~ 1 kg/m3 and f ~ 1000 Hz,
then s will be of the order of (take the
multiplicative constant to be 1) :
9
A hollow spherical shell at outer radius R floats
just submerged under the water surface. The
inner radius of the shell is r. If the specific
gravity of the shell material is $${{27} \over 8}$$ w.r.t water,
the value of r is :
10
An electron is constrained to move along
the y-axis with a speed of 0.1 c (c is the
speed of light) in the presence of
electromagnetic wave, whose electric
field is
$$\overrightarrow E = 30\widehat j\sin \left( {1.5 \times {{10}^7}t - 5 \times {{10}^{ - 2}}x} \right)$$ V/m.
The maximum magnetic force experienced by the electron will be :
(given c = 3 $$ \times $$ 108 ms–1 and electron charge = 1.6 $$ \times $$ 10–19 C)
$$\overrightarrow E = 30\widehat j\sin \left( {1.5 \times {{10}^7}t - 5 \times {{10}^{ - 2}}x} \right)$$ V/m.
The maximum magnetic force experienced by the electron will be :
(given c = 3 $$ \times $$ 108 ms–1 and electron charge = 1.6 $$ \times $$ 10–19 C)
11
A wheel is rotating freely with an angular speed
$$\omega $$ on a shaft. The moment of inertia of the
wheel is I and the moment of inertia of the
shaft is negligible. Another wheel of moment of
inertia 3I initially at rest is suddenly coupled to
the same shaft. The resultant fractional loss in
the kinetic energy of the system is :
12
A bullet of mass 5 g, travelling with a speed of
210 m/s, strikes a fixed wooden target. One half
of its kinetic energy is converted into heat in
the bullet while the other half is converted into
heat in the wood. The rise of temperature of
the bullet if the specific heat of its material is
0.030 cal/(g – oC) (1 cal = 4.2 × 107 ergs) close
to :
13
For a concave lens of focal length f, the relation
between object and image distances u and v,
respectively, from its pole can best be
represented by (u = v is the reference line) :
14
Two concentric circular coils, C1 and C2 are
placed in the XY plane. C1 has 500 turns, and
a radius of 1 cm. C2 has 200 turns and radius
of 20 cm. C2 carries a time dependent current
I(t) = (5t2 – 2t + 3) A where t is in s. The emf
induced in C1 (in mV), at the instant t = 1 s is
$${4 \over x}$$. The value of x is ___ .
placed in the XY plane. C1 has 500 turns, and
a radius of 1 cm. C2 has 200 turns and radius
of 20 cm. C2 carries a time dependent current
I(t) = (5t2 – 2t + 3) A where t is in s. The emf
induced in C1 (in mV), at the instant t = 1 s is
$${4 \over x}$$. The value of x is ___ .
15
A square loop of side 2$$a$$, and carrying current
I, is kept in XZ plane with its centre at origin.
A long wire carrying the same current I is
placed parallel to the z-axis and passing
through the point (0, b, 0), (b >> a). The
magnitude of the torque on the loop about zaxis is given by :
16
Number of molecules in a volume of 4 cm3 of
a perfect monoatomic gas at some temperature
T and at a pressure of 2 cm of mercury is close
to?
(Given, mean kinetic energy of a molecule
(at T) is 4 $$ \times $$ 10–14 erg, g = 980 cm/s2, density of
mercury = 13.6 g/cm3)
(Given, mean kinetic energy of a molecule
(at T) is 4 $$ \times $$ 10–14 erg, g = 980 cm/s2, density of
mercury = 13.6 g/cm3)
17
A balloon is moving up in air vertically above a
point A on the ground. When it is at a height h1,
a girl standing at a distanced (point B) from A
(see figure) sees it at an angle 45o with respect
to the vertical. When the balloon climbs up a
further height h2, it is seen at an angle 60o with
respect to the vertical if the girl moves further
by a distance 2.464 d(point C). Then the height
h2 is (given tan 30o = 0.5774)
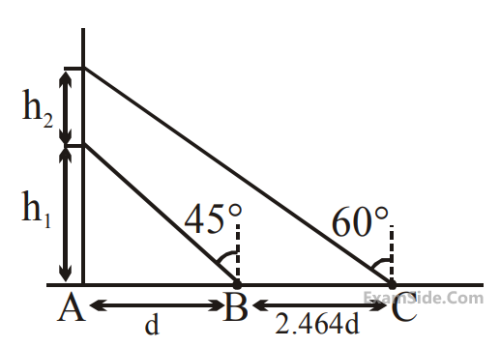

18
A galvanometer of resistance G is converted
into a voltmeter of range 0 – 1 V by connecting
a resistance R1 in series with it. The additional
resistance that should be connected in series
with R1 to increase the range of the voltmeter
to 0 – 2 V will be :
19
In a resonance tube experiment when the tube
is filled with water up to a height of 17.0 cm
from bottom, it resonates with a given tuning
fork. When the water level is raised the next
resonance with the same tuning fork occurs at
a height of 24.5 cm. If the velocity of sound in
air is 330 m/s, the tuning fork frequency is :
20
The value of the acceleration due to gravity is
g1 at a height h = $${R \over 2}$$ (R = radius of the earth) from the surface of the earth. It is again equal
to g1 at a depth d below the surface of the
earth. The ratio $$\left( {{d \over R}} \right)$$ equals :
21
An electrical power line, having a total
resistance of 2 $$\Omega $$, delivers 1 kW at 220 V. The
efficiency of the transmission line is
approximately :
22
A solid sphere of radius R carries a charge
Q + q distributed uniformly over its volume. A
very small point like piece of it of mass m gets
detached from the bottom of the sphere and
falls down vertically under gravity. This piece
carries charge q. If it acquires a speed v when
it has fallen through a vertical height y (see
figure), then :
(assume the remaining portion to be spherical).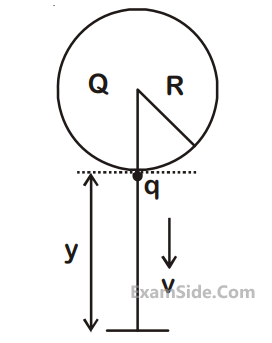
(assume the remaining portion to be spherical).

23
Three different processes that can occur in an
ideal monoatomic gas are shown in the P vs V
diagram. The paths are labelled as A $$ \to $$ B,
A $$ \to $$ C and A $$ \to $$ D. The change in internal
energies during these process are taken as
EAB, EAC and EAD and the work done as WAB,
WAC and WAD.
The correct relation between these parameters are :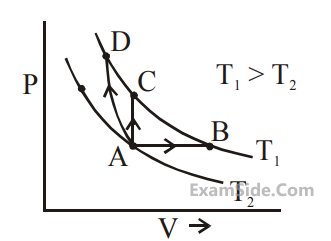
The correct relation between these parameters are :
