AIEEE 2005
Paper was held on
Thu, Apr 28, 2005 9:30 AM
Chemistry
1
An amount of solid NH4HS is placed in a flask already containing ammonia gas at a
certain temperature and 0.50 atm. Pressure. Ammonium hydrogen sulphide
decomposes to yield NH3 and H2S gases in the flask. When the decomposition
reaction reaches equilibrium, the total pressure in the flask rises to 0.84 atm. The
equilibrium constant for NH4HS decomposition at this temperature is :
2
Consider the reaction: N2 + 3H2 $$\to$$ 2NH3 carried out at constant temperature and
pressure. If $$\Delta H$$ and $$\Delta U$$ are the enthalpy and internal energy changes for the
reaction, which of the following expressions is true?
3
If the bond dissociation energies of XY, X2 and Y2 (all diatomic molecules) are in the ratio of 1:1:0.5 and $$\Delta H_f$$ for the formation of XY is -200 kJ mole-1. The bond
dissociation energy of X2 will be :
4
Consider an endothermic reaction, X $$\to$$ Y with the activation energies Eb and Ef
for the backward and forward reactions, respectively. In general :
5
If $$\alpha$$ is the degree of dissociation of Na2SO4, the vant Hoff’s factor (i) used for
calculating the molecular mass is :
6
The solubility product of a salt having general formula MX2, in water is: 4 $$\times$$ 10-12 . The
concentration of M2+ ions in the aqueous solution of the salt is :
7
The exothermic formation of ClF3 is represented by the equation:
Cl2 (g) + 3F2 (g) $$\leftrightharpoons$$ 2ClF3 (g); $$\Delta H$$ = -329 kJ
Which of the following will increase the quantity of ClF3 in an equilibrium mixture of Cl2, F2 and ClF3?
Cl2 (g) + 3F2 (g) $$\leftrightharpoons$$ 2ClF3 (g); $$\Delta H$$ = -329 kJ
Which of the following will increase the quantity of ClF3 in an equilibrium mixture of Cl2, F2 and ClF3?
8
For the reaction
2NO2 (g) $$\leftrightharpoons$$ 2NO (g) + O2 (g), (Kc = 1.8 $$\times$$ 10-6 at 184oC) (R = 0.0831 kJ/(mol. K))
When Kp and Kc are compared at 184oC , it is found that :
When Kp and Kc are compared at 184oC , it is found that :
9
What is the conjugate base of OH-?
10
Hydrogen ion concentration in mol / L in a solution of pH = 5.4 will be :
11
Which one of the following species is diamagnetic in nature?
12
Due to the presence of an unpaired electron, free radicals are:
13
Reaction of one molecule of HBr with one molecule of 1,3-butadiene at 40oC gives
predominantly
14
Of the five isomeric hexanes, the isomer which can give two monochlorinated
compounds is
15
2 methylbutane on reacting with bromine in the presence of sunlight gives mainly
16
Acid catalyzed hydration of alkenes except ethene leads to the formation of
17
Which types of isomerism is shown by 2,3-dichlorobutane?
18
Benzene and toluene form nearly ideal solutions. At 20 oC, the vapour pressure of
benzene is 75 torr and that of toluene is 22 torr. The partial vapour pressure of
benzene at 20 oC for a solution containing 78 g of benzene and 46 g of toluene in
torr is
19
Equimolar solutions in the same solvent have
20
Amongst the following the most basic compound is
21
Which one of the following methods is neither meant for the synthesis nor for
separation of amines?
22
An organic compound having molecular mass 60 is found to contain C = 20%, H =
6.67% and N = 46.67% while rest is oxygen. On heating it gives NH3 along with a
solid residue. The solid residue give violet colour with alkaline copper sulphate
solution. The compound is
23
In both DNA and RNA, heterocyclic base and phosphate ester linkages are at-
24
Reaction of cyclohexanone with dimethylamine in the presence of catalytic amount of
an acid forms a compound if water during the reaction is continuously removed. The
compound formed is generally known as
25
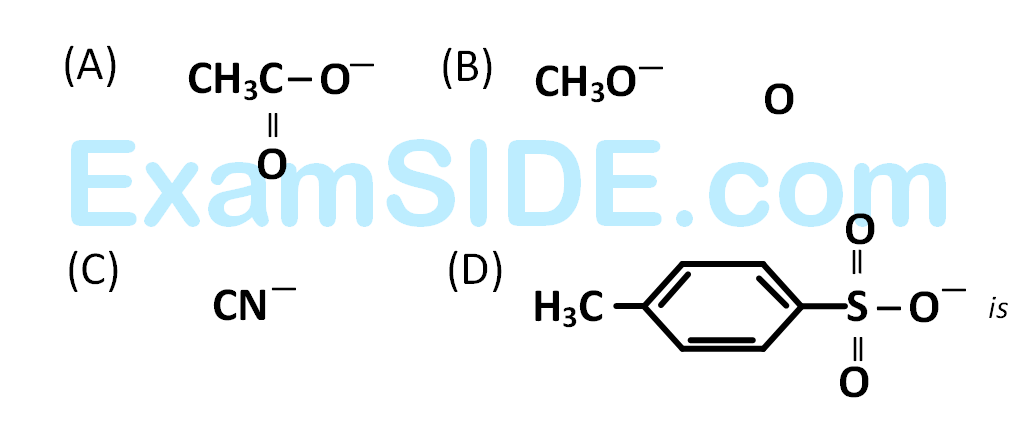
The decreasing order of nucleophilicity among the nucleophiles

26
The reaction

is fastest when $$X$$ is

is fastest when $$X$$ is
27
A schematic plot of $$ln$$ $${K_{eq}}$$ versus inverse of temperature for a reaction is shown below
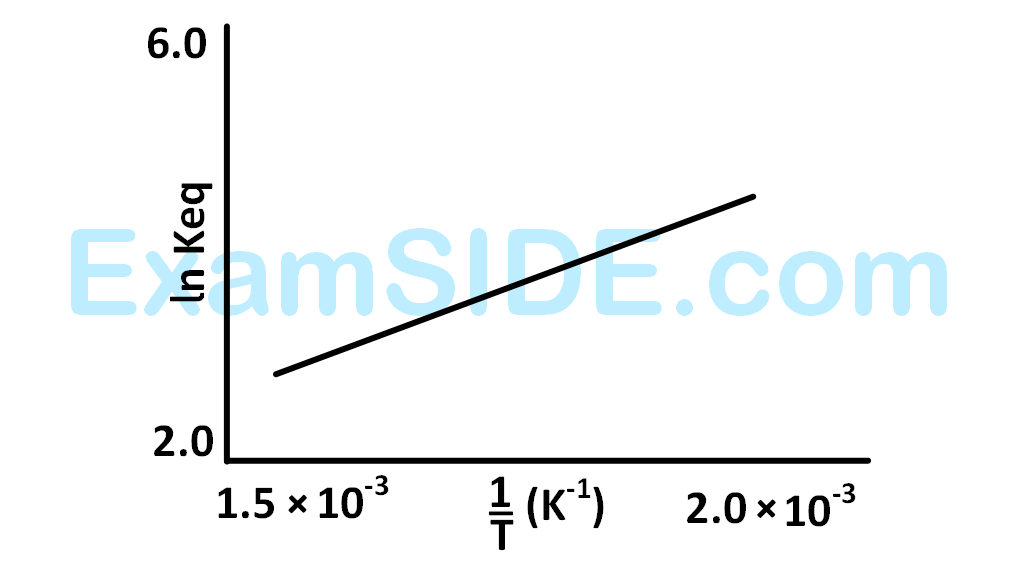
The reaction must be

The reaction must be
28
$$p$$-cresol reacts with chloroform in alkaline medium to give the compound A which adds hydrogen cyanide to form, the compound $$B.$$ The latter on acidic hydrolysis gives chiral carboxylic acid. The structure of the carboxylic acid is :
29
The oxidation state of chromium in the final product formed the reaction between $$K{\rm I}$$ and acidified potassium dichromate solution is :
30
On heating mixture of $$C{u_2}O$$ and $$C{u_2}S$$ will give :
31
Calomel $$\left( {H{g_2}C{l_2}} \right)$$ on reaction with ammonium hydroxide gives :
32
Pick out the isoelectronic structure from the following :
$$\eqalign{ & \left( i \right)\,\,\,\,\,\,C{H_3}^ + \cr & \left( {ii} \right)\,\,\,\,{H_3}{O^ + } \cr & \left( {iii} \right)\,\,\,N{H_3} \cr & \left( {iv} \right)\,\,\,\,C{H_3}^ - \cr} $$
$$\eqalign{ & \left( i \right)\,\,\,\,\,\,C{H_3}^ + \cr & \left( {ii} \right)\,\,\,\,{H_3}{O^ + } \cr & \left( {iii} \right)\,\,\,N{H_3} \cr & \left( {iv} \right)\,\,\,\,C{H_3}^ - \cr} $$
33
For a spontaneous reaction the ∆G , equilibrium constant (K) and $$E_{cell}^o$$ will be respectively
34
Aluminium oxide may be electrolysed at 1000oC to furnish aluminium metal (Atomic
mass = 27 amu; 1 Faraday = 96,500 Coulombs). The cathode reaction is Al3+ + 3e- $$\to$$ Alo To prepare 5.12 kg of aluminium metal by this method would require
35
The highest electrical conductivity of the following aqueous solutions is of :
36
| Electrolyte: | KCl | KNO3 | HCl | NaOAc | NaCl |
|---|---|---|---|---|---|
| $${ \wedge ^\infty }(Sc{m^2}mo{l^{ - 1}}):$$ |
149.9 | 145 | 426.2 | 91 | 126.5 |
37
Hydrogen bomb is based on the principle of
38
A reaction involving two different reactants can never be
39
The photon of hard gamma radiation knocks a proton out of $${}_{12}^{24}Mg$$ nucleus to form
40
t1/4 can be taken as the time taken for the concentration of a reactant to drop to $$3 \over 4$$ of its initial value. If the rate constant for a first order reaction is K, the t1/4 can be written as
41
The lanthanide contraction is responsible for the fact that :
42
Which of the following factors may be regarded as the main cause of lanthanide
contraction?
43
The IUPAC name of the coordination compound K3[Fe(CN)6] is
44
The oxidation state of Cr in [Cr(NH3)4Cl2]+ is :
45
Which of the following compounds shows optical isomerism?
46
The value of the ‘spin only’ magnetic moment for one of the following configurations
is 2.84 BM. The correct one is :
47
Which one of the following cyano complexes would exhibit the lowest value of
paramagnetic behaviour?
(At. No. Cr = 24, Mn = 25, Fe = 26, Co = 27)
(At. No. Cr = 24, Mn = 25, Fe = 26, Co = 27)
48
Tertiary alkyl halides are practically inert to substitution by SN2 mechanism because of
49
Elimination of bromine from 2-bromobutane results in the formation of-
50
Alkyl halides react with dialkyl copper reagents to give
51
The best reagent to convert pent -3- en-2-ol into pent -3-en-2-one is
52
Among the following acids which has the lowest pKa value?
53
Two solutions of a substance (non electrolyte) are mixed in the following manner. 480 ml of 1.5 M first solution + 520 ml of 1.2 M second solution. What is the molarity of the final mixture?
54
If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of the substance will
55
Of the following sets which one does NOT contain isoelectronic species?
56
In a multi-electron atom, which of the following orbitals described by the three quantum members will have the same energy in the absence of magnetic and electric fields?
(A) n = 1, l = 0, m = 0
(B) n = 2, l = 0, m = 0
(C) n = 2, l = 1, m = 1
(D) n = 3, l = 2, m = 1
(E) n = 3, l = 2, m = 0
(A) n = 1, l = 0, m = 0
(B) n = 2, l = 0, m = 0
(C) n = 2, l = 1, m = 1
(D) n = 3, l = 2, m = 1
(E) n = 3, l = 2, m = 0
57
Which of the following oxides is amphoteric in character?
58
In which of the following arrangements the order is NOT according to the property
indicated against it?
59
Lattice energy of an ionic compounds depends upon
Mathematics
1
Let $$f:( - 1,1) \to B$$, be a function defined by
$$f\left( x \right) = {\tan ^{ - 1}}{{2x} \over {1 - {x^2}}}$$,
then $$f$$ is both one-one and onto when B is the interval
$$f\left( x \right) = {\tan ^{ - 1}}{{2x} \over {1 - {x^2}}}$$,
then $$f$$ is both one-one and onto when B is the interval
2
A real valued function f(x) satisfies the functional equation
f(x - y) = f(x)f(y) - f(a - x)f(a + y)
where a is given constant and f(0) = 1, f(2a - x) is equal to
f(x - y) = f(x)f(y) - f(a - x)f(a + y)
where a is given constant and f(0) = 1, f(2a - x) is equal to
3
A function is matched below against an interval where it is supposed to be
increasing. Which of the following pairs is incorrectly matched?
4
Suppose $$f(x)$$ is differentiable at x = 1 and
$$\mathop {\lim }\limits_{h \to 0} {1 \over h}f\left( {1 + h} \right) = 5$$, then $$f'\left( 1 \right)$$ equals
$$\mathop {\lim }\limits_{h \to 0} {1 \over h}f\left( {1 + h} \right) = 5$$, then $$f'\left( 1 \right)$$ equals
5
Let $$\alpha$$ and $$\beta$$ be the distinct roots of $$a{x^2} + bx + c = 0$$, then
$$\mathop {\lim }\limits_{x \to \alpha } {{1 - \cos \left( {a{x^2} + bx + c} \right)} \over {{{\left( {x - \alpha } \right)}^2}}}$$ is equal to
$$\mathop {\lim }\limits_{x \to \alpha } {{1 - \cos \left( {a{x^2} + bx + c} \right)} \over {{{\left( {x - \alpha } \right)}^2}}}$$ is equal to
6
If $$f$$ is a real valued differentiable function satisfying
$$\left| {f\left( x \right) - f\left( y \right)} \right|$$ $$ \le {\left( {x - y} \right)^2}$$, $$x, y$$ $$ \in R$$
and $$f(0)$$ = 0, then $$f(1)$$ equals
$$\left| {f\left( x \right) - f\left( y \right)} \right|$$ $$ \le {\left( {x - y} \right)^2}$$, $$x, y$$ $$ \in R$$
and $$f(0)$$ = 0, then $$f(1)$$ equals
7
If in a frequency distribution, the mean and median are 21 and 22 respectively, then
its mode is approximately :
8
Let x1, x2,...........,xn be n observations such that
$$\sum {x_i^2} = 400$$ and $$\sum {{x_i}} = 80$$. Then a possible value of n among the following is
$$\sum {x_i^2} = 400$$ and $$\sum {{x_i}} = 80$$. Then a possible value of n among the following is
9
If the roots of the equation $${x^2} - bx + c = 0$$ be two consecutive integers, then $${b^2} - 4c$$ equals
10
The value of $$a$$ for which the sum of the squares of the roots of the equation $${x^2} - \left( {a - 2} \right)x - a - 1 = 0$$
assume the least value is :
11
If the cube roots of unity are 1, $$\omega \,,\,{\omega ^2}$$ then the roots of the equation $${(x - 1)^3}$$ + 8 = 0, are :
12
The value of $$\int\limits_{ - \pi }^\pi {{{{{\cos }^2}} \over {1 + {a^x}}}dx,\,\,a > 0,} $$ is
13
Area of the greatest rectangle that can be inscribed in the
ellipse $${{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1$$
ellipse $${{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1$$
14
A spherical iron ball $$10$$ cm in radius is coated with a layer of ice of uniform thickness that melts at a rate of $$50$$ cm$$^3$$ /min. When the thickness of ice is $$5$$ cm, then the rate at which the thickness of ice decreases is
15
If $${A^2} - A + 1 = 0$$, then the inverse of $$A$$ is :
16
The system of equations
$$\matrix{ {\alpha \,x + y + z = \alpha - 1} \cr {x + \alpha y + z = \alpha - 1} \cr {x + y + \alpha \,z = \alpha - 1} \cr } $$
has no solutions, if $$\alpha $$ is :
17
If $${a_1},{a_2},{a_3},........,{a_n},.....$$ are in G.P., then the determinant
$$$\Delta = \left| {\matrix{
{\log {a_n}} & {\log {a_{n + 1}}} & {\log {a_{n + 2}}} \cr
{\log {a_{n + 3}}} & {\log {a_{n + 4}}} & {\log {a_{n + 5}}} \cr
{\log {a_{n + 6}}} & {\log {a_{n + 7}}} & {\log {a_{n + 8}}} \cr
} } \right|$$$
is equal to :
is equal to :
18
If $${a^2} + {b^2} + {c^2} = - 2$$ and
f$$\left( x \right) = \left| {\matrix{ {1 + {a^2}x} & {\left( {1 + {b^2}} \right)x} & {\left( {1 + {c^2}} \right)x} \cr {\left( {1 + {a^2}} \right)x} & {1 + {b^2}x} & {\left( {1 + {c^2}} \right)x} \cr {\left( {1 + {a^2}} \right)x} & {\left( {1 + {b^2}} \right)x} & {1 + {c^2}x} \cr } } \right|,$$
then f$$(x)$$ is a polynomial of degree :
19
$$\int {{{\left\{ {{{\left( {\log x - 1} \right)} \over {1 + {{\left( {\log x} \right)}^2}}}} \right\}}^2}\,\,dx} $$ is equal to
20
If $${I_1} = \int\limits_0^1 {{2^{{x^2}}}dx,{I_2} = \int\limits_0^1 {{2^{{x^3}}}dx,\,{I_3} = \int\limits_1^2 {{2^{{x^2}}}dx} } } $$ and $${I_4} = \int\limits_1^2 {{2^{{x^3}}}dx} $$ then
21
The area enclosed between the curve $$y = {\log _e}\left( {x + e} \right)$$ and the coordinate axes is :
22
The parabolas $${y^2} = 4x$$ and $${x^2} = 4y$$ divide the square region bounded by the lines $$x=4,$$ $$y=4$$ and the coordinate axes. If $${S_1},{S_2},{S_3}$$ are respectively the areas of these parts numbered from top to bottom ; then $${S_1},{S_2},{S_3}$$ is :
23
Let $$f(x)$$ be a non - negative continuous function such that the area bounded by the curve $$y=f(x),$$ $$x$$-axis and the ordinates $$x = {\pi \over 4}$$ and $$x = \beta > {\pi \over 4}$$ is $$\left( {\beta \sin \beta + {\pi \over 4}\cos \beta + \sqrt 2 \beta } \right).$$ Then $$f\left( {{\pi \over 2}} \right)$$ is
24
If $${\cos ^{ - 1}}x - {\cos ^{ - 1}}{y \over 2} = \alpha ,$$ then $$4{x^2} - 4xy\cos \alpha + {y^2}$$ is equal to :
25
The value of integral, $$\int\limits_3^6 {{{\sqrt x } \over {\sqrt {9 - x} + \sqrt x }}} dx $$ is
26
The differential equation representing the family of curves $${y^2} = 2c\left( {x + \sqrt c } \right),$$ where $$c>0,$$ is a parameter, is of order and degree as follows:
27
If $$x{{dy} \over {dx}} = y\left( {\log y - \log x + 1} \right),$$ then the solution of the equation is :
28
Three houses are available in a locality. Three persons apply for the houses. Each applies for one house without consulting others. The probability that all the three apply for the same house is :
29
A random variable $$X$$ has Poisson distribution with mean $$2$$.
Then $$P\left( {X > 1.5} \right)$$ equals :
Then $$P\left( {X > 1.5} \right)$$ equals :
30
Let $$A$$ and $$B$$ two events such that $$P\left( {\overline {A \cup B} } \right) = {1 \over 6},$$ $$P\left( {A \cap B} \right) = {1 \over 4}$$ and $$P\left( {\overline A } \right) = {1 \over 4},$$ where $${\overline A }$$ stands for complement of event $$A$$. Then events $$A$$ and $$B$$ are :
31
If $$C$$ is the mid point of $$AB$$ and $$P$$ is any point outside $$AB,$$ then :
32
Let $$a, b$$ and $$c$$ be distinct non-negative numbers. If the vectors $$a\widehat i + a\widehat j + c\widehat k,\,\,\widehat i + \widehat k$$ and $$c\widehat i + c\widehat j + b\widehat k$$ lie in a plane, then $$c$$ is :
33
The angle between the lines $$2x=3y=-z$$ and $$6x=-y=-4z$$ is :
34
If a vertex of a triangle is $$(1, 1)$$ and the mid points of two sides through this vertex are $$(-1, 2)$$ and $$(3, 2)$$ then the centroid of the triangle is :
35
If $${z_1}$$ and $${z_2}$$ are two non-zero complex numbers such that $$\,\left| {{z_1} + {z_2}} \right| = \left| {{z_1}} \right| + \left| {{z_2}} \right|$$, then arg $${z_1}$$ - arg $${z_2}$$ is equal to :
36
If $$\,\omega = {z \over {z - {1 \over 3}i}}\,$$ and $$\left| \omega \right| = 1$$, then $$z$$ lies on :
37
In a triangle $$PQR,\;\;\angle R = {\pi \over 2}.\,\,If\,\,\tan \,\left( {{P \over 2}} \right)$$ and $$ \tan \left( {{Q \over 2}} \right)$$ are the roots of $$a{x^2} + bx + c = 0,\,\,a \ne 0$$ then
38
If both the roots of the quadratic equation $${x^2} - 2kx + {k^2} + k - 5 = 0$$ are less than 5, then $$k$$ lies in the interval
39
If the letter of the word SACHIN are arranged in all possible ways and these words are written out as in dictionary, then the word SACHIN appears at serial number
40
If the coefficient of $${x^7}$$ in $${\left[ {a{x^2} + \left( {{1 \over {bx}}} \right)} \right]^{11}}$$ equals the coefficient of $${x^{ - 7}}$$ in $${\left[ {ax - \left( {{1 \over {b{x^2}}}} \right)} \right]^{11}}$$, then $$a$$ and $$b$$ satisfy the relation
41
If $$x$$ is so small that $${x^3}$$ and higher powers of $$x$$ may be neglected, then $${{{{\left( {1 + x} \right)}^{{3 \over 2}}} - {{\left( {1 + {1 \over 2}x} \right)}^3}} \over {{{\left( {1 - x} \right)}^{{1 \over 2}}}}}$$ may be approximated as
42
If the coefficients of rth, (r+1)th, and (r + 2)th terms in the binomial expansion of $${{\rm{(1 + y )}}^m}$$ are in A.P., then m and r satisfy the equation
43
If $$x = \sum\limits_{n = 0}^\infty {{a^n},\,\,y = \sum\limits_{n = 0}^\infty {{b^n},\,\,z = \sum\limits_{n = 0}^\infty {{c^n},} } } \,\,$$ where a, b, c are in A.P and $$\,\left| a \right| < 1,\,\left| b \right| < 1,\,\left| c \right| < 1$$ then x, y, z are in
44
The line parallel to the $$x$$ - axis and passing through the intersection of the lines $$ax + 2by + 3b = 0$$ and $$bx - 2ay - 3a = 0,$$ where $$(a, b)$$ $$ \ne $$ $$(0, 0)$$ is :
45
If a circle passes through the point (a, b) and cuts the circle $${x^2}\, + \,{y^2} = {p^2}$$ orthogonally, then the equation of the locus of its centre is :
46
If the circles $${x^2}\, + \,{y^2} + \,2ax\, + \,cy\, + a\,\, = 0$$ and $${x^2}\, + \,{y^2} - \,3ax\, + \,dy\, - 1\,\, = 0$$ intersect in two ditinct points P and Q then the line 5x + by - a = 0 passes through P and Q for :
47
If the pair of lines $$a{x^2} + 2\left( {a + b} \right)xy + b{y^2} = 0$$ lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then :
48
An ellipse has $$OB$$ as semi minor axis, $$F$$ and $$F$$' its focii and theangle $$FBF$$' is a right angle. Then the eccentricity of the ellipse is :
49
Let $$P$$ be the point $$(1, 0)$$ and $$Q$$ a point on the parabola $${y^2} = 8x$$. The locus of mid point of $$PQ$$ is :
50
The value of $$a$$ for which the sum of the squares of the roots of the equation
$${x^2} - \left( {a - 2} \right)x - a - 1 = 0$$ assume the least value is
$${x^2} - \left( {a - 2} \right)x - a - 1 = 0$$ assume the least value is
51
Let $$f:R \to R$$ be a differentiable function having $$f\left( 2 \right) = 6$$,
$$f'\left( 2 \right) = \left( {{1 \over {48}}} \right)$$. Then $$\mathop {\lim }\limits_{x \to 2} \int\limits_6^{f\left( x \right)} {{{4{t^3}} \over {x - 2}}dt} $$ equals :
$$f'\left( 2 \right) = \left( {{1 \over {48}}} \right)$$. Then $$\mathop {\lim }\limits_{x \to 2} \int\limits_6^{f\left( x \right)} {{{4{t^3}} \over {x - 2}}dt} $$ equals :
52
If the roots of the equation $${x^2} - bx + c = 0$$ be two consecutive integers, then $${b^2} - 4c$$ equals
53
For any vector $${\overrightarrow a }$$ , the value of $${\left( {\overrightarrow a \times \widehat i} \right)^2} + {\left( {\overrightarrow a \times \widehat j} \right)^2} + {\left( {\overrightarrow a \times \widehat k} \right)^2}$$ is equal to :
54
If non zero numbers $$a, b, c$$ are in $$H.P.,$$ then the straight line $${x \over a} + {y \over b} + {1 \over c} = 0$$ always passes through a fixed point. That point is :
55
Let $R=\{(3,3),(6,6),(9,9),(12,12),(6,12)$, $(3,9),(3,12),(3,6)\}$ be a relation on the set $A=\{3,6,9,12\}$. The relation is :
56
A lizard, at an initial distance of 21 cm behind an insect moves from rest with an acceleration of $2 \mathrm{~cm} / \mathrm{s}^2$ and pursues the insect which is crawling uniformly along a straight line at a speed of $20 \mathrm{~cm} / \mathrm{s}$. Then the lizard will catch the insect after :
Physics
1
In a full wave rectifier circuit operating from $$50$$ $$Hz$$ mains frequency, the fundamental frequency in the ripple would be
2
A nuclear transformation is denoted by $$X\left( {n,\alpha } \right)\matrix{
7 \cr
3 \cr
} Li.$$ Which of the following is the nucleus of element $$X$$ ?
3
The diagram shows the energy levels for an electron in a certain atom. Which transition shown represents the emission of a photon with the most energy?
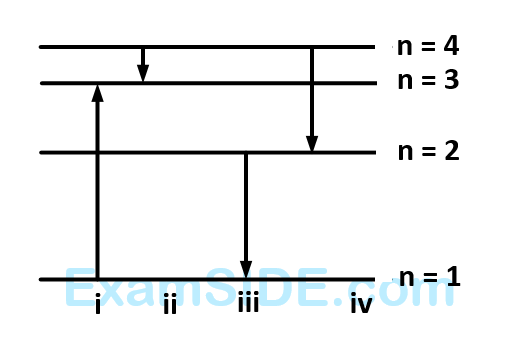

4
A photocell is illuminated by a small bright source placed $$1$$ $$m$$ away. When the same source of light is placed $${1 \over 2}$$ $$m$$ away, the number of electrons emitted by photo-cathode would
5
A fish looking up through the water sees the outside world contained in a circular horizon. If the refractive index of water is $${4 \over 3}$$ and the fish is $$12$$ $$cm$$ below the surface, the radius of this circle in $$cm$$ is
6
Two sources of equal $$emf$$ are connected to an external resistance $$R.$$ The internal resistance of the two sources are $${R_1}$$ and $${R_2}\left( {{R_1} > {R_1}} \right).$$ If the potential difference across the source having internal resistance $${R_2}$$ is zero, then
7
A moving coil galvanometer has $$150$$ equal divisions. Its current sensitivity is $$10$$- divisions per milliampere and voltage sensitivity is $$2$$ divisions per millivolt. In order that each division reads $$1$$ volt, the resistance in $$ohms$$ needed to be connected in series with the coil will be -
8
The resistance of hot tungsten filament is about $$10$$ times the cold resistance. What will be resistance of $$100$$ $$W$$ and $$200$$ $$V$$ lamp when not in use ?
9
An energy source will supply a constant current into the load if its internal resistance is
10
Two concentric coils each of radius equal to $$2$$ $$\pi $$ $$cm$$ are placed at right angles to each other. $$3$$ ampere and $$4$$ ampere are the currents flowing in each coil respectively . The magnetic induction in Weber / $${m^2}$$ at the center of the coils will be
$$\left( {\mu = 4\pi \times {{10}^{ - 7}}Wb/A.m} \right)$$
$$\left( {\mu = 4\pi \times {{10}^{ - 7}}Wb/A.m} \right)$$
11
A magnetic needle is kept in a non-uniform magnetic field. It experiences :
12
A uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected along the direction of the fields with a certain velocity then
13
A charged particle of mass $$m$$ and charge $$q$$ travels on a circular path of radius $$r$$ that is perpendicular to a magnetic field $$B.$$ The time taken by the particle to complete one revolution is
14
The self inductance of the motor of an electric fan is $$10$$ $$H$$. In order to impart maximum power at $$50$$ $$Hz$$, it should be connected to a capacitance of
15
A coil of inductance $$300$$ $$mH$$ and resistance $$2\,\Omega $$ is connected to a source of voltage $$2$$ $$V$$. The current reaches half of its steady state value in
16
A circuit has a resistance of $$12$$ $$ohm$$ and an impedance of $$15$$ $$ohm$$. The power factor of the circuit will be
17
The phase difference between the alternating current and $$emf$$ is $${\pi \over 2}.$$ Which of the following cannot be the constituent of the circuit?
18
Two point white dots are $$1$$ $$mm$$ apart on a black paper. They are viewed by eye of pupil diameter $$3$$ $$mm.$$ Approximately, what is the maximum distance at which these dots can be resolved by the eye? [ Take wavelength of light $$=500$$ $$nm$$ ]
19
A Young's double slit experiment uses a monochromatic source. The shape of the interference fringes formed on a screen is
20
A thin glass (refractive index $$1.5$$) lens has optical power of $$-5$$ $$D$$ in air. Its optical power in a liquid medium with refractive index $$1.6$$ will be
21
If $${I_0}$$ is the intensity of the principal maximum in the single slit diffraction pattern, then what will be its intensity when the slit width is doubled?
22
When an unpolarized light of intensity $${{I_0}}$$ is incident on a polarizing sheet, the intensity of the light which does not get transmitted is
23
One conducting $$U$$ tube can slide inside another as shown in figure, maintaining electrical contacts between the tubes. The magnetic field $$B$$ is perpendicular to the plane of the figure. If each tube moves towards the other at a constant speed $$v,$$ then the $$emf$$ induced in the circuit in terms of $$B,l$$ and $$v$$ where $$l$$ is the width of each tube, will be
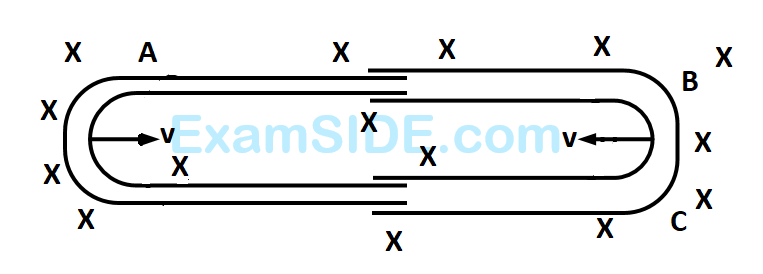

24
The electrical conductivity of a semiconductor increases when electromagnetic radiation of wavelength shorter than $$2480$$ $$nm$$ is incident on it. The band gap in $$(eV)$$ for the semiconductor is
25
If the kinetic energy of a free electron doubles, it's deBroglie wavelength changes by the factor
26
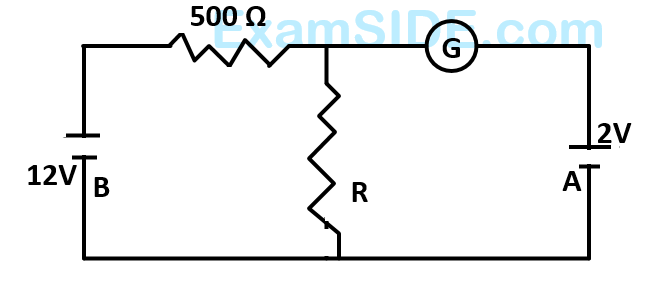
In the circuit, the galvanometer $$G$$ shows zero deflection. If the batteries $$A$$ and $$B$$ have negligible internal resistance, the value of the resistor $$R$$ will be -

27
Two simple harmonic motions are represented by the equations $${y_1} = 0.1\,\sin \left( {100\pi t + {\pi \over 3}} \right)$$ and $${y_2} = 0.1\,\cos \,\pi t.$$ The phase difference of the velocity of particle $$1$$ with respect to the velocity of particle $$2$$ is
28
Average density of the earth
29
If $$S$$ is stress and $$Y$$ is young's modulus of material of a wire, the energy stored in the wire per unit volume is
30
A $$20$$ $$cm$$ long capillary tube is dipped in water. The water rises up to $$8$$ $$cm.$$ If the entire arrangement is put in a freely falling elevator the length of water column in the capillary tube will be
31
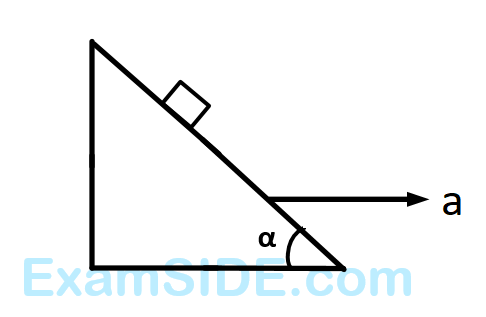
A block is kept on a frictionless inclined surface with angle of inclination $$'\,\alpha \,'.$$ The incline is given an acceleration $$a$$ to keep the block stationary. Then $$a$$ is equal to

32
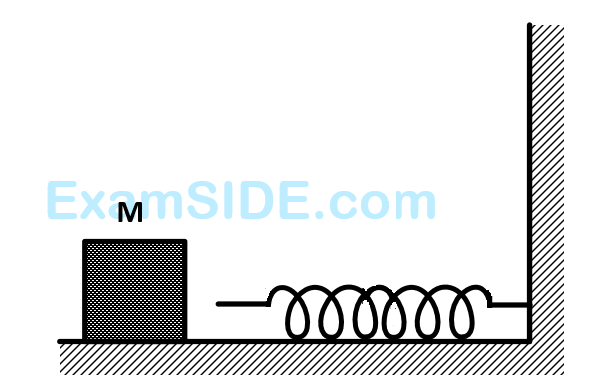
The block of mass $$M$$ moving on the frictionless horizontal surface collides with the spring of spring constant $$k$$ and compresses it by length $$L.$$ The maximum momentum of the block after collision is

33
A mass $$'m'$$ moves with a velocity $$'v'$$ and collides inelastically with another identical mass. After collision the $${1^{st}}$$ mass moves with velocity $${v \over {\sqrt 3 }}$$ in a direction perpendicular to the initial direction of motion. Find the speed of the $${2^{nd}}$$ mass after collision.
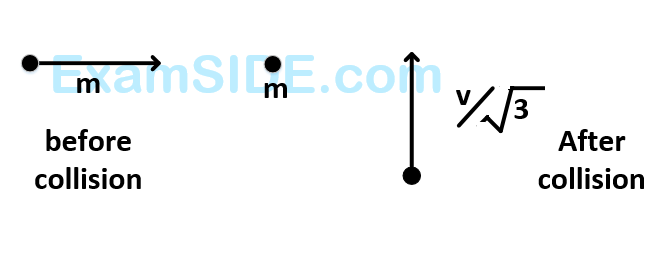
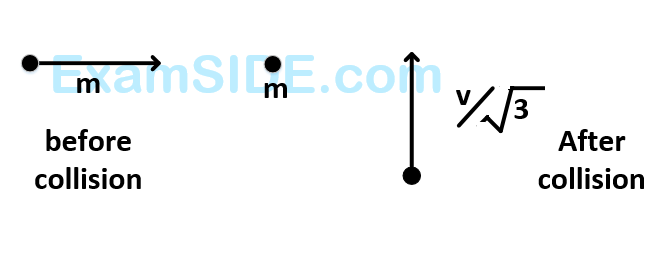
34
A gaseous mixture consists of $$16$$ $$g$$ of helium and $$16$$ $$g$$ of oxygen. The ratio $${{Cp} \over {{C_v}}}$$ of the mixture is
35
Which of the following is incorrect regarding the first law of thermodynamics?
36
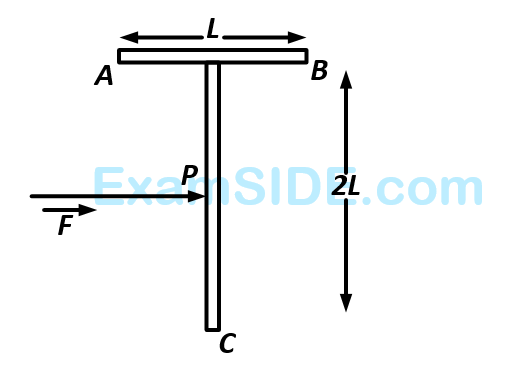
A T shaped object with dimensions shown in the figure, is lying on a smooth floor. A force $$'\,\,\overrightarrow F \,\,'$$ is applied at the point $$P$$ parallel to $$AB,$$ such that the object has only the translational motion without rotation. Find the location of $$P$$ with respect to $$C.$$

37
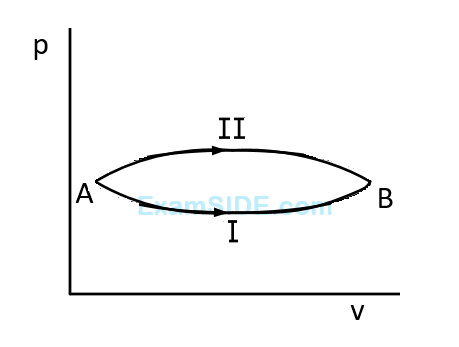
A system goes from $$A$$ to $$B$$ via two processes $$I$$ and $$II$$ as shown in figure. If $$\Delta {U_1}$$ and $$\Delta {U_2}$$ are the changes in internal energies in the processes $$I$$ and $$II$$ respectively, then

38
The figure shows a system of two concentric spheres of radii $${r_1}$$ and $${r_2}$$ are kept at temperatures $${T_1}$$ and $${T_2}$$, respectively. The radial rate of flow of heat in a substance between the two concentric spheres is proportional to


39
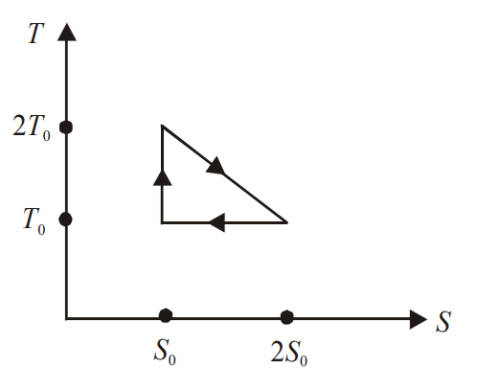
The temperature-entropy diagram of a reversible engine cycle is given in the figure. Its efficiency is

40
The function $${\sin ^2}\left( {\omega t} \right)$$ represents
41
The bob of a simple pendulum is a spherical hollow ball filled with water. A plugged hole near the bottom of the oscillating bob gets suddenly unplugged. During observation, till water is coming out, the time period of oscillation would
42
If a simple harmonic motion is represented by $${{{d^2}x} \over {d{t^2}}} + \alpha x = 0.$$ its time period is
43
When two tuning forks (fork $$1$$ and fork $$2$$) are sounded simultaneously, $$4$$ beats per second are heated. Now, some tape is attached on the prong of the fork $$2.$$ When the tuning forks are sounded again, $$6$$ beats per second are heard. If the frequency of fork $$1$$ is $$200$$ $$Hz$$, then what was the original frequency of fork $$2$$ ?
44
Two point charges $$+8q$$ and $$-2q$$ are located at $$x=0$$ and $$x=L$$ respectively. The location of a point on the $$x$$ axis at which the net electric field due to these two point charges is zero is
45
A parallel plate capacitor is made by stacking $$n$$ equally spaced plates connected alternatively. If the capacitance between any two adjacent plates is $$'C'$$ then the resultant capacitance is
46
Two thin wire rings each having a radius $$R$$ are placed at a distance $$d$$ apart with their axes coinciding. The charges on the two rings are $$+q$$ and $$-q.$$ The potential difference between the centres of the two rings is
47
A charged ball $$B$$ hangs from a silk thread $$S,$$ which makes angle $$\theta $$ with a large charged conducting sheet $$P,$$ as shown in the figure. The surface charge density $$\sigma $$ of the sheet is proportional to
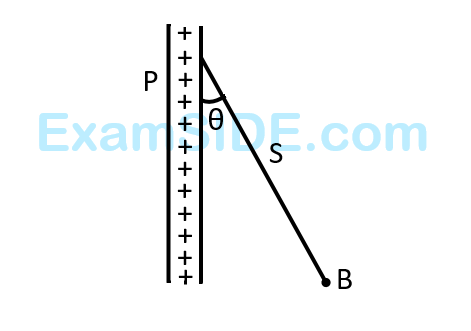 f
f
 f
f 48
A fully charged capacitor has a capacitance $$'C'$$. It is discharged through a small coil of resistance wire embedded in a thermally insulated block of specific heat capacity $$'s'$$ and mass $$'m'.$$ If the temperature of the block is raised by $$'\Delta T',$$ the potential difference $$'v'$$ across the capacitance is
49
Two thin, long, parallel wires, separated by a distance $$'d'$$ carry a current of $$'i'$$ $$A$$ in the same direction. They will
50
A heater coil is cut into two equal parts and only one part is now used in the heater. The heat generated will now be
51
Two voltmeters, one of copper and another of silver, are joined in parallel. When a total charge $$q$$ flows through the voltmeters, equal amount of metals are deposited. If the electrochemical equivalents of copper and silver are $${Z_1}$$ and $${Z_2}$$ respectively the charge which flows through the silver voltmeter is
52
A particle of mass $$10$$ $$g$$ is kept on the surface of a uniform sphere of mass $$100$$ $$kg$$ and radius $$10$$ $$cm.$$ Find the work to be done against the gravitational force between them to take the particle far away from the sphere (you may take $$G$$ $$ = 6.67 \times {10^{ - 11}}\,\,N{m^2}/k{g^2}$$)
53
Out of the following pair, which one does NOT have identical dimensions is
54
A car starting from rest accelerates at the rate f through a distance S, then continues
at constant speed for time t and then decelerates at the rate $${f \over 2}$$ to come to rest. If the
total distance traversed is 15 S, then
55
The relation between time t and distance x is t = ax2 + bx where a and b are constants.
The acceleration is
56
A particle is moving eastwards with a velocity of 5 m/s. In 10 seconds the velocity
changes to 5 m/s northwards. The average acceleration in this time is
57
A parachutist after bailing out falls $$50$$ $$m$$ without friction. When parachute opens, it decelerates at $$2\,\,m/{s^2}.$$ He reaches the ground with a speed of $$3$$ $$m/s$$. At what height, did he bail out?
58
A bullet fired into a fixed target loses half of its velocity after penetrating $$3$$ $$cm.$$ How much further it will penetrate before coming to rest assuming that it faces constant resistance to motion?
59
A smooth block is released at rest on a $${45^ \circ }$$ incline and then slides a distance $$'d'$$. The time taken to slide is $$'n'$$ times as much to slide on rough incline than on a smooth incline. The coefficient of friction is
60
A particle of mass 0.3 kg subjected to a force $$F=-kx$$ with $$k=15$$ $$N/m$$. What will be its initial acceleration if it is released from a point 20 cm away from the origin?
61
Consider a car moving on a straight road with a speed of $$100$$ $$m/s$$. The distance at which car can be stopped is $$\left[ {{\mu _k} = 0.5} \right]$$
62
An annular ring with inner and outer radii $${R_1}$$ and $${R_2}$$ is rolling without slipping with a uniform angular speed. The ratio of the forces experienced by the two particles situated on the inner and outer parts of the ring, $${{{F_1}} \over {{F_2}}}\,$$ is
63
The upper half of an inclined plane with inclination $$\phi $$ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
64
A body of mass $$m$$ is accelerated uniformly from rest to a speed $$v$$ in a time $$T.$$ The instantaneous power delivered to the body as a function of time is given by
65
A spherical ball of mass $$20$$ $$kg$$ is stationary at the top of a hill of height $$100$$ $$m$$. It rolls down a smooth surface to the ground, then climbs up another hill of height $$30$$ $$m$$ and finally rolls down to a horizontal base at a height of $$20$$ $$m$$ above the ground. The velocity attained by the ball is
66
The moment of inertia of a uniform semicircular disc of mass $$M$$ and radius $$r$$ about a line perpendicular to the plane of the disc through the center is
67
A body $$A$$ of mass $$M$$ while falling vertically downloads under gravity breaks into two-parts; a body $$B$$ of mass $${1 \over 3}$$ $$M$$ and a body $$C$$ of mass $${2 \over 3}$$ $$M.$$ The center of mass of bodies $$B$$ and $$C$$ taken together shifts compared to that of bodies $$B$$ and $$C$$ taken together shifts compared to that of body $$A$$ towards
68
The change in the value of $$g$$ at a height $$h$$ above the surface of the earth is the same as at a depth $$d$$ below the surface of earth. When both $$d$$ and $$h$$ are much smaller than the radius of earth, then which one of the following is correct?