JEE Main 2021 (Online) 25th July Morning Shift
Paper was held on
Sun, Jul 25, 2021 3:30 AM
Chemistry
1
Which one of the following species responds to an external magnetic field?
2
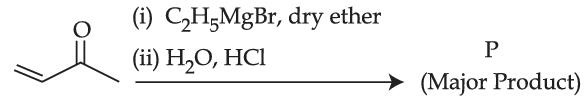
Consider the above reaction, the major product 'P' is :
3
The water soluble protein is :
4

Consider the given reaction, the product 'X' is :
5
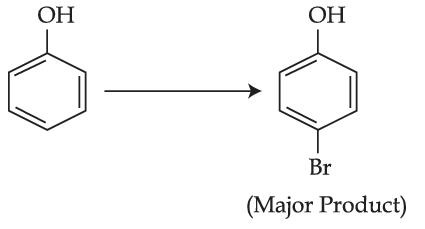
The given reaction can occur in the presence of :
(a) Bromine water
(b) Br2 in CS2, 273 K
(c) Br2/FeBr3
(d) Br2 in CHCl3, 273 K
Choose the correct answer from the options gien below :
6
Given below are two statements, one is labelled as Assertion (A) and other is labelled as Reason (R).
Assertion (A) : Gabriel phthalimide synthesis cannot be used to prepare aromatic primary amines.
Reason (R) : Aryl halides do not undergo nucleophilic substitution reaction.
In the light of the above statements, choose the correct answer from the options given below :
Assertion (A) : Gabriel phthalimide synthesis cannot be used to prepare aromatic primary amines.
Reason (R) : Aryl halides do not undergo nucleophilic substitution reaction.
In the light of the above statements, choose the correct answer from the options given below :
7
For the following graphs,
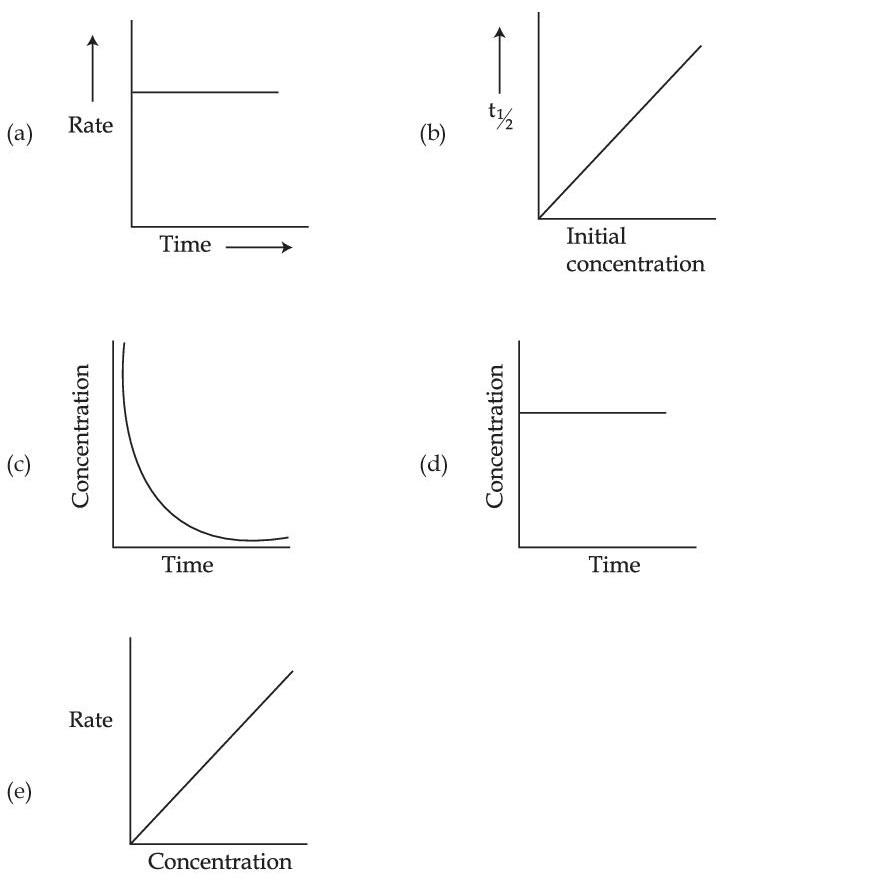
Choose from the options given below, the correct one regarding order of reaction is :

Choose from the options given below, the correct one regarding order of reaction is :
8
Which one of the products of the following reactions does not react with Hinsberg reagent to form sulphonamide?
9
The ionic radii of K+, Na+, Al3+ and Mg2+ are in the order:
10
Which one of the following compounds of Group-14 elements is not known?
11
Which one among the following resonating structures is not correct?
12
The correct order of following 3d metal oxides, according to their oxidation numbers is :
(a) CrO3, (b) Fe2O3, (c) MnO2, (d) V2O5, (e) Cu2O
(a) CrO3, (b) Fe2O3, (c) MnO2, (d) V2O5, (e) Cu2O
13
Which one of the following compounds will liberate CO2, when treated with NaHCO3 ?
14
An organic compound 'A' C4H8 on treatment with KMnO4/H+ yields compound 'B' C3H6O.
Compound 'A' also yields compound 'B' an ozonolysis. Compound 'A' is :
Compound 'A' also yields compound 'B' an ozonolysis. Compound 'A' is :
15
The number of sigma bonds in
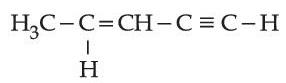
is _______________.
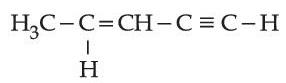
is _______________.
16
Three moles of AgCl get precipitated when one mole of an octahedral co-ordination compound with empirical formula CrCl3.3NH3.3H2O reacts with excess of silver nitrate. The number of chloride ions satisfying the secondary valency of the metal ion is ______________.
17
A source of monochromatic radiation of wavelength 400 nm provides 1000 J of energy in 10 seconds. When this radiation falls on the surface of sodium, x $$\times$$ 1020 electrons are ejected per second. Assume that wavelength 400 nm is sufficient for ejection of electron from the surface of sodium metal. The value of x is ______________. (Nearest integer)
(h = 6.626 $$\times$$ 10$$-$$34 Js)
(h = 6.626 $$\times$$ 10$$-$$34 Js)
18
CO2 gas is bubbled through water during a soft drink manufacturing process at 298 K. If CO2 exerts a partial pressure of 0.835 bar then x m mol of CO2 would dissolve in 0.9 L of water. The value of x is ____________. (Nearest integer)
(Henry's law constant for CO2 at 298 K is 1.67 $$\times$$ 103 bar)
(Henry's law constant for CO2 at 298 K is 1.67 $$\times$$ 103 bar)
19
For the reaction
A + B $$\rightleftharpoons$$ 2C
the value of equilibrium constant is 100 at 298 K. If the initial concentration of all the three species is 1 M each, then the equilibrium concentration of C is x $$\times$$ 10$$-$$1 M. The value of x is ____________. (Nearest integer)
A + B $$\rightleftharpoons$$ 2C
the value of equilibrium constant is 100 at 298 K. If the initial concentration of all the three species is 1 M each, then the equilibrium concentration of C is x $$\times$$ 10$$-$$1 M. The value of x is ____________. (Nearest integer)
20
Consider the cell at 25$$^\circ$$C
Zn | Zn2+ (aq), (1M) || Fe3+ (aq), Fe2+ (aq) | Pt(s)
The fraction of total iron present as Fe3+ ion at the cell potential of 1.500 V is x $$\times$$ 10$$-$$2. The value of x is ______________. (Nearest integer)
(Given : $$E_{F{e^{3 + }}/F{e^{2 + }}}^0 = 0.77V$$, $$E_{Z{n^{2 + }}/Zn}^0 = - 0.76V$$)
Zn | Zn2+ (aq), (1M) || Fe3+ (aq), Fe2+ (aq) | Pt(s)
The fraction of total iron present as Fe3+ ion at the cell potential of 1.500 V is x $$\times$$ 10$$-$$2. The value of x is ______________. (Nearest integer)
(Given : $$E_{F{e^{3 + }}/F{e^{2 + }}}^0 = 0.77V$$, $$E_{Z{n^{2 + }}/Zn}^0 = - 0.76V$$)
21
At 298 K, the enthalpy of fusion of a solid (X) is 2.8 kJ mol$$-$$1 and the enthalpy of vaporisation of the liquid (X) is 98.2 kJ mol$$-$$1. The enthalpy of sublimation of the substance (X) in kJ mol$$-$$1 is _____________. (in nearest integer)
22
When 10 mL of an aqueous solution of Fe2+ ions was titrated in the presence of dil H2SO4 using diphenylamine indicator, 15 mL of 0.02 M solution of K2Cr2O7 was required to get the end point. The molarity of the solution containing Fe2+ ions is x $$\times$$ 10$$-$$2 M. The value of x is __________. (Nearest integer)
23
Consider the complete combustion of butane, the amount of butane utilized to produce 72.0 g of water is ___________ $$\times$$ 10$$-$$1 g. (in nearest integer)
Mathematics
1
Let $$f(x) = 3{\sin ^4}x + 10{\sin ^3}x + 6{\sin ^2}x - 3$$, $$x \in \left[ { - {\pi \over 6},{\pi \over 2}} \right]$$. Then, f is :
2
Let Sn be the sum of the first n terms of an arithmetic progression. If S3n = 3S2n, then the value of $${{{S_{4n}}} \over {{S_{2n}}}}$$ is :
3
The locus of the centroid of the triangle formed by any point P on the hyperbola $$16{x^2} - 9{y^2} + 32x + 36y - 164 = 0$$, and its foci is :
4
Let f : R $$\to$$ R be defined as
$$f(x) = \left\{ {\matrix{ {{{\lambda \left| {{x^2} - 5x + 6} \right|} \over {\mu (5x - {x^2} - 6)}},} & {x < 2} \cr {{e^{{{\tan (x - 2)} \over {x - [x]}}}},} & {x > 2} \cr {\mu ,} & {x = 2} \cr } } \right.$$
where [x] is the greatest integer is than or equal to x. If f is continuous at x = 2, then $$\lambda$$ + $$\mu$$ is equal to :
$$f(x) = \left\{ {\matrix{ {{{\lambda \left| {{x^2} - 5x + 6} \right|} \over {\mu (5x - {x^2} - 6)}},} & {x < 2} \cr {{e^{{{\tan (x - 2)} \over {x - [x]}}}},} & {x > 2} \cr {\mu ,} & {x = 2} \cr } } \right.$$
where [x] is the greatest integer is than or equal to x. If f is continuous at x = 2, then $$\lambda$$ + $$\mu$$ is equal to :
5
The value of the definite integral $$\int\limits_{\pi /24}^{5\pi /24} {{{dx} \over {1 + \root 3 \of {\tan 2x} }}} $$ is :
6
If b is very small as compared to the value of a, so that the cube and other higher powers of $${b \over a}$$ can be neglected in the identity $${1 \over {a - b}} + {1 \over {a - 2b}} + {1 \over {a - 3b}} + ..... + {1 \over {a - nb}} = \alpha n + \beta {n^2} + \gamma {n^3}$$, then the value of $$\gamma$$ is :
7
Let y = y(x) be the solution of the differential equation $${{dy} \over {dx}} = 1 + x{e^{y - x}}, - \sqrt 2 < x < \sqrt 2 ,y(0) = 0$$
then, the minimum value of $$y(x),x \in \left( { - \sqrt 2 ,\sqrt 2 } \right)$$ is equal to :
then, the minimum value of $$y(x),x \in \left( { - \sqrt 2 ,\sqrt 2 } \right)$$ is equal to :
8
The area (in sq. units) of the region, given by the set $$\{ (x,y) \in R \times R|x \ge 0,2{x^2} \le y \le 4 - 2x\} $$ is :
9
Let g : N $$\to$$ N be defined as
g(3n + 1) = 3n + 2,
g(3n + 2) = 3n + 3,
g(3n + 3) = 3n + 1, for all n $$\ge$$ 0.
Then which of the following statements is true?
g(3n + 1) = 3n + 2,
g(3n + 2) = 3n + 3,
g(3n + 3) = 3n + 1, for all n $$\ge$$ 0.
Then which of the following statements is true?
10
Let $$f:[0,\infty ) \to [0,\infty )$$ be defined as $$f(x) = \int_0^x {[y]dy} $$
where [x] is the greatest integer less than or equal to x. Which of the following is true?
where [x] is the greatest integer less than or equal to x. Which of the following is true?
11
The values of a and b, for which the system of equations
2x + 3y + 6z = 8
x + 2y + az = 5
3x + 5y + 9z = b
has no solution, are :
2x + 3y + 6z = 8
x + 2y + az = 5
3x + 5y + 9z = b
has no solution, are :
12
Let 9 distinct balls be distributed among 4 boxes, B1, B2, B3 and B4. If the probability than B3 contains exactly 3 balls is $$k{\left( {{3 \over 4}} \right)^9}$$ then k lies in the set :
13
The number of real roots of the equation $${e^{6x}} - {e^{4x}} - 2{e^{3x}} - 12{e^{2x}} + {e^x} + 1 = 0$$ is :
14
Let an ellipse $$E:{{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1$$, $${a^2} > {b^2}$$, passes through $$\left( {\sqrt {{3 \over 2}} ,1} \right)$$ and has eccentricity $${1 \over {\sqrt 3 }}$$. If a circle, centered at focus F($$\alpha$$, 0), $$\alpha$$ > 0, of E and radius $${2 \over {\sqrt 3 }}$$, intersects E at two points P and Q, then PQ2 is equal to :
15
Let y = y(x) be solution of the following differential equation $${e^y}{{dy} \over {dx}} - 2{e^y}\sin x + \sin x{\cos ^2}x = 0,y\left( {{\pi \over 2}} \right) = 0$$ If $$y(0) = {\log _e}(\alpha + \beta {e^{ - 2}})$$, then $$4(\alpha + \beta )$$ is equal to ______________.
16
Consider the following frequency distribution :
If the sum of all frequencies is 584 and median is 45, then | $$\alpha$$ $$-$$ $$\beta$$ | is equal to _______________.
| Class : | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
|---|---|---|---|---|---|
| Frequency : | $$\alpha $$ | 110 | 54 | 30 | $$\beta $$ |
If the sum of all frequencies is 584 and median is 45, then | $$\alpha$$ $$-$$ $$\beta$$ | is equal to _______________.
17
Let $$\overrightarrow p = 2\widehat i + 3\widehat j + \widehat k$$ and $$\overrightarrow q = \widehat i + 2\widehat j + \widehat k$$ be two vectors. If a vector $$\overrightarrow r = (\alpha \widehat i + \beta \widehat j + \gamma \widehat k)$$ is perpendicular to each of the vectors ($$(\overrightarrow p + \overrightarrow q )$$ and $$(\overrightarrow p - \overrightarrow q )$$, and $$\left| {\overrightarrow r } \right| = \sqrt 3 $$, then $$\left| \alpha \right| + \left| \beta \right| + \left| \gamma \right|$$ is equal to _______________.
18
The ratio of the coefficient of the middle term in the expansion of (1 + x)20 and the sum of the coefficients of two middle terms in expansion of (1 + x)19 is _____________.
19
There are 5 students in class 10, 6 students in class 11 and 8 students in class 12. If the number of ways, in which 10 students can be selected from them so as to include at least 2 students from each class and at most 5 students from the total 11 students of class 10 and 11 is 100 k, then k is equal to _____________.
20
If $$\alpha$$, $$\beta$$ are roots of the equation $${x^2} + 5(\sqrt 2 )x + 10 = 0$$, $$\alpha$$ > $$\beta$$ and $${P_n} = {\alpha ^n} - {\beta ^n}$$ for each positive integer n, then the value of $$\left( {{{{P_{17}}{P_{20}} + 5\sqrt 2 {P_{17}}{P_{19}}} \over {{P_{18}}{P_{19}} + 5\sqrt 2 P_{18}^2}}} \right)$$ is equal to _________.
21
The term independent of 'x' in the expansion of
$${\left( {{{x + 1} \over {{x^{2/3}} - {x^{1/3}} + 1}} - {{x - 1} \over {x - {x^{1/2}}}}} \right)^{10}}$$, where x $$\ne$$ 0, 1 is equal to ______________.
$${\left( {{{x + 1} \over {{x^{2/3}} - {x^{1/3}} + 1}} - {{x - 1} \over {x - {x^{1/2}}}}} \right)^{10}}$$, where x $$\ne$$ 0, 1 is equal to ______________.
22
Let $$S = \left\{ {n \in N\left| {{{\left( {\matrix{
0 & i \cr
1 & 0 \cr
} } \right)}^n}\left( {\matrix{
a & b \cr
c & d \cr
} } \right) = \left( {\matrix{
a & b \cr
c & d \cr
} } \right)\forall a,b,c,d \in R} \right.} \right\}$$, where i = $$\sqrt { - 1} $$. Then the number of 2-digit numbers in the set S is _____________.
Physics
1
For a gas CP $$-$$ CV = R in a state P and CP $$-$$ CV = 1.10 R in a state Q, TP and TQ are the temperatures in two different states P and Q respectively. Then
2
Given below are two statements : one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A : Moment of inertia of a circular disc of mass 'M' and radius 'R' about X, Y axes (passing through its plane) and Z-axis which is perpendicular to its plane were found to be Ix, Iy and Iz respectively. The respectively radii of gyration about all the three axes will be the same.
Reason R : A rigid body making rotational motion has fixed mass and shape. In the light of the above statements, choose the most appropriate answer from the options given below :
Assertion A : Moment of inertia of a circular disc of mass 'M' and radius 'R' about X, Y axes (passing through its plane) and Z-axis which is perpendicular to its plane were found to be Ix, Iy and Iz respectively. The respectively radii of gyration about all the three axes will be the same.
Reason R : A rigid body making rotational motion has fixed mass and shape. In the light of the above statements, choose the most appropriate answer from the options given below :
3
What should be the order of arrangement of de-Broglie wavelength of electron ($$\lambda$$e), an $$\alpha$$-particle ($$\lambda$$a) and proton ($$\lambda$$p) given that all have the same kinetic energy?
4
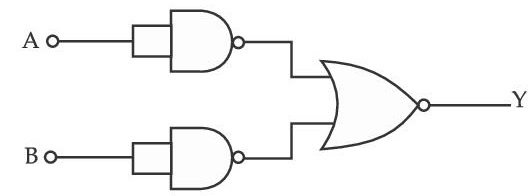
Identify the logic operation carried out.

5
A particle of mass 4M at rest disintegrates into two particles of mass M and 3M respectively having non zero velocities. The ratio of de-Broglie wavelength of particle of mass M to that of mass 3M will be :
6
Match List - I with List - II
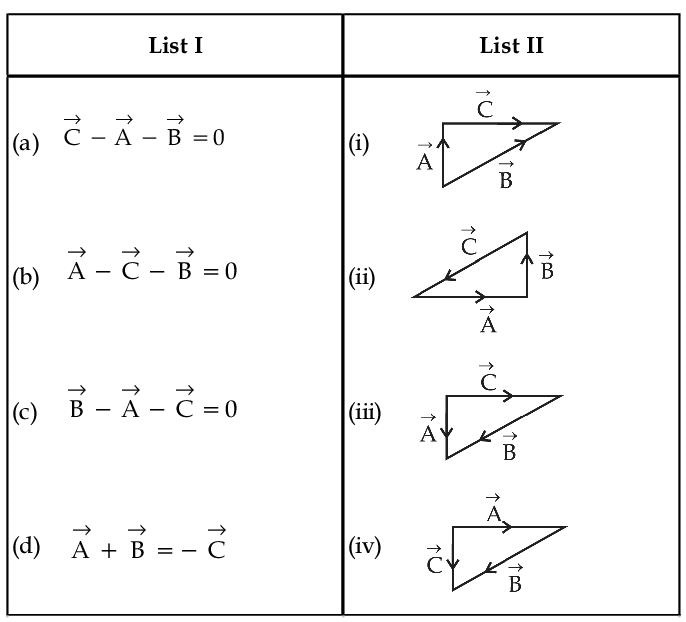
Choose the correct answer from the options given below :

Choose the correct answer from the options given below :
7
A parallel plate capacitor with plate area 'A' and distance of separation 'd' is filled with a dielectric. What is the capacity of the capacitor when permittivity of the dielectric varies as :
$$\varepsilon (x) = {\varepsilon _0} + kx$$, for $$\left( {0 < x \le {d \over 2}} \right)$$
$$\varepsilon (x) = {\varepsilon _0} + k(d - x)$$, for $$\left( {{d \over 2} \le x \le d} \right)$$
$$\varepsilon (x) = {\varepsilon _0} + kx$$, for $$\left( {0 < x \le {d \over 2}} \right)$$
$$\varepsilon (x) = {\varepsilon _0} + k(d - x)$$, for $$\left( {{d \over 2} \le x \le d} \right)$$
8
A monoatomic ideal gas, initially at temperature T1 is enclosed in a cylinder fitted with a frictionless piston. The gas is allowed to expand adiabatically to a temperature T2 by releasing the piston suddenly. If l1 and l2 are the lengths of the gas column, before and after the expansion respectively, then the value of $${{{T_1}} \over {{T_2}}}$$ will be :
9
A ray of laser of a wavelength 630 nm is incident at an angle of 30$$^\circ$$ at the diamond-air interface. It is going from diamond to air. The refractive index of diamond is 2.42 and that of air is 1. Choose the correct option.
10
Two wires of same length and radius are joined end to end and loaded. The Young's modulii of the materials of the two wires are Y1 and Y2. The combination behaves as a single wire then its Young's modulus is :
11
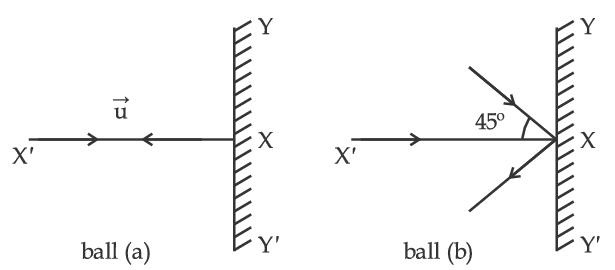
Two billiard balls of equal mass 30g strike a rigid wall with same speed of 108 kmph (as shown) but at different angles. If the balls get reflected with the same speed then the ratio of the magnitude of impulses imparted to ball 'a' and ball 'b' by the wall along 'X' direction is :

12
In the Young's double slit experiment, the distance between the slits varies in time as
d(t) = d0 + a0 sin$$\omega$$t; where d0, $$\omega$$ and a0 are constants. The difference between the largest fringe width and the smallest fringe width obtained over time is given as :
d(t) = d0 + a0 sin$$\omega$$t; where d0, $$\omega$$ and a0 are constants. The difference between the largest fringe width and the smallest fringe width obtained over time is given as :
13
Two different metal bodies A and B of equal mass are heated at a uniform rate under similar conditions. The variation of temperature of the bodies is graphically represented as shown in the figure. The ratio of specific heat capacities is :


14
A linearly polarized electromagnetic wave in vacuum is
$$E = 3.1\cos \left[ {(1.8)z - (5.4 \times {{10}^6})t} \right]\widehat iN/C$$
is incident normally on a perfectly reflecting wall at z = a. Choose the correct option
$$E = 3.1\cos \left[ {(1.8)z - (5.4 \times {{10}^6})t} \right]\widehat iN/C$$
is incident normally on a perfectly reflecting wall at z = a. Choose the correct option
15
Water droplets are coming from an open tap at a particular rate. The spacing between a droplet observed at 4th second after its fall to the next droplet is 34.3 m. At what rate the droplets are coming from the tap ? (Take g = 9.8 m/s2)
16
The minimum and maximum distances of a planet revolving around the sun are x1 and x2. If the minimum speed of the planet on its trajectory is v0 then its maximum speed will be :
17
A body of mass 2 kg moving with a speed of 4 m/s. makes an elastic collision with another body at rest and continues to move in the original direction but with one fourth of its initial peed. The speed of the two body centre of mass is $${x \over {10}}$$ m/s. Then the value of x is ___________.
18
Student A and student B used two screw gauges of equal pitch and 100 equal circular divisions to measure the radius of a given wire. The actual value of the radius of the wire is 0.322 cm. The absolute value of the difference between the final circular scale readings observed by the students A and B is ______________.
[Figure shows position of reference 'O' when jaws of screw gauge are closed]
Given pitch = 0.1 cm.
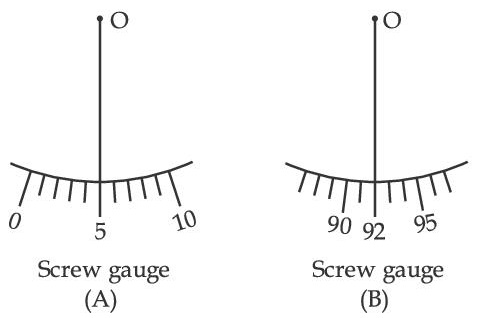
[Figure shows position of reference 'O' when jaws of screw gauge are closed]
Given pitch = 0.1 cm.

19
An inductor of 10 mH is connected to a 20V battery through a resistor of 10 k$$\Omega$$ and a switch. After a long time, when maximum current is set up in the circuit, the current is switched off. The current in the circuit after 1 $$\mu$$s is $${x \over {100}}$$ mA. Then x is equal to ___________. (Take e$$-$$1 = 0.37)
20
A circular conducting coil of radius 1 m is being heated by the change of magnetic field $$\overrightarrow B $$ passing perpendicular to the plane in which the coil is laid. The resistance of the coil is 2 $$\mu$$$$\Omega$$. The magnetic field is slowly switched off such that its magnitude changes in time as
$$B = {4 \over \pi } \times {10^{ - 3}}T\left( {1 - {t \over {100}}} \right)$$
The energy dissipated by the coil before the magnetic field is switched off completely is E = ___________ mJ.
$$B = {4 \over \pi } \times {10^{ - 3}}T\left( {1 - {t \over {100}}} \right)$$
The energy dissipated by the coil before the magnetic field is switched off completely is E = ___________ mJ.
21
In the reported figure, two bodies A and B of masses 200 g and 800 g are attached with the system of springs. Springs are kept in a stretched position with some extension when the system is released. The horizontal surface is assumed to be frictionless. The angular frequency will be ____________ rad/s when k = 20 N/m.


22
The value of aluminium susceptibility is 2.2 $$\times$$ 10$$-$$5. The percentage increase in the magnetic field if space within a current carrying toroid is filled with aluminium is $${x \over {{{10}^4}}}$$. Then the value of x is _________________.
23
A particle of mass 1 mg and charge q is lying at the mid-point of two stationary particles kept at a distance '2 m' when each is carrying same charge 'q'. If the free charged particle is displaced from its equilibrium position through distance 'x' (x < < 1 m). The particle executes SHM. Its angular frequency of oscillation will be ____________ $$\times$$ 105 rad/s if q2 = 10 C2.
24
An electric bulb rated as 200 W at 100 V is used in a circuit having 200 V supply. The resistance 'R' that must be put in series with the bulb so that the bulb delivers the same power is _____________ $$\Omega$$.
25
A pendulum bob has a speed of 3 m/s at its lowest position. The pendulum is 50 cm long. The speed of bob, when the length makes an angle of 60$$^\circ$$ to the vertical will be (g = 10 m/s2) ____________ m/s.
26
A particle of mass 'm' is moving in time 't' on a trajectory given by
$$\overrightarrow r = 10\alpha {t^2}\widehat i + 5\beta (t - 5)\widehat j$$
Where $$\alpha$$ and $$\beta$$ are dimensional constants.
The angular momentum of the particle becomes the same as it was for t = 0 at time t = ____________ seconds.
$$\overrightarrow r = 10\alpha {t^2}\widehat i + 5\beta (t - 5)\widehat j$$
Where $$\alpha$$ and $$\beta$$ are dimensional constants.
The angular momentum of the particle becomes the same as it was for t = 0 at time t = ____________ seconds.