The vapour pressure of acetone at 20^oC is 185 torr. When 1.2 g of a non-volatile substance was dissolved in 100 g of acetone at 20^oC, its vapour pressure was 183 torr. The molar mass (g mol^-1) of the substance is:

Which of the following compounds will exhibit geometrical isomerism?

In Carius method of estimation of halogens, 250 mg of an organic compound gave 141 mg of AgBr. The percentage of bromine in the compound is: (at. Mass Ag = 108; Br = 80)

The molecular formula of a commercial resin used for exchanging ions in water softening is C₈H₇SO₃Na (Mol. Wt. 206). What would be the maximum uptake of Ca²⁺ ions by the resin when expressed in mole per gram resin?

The following reaction is performed at 298 K
2NO(g) + O₂ (g) $$\leftrightharpoons$$ 2NO₂ (g)
The standard free energy of formation of NO(g) is 86.6 kJ/mol at 298 K. What is the standard free energy of formation of NO₂(g) at 298 K? (KP = 1.6 × 10¹²)

The standard Gibbs energy change at 300 K for the reaction 2A $$\leftrightharpoons$$ B + C is 2494.2 J. At a given time, the composition of the reaction mixture is [A] = 1/2, [B] = 2 and [C] = 1/2. The reaction proceeds in the: [R = 8.314 J/K/mol, e = 2.718]

Two Faraday of electricity is passed through a solution of CuSO₄. The mass of copper deposited at the cathode is: (at. mass of Cu = 63.5 amu)

The intermolecular interaction that is dependent on the inverse cube of distance between the molecule is:

Match the catalysts to the correct processes :

	Catalyst		Process
(A)	TiCl3	(i)	Wacker process
(B)	PdCl2	(ii)	Ziegler - Natta polymerization
(C)	CuCl2	(iii)	Contact process
(D)	V2O5	(iv)	Deacon's process

In the reaction


The product $$E$$ is :

Which compound would give $$5$$ - keto - $$2$$ - methylhexanal upon ozonolysis?

Which of the vitamins given below is water soluble?

In the following sequence of reactions:


The product C is

The synthesis of alkyl fluorides is best accomplished by:

The number of geometric isomers that can exist for square planar [Pt (Cl) (py) (NH₃) (NH₂OH)]+ is (py = pyridine) :

The colour of KMnO₄ is due to :

Which of the following compounds is not colored yellow?

Assertion : Nitrogen and Oxygen are the main components in the atmosphere but these do not react to form oxides of nitrogen.

Reason : The reaction between nitrogen and oxygen requires high temperature.

Which one has the highest boiling point?

Higher order (>3) reactions are rare due to

The ionic radii (in Å) of N^3–, O^2– and F^– are respectively:

Which of the following is the energy of a possible excited state of hydrogen?

If the function.

$$g\left( x \right) = \left\{ {\matrix{ {k\sqrt {x + 1} ,} & {0 \le x \le 3} \cr {m\,x + 2,} & {3 < x \le 5} \cr } } \right.$$

is differentiable, then the value of $$k+m$$ is :

The mean of the data set comprising of 16 observations is 16. If one of the observation valued 16 is deleted and three new observations valued 3, 4 and 5 are added to the data, then the mean of the resultant data, is :

$$\mathop {\lim }\limits_{x \to 0} {{\left( {1 - \cos 2x} \right)\left( {3 + \cos x} \right)} \over {x\tan 4x}}$$ is equal to

Let $$\alpha $$ and $$\beta $$ be the roots of equation $${x^2} - 6x - 2 = 0$$. If $${a_n} = {\alpha ^n} - {\beta ^n},$$ for $$n \ge 1,$$ then the value of $${{{a_{10}} - 2{a_8}} \over {2{a_9}}}$$ is equal to :

If $$12$$ different balls are to be placed in $$3$$ identical boxes, then the probability that one of the boxes contains exactly $$3$$ balls is :

Let $$y(x)$$ be the solution of the differential equation

$$\left( {x\,\log x} \right){{dy} \over {dx}} + y = 2x\,\log x,\left( {x \ge 1} \right).$$ Then $$y(e)$$ is equal to :

The area (in sq. units) of the region described by

$$\left\{ {\left( {x,y} \right):{y^2} \le 2x} \right.$$ and $$\left. {y \ge 4x - 1} \right\}$$ is :

The integral
$$\int\limits_2^4 {{{\log \,{x^2}} \over {\log {x^2} + \log \left( {36 - 12x + {x^2}} \right)}}dx} $$ is equal to :

The integral $$\int {{{dx} \over {{x^2}{{\left( {{x^4} + 1} \right)}^{3/4}}}}} $$ equals :

If $$A = \left[ {\matrix{ 1 & 2 & 2 \cr 2 & 1 & { - 2} \cr a & 2 & b \cr } } \right]$$ is a matrix satisfying the equation

$$A{A^T} = 9\text{I},$$ where $$I$$ is $$3 \times 3$$ identity matrix, then the ordered

pair $$(a, b)$$ is equal to :

The set of all values of $$\lambda $$ for which the system of linear equations:

$$\matrix{ {2{x_1} - 2{x_2} + {x_3} = \lambda {x_1}} \cr {2{x_1} - 3{x_2} + 2{x_3} = \lambda {x_2}} \cr { - {x_1} + 2{x_2} = \lambda {x_3}} \cr } $$

has a non-trivial solution

Let $$f(x)$$ be a polynomial of degree four having extreme values
at $$x=1$$ and $$x=2$$. If $$\mathop {\lim }\limits_{x \to 0} \left[ {1 + {{f\left( x \right)} \over {{x^2}}}} \right] = 3$$, then f$$(2)$$ is equal to :

Let $${\tan ^{ - 1}}y = {\tan ^{ - 1}}x + {\tan ^{ - 1}}\left( {{{2x} \over {1 - {x^2}}}} \right),$$
where $$\left| x \right| < {1 \over {\sqrt 3 }}.$$ Then a value of $$y$$ is :

Let $$O$$ be the vertex and $$Q$$ be any point on the parabola, $${{x^2} = 8y}$$. If the point $$P$$ divides the line segment $$OQ$$ internally in the ratio $$1:3$$, then locus of $$P$$ is :

Locus of the image of the point $$(2, 3)$$ in the line $$\left( {2x - 3y + 4} \right) + k\left( {x - 2y + 3} \right) = 0,\,k \in R,$$ is a :

The number of points, having both co-ordinates as integers, that lie in the interior of the triangle with vertices $$(0, 0)$$ $$(0, 41)$$ and $$(41, 0)$$ is :

If m is the A.M. of two distinct real numbers l and n $$(l,n > 1)$$ and $${G_1},{G_2}$$ and $${G_3}$$ are three geometric means between $$l$$ and n, then $$G_1^4\, + 2G_2^4\, + G_3^4$$ equals:

The number of integers greater than 6,000 that can be formed, using the digits 3, 5, 6, 7 and 8, without repetition, is:

A complex number z is said to be unimodular if $$\,\left| z \right| = 1$$. Suppose $${z_1}$$ and $${z_2}$$ are complex numbers such that $${{{z_1} - 2{z_2}} \over {2 - {z_1}\overline {{z_2}} }}$$ is unimodular and $${z_2}$$ is not unimodular. Then the point $${z_1}$$ lies on a :

Let A and B be two sets containing four and two elements respectively. Then, the number of subsets of the set A $\times$ B , each having atleast three elements are

As an electron makes a transition from an excited state to the ground state of a hydrogen - like atom/ion :

A red $$LED$$ emits light at $$0.1$$ watt uniformly around it. The amplitude of the electric field of the light at a distance of $$1$$ $$m$$ from the diode is :

Monochromatic light is incident on a glass prism of angle $$A$$. If the refractive index of the material of the prism is $$\mu $$, a ray, incident at an angle $$\theta $$. on the face $$AB$$ would get transmitted through the face $$AC$$ of the prism provided :

An inductor $$(L=0.03$$ $$H)$$ and a resistor $$\left( {R = 0.15\,k\Omega } \right)$$ are connected in series to a battery of $$15V$$ $$EMF$$ in a circuit shown below. The key $${K_1}$$ has been kept closed for a long time. Then at $$t=0$$, $${K_1}$$ is opened and key $${K_2}$$ is closed simultaneously. At $$t=1$$ $$ms,$$ the current in the circuit will be : $$\left( {{e^5} \cong 150} \right)$$

An $$LCR$$ circuit is equivalent to a damped pendulum. In an $$LCR$$ circuit the capacitor is charged to $${Q_0}$$ and then connected to the $$L$$ and $$R$$ as shown below :

If a student plots graphs of the square of maximum charge $$\left( {Q_{Max}^2} \right)$$ on the capacitor with time$$(t)$$ for two different values $${L_1}$$ and $${L_2}$$ $$\left( {{L_1} > {L_2}} \right)$$ of $$L$$ then which of the following represents this graph correctly ?
$$\left( {plots\,\,are\,\,schematic\,\,and\,\,niot\,\,drawn\,\,to\,\,scale} \right)$$

Assuming human pupil to have a radius of $$0.25$$ $$cm$$ and a comfortable viewing distance of $$25$$ $$cm$$, the minimum separation between two objects that human eye can resolve at $$500$$ $$nm$$ wavelength is :

On a hot summer night, the refractive index of air is smallest near the ground and increases with height from the ground. When a light beam is directed horizontally, the Huygens' principle leads us to conclude that as it travels, the light beam :

Two coaxial solenoids of different radius carry current $$I$$ in the same direction. $$\overrightarrow {{F_1}} $$ be the magnetic force on the inner solenoid due to the outer one and $$\overrightarrow {{F_2}} $$ be the magnetic force on the outer solenoid due to the inner one. Then :

A rectangular loop of sides $$10$$ $$cm$$ and $$5$$ $$cm$$ carrying a current $$1$$ of $$12A$$ is placed in different orientations as shown in the figures below :

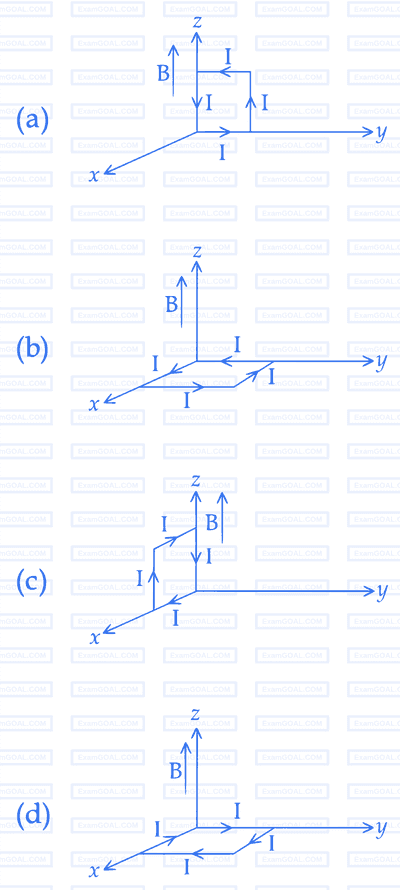
If there is a uniform magnetic field of $$0.3$$ $$T$$ in the positive $$z$$ direction, in which orientations the loop would be in $$(i)$$ stable equilibrium and $$(ii)$$ unstable equilibrium ?

Two stones are thrown up simultaneously from the edge of a cliff $$240$$ $$m$$ high with initial speed of $$10$$ $$m/s$$ and $$40$$ $$m/s$$ respectively. Which of the following graph best represents the time variation of relative position of the second stone with respect to the first ?

(Assume stones do not rebound after hitting the ground and neglect air resistance, take $$g = 10m/{s^2}$$)

(The figures are schematic and not drawn to scale)

In the circuit shown, the current in the $$1\Omega $$ resistor is :

Two long current carrying thin wires, both with current $$I,$$ are held by insulating threads of length $$L$$ and are in equilibrium as shown in the figure, with threads making an angle $$'\theta '$$ with the vertical. If wires have mass $$\lambda $$ per unit-length then the value of $$I$$ is :
($$g=$$ $$gravitational$$ $$acceleration$$ )

When $$5V$$ potential difference is applied across a wire of length $$0.1$$ $$m,$$ the drift speed of electrons is $$2.5 \times {10^{ - 4}}\,\,m{s^{ - 1}}.$$ If the electron density in the wire is $$8 \times {10^{28}}\,\,{m^{ - 3}},$$ the resistivity of the material is close to :

A long cylindrical shell carries positives surfaces change $$\sigma $$ in the upper half and negative surface charge - $$\sigma $$ in the lower half. The electric field lines around the cylinder will look like figure given in :
(figures are schematic and not drawn to scale)

A uniformly charged solid sphere of radius $$R$$ has potential $${V_0}$$ (measured with respect to $$\infty $$) on its surface. For this sphere the equipotential surfaces with potentials $${{3{V_0}} \over 2},\,{{5{V_0}} \over 4},\,{{3{V_0}} \over 4}$$ and $${{{V_0}} \over 4}$$ have radius $${R_1},\,\,{R_2},\,\,{R_3}$$ and $${R_4}$$ respectively. Then

In the given circuit, charges $${Q_2}$$ on the $$2\mu F$$ capacitor changes as $$C$$ is varied from $$1\,\mu F$$ to $$3\mu F.$$ $${Q_2}$$ as a function of $$'C'$$ is given properly by:
$$\left( {figures\,\,are\,\,drawn\,\,schematically\,\,and\,\,are\,\,not\,\,to\,\,scale} \right)$$

For a simple pendulum, a graph is plotted between its kinetic energy $$(KE)$$ and potential energy $$(PE)$$ against its displacement $$d.$$ Which one of the following represents these correctly?
$$(graphs$$ $$are$$ $$schematic$$ $$and$$ $$not$$ $$drawn$$ $$to$$ $$scale)$$

A pendulum made of a uniform wire of cross sectional area $$A$$ has time period $$T.$$ When an additional mass $$M$$ is added to its bob, the time period changes to $${T_{M.}}$$ If the Young's modulus of the material of the wire is $$Y$$ then $${1 \over Y}$$ is equal to :
($$g=$$ $$gravitational$$ $$acceleration$$)

From a solid sphere of mass $$M$$ and radius $$R,$$ a spherical portion of radius $$R/2$$ is removed, as shown in the figure. Taking gravitational potential $$V=0$$ at $$r = \infty ,$$ the potential at the center of the cavity thus formed is:
($$G=gravitational $$ $$constant$$)

Consider a spherical shell of radius $$R$$ at temperature $$T$$. The black body radiation inside it can be considered as an ideal gas of photons with internal energy per unit volume $$u = {U \over V}\, \propto \,{T^4}$$ and pressure $$p = {1 \over 3}\left( {{U \over V}} \right)$$ . If the shell now undergoes an adiabatic expansion the relation between $$T$$ and $$R$$ is:

Consider an ideal gas confined in an isolated closed chamber. As the gas undergoes an adiabatic expansion, the average time of collision between molecules increases as $${V^q},$$ where $$V$$ is the volume of the gas. The value of $$q$$ is: $$\left( {\gamma = {{{C_p}} \over {{C_v}}}} \right)$$

A solid body of constant heat capacity $$1$$ $$J/{}^ \circ C$$ is being heated by keeping it in contact with reservoirs in two ways:
$$(i)$$ Sequentially keeping in contact with $$2$$ reservoirs such that each reservoir
$$\,\,\,\,\,\,\,\,$$supplies same amount of heat.
$$(ii)$$ Sequentially keeping in contact with $$8$$ reservoirs such that each reservoir
$$\,\,\,\,\,\,\,\,\,\,$$supplies same amount of heat.
In both the cases body is brought from initial temperature $${100^ \circ }C$$ to final temperature $${200^ \circ }C$$. Entropy change of the body in the two cases respectively is :

Given in the figure are two blocks $$A$$ and $$B$$ of weight 20 N and 100 N, respectively. These are being pressed against a wall by a force $$F$$ as shown. If the coefficient of friction between the blocks is 0.1 and between block $$B$$ and the wall is 0.15, the frictional force applied by the wall on block $$B$$ is :

From a solid sphere of mass $$M$$ and radius $$R$$ a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its center and perpendicular to one of its face is:

Distance of the center of mass of a solid uniform cone from its vertex is $$z{}_0$$. If the radius of its base is $$R$$ and its height is $$h$$ then $$z{}_0$$ is equal to :

A particle of mass $$m$$ moving in the $$x$$ direction with speed $$2v$$ is hit by another particle of mass $$2m$$ moving in the $$y$$ direction with speed $$v.$$ If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to:

The period of oscillation of a simple pendulum is $$T = 2\pi \sqrt {{L \over g}} $$. Measured value of L is 20.0 cm known to 1 mm accuracy and time for 100 oscillations of the pendulum is found to be 90 s using wrist watch of 1 s resolution. The accuracy in the determination of g is: