JEE Main 2020 (Online) 3rd September Morning Slot
Paper was held on
Thu, Sep 3, 2020 3:30 AM
Chemistry
1
An acidic buffer is obtained on mixing :
2
The Kjeldahl method of Nitrogen estimation fails for which of the following reaction products?


3
Which one of the following compounds possesses the most acidic hydrogen?
4
The complex that can show optical activity is :
5
It is true that :
6
The atomic number of the element unnilennium is :
7
The photoelectric current from Na (Work function, w0
= 2.3 eV) is stopped by the output voltage of
the cell
Pt(s) | H2 (g, 1 Bar) | HCl (aq., pH =1) | AgCl(s) | Ag(s).
The pH of aq. HCl required to stop the photoelectric current form K(w0 = 2.25 eV), all other conditions remaining the same, is _______ $$ \times $$ 10-2 (to the nearest integer).
Given, 2.303$${{RT} \over F}$$ = 0.06 V;
$$E_{AgCl|Ag|C{l^ - }}^0$$ = 0.22 V
Pt(s) | H2 (g, 1 Bar) | HCl (aq., pH =1) | AgCl(s) | Ag(s).
The pH of aq. HCl required to stop the photoelectric current form K(w0 = 2.25 eV), all other conditions remaining the same, is _______ $$ \times $$ 10-2 (to the nearest integer).
Given, 2.303$${{RT} \over F}$$ = 0.06 V;
$$E_{AgCl|Ag|C{l^ - }}^0$$ = 0.22 V
8
The total number of monohalogenated organic
products in the following (including
stereoisomers) reaction is ______.


9
The volume strength of 8.9 M H2O2
solution calculated at 273 K and 1 atm is ______. (R = 0.0821 L
atm K-1 mol-1) (rounded off ot the nearest integer)
10
The mole fraction of glucose (C6H12O6
) in an aqueous binary solution is 0.1. The mass percentage of
water in it, to the nearest integer, is _______.
11
Let CNaCl
and CBaSO4 be the conductances (in S) measured for saturated aqueous solutions of NaCl
and BaSO4, respectively, at a temperature T.
Which of the following is false?
12
The mechanism of SN1 reaction is given as :

A student writes general characteristics based on the given mechanism as :
(a) The reaction is favoured by weak nucleophiles.
(b) R+ would be easily formed if the substituents are bulky.
(c) The reaction is accompanied by racemization.
(d) The reaction is favoured by non-polar solvents.

A student writes general characteristics based on the given mechanism as :
(a) The reaction is favoured by weak nucleophiles.
(b) R+ would be easily formed if the substituents are bulky.
(c) The reaction is accompanied by racemization.
(d) The reaction is favoured by non-polar solvents.
13
Henry’s constant (in kbar) for four gases $$\alpha $$, $$\beta $$, $$\gamma $$ and $$\delta $$ in water at 298 K is given below :
(density of water = 103 kg m-3 at 298 K)
This table implies that :
| $$\alpha $$ | $$\beta $$ | $$\gamma $$ | $$\delta $$ | |
|---|---|---|---|---|
| KH | 50 | 2 | 2 $$ \times $$ 10-5 | 0.5 |
(density of water = 103 kg m-3 at 298 K)
This table implies that :
14
The electronic spectrum of [Ti(H2O)6]3+ shows a single broad peak with a maximum at 20,300 cm-1
.
The crystal field stabilization energy (CFSE) of the complex ion, in kJ mol-1, is :
15
An organic compound [A], molecular formula C10H20O2
was hydrolyzed with dilute sulphuric acid to
give a carboxylic acid [B] and an alcohol [C]. Oxidation of [C] with
CrO3 - H2SO4 produced [B]. Which of the following strucutres are not possible for [A]?
CrO3 - H2SO4 produced [B]. Which of the following strucutres are not possible for [A]?
16
Glycerol is separated in soap industries by :
17
Of the species, NO, NO+, NO2+ and NO-
, the one with minimum bond strength is :
18
Which of the following compounds produces an optically inactive compound on hydrogenation?
Mathematics
1
For the frequency distribution :
Variate (x) : x1 x2 x3 .... x15
Frequency (f) : f1 f2 f3 ...... f15
where 0 < x1 < x2 < x3 < ... < x15 = 10 and
$$\sum\limits_{i = 1}^{15} {{f_i}} $$ > 0, the standard deviation cannot be :
Variate (x) : x1 x2 x3 .... x15
Frequency (f) : f1 f2 f3 ...... f15
where 0 < x1 < x2 < x3 < ... < x15 = 10 and
$$\sum\limits_{i = 1}^{15} {{f_i}} $$ > 0, the standard deviation cannot be :
2
2$$\pi $$ - $$\left( {{{\sin }^{ - 1}}{4 \over 5} + {{\sin }^{ - 1}}{5 \over {13}} + {{\sin }^{ - 1}}{{16} \over {65}}} \right)$$ is equal to :
3
Let [t] denote the greatest integer
$$ \le $$ t. If for some
$$\lambda $$ $$ \in $$ R - {1, 0}, $$\mathop {\lim }\limits_{x \to 0} \left| {{{1 - x + \left| x \right|} \over {\lambda - x + \left[ x \right]}}} \right|$$ = L, then L is equal to :
$$\lambda $$ $$ \in $$ R - {1, 0}, $$\mathop {\lim }\limits_{x \to 0} \left| {{{1 - x + \left| x \right|} \over {\lambda - x + \left[ x \right]}}} \right|$$ = L, then L is equal to :
4
The solution curve of the differential equation,
(1 + e-x)(1 + y2)$${{dy} \over {dx}}$$ = y2,
which passes through the point (0, 1), is :
(1 + e-x)(1 + y2)$${{dy} \over {dx}}$$ = y2,
which passes through the point (0, 1), is :
5
If $$\alpha $$ and $$\beta $$ are the roots of the equation
x2 + px + 2 = 0 and $${1 \over \alpha }$$ and $${1 \over \beta }$$ are the
roots of the equation 2x2 + 2qx + 1 = 0, then
$$\left( {\alpha - {1 \over \alpha }} \right)\left( {\beta - {1 \over \beta }} \right)\left( {\alpha + {1 \over \beta }} \right)\left( {\beta + {1 \over \alpha }} \right)$$ is equal to :
x2 + px + 2 = 0 and $${1 \over \alpha }$$ and $${1 \over \beta }$$ are the
roots of the equation 2x2 + 2qx + 1 = 0, then
$$\left( {\alpha - {1 \over \alpha }} \right)\left( {\beta - {1 \over \beta }} \right)\left( {\alpha + {1 \over \beta }} \right)\left( {\beta + {1 \over \alpha }} \right)$$ is equal to :
6
If the number of integral terms in the expansion
of (31/2 + 51/8)n is exactly 33, then the least value of n is :
of (31/2 + 51/8)n is exactly 33, then the least value of n is :
7
If $$\Delta $$ = $$\left| {\matrix{
{x - 2} & {2x - 3} & {3x - 4} \cr
{2x - 3} & {3x - 4} & {4x - 5} \cr
{3x - 5} & {5x - 8} & {10x - 17} \cr
} } \right|$$ =
Ax3 + Bx2 + Cx + D, then B + C is equal to :
Ax3 + Bx2 + Cx + D, then B + C is equal to :
8
The value of (2.1P0
– 3.2P1 + 4.3P2 .... up to
51th term)
+ (1! – 2! + 3! – ..... up to 51th term) is equal to :
+ (1! – 2! + 3! – ..... up to 51th term) is equal to :
9
The function, f(x) = (3x – 7)x2/3, x $$ \in $$ R, is
increasing for all x lying in :
10
If y2 + loge (cos2x) = y,
$$x \in \left( { - {\pi \over 2},{\pi \over 2}} \right)$$, then :
$$x \in \left( { - {\pi \over 2},{\pi \over 2}} \right)$$, then :
11
$$\int\limits_{ - \pi }^\pi {\left| {\pi - \left| x \right|} \right|dx} $$ is equal to :
12
Consider the two sets :
A = {m $$ \in $$ R : both the roots of
x2 – (m + 1)x + m + 4 = 0 are real}
and B = [–3, 5).
Which of the following is not true?
A = {m $$ \in $$ R : both the roots of
x2 – (m + 1)x + m + 4 = 0 are real}
and B = [–3, 5).
Which of the following is not true?
13
Let P be a point on the parabola, y2
= 12x and
N be the foot of the perpendicular drawn from
P on the axis of the parabola. A line is now
drawn through the mid-point M of PN, parallel
to its axis which meets the parabola at Q. If the
y-intercept of the line NQ is $${4 \over 3}$$,
then :
14
The area (in sq. units) of the region
{ (x, y) : 0 $$ \le $$ y $$ \le $$ x2 + 1, 0 $$ \le $$ y $$ \le $$ x + 1,
$${1 \over 2}$$ $$ \le $$ x $$ \le $$ 2 } is :
{ (x, y) : 0 $$ \le $$ y $$ \le $$ x2 + 1, 0 $$ \le $$ y $$ \le $$ x + 1,
$${1 \over 2}$$ $$ \le $$ x $$ \le $$ 2 } is :
15
A hyperbola having the transverse axis of
length
$$\sqrt 2 $$ has the same foci as that of the ellipse
3x2 + 4y2 = 12, then this hyperbola does not
pass through which of the following points?
16
If the first term of an A.P. is 3 and the sum of
its first 25 terms is equal to the sum of its next
15 terms, then the common difference of this
A.P. is :
17
The lines
$$\overrightarrow r = \left( {\widehat i - \widehat j} \right) + l\left( {2\widehat i + \widehat k} \right)$$ and
$$\overrightarrow r = \left( {2\widehat i - \widehat j} \right) + m\left( {\widehat i + \widehat j + \widehat k} \right)$$
$$\overrightarrow r = \left( {\widehat i - \widehat j} \right) + l\left( {2\widehat i + \widehat k} \right)$$ and
$$\overrightarrow r = \left( {2\widehat i - \widehat j} \right) + m\left( {\widehat i + \widehat j + \widehat k} \right)$$
18
A dice is thrown two times and the sum of the
scores appearing on the die is observed to be
a multiple of 4. Then the conditional probability
that the score 4 has appeared atleast once is :
19
If $${\left( {{{1 + i} \over {1 - i}}} \right)^{{m \over 2}}} = {\left( {{{1 + i} \over {1 - i}}} \right)^{{n \over 3}}} = 1$$, (m, n
$$ \in $$ N) then the
greatest common divisor of the least values of
m and n is _______ .
20
The diameter of the circle, whose centre lies on
the line x + y = 2 in the first quadrant and which
touches both the lines x = 3 and y = 2, is
_______ .
21
If $$\mathop {\lim }\limits_{x \to 0} \left\{ {{1 \over {{x^8}}}\left( {1 - \cos {{{x^2}} \over 2} - \cos {{{x^2}} \over 4} + \cos {{{x^2}} \over 2}\cos {{{x^2}} \over 4}} \right)} \right\}$$ = 2-k
then the value of k is _______ .
then the value of k is _______ .
22
The value of $${\left( {0.16} \right)^{{{\log }_{2.5}}\left( {{1 \over 3} + {1 \over {{3^2}}} + ....to\,\infty } \right)}}$$ is equal to ______.
23
Let A = $$\left[ {\matrix{
x & 1 \cr
1 & 0 \cr
} } \right]$$, x $$ \in $$ R and A4 = [aij].
If a11 = 109, then a22 is equal to _______ .
If a11 = 109, then a22 is equal to _______ .
Physics
1
Two isolated conducting spheres S1 and S2 of
radius $${2 \over 3}R$$ and $${1 \over 3}R$$ have 12 $$\mu $$C and –3 $$\mu $$C
charges, respectively, and are at a large
distance from each other. They are now
connected by a conducting wire. A long time
after this is done the charges on S1 and S2 are
respectively :
2
An observer can see through a small hole on the side of a jar (radius 15 cm) at a point at height of
15 cm from the bottom (see figure). The hole is at a height of 45 cm. When the jar is filled with a
liquid up to a height of 30 cm the same observer can see the edge at the bottom of the jar. If the
refractive index of the liquid is N/100, where N is an integer, the value of N is _____.


3
When a long glass capillary tube of radius
0.015 cm is dipped in a liquid, the liquid rises
to a height of 15 cm within it. If the contact angle
between the liquid and glass to close to 0o, the
surface tension of the liquid, in milliNewton m–1,
is [$$\rho $$(liquid) = 900 kgm–3, g = 10 ms–2]
(Give answer in closest integer) _____.
(Give answer in closest integer) _____.
4
A person of 80 kg mass is standing on the rim
of a circular platform of mass 200 kg rotating
about its axis at 5 revolutions per minute (rpm).
The person now starts moving towards the
centre of the platform. What will be the
rotational speed (in rpm) of the platform when
the person reaches its centre _________.
5
A cricket ball of mass 0.15 kg is thrown
vertically up by a bowling machine so that it
rises to a maximum height of 20 m after leaving
the machine. If the part pushing the ball applies
a constant force F on the ball and moves
horizontally a distance of 0.2 m while launching
the ball, the value of F (in N) is (g = 10 ms–2)
____.
6
A bakelite beaker has volume capacity of 500 cc at 30oC. When it is partially filled with Vm
volume
(at 30oC) of mercury, it is found that the unfilled volume of the beaker remains constant as
temperature is varied. If $$\gamma $$(beaker) = 6 × 10–6 oC–1 and $$\gamma $$(mercury) = 1.5 × 10–4 oC–1, where $$\gamma $$ is the
coefficient of volume expansion, then Vm
(in cc) is close to ____.
7
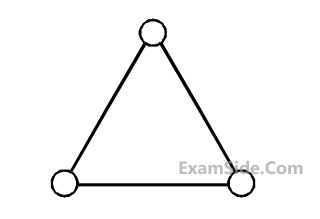 Consider a gas of triatomic molecules. The
molecules are assumed to be triangular and
made of massless rigid rods whose vertices
are occupied by atoms. The internal energy of
a mole of the gas at temperature T is :
Consider a gas of triatomic molecules. The
molecules are assumed to be triangular and
made of massless rigid rods whose vertices
are occupied by atoms. The internal energy of
a mole of the gas at temperature T is :8
Magnitude of magnetic field (in SI units) at the
centre of a hexagonal shape coil of side 10 cm,
50 turns and carrying current I (Ampere) in
units of $${{{\mu _0}I} \over \pi }$$ is :
9
In a Young’s double slit experiment, light of
500 nm is used to produce an interference
pattern. When the distance between the slits
is 0.05 mm, the angular width (in degree) of
the fringes formed on the distance screen is
close to
10
A block of mass m = 1 kg slides with velocity v = 6 m/s on a frictionless horizontal surface and
collides with a uniform vertical rod and sticks to it as shown. The rod is pivoted about O and swings
as a result of the collision making angle $$\theta $$ before momentarily coming to rest. If the rod has mass
M = 2 kg, and length $$l$$ = 1 m, the value of $$\theta $$ is approximately :
(take g = 10 m/s2)
(take g = 10 m/s2)

11
A uniform thin rope of length 12 m and mass 6 kg hangs vertically from a rigid support and a block
of mass 2 kg is attached to its free end. A transverse short wavetrain of wavelength 6 cm is
produced at the lower end of the rope. What is the wavelength of the wavetrain (in cm) when it
reaches the top of the rope ?
12
When a diode is forward biased, it has a
voltage drop of 0.5 V. The safe limit of current
through the diode is 10 mA. If a battery of emf
1.5 V is used in the circuit, the value of
minimum resistance to be connected in series
with the diode so that the current does not
exceed the safe limit is
13
An elliptical loop having resistance R, of semi major axis a, and semi minor axis b is placed in
magnetic field as shown in the figure. If the loop is rotated about the x-axis with angular frequency
$$\omega $$, the average power loss in the loop due to Joule heating is :


14
When the wavelength of radiation falling on a metal is changed from 500 nm to 200 nm, the
maximum kinetic energy of the photoelectrons becomes three times larger. The work function of
the metal is close to :
15
In the circuit shown in the figure, the total charge is 750 $$\mu $$C and the voltage across capacitor C2
is
20 V. Then the charge on capacitor C2
is :


16
A satellite is moving in a low nearly circular orbit around the earth. Its radius is roughly equal to
that of the earth’s radius Re
. By firing rockets attached to it, its speed is instantaneously increased
in the direction of its motion so that it become $$\sqrt {{3 \over 2}} $$
times larger. Due to this the farthest distance
from the centre of the earth that the satellite reaches is R. Value of R is :
17
A balloon filled with helium (32oC and 1.7 atm.)
bursts. Immediately afterwards the expansion
of helium can be considered as
18
Pressure inside two soap bubbles are 1.01 and 1.02 atmosphere, respectively. The ratio of their
volumes is :
19
A 750 Hz, 20 V (rms) source is connected to a
resistance of 100 $$\Omega $$, an inductance of 0.1803 H
and a capacitance of 10 $$\mu $$F all in series. The
time in which the resistance (heat capacity
2 J/oC) will get heated by 10oC. (assume no loss
of heat to the surroudnings) is close to :
20
A charged particle carrying charge 1 $$\mu $$C is moving
with velocity $$\left( {2\widehat i + 3\widehat j + 4\widehat k} \right)$$ ms–1. If an external
magnetic field of $$\left( {5\widehat i + 3\widehat j - 6\widehat k} \right)$$× 10–3 T exists in the region where the particle is moving then the
force on the particle is $$\overrightarrow F $$ × 10–9 N. The vector $$\overrightarrow F $$ is :
with velocity $$\left( {2\widehat i + 3\widehat j + 4\widehat k} \right)$$ ms–1. If an external
magnetic field of $$\left( {5\widehat i + 3\widehat j - 6\widehat k} \right)$$× 10–3 T exists in the region where the particle is moving then the
force on the particle is $$\overrightarrow F $$ × 10–9 N. The vector $$\overrightarrow F $$ is :
21
The magnetic field of a plane electromagnetic wave is
$$\overrightarrow B = 3 \times {10^{ - 8}}\sin \left[ {200\pi \left( {y + ct} \right)} \right]\widehat i$$ T
where c = 3 $$ \times $$ 108 ms–1 is the speed of light. The corresponding electric field is :
$$\overrightarrow B = 3 \times {10^{ - 8}}\sin \left[ {200\pi \left( {y + ct} \right)} \right]\widehat i$$ T
where c = 3 $$ \times $$ 108 ms–1 is the speed of light. The corresponding electric field is :
22
Moment of inertia of a cylinder of mass M,
length L and radius R about an axis passing
through its centre and perpendicular to the
axis of the cylinder is
I = $$M\left( {{{{R^2}} \over 4} + {{{L^2}} \over {12}}} \right)$$. If such a cylinder is to be made for a given mass of a material, the ratio $${L \over R}$$ for it to have minimum possible I is
I = $$M\left( {{{{R^2}} \over 4} + {{{L^2}} \over {12}}} \right)$$. If such a cylinder is to be made for a given mass of a material, the ratio $${L \over R}$$ for it to have minimum possible I is
23
Model a torch battery of length $$l$$ to be made up
of a thin cylindrical bar of radius ‘a’ and a
concentric thin cylindrical shell of radius ‘b’
filled in between with an electrolyte of
resistivity $$\rho $$ (see figure). If the battery is
connected to a resistance of value R, the
maximum Joule heating in R will take place for :
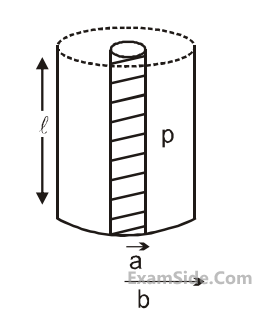

24
Using screw gauge of pitch 0.1 cm and
50 divisions on its circular scale, the thickness
of an object is measured. It should correctly be
recorded as