JEE Main 2020 (Online) 9th January Morning Slot
Paper was held on
Thu, Jan 9, 2020 3:30 AM
Chemistry
1
Identify (A) in the following reaction sequence :


2
If enthalpy of atomisation for Br2(1) is x kJ/mol
and bond enthalpy for Br2 is y kJ/mol, the
relation between them :
3
If the magnetic moment of a dioxygen species
is 1.73 B.M, it may be :
4
[Pd(F)(Cl)(Br)(I)]2– has n number of
geometrical isomers. Then, the spin-only
magnetic moment and crystal field stabilisation
energy [CFSE] of [Fe(CN)6]n–6, respectively,
are:
[Note : Ignore the pairing energy]
[Note : Ignore the pairing energy]
5
The Ksp for the following dissociation is
1.6 × 10–5
$$PbC{l_{2(s)}} \leftrightharpoons Pb_{(aq)}^{2 + } + 2Cl_{(aq)}^ - $$
Which of the following choices is correct for a mixture of 300 mL 0.134 M Pb(NO3)2 and 100 mL 0.4 M NaCl ?
$$PbC{l_{2(s)}} \leftrightharpoons Pb_{(aq)}^{2 + } + 2Cl_{(aq)}^ - $$
Which of the following choices is correct for a mixture of 300 mL 0.134 M Pb(NO3)2 and 100 mL 0.4 M NaCl ?
6
The correct order of heat of combustion for
following alkadienes is :






7
For the following reactions
$$A\buildrel {700K} \over \longrightarrow {\mathop{\rm Product}\nolimits} $$
$$A\mathrel{\mathop{\kern0pt\longrightarrow} \limits_{catalyst}^{500K}} {\mathop{\rm Product}\nolimits} $$
it was found that Ea is decreased by 30 kJ/mol in the presence of catalyst.
If the rate remains unchanged, the activation energy for catalysed reaction is (Assume pre exponential factor is same):
$$A\buildrel {700K} \over \longrightarrow {\mathop{\rm Product}\nolimits} $$
$$A\mathrel{\mathop{\kern0pt\longrightarrow} \limits_{catalyst}^{500K}} {\mathop{\rm Product}\nolimits} $$
it was found that Ea is decreased by 30 kJ/mol in the presence of catalyst.
If the rate remains unchanged, the activation energy for catalysed reaction is (Assume pre exponential factor is same):
8
The increasing order of basicity for the
following intermediates is (from weak to
strong)










9
The electronic configurations of bivalent
europium and trivalent cerium are
(atomic number : Xe = 54, Ce = 58, Eu = 63)
(atomic number : Xe = 54, Ce = 58, Eu = 63)
10
How much amount of NaCl should be added
to 600 g of water ($$\rho $$ = 1.00 g/mL) to decrease
the freezing point of water to – 0.2 °C ?
______.
(The freezing point depression constant for water = 2K kg mol–1)
(The freezing point depression constant for water = 2K kg mol–1)
11
The mass percentage of nitrogen in histamine is _____.
12
108 g of silver (molar mass 108 g mol–1) is
deposited at cathode from AgNO3(aq) solution
by a certain quantity of electricity. The
volume (in L) of oxygen gas produced at
273 K and 1 bar pressure from water by the
same quantity of electricity is _______.
13
The molarity of HNO3 in a sample which has
density 1.4 g/mL and mass percentage of 63%
is _____.
(Molecular Weight of HNO3 = 63)
(Molecular Weight of HNO3 = 63)
14
The hardness of a water sample containing
10–3 M MgSO4 expressed as CaCO3 equivalents
(in ppm) is ______.
(molar mass of MgSO4 is 120.37 g/mol)
(molar mass of MgSO4 is 120.37 g/mol)
15
The de Broglie wavelength of an electron in the
4th Bohr orbit is :
16
The major product (Y) in the following
reactions is :


17
Complex X of composition Cr(H2O)6Cln
has a spin only magnetic moment of 3.83
BM. It reacts with AgNO3 and shows
geometrical isomerism. The IUPAC
nomenclature of X is :
18
The compound that cannot act both as oxidising
and reducing agent is :
19
Which of these will produce the highest yield
in Friedel Crafts reaction?
20
The major product Z obtained in the following
reaction scheme is :


21
The acidic, basic and amphoteric oxides,
respectively, are :
22
B has a smaller first ionization enthalpy than
Be. Consider the following statements :
(I) It is easier to remove 2p electron than 2s electron
(II) 2p electron of B is more shielded from the nucleus by the inner core of electrons than the 2s electrons of Be.
(III) 2s electron has more penetration power than 2p electron.
(IV) atomic radius of B is more than Be (Atomic number B = 5, Be = 4)
The correct statements are :
(I) It is easier to remove 2p electron than 2s electron
(II) 2p electron of B is more shielded from the nucleus by the inner core of electrons than the 2s electrons of Be.
(III) 2s electron has more penetration power than 2p electron.
(IV) atomic radius of B is more than Be (Atomic number B = 5, Be = 4)
The correct statements are :
Mathematics
1
If ƒ'(x) = tan–1(secx + tanx), $$ - {\pi \over 2} < x < {\pi \over 2}$$,
and ƒ(0) = 0, then ƒ(1) is equal to :
and ƒ(0) = 0, then ƒ(1) is equal to :
2
The value of
$$\int\limits_0^{2\pi } {{{x{{\sin }^8}x} \over {{{\sin }^8}x + {{\cos }^8}x}}} dx$$ is equal to :
$$\int\limits_0^{2\pi } {{{x{{\sin }^8}x} \over {{{\sin }^8}x + {{\cos }^8}x}}} dx$$ is equal to :
3
In a box, there are 20 cards, out of which 10
are lebelled as A and the remaining 10 are
labelled as B. Cards are drawn at random, one
after the other and with replacement, till a
second A-card is obtained. The probability that
the second A-card appears before the third
B-card is :
4
Let z be complex number such that
$$\left| {{{z - i} \over {z + 2i}}} \right| = 1$$ and |z| = $${5 \over 2}$$.
Then the value of |z + 3i| is :
$$\left| {{{z - i} \over {z + 2i}}} \right| = 1$$ and |z| = $${5 \over 2}$$.
Then the value of |z + 3i| is :
5
A spherical iron ball of 10 cm radius is
coated with a layer of ice of uniform
thickness the melts at a rate of 50 cm3/min.
When the thickness of ice is 5 cm, then the rate
(in cm/min.) at which of the thickness of ice
decreases, is :
6
If the number of five digit numbers with distinct
digits and 2 at the 10th place is 336 k, then k
is equal to :
7
Let ƒ be any function continuous on [a, b] and
twice differentiable on (a, b). If for all x $$ \in $$ (a, b),
ƒ'(x) > 0 and ƒ''(x) < 0, then for any c $$ \in $$ (a, b),
$${{f(c) - f(a)} \over {f(b) - f(c)}}$$ is greater than :
8
The projection of the line segment joining the
points (1, –1, 3) and (2, –4, 11) on the line
joining the points (–1, 2, 3) and (3, –2, 10)
is ____________.
9
If for x $$ \ge $$ 0, y = y(x) is the solution of the
differential equation
(x + 1)dy = ((x + 1)2 + y – 3)dx, y(2) = 0, then y(3) is equal to _______.
(x + 1)dy = ((x + 1)2 + y – 3)dx, y(2) = 0, then y(3) is equal to _______.
10
The coefficient of x4 is the expansion of
(1 + x + x2)10 is _____.
11
If for some $$\alpha $$ and $$\beta $$ in R, the intersection of the
following three places
x + 4y – 2z = 1
x + 7y – 5z = b
x + 5y + $$\alpha $$z = 5
is a line in R3, then $$\alpha $$ + $$\beta $$ is equal to :
x + 4y – 2z = 1
x + 7y – 5z = b
x + 5y + $$\alpha $$z = 5
is a line in R3, then $$\alpha $$ + $$\beta $$ is equal to :
12
The number of distinct solutions of the equation
$${\log _{{1 \over 2}}}\left| {\sin x} \right| = 2 - {\log _{{1 \over 2}}}\left| {\cos x} \right|$$ in the interval [0, 2$$\pi $$], is ____.
$${\log _{{1 \over 2}}}\left| {\sin x} \right| = 2 - {\log _{{1 \over 2}}}\left| {\cos x} \right|$$ in the interval [0, 2$$\pi $$], is ____.
13
The integral $$\int {{{dx} \over {{{(x + 4)}^{{8 \over 7}}}{{(x - 3)}^{{6 \over 7}}}}}} $$ is equal to :
(where C is a constant of integration)
(where C is a constant of integration)
14
If $$f(x) = \left\{ {\matrix{
{{{\sin (a + 2)x + \sin x} \over x};} & {x < 0} \cr
{b\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;} & {x = 0} \cr
{{{{{\left( {x + 3{x^2}} \right)}^{{1 \over 3}}} - {x^{ {1 \over 3}}}} \over {{x^{{4 \over 3}}}}};} & {x > 0} \cr
} } \right.$$
is continuous at x = 0, then a + 2b is equal to :
is continuous at x = 0, then a + 2b is equal to :
15
Let C be the centroid of the triangle with
vertices (3, –1), (1, 3) and (2, 4). Let P be the
point of intersection of the lines x + 3y – 1 = 0
and 3x – y + 1 = 0. Then the line passing through
the points C and P also passes through the
point :
16
The value of
$${\cos ^3}\left( {{\pi \over 8}} \right)$$$${\cos}\left( {{3\pi \over 8}} \right)$$+$${\sin ^3}\left( {{\pi \over 8}} \right)$$$${\sin}\left( {{3\pi \over 8}} \right)$$
is :
$${\cos ^3}\left( {{\pi \over 8}} \right)$$$${\cos}\left( {{3\pi \over 8}} \right)$$+$${\sin ^3}\left( {{\pi \over 8}} \right)$$$${\sin}\left( {{3\pi \over 8}} \right)$$
is :
17
If for all real triplets (a, b, c), ƒ(x) = a + bx + cx2;
then $$\int\limits_0^1 {f(x)dx} $$ is equal to :
18
If e1 and e2 are the eccentricities of the ellipse,
$${{{x^2}} \over {18}} + {{{y^2}} \over 4} = 1$$ and the hyperbola, $${{{x^2}} \over 9} - {{{y^2}} \over 4} = 1$$ respectively and (e1, e2) is a point on the ellipse,
15x2 + 3y2 = k, then k is equal to :
19
Let the observations xi (1 $$ \le $$ i $$ \le $$ 10) satisfy the
equations, $$\sum\limits_{i = 1}^{10} {\left( {{x_1} - 5} \right)} $$ = 10 and $$\sum\limits_{i = 1}^{10} {{{\left( {{x_1} - 5} \right)}^2}} $$ = 40.
If $$\mu $$ and $$\lambda $$ are the mean and the variance of the
observations, x1 – 3, x2 – 3, ...., x10 – 3, then
the ordered pair ($$\mu $$, $$\lambda $$) is equal to :
equations, $$\sum\limits_{i = 1}^{10} {\left( {{x_1} - 5} \right)} $$ = 10 and $$\sum\limits_{i = 1}^{10} {{{\left( {{x_1} - 5} \right)}^2}} $$ = 40.
If $$\mu $$ and $$\lambda $$ are the mean and the variance of the
observations, x1 – 3, x2 – 3, ...., x10 – 3, then
the ordered pair ($$\mu $$, $$\lambda $$) is equal to :
20
The number of real roots of the equation,
e4x + e3x – 4e2x + ex + 1 = 0 is :
e4x + e3x – 4e2x + ex + 1 = 0 is :
Physics
1
In a fluorescent lamp choke (a small
transformer) 100 V of reverse voltage is
produced when the choke current changes
uniformly from 0.25 A to 0 in a duration of
0.025 ms. The self-inductance of the choke
(in mH) is estimated to be ________.
2
Both the diodes used in the circuit shown are
assumed to be ideal and have negligible
resistance when these are forward biased. Built
in potential in each diode is 0.7 V. For the input
voltages shown in the figure, the voltage
(in Volts) at point A is __________.


3
A body of mass m = 10 kg is attached to one
end of a wire of length 0.3 m. The maximum
angular speed (in rad s–1) with which it can be
rotated about its other end in space station is :
(Breaking stress of wire = 4.8 × 107 Nm–2 and
area of cross-section of the wire = 10–2 cm2) is:
(Breaking stress of wire = 4.8 × 107 Nm–2 and
area of cross-section of the wire = 10–2 cm2) is:
4
The distance x covered by a particle in one
dimensional motion varies with time t as
x2 = at2 + 2bt + c. If the acceleration of the particle depends on x as x–n, where n is an integer, the value of n is __________
x2 = at2 + 2bt + c. If the acceleration of the particle depends on x as x–n, where n is an integer, the value of n is __________
5
One end of a straight uniform 1m long bar is
pivoted on horizontal table. It is released from
rest when it makes an angle 30º from the
horizontal (see figure). Its angular speed when
it hits the table is given as $$\sqrt n $$ s-1, where n is
an integer. The value of n is _________.
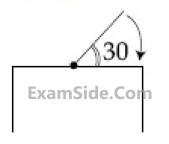

6
Water flows in a horizontal tube (see figure).
The pressure of water changes by 700 Nm–2
between A and B where the area of cross section
are 40 cm2 and 20 cm2, respectively. Find the
rate of flow of water through the tube.
(density of water = 1000 kgm–3)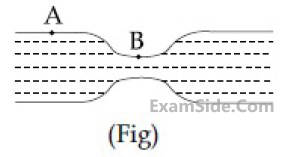
The pressure of water changes by 700 Nm–2
between A and B where the area of cross section
are 40 cm2 and 20 cm2, respectively. Find the
rate of flow of water through the tube.
(density of water = 1000 kgm–3)

7
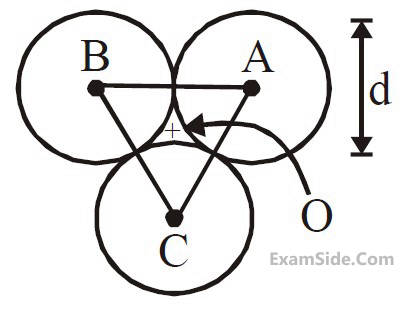 Three solid spheres each of mass m and
diameter d are stuck together such that the lines
connecting the centres form an equilateral
triangle of side of length d. The ratio I0/IA of
moment of inertia I0 of the system about an axis
passing the centroid and about center of any
of the spheres IA and perpendicular to the plane
of the triangle is :
Three solid spheres each of mass m and
diameter d are stuck together such that the lines
connecting the centres form an equilateral
triangle of side of length d. The ratio I0/IA of
moment of inertia I0 of the system about an axis
passing the centroid and about center of any
of the spheres IA and perpendicular to the plane
of the triangle is :8
An electric dipole of moment
$$\overrightarrow p = \left( { - \widehat i - 3\widehat j + 2\widehat k} \right) \times {10^{ - 29}} $$ C.m is
at the origin (0, 0, 0). The electric field due to this dipole at
$$\overrightarrow r = + \widehat i + 3\widehat j + 5\widehat k$$ (note that $$\overrightarrow r .\overrightarrow p = 0$$ ) is parallel to :
$$\overrightarrow p = \left( { - \widehat i - 3\widehat j + 2\widehat k} \right) \times {10^{ - 29}} $$ C.m is
at the origin (0, 0, 0). The electric field due to this dipole at
$$\overrightarrow r = + \widehat i + 3\widehat j + 5\widehat k$$ (note that $$\overrightarrow r .\overrightarrow p = 0$$ ) is parallel to :
9
Three harmonic waves having equal frequency
$$\nu $$ and same intensity $${I_0}$$, have phase angles 0, $${\pi \over 4}$$ and $$ - {\pi \over 4}$$ respectively. When they are
superimposed the intensity of the resultant wave
is close to :
10
A charged particle of mass 'm' and charge 'q'
moving under the influence of uniform electric
field $$E\overrightarrow i $$
and a uniform magnetic field $$B\overrightarrow k $$
follows a trajectory from point P to Q as shown
in figure. The velocities at P and Q are
respectively, $$v\overrightarrow i $$ and $$ - 2v\overrightarrow j $$
. Then which of the
following statements (A, B, C, D) are the
correct ?
(Trajectory shown is schematic and not to scale) :
(A) E = $${3 \over 4}\left( {{{m{v^2}} \over {qa}}} \right)$$
(B) Rate of work done by the electric field at P is $${3 \over 4}\left( {{{m{v^3}} \over a}} \right)$$
(C) Rate of work done by both the fields at Q is zero
(D) The difference between the magnitude of angular momentum of the particle at P and Q is 2mav.
(Trajectory shown is schematic and not to scale) :

(A) E = $${3 \over 4}\left( {{{m{v^2}} \over {qa}}} \right)$$
(B) Rate of work done by the electric field at P is $${3 \over 4}\left( {{{m{v^3}} \over a}} \right)$$
(C) Rate of work done by both the fields at Q is zero
(D) The difference between the magnitude of angular momentum of the particle at P and Q is 2mav.
11
Which of the following is an equivalent cyclic
process corresponding to the thermodynamic cyclic
given in the figure ? where, 1 $$ \to $$ 2 is adiabatic.
(Graphs are schematic and are not to scale)
(Graphs are schematic and are not to scale)

12
In the given circuit diagram, a wire is joining
points B and D. The current in this wire is :


13
Two particles of equal mass m have respective
initial velocities $$u\widehat i$$ and $$u\left( {{{\widehat i + \widehat j} \over 2}} \right)$$.
They collide completely inelastically. The energy lost in the process is :
initial velocities $$u\widehat i$$ and $$u\left( {{{\widehat i + \widehat j} \over 2}} \right)$$.
They collide completely inelastically. The energy lost in the process is :
14
If the screw on a screw-gauge is given six
rotations, it moves by 3 mm on the main scale.
If there are 50 divisions on the circular scale
the least count of the screw gauge is :
15
Consider two ideal diatomic gases A and B at
some temperature T. Molecules of the gas A are
rigid, and have a mass m. Molecules of the gas
B have an additional vibrational mode, and
have a mass $${m \over 4}$$
. The ratio of the specific heats ($$C_V^A$$ and $$C_V^B$$ ) of gas A and B, respectively is :
16
A particle moving with kinetic energy E has
de Broglie wavelength $$\lambda $$. If energy $$\Delta $$E is added
to its energy, the wavelength become $$\lambda $$/2. Value
of $$\Delta $$E, is :
17
Consider a force $$\overrightarrow F = - x\widehat i + y\widehat j$$
. The work done
by this force in moving a particle from point
A(1, 0) to B(0, 1) along the line segment is :
(all quantities are in SI units)
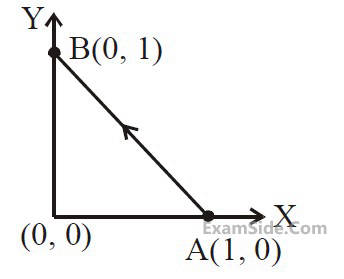

18
A body A of mass m is moving in a circular orbit
of radius R about a planet. Another body B of
mass
$${m \over 2}$$
collides with A with a velocity which is half $$\left( {{{\overrightarrow v } \over 2}} \right)$$ the instantaneous velocity$${\overrightarrow v }$$
of A.
The collision is completely inelastic. Then, the
combined body :
19
Consider a sphere of radius R which carries a
uniform charge density $$\rho $$. If a sphere of radius $${{R \over 2}}$$ is carved out of it, as shown, the ratio $${{\left| {\overrightarrow {{E_A}} } \right|} \over {\left| {\overrightarrow {{E_B}} } \right|}}$$ of magnitude of electric field $${\overrightarrow {{E_A}} }$$ and $${\overrightarrow {{E_B}} }$$,
respectively, at points A and B due to the
remaining portion is :


20
The electric fields of two plane electromagnetic
plane waves in vacuum are given by
$$\overrightarrow {{E_1}} = {E_0}\widehat j\cos \left( {\omega t - kx} \right)$$ and
$$\overrightarrow {{E_2}} = {E_0}\widehat k\cos \left( {\omega t - ky} \right)$$
At t = 0, a particle of charge q is at origin with
a velocity $$\overrightarrow v = 0.8c\widehat j$$ (c is the speed of light in vacuum). The instantaneous force experienced by the particle is :
$$\overrightarrow {{E_1}} = {E_0}\widehat j\cos \left( {\omega t - kx} \right)$$ and
$$\overrightarrow {{E_2}} = {E_0}\widehat k\cos \left( {\omega t - ky} \right)$$
At t = 0, a particle of charge q is at origin with
a velocity $$\overrightarrow v = 0.8c\widehat j$$ (c is the speed of light in vacuum). The instantaneous force experienced by the particle is :
21
A long, straight wire of radius a carries a current
distributed uniformly over its cross-section. The
ratio of the magnetic fields due to the wire at
distance
$${a \over 3}$$
and 2$$a$$, respectively from the axis
of the wire is :
22
Radiation, with wavelength 6561 $$\mathop A\limits^o $$ falls on a
metal surface to produce photoelectrons. The
electrons are made to enter a uniform magnetic
field of 3 × 10–4 T. If the radius of the largest
circular path followed by the electrons is
10 mm, the work function of the metal is
close to :
23
The aperture diameter of a telescope is 5m. The
separation between the moon and the earth is
4 × 105 km. With light of wavelength of
5500 $$\mathop A\limits^o $$, the minimum separation between
objects on the surface of moon, so that they are
just resolved, is close to :
24
A vessel of depth 2h is half filled with a liquid
of refractive index $$2\sqrt 2 $$ and the upper half with
another liquid of refractive index $$\sqrt 2 $$ . The
liquids are immiscible. The apparent depth of
the inner surface of the bottom of vessel
will be :
25
A quantity f is given by $$f = \sqrt {{{h{c^5}} \over G}} $$ where c is
speed of light, G universal gravitational
constant and h is the Planck's constant.
Dimension of f is that of :