JEE Main 2023 (Online) 30th January Evening Shift
Paper was held on
Mon, Jan 30, 2023 9:30 AM
Chemistry
1
Formulae for Nessler's reagent is :
2
Given below are two statements: One is labelled as Assertion A and the other is labelled as Reason R.
Assertion A:
can be easily reduced using $\mathrm{Zn}-\mathrm{Hg} / \mathrm{HCl}$ to 
Reason $\mathrm{R}: \mathrm{Zn}-\mathrm{Hg} / \mathrm{HCl}$ is used to reduce carbonyl group to $-\mathrm{CH}_{2}-$ group.
In the light of the above statements, choose the correct answer from the options given below:
Assertion A:
can be easily reduced using $\mathrm{Zn}-\mathrm{Hg} / \mathrm{HCl}$ to Reason $\mathrm{R}: \mathrm{Zn}-\mathrm{Hg} / \mathrm{HCl}$ is used to reduce carbonyl group to $-\mathrm{CH}_{2}-$ group.
In the light of the above statements, choose the correct answer from the options given below:
3
The most stable carbocation for the following is:
4
Match List I with List II:
| List I (Complexes) | List II (Hybridisation) | ||
|---|---|---|---|
| A. | $\left[\mathrm{Ni}(\mathrm{CO})_{4}\right]$ | I. | $\mathrm{sp}^{3}$ |
| B. | $\left[\mathrm{Cu}\left(\mathrm{NH}_{3}\right)_{4}\right]^{2+}$ | II. | dsp$^{2}$ |
| C. | $\left[\mathrm{Fe}\left(\mathrm{NH}_{3}\right)_{6}\right]^{2+}$ | III. | $\mathrm{sp}^{3}\mathrm{d}^{2}$ |
| D. | $\left[\mathrm{Fe}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{2+}$ | IV. | $\mathrm{d}^{2} \mathrm{sp}^{3}$ |
5
The $\mathrm{Cl}-\mathrm{Co}-\mathrm{Cl}$ bond angle values in a fac- $\left[\mathrm{Co}\left(\mathrm{NH}_{3}\right)_{3} \mathrm{Cl}_{3}\right]$ complex is/are :
6
Decreasing order towards SN 1 reaction for the following compounds is:
7
$\mathrm{KMnO}_4$ oxidises $\mathrm{I}^{-}$ in acidic and neutral/faintly alkaline solutions, respectively, to :
8
In the above conversion of compound $(\mathrm{X})$ to product $(\mathrm{Y})$, the sequence of reagents to be used will be:
9
Match List I with List II:
| List I (Mixture) | List II (Separation Technique) | ||
|---|---|---|---|
| A. | $\mathrm{CHCl}_3+\mathrm{C}_6 \mathrm{H}_5 \mathrm{NH}_2$ | I. | Steam distillation |
| B. | $\mathrm{C}_6 \mathrm{H}_{14}+\mathrm{C}_5 \mathrm{H}_{12}$ | II. | Differential extraction |
| C. | $\mathrm{C}_6 \mathrm{H}_5 \mathrm{NH}_2+\mathrm{H}_2 \mathrm{O}$ | III. | Distillation |
| D. | $\text { Organic compound in } \mathrm{H}_2 \mathrm{O}$ | IV. | Fractional distillation |
10
Maximum number of electrons that can be accommodated in shell with $n=4$ are:
11
Bond dissociation energy of "E-H" bond of the "$\mathrm{H}_{2} \mathrm{E}$ " hydrides of group 16 elements (given below), follows order.
A. $\mathrm{O}$
B. $\mathrm{S}$
C. Se
D. $\mathrm{Te}$
Choose the correct from the options given below:
A. $\mathrm{O}$
B. $\mathrm{S}$
C. Se
D. $\mathrm{Te}$
Choose the correct from the options given below:
12
The correct order of $\mathrm{pK}_{\mathrm{a}}$ values for the following compounds is:
13
$1 \mathrm{~L}, 0.02 \mathrm{M}$ solution of $\left[\mathrm{Co}\left(\mathrm{NH}_{3}\right)_{5} \mathrm{SO}_{4}\right]$ Br is mixed with $1 \mathrm{~L}, 0.02 \mathrm{M}$ solution of $\left[\mathrm{Co}\left(\mathrm{NH}_{3}\right)_{5} \mathrm{Br}\right] \mathrm{SO}_{4}$. The resulting solution is divided into two equal parts $(\mathrm{X})$ and treated with excess of $\mathrm{AgNO}_{3}$ solution and $\mathrm{BaCl}_{2}$ solution respectively as shown below:
$1 \mathrm{~L}$ Solution $(\mathrm{X})+\mathrm{AgNO}_{3}$ solution (excess) $\longrightarrow \mathrm{Y}$
$1 \mathrm{~L}$ Solution $(\mathrm{X})+\mathrm{BaCl}_{2}$ solution (excess) $\longrightarrow \mathrm{Z}$
The number of moles of $\mathrm{Y}$ and $\mathrm{Z}$ respectively are
$1 \mathrm{~L}$ Solution $(\mathrm{X})+\mathrm{AgNO}_{3}$ solution (excess) $\longrightarrow \mathrm{Y}$
$1 \mathrm{~L}$ Solution $(\mathrm{X})+\mathrm{BaCl}_{2}$ solution (excess) $\longrightarrow \mathrm{Z}$
The number of moles of $\mathrm{Y}$ and $\mathrm{Z}$ respectively are
14
The wave function $(\Psi)$ of $2 \mathrm{~s}$ is given by
$$ \Psi_{2 \mathrm{~s}}=\frac{1}{2 \sqrt{2 \pi}}\left(\frac{1}{a_0}\right)^{1 / 2}\left(2-\frac{r}{a_0}\right) e^{-r / 2 a_0} $$
At $r=r_0$, radial node is formed. Thus, $r_0$ in terms of $a_0$
$$ \Psi_{2 \mathrm{~s}}=\frac{1}{2 \sqrt{2 \pi}}\left(\frac{1}{a_0}\right)^{1 / 2}\left(2-\frac{r}{a_0}\right) e^{-r / 2 a_0} $$
At $r=r_0$, radial node is formed. Thus, $r_0$ in terms of $a_0$
15
The strength of 50 volume solution of hydrogen peroxide is ______ $\mathrm{g} / \mathrm{L}$ (Nearest integer).
Given:Molar mass of $\mathrm{H}_{2} \mathrm{O}_{2}$ is $34 \mathrm{~g} \mathrm{~mol}^{-1}$
Molar volume of gas at $\mathrm{STP}=22.7 \mathrm{~L}$
16
A short peptide on complete hydrolysis produces 3 moles of glycine (G), two moles of leucine (L) and two moles of valine (V) per mole of peptide. The number of peptide linkages in it are ________.
17
Number of compounds from the following which will not dissolve in cold $\mathrm{NaHCO}_{3}$ and $\mathrm{NaOH}$ solutions but will dissolve in hot $\mathrm{NaOH}$ solution is ________.
18
An organic compound undergoes first-order decomposition. If the time taken for the $60 \%$ decomposition is $540 \mathrm{~s}$, then the time required for $90 \%$ decomposition will be ________ s. (Nearest integer).
Given: $\ln 10=2.3 ; \log 2=0.3$
Given: $\ln 10=2.3 ; \log 2=0.3$
19
1 mole of ideal gas is allowed to expand reversibly and adiabatically from a temperature of $27^{\circ} \mathrm{C}$. The work done is $3 \mathrm{~kJ} \mathrm{~mol}^{-1}$. The final temperature of the gas is ________ $\mathrm{K}$ (Nearest integer).
Given $\mathrm{C_V}=20 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$
Given $\mathrm{C_V}=20 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$
20
The electrode potential of the following half cell at $298 \mathrm{~K}$
$\mathrm{X}\left|\mathrm{X}^{2+}(0.001 \mathrm{M}) \| \mathrm{Y}^{2+}(0.01 \mathrm{M})\right| \mathrm{Y}$ is _______ $\times 10^{-2} \mathrm{~V}$ (Nearest integer)
Given: $\mathrm{E}^{0} _ {\mathrm{X}^{2+} \mid \mathrm{X}}=-2.36 \mathrm{~V}$
$\mathrm{E}_{\mathrm{Y}^{2+} \mid \mathrm{Y}}^{0}=+0.36 \mathrm{~V}$
$\frac{2.303 \mathrm{RT}}{\mathrm{F}}=0.06 \mathrm{~V}$
$\mathrm{X}\left|\mathrm{X}^{2+}(0.001 \mathrm{M}) \| \mathrm{Y}^{2+}(0.01 \mathrm{M})\right| \mathrm{Y}$ is _______ $\times 10^{-2} \mathrm{~V}$ (Nearest integer)
Given: $\mathrm{E}^{0} _ {\mathrm{X}^{2+} \mid \mathrm{X}}=-2.36 \mathrm{~V}$
$\mathrm{E}_{\mathrm{Y}^{2+} \mid \mathrm{Y}}^{0}=+0.36 \mathrm{~V}$
$\frac{2.303 \mathrm{RT}}{\mathrm{F}}=0.06 \mathrm{~V}$
21
Consider the following equation:
$2 \mathrm{SO}_{2}(g)+\mathrm{O}_{2}(g) \rightleftharpoons 2 \mathrm{SO}_{3}(g), \Delta H=-190 \mathrm{~kJ}$
The number of factors which will increase the yield of $\mathrm{SO}_{3}$ at equilibrium from the following is _______.
A. Increasing temperature
B. Increasing pressure
C. Adding more $\mathrm{SO}_{2}$
D. Adding more $\mathrm{O}_{2}$
E. Addition of catalyst
$2 \mathrm{SO}_{2}(g)+\mathrm{O}_{2}(g) \rightleftharpoons 2 \mathrm{SO}_{3}(g), \Delta H=-190 \mathrm{~kJ}$
The number of factors which will increase the yield of $\mathrm{SO}_{3}$ at equilibrium from the following is _______.
A. Increasing temperature
B. Increasing pressure
C. Adding more $\mathrm{SO}_{2}$
D. Adding more $\mathrm{O}_{2}$
E. Addition of catalyst
22
Lead storage battery contains $38 \%$ by weight solution of $\mathrm{H}_{2} \mathrm{SO}_{4}$. The van't Hoff factor is $2.67$ at this concentration. The temperature in Kelvin at which the solution in the battery will freeze is ________. (Nearest integer).
Given $\mathrm{K}_{f}=1.8 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}$
Given $\mathrm{K}_{f}=1.8 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}$
Mathematics
1
Let $a_{1}=1, a_{2}, a_{3}, a_{4}, \ldots .$. be consecutive natural numbers.
Then $\tan ^{-1}\left(\frac{1}{1+a_{1} a_{2}}\right)+\tan ^{-1}\left(\frac{1}{1+a_{2} a_{3}}\right)+\ldots . .+\tan ^{-1}\left(\frac{1}{1+a_{2021} a_{2022}}\right)$ is equal to :
Then $\tan ^{-1}\left(\frac{1}{1+a_{1} a_{2}}\right)+\tan ^{-1}\left(\frac{1}{1+a_{2} a_{3}}\right)+\ldots . .+\tan ^{-1}\left(\frac{1}{1+a_{2021} a_{2022}}\right)$ is equal to :
2
For $\alpha, \beta \in \mathbb{R}$, suppose the system of linear equations
$$ \begin{aligned} & x-y+z=5 \\ & 2 x+2 y+\alpha z=8 \\ & 3 x-y+4 z=\beta \end{aligned} $$
has infinitely many solutions. Then $\alpha$ and $\beta$ are the roots of :
$$ \begin{aligned} & x-y+z=5 \\ & 2 x+2 y+\alpha z=8 \\ & 3 x-y+4 z=\beta \end{aligned} $$
has infinitely many solutions. Then $\alpha$ and $\beta$ are the roots of :
3
The number of ways of selecting two numbers $a$ and $b, a \in\{2,4,6, \ldots ., 100\}$ and $b \in\{1,3,5, \ldots . ., 99\}$ such that 2 is the remainder when $a+b$ is divided by 23 is :
4
Let $S$ be the set of all values of $a_1$ for which the mean deviation about the mean of 100 consecutive positive integers $a_1, a_2, a_3, \ldots ., a_{100}$ is 25 . Then $S$ is :
5
Let $a, b, c>1, a^3, b^3$ and $c^3$ be in A.P., and $\log _a b, \log _c a$ and $\log _b c$ be in G.P. If the sum of first 20 terms of an A.P., whose first term is $\frac{a+4 b+c}{3}$ and the common difference is $\frac{a-8 b+c}{10}$ is $-444$, then $a b c$ is equal to :
6
Let $f, g$ and $h$ be the real valued functions defined on $\mathbb{R}$ as
$f(x)=\left\{\begin{array}{cc}\frac{x}{|x|}, & x \neq 0 \\ 1, & x=0\end{array}\right.$
$g(x)=\left\{\begin{array}{cc}\frac{\sin (x+1)}{(x+1)}, & x \neq-1 \\ 1, & x=-1\end{array}\right.$
and $h(x)=2[x]-f(x)$, where $[x]$ is the greatest integer $\leq x$. Then the
value of $\lim\limits_{x \rightarrow 1} g(h(x-1))$ is :
$f(x)=\left\{\begin{array}{cc}\frac{x}{|x|}, & x \neq 0 \\ 1, & x=0\end{array}\right.$
$g(x)=\left\{\begin{array}{cc}\frac{\sin (x+1)}{(x+1)}, & x \neq-1 \\ 1, & x=-1\end{array}\right.$
and $h(x)=2[x]-f(x)$, where $[x]$ is the greatest integer $\leq x$. Then the
value of $\lim\limits_{x \rightarrow 1} g(h(x-1))$ is :
7
Let $q$ be the maximum integral value of $p$ in $[0,10]$ for which the roots of the equation $x^2-p x+\frac{5}{4} p=0$ are rational. Then the area of the region $\left\{(x, y): 0 \leq y \leq(x-q)^2, 0 \leq x \leq q\right\}$ is :
8
If the functions $f(x)=\frac{x^3}{3}+2 b x+\frac{a x^2}{2}$
and $g(x)=\frac{x^3}{3}+a x+b x^2, a \neq 2 b$
have a common extreme point, then $a+2 b+7$ is equal to :
and $g(x)=\frac{x^3}{3}+a x+b x^2, a \neq 2 b$
have a common extreme point, then $a+2 b+7$ is equal to :
9
The parabolas : $a x^2+2 b x+c y=0$ and $d x^2+2 e x+f y=0$ intersect on the line $y=1$. If $a, b, c, d, e, f$ are positive real numbers and $a, b, c$ are in G.P., then :
10
Let $\vec{a}$ and $\vec{b}$ be two vectors, Let $|\vec{a}|=1,|\vec{b}|=4$ and $\vec{a} \cdot \vec{b}=2$. If $\vec{c}=(2 \vec{a} \times \vec{b})-3 \vec{b}$, then the value of $\vec{b} \cdot \vec{c}$ is :
11
The range of the function $f(x)=\sqrt{3-x}+\sqrt{2+x}$ is :
12
The solution of the differential equation
$\frac{d y}{d x}=-\left(\frac{x^2+3 y^2}{3 x^2+y^2}\right), y(1)=0$ is :
$\frac{d y}{d x}=-\left(\frac{x^2+3 y^2}{3 x^2+y^2}\right), y(1)=0$ is :
13
Let $x=(8 \sqrt{3}+13)^{13}$ and $y=(7 \sqrt{2}+9)^9$. If $[t]$ denotes the greatest integer $\leq t$, then :
14
Let $A=\{1,2,3,5,8,9\}$. Then the number of possible functions $f: A \rightarrow A$ such that $f(m \cdot n)=f(m) \cdot f(n)$ for every $m, n \in A$ with $m \cdot n \in A$ is equal to ___________.
15
The number of seven digits odd numbers, that can
be formed using all the
seven digits 1, 2, 2, 2, 3, 3, 5 is ____________.
seven digits 1, 2, 2, 2, 3, 3, 5 is ____________.
16
Let $A$ be the area of the region
$\left\{(x, y): y \geq x^2, y \geq(1-x)^2, y \leq 2 x(1-x)\right\}$.
Then $540 \mathrm{~A}$ is equal to :
$\left\{(x, y): y \geq x^2, y \geq(1-x)^2, y \leq 2 x(1-x)\right\}$.
Then $540 \mathrm{~A}$ is equal to :
17
If the value of real number $a>0$ for which $x^2-5 a x+1=0$ and $x^2-a x-5=0$
have a common real root is $\frac{3}{\sqrt{2 \beta}}$ then $\beta$ is equal to ___________.
have a common real root is $\frac{3}{\sqrt{2 \beta}}$ then $\beta$ is equal to ___________.
18
Let $P\left(a_1, b_1\right)$ and $Q\left(a_2, b_2\right)$ be two distinct points on a circle with center $C(\sqrt{2}, \sqrt{3})$. Let $\mathrm{O}$ be the origin and $\mathrm{OC}$ be perpendicular to both $\mathrm{CP}$ and $\mathrm{CQ}$. If the area of the triangle $\mathrm{OCP}$ is $\frac{\sqrt{35}}{2}$, then $a_1^2+a_2^2+b_1^2+b_2^2$ is equal to :
19
Let a line $L$ pass through the point $P(2,3,1)$ and be parallel to the line $x+3 y-2 z-2=0=x-y+2 z$. If the distance of $L$ from the point $(5,3,8)$ is $\alpha$, then $3 \alpha^2$ is equal to :
20
A bag contains six balls of different colours. Two balls are drawn in succession with replacement. The probability that both the balls are of the same colour is p. Next four balls are drawn in succession with replacement and the probability that exactly three balls are of the same colour is $q$. If $p: q=m: n$, where $m$ and $n$ are coprime, then $m+n$ is equal to :
21
If $\int \sqrt{\sec 2 x-1} d x=\alpha \log _e\left|\cos 2 x+\beta+\sqrt{\cos 2 x\left(1+\cos \frac{1}{\beta} x\right)}\right|+$ constant, then $\beta-\alpha$ is equal to ____________.
22
$50^{\text {th }}$ root of a number $x$ is 12 and $50^{\text {th }}$ root of another number $y$ is 18 . Then the remainder obtained on dividing $(x+y)$ by 25 is ____________.
Physics
1
A vehicle travels $4 \mathrm{~km}$ with speed of $3 \mathrm{~km} / \mathrm{h}$ and another $4 \mathrm{~km}$ with speed of $5 \mathrm{~km} / \mathrm{h}$, then its average speed is
2
Match List I with List II:
| List I | List II | ||
|---|---|---|---|
| A. | Torque | I. | $\mathrm{kg} \mathrm{m}^{-1} \mathrm{~s}^{-2}$ |
| B. | Energy density | II. | $\mathrm{kg} \,\mathrm{ms}^{-1}$ |
| C. | Pressure gradient | III. | $\mathrm{kg}\, \mathrm{m}^{-2} \mathrm{~s}^{-2}$ |
| D. | Impulse | IV. | $\mathrm{kg} \,\mathrm{m}^{2} \mathrm{~s}^{-2}$ |
Choose the correct answer from the options given below:
3
An object is allowed to fall from a height $R$ above the earth, where $R$ is the radius of earth. Its velocity when it strikes the earth's surface, ignoring air resistance, will be
4
A force is applied to a steel wire 'A', rigidly clamped at one end. As a result elongation in the wire is $0.2 \mathrm{~mm}$. If same force is applied to another steel wire ' $\mathrm{B}$ ' of double the length and a diameter $2.4$ times that of the wire ' $\mathrm{A}$ ', the elongation in the wire ' $\mathrm{B}$ ' will be (wires having uniform circular cross sections)
5
An electron accelerated through a potential difference $V_{1}$ has a de-Broglie wavelength of $\lambda$. When the potential is changed to $V_{2}$, its de-Broglie wavelength increases by $50 \%$. The value of $\left(\frac{V_{1}}{V_{2}}\right)$ is equal to
6
A machine gun of mass $10 \mathrm{~kg}$ fires $20 \mathrm{~g}$ bullets at the rate of 180 bullets per minute with a speed of $100 \mathrm{~m} \mathrm{~s}^{-1}$ each. The recoil velocity of the gun is
7
The equivalent resistance between $A$ and $B$ is _________.
8
In the given circuit, rms value of current $\left(I_{\mathrm{rms}}\right)$ through the resistor $R$ is:
9
A thin prism $P_1$ with an angle $6^{\circ}$ and made of glass of refractive index $1.54$ is combined with another prism $P_2$ made from glass of refractive index $1.72$ to produce dispersion without average deviation. The angle of prism $P_2$ is
10
A point source of $100 \mathrm{~W}$ emits light with $5 \%$ efficiency. At a distance of $5 \mathrm{~m}$ from the source, the intensity produced by the electric field component is:
11
A block of $\sqrt{3} \mathrm{~kg}$ is attached to a string whose other end is attached to the wall. An unknown force $\mathrm{F}$ is applied so that the string makes an angle of $30^{\circ}$ with the wall. The tension $\mathrm{T}$ is:
(Given $\mathrm{g}=10 \mathrm{~ms}^{-2}$ )
12
As shown in the figure, a point charge $Q$ is placed at the centre of conducting spherical shell of inner radius $a$ and outer radius $b$. The electric field due to charge $\mathrm{Q}$ in three different regions $\mathrm{I}, \mathrm{II}$ and $\mathrm{III}$ is given by:
$(\mathrm{I}: r < a, \mathrm{II}: a < r < b$, III: $r>b$ )
$(\mathrm{I}: r < a, \mathrm{II}: a < r < b$, III: $r>b$ )
13
A flask contains hydrogen and oxygen in the ratio of $2: 1$ by mass at temperature $27^{\circ} \mathrm{C}$. The ratio of average kinetic energy per molecule of hydrogen and oxygen respectively is:
14
As shown in the figure, a current of $2 \mathrm{~A}$ flowing in an equilateral triangle of side $4 \sqrt{3} \mathrm{~cm}$. The magnetic field at the centroid $\mathrm{O}$ of the triangle is
(Neglect the effect of earth's magnetic field)
15
The output $Y$ for the inputs $A$ and $B$ of circuit is given by
Truth table of the shown circuit is:
16
A current carrying rectangular loop PQRS is made of uniform wire. The length $P R=Q S=5 \mathrm{~cm}$ and $P Q=R S=100 \mathrm{~cm}$. If ammeter current reading changes from I to $2 I$, the ratio of magnetic forces per unit length on the wire $P Q$ due to wire $R S$ in the two cases respectively $\left(f_{P Q}^I: f_{P Q}^{2 t}\right)$ is:
17
For a simple harmonic motion in a mass spring system shown, the surface is frictionless. When the mass of the block is $1 \mathrm{~kg}$, the angular frequency is $\omega_{1}$. When the mass block is $2 \mathrm{~kg}$ the angular frequency is $\omega_{2}$. The ratio $\omega_{2} / \omega_{1}$ is
18
In an ac generator, a rectangular coil of 100 turns each having area $14 \times 10^{-2} \mathrm{~m}^{2}$ is rotated at $360 ~\mathrm{rev} / \mathrm{min}$ about an axis perpendicular to a uniform magnetic field of magnitude $3.0 \mathrm{~T}$. The maximum value of the emf produced will be ________ $V$.
$\left(\right.$ Take $\left.\pi=\frac{22}{7}\right)$
$\left(\right.$ Take $\left.\pi=\frac{22}{7}\right)$
19
A faulty thermometer reads $5^{\circ} \mathrm{C}$ in melting ice and $95^{\circ} \mathrm{C}$ in stream. The correct temperature on absolute scale will be __________ $\mathrm{K}$ when the faulty thermometer reads $41^{\circ} \mathrm{C}$.
20
In a Young's double slit experiment, the intensities at two points, for the path differences $\frac{\lambda}{4}$ and $\frac{\lambda}{3}$ ( $\lambda$ being the wavelength of light used) are $I_{1}$ and $I_{2}$ respectively. If $I_{0}$ denotes the intensity produced by each one of the individual slits, then $\frac{I_{1}+I_{2}}{I_{0}}=$ __________.
21
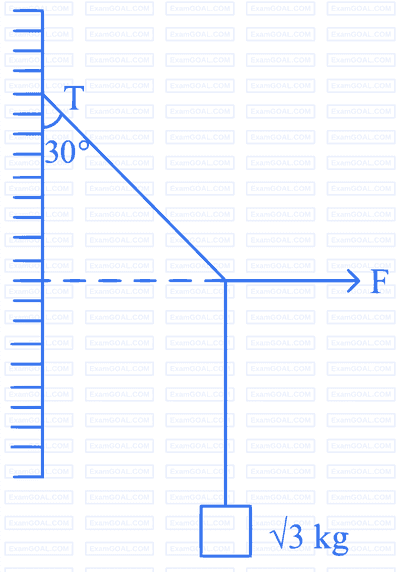
If the potential difference between $\mathrm{B}$ and $\mathrm{D}$ is zero, the value of $x$ is $\frac{1}{n} \Omega$. The value of $n$ is __________.
22
A uniform disc of mass $0.5 \mathrm{~kg}$ and radius $r$ is projected with velocity $18 \mathrm{~m} / \mathrm{s}$ at $\mathrm{t}=0$ s on a rough horizontal surface. It starts off with a purely sliding motion at $\mathrm{t}=0 \mathrm{~s}$. After $2 \mathrm{~s}$ it acquires a purely rolling motion (see figure). The total kinetic energy of the disc after $2 \mathrm{~s}$ will be __________ $\mathrm{J}$ (given, coefficient of friction is $0.3$ and $g=10 \mathrm{~m} / \mathrm{s}^{2}$ ).
23
The velocity of a particle executing SHM varies with displacement $(x)$ as $4 v^{2}=50-x^{2}$. The time period of oscillations is $\frac{x}{7} s$. The value of $x$ is ___________. $\left(\right.$ Take $\left.\pi=\frac{22}{7}\right)$
24
A body of mass $2 \mathrm{~kg}$ is initially at rest. It starts moving unidirectionally under the influence of a source of constant power P. Its displacement in $4 \mathrm{~s}$ is $\frac{1}{3} \alpha^{2} \sqrt{P} m$. The value of $\alpha$ will be ______.
25
As shown in figure, a cuboid lies in a region with electric field $E=2 x^{2} \hat{i}-4 y \hat{j}+6 \hat{k} \mathrm{~N} / \mathrm{C}$. The magnitude of charge within the cuboid is $n \in_{0} C$.
The value of $n$ is _________ (if dimension of cuboid is $1 \times 2 \times 3 \mathrm{~m}^{3}$ )
The value of $n$ is _________ (if dimension of cuboid is $1 \times 2 \times 3 \mathrm{~m}^{3}$ )
26
A stone tied to $180 \mathrm{~cm}$ long string at its end is making 28 revolutions in horizontal circle in every minute. The magnitude of acceleration of stone is $\frac{1936}{x} ms^{-2}$. The value of $x$ ________. (Take $\pi=\frac{22}{7}$ )