JEE Main 2021 (Online) 20th July Morning Shift
Paper was held on
Tue, Jul 20, 2021 3:30 AM
Chemistry
1
According to the valence bond theory the hybridization of central metal atom is dsp2 for which one of the following compounds?
2
The correct structure of Rhumann's Purple, the compound formed in the reaction of ninhydrin with proteins is :
3
The correct order of intensity of colors of the compounds is :
4
The species given below that does NOT show disproportionation reaction is :
5
An inorganic Compound 'X' on treatment with concentrated H2SO4 produces brown fumes and gives dark brown ring with FeSO4 in presence of concentrated H2SO4. Also Compound 'X' gives precipitate 'Y', when its solution in dilute HCl is treated with H2S gas. The precipitate 'Y' on treatment with concentrated HNO3 followed by excess of NH4OH further gives deep blue coloured solution, Compound 'X' is :
6
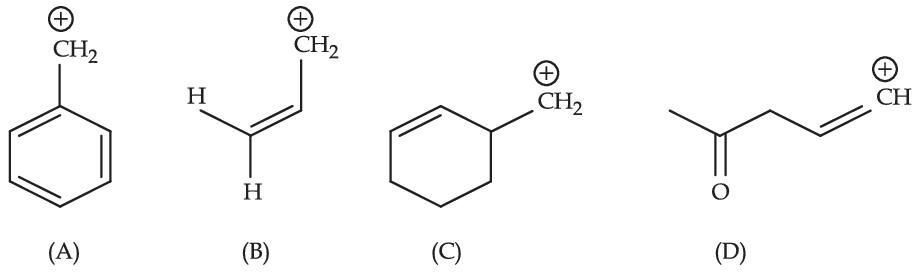
Among the given species the Resonance stabilised carbocations are :
7
In the given reaction
3-Bromo-2, 2-dimethyl butane $$\buildrel {{C_2}{H_5}OH} \over \longrightarrow \mathop {'A'}\limits_{(Major\,\Pr oduct)} $$
Product A is :
3-Bromo-2, 2-dimethyl butane $$\buildrel {{C_2}{H_5}OH} \over \longrightarrow \mathop {'A'}\limits_{(Major\,\Pr oduct)} $$
Product A is :
8
Compound A is converted to B on reaction with CHCl3 and KOH. The compound B is toxic and can be decomposed by C. A, B and C respectively are :
9
Identify the incorrect statement from the following
10
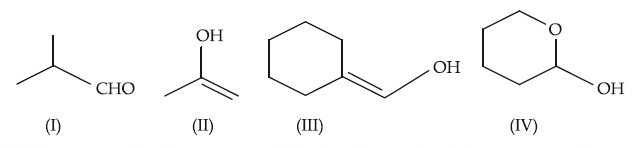
Which among the above compound/s does/do not form Silver mirror when treated with Tollen's reagent?
11
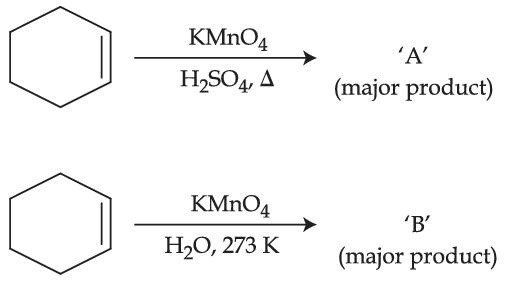
For above chemical reactions, identify the correct statement from the following :
12
The number of lone pairs of electrons on the central I atom in I$$_3^ - $$ is ____________.
13
250 mL of 0.5 M NaOH was added to 500 mL of 1 M HCl. The number of unreacted HCl molecules in the solution after complete reaction is ___________ $$\times$$ 1021. (Nearest integer)
(NA = 6.022 $$\times$$ 1023)
(NA = 6.022 $$\times$$ 1023)
14
The Azimuthal quantum number for the valence electrons of Ga+ ion is ___________.
(Atomic number of Ga = 31)
(Atomic number of Ga = 31)
15
The spin-only magnetic moment value for the complex [Co(CN)6]4$$-$$ is __________ BM.
[At. no. of Co = 27]
[At. no. of Co = 27]
16
2SO2(g) + O2(g) $$\rightleftharpoons$$ 2SO3(g)
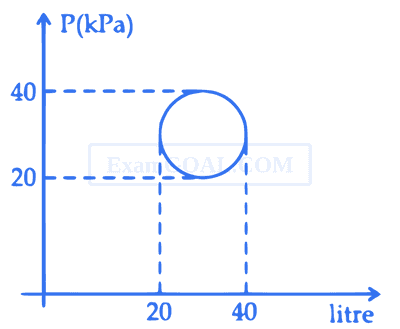
In an equilibrium mixture, the partial pressures are
PSO3 = 43 kPa; PO2 = 530 Pa and PSO2 = 45 kPa. The equilibrium constant KP = ___________ $$\times$$ 10$$-$$2. (Nearest integer)
In an equilibrium mixture, the partial pressures are
PSO3 = 43 kPa; PO2 = 530 Pa and PSO2 = 45 kPa. The equilibrium constant KP = ___________ $$\times$$ 10$$-$$2. (Nearest integer)
17
The number of nitrogen atoms in a semicarbazone molecule of acetone is ______________.
18
To synthesize 1.0 mole of 2-methylpropan-2-ol from Ethylethanoate ___________ equivalents of CH3MgBr Reagent will be required. (Integer value)
19
The inactivation rate of a viral preparation is proportional to the amount of virus. In the first minute after preparation, 10% of the virus is inactivated. The rate constant for viral inactivation is ___________ $$\times$$ 10$$-$$3 min$$-$$1. (Nearest integer)
[Use : ln 10 = 2.303; log10 3 = 0.477; property
of logarithm : log xy = y log x]
[Use : ln 10 = 2.303; log10 3 = 0.477; property
of logarithm : log xy = y log x]
20
An average person needs about 10000 kJ energy per day. The amount of glucose (molar mass = 180.0 g mol$$-$$1) needed to meet this energy requirement is ____________ g.
(Use : $$\Delta$$CH(glucose) = $$-$$2700 kJ mol$$-$$1)
(Use : $$\Delta$$CH(glucose) = $$-$$2700 kJ mol$$-$$1)
21
At 20$$^\circ$$ C, the vapour pressure of benzene is 70 torr and that of methyl benzene is 20 torr. The mole fraction of benzene in the vapour phase at 20$$^\circ$$ above an equimolar mixture of benzene and methyl benzene is _____________ $$\times$$ 10$$-$$2. (Nearest integer)
Mathematics
1
Let a be a positive real number such that $$\int_0^a {{e^{x - [x]}}} dx = 10e - 9$$ where [ x ] is the greatest integer less than or equal to x. Then a is equal to:
2
The mean of 6 distinct observations is 6.5 and their variance is 10.25. If 4 out of 6 observations are 2, 4, 5 and 7, then the remaining two observations are :
3
The value of the integral $$\int\limits_{ - 1}^1 {{{\log }_e}(\sqrt {1 - x} + \sqrt {1 + x} )dx} $$ is equal to:
4
If $$\alpha$$ and $$\beta$$ are the distinct roots of the equation $${x^2} + {(3)^{1/4}}x + {3^{1/2}} = 0$$, then the value of $${\alpha ^{96}}({\alpha ^{12}} - 1) + {\beta ^{96}}({\beta ^{12}} - 1)$$ is equal to :
5
Let $$A = \left[ {\matrix{
2 & 3 \cr
a & 0 \cr
} } \right]$$, a$$\in$$R be written as P + Q where P is a symmetric matrix and Q is skew symmetric matrix. If det(Q) = 9, then the modulus of the sum of all possible values of determinant of P is equal to :
6
If z and $$\omega$$ are two complex numbers such that $$\left| {z\omega } \right| = 1$$ and $$\arg (z) - \arg (\omega ) = {{3\pi } \over 2}$$, then $$\arg \left( {{{1 - 2\overline z \omega } \over {1 + 3\overline z \omega }}} \right)$$ is :
(Here arg(z) denotes the principal argument of complex number z)
(Here arg(z) denotes the principal argument of complex number z)
7
Let [ x ] denote the greatest integer $$\le$$ x, where x $$\in$$ R. If the domain of the real valued function $$f(x) = \sqrt {{{\left| {[x]} \right| - 2} \over {\left| {[x]} \right| - 3}}} $$ is ($$-$$ $$\infty$$, a) $$]\cup$$ [b, c) $$\cup$$ [4, $$\infty$$), a < b < c, then the value of a + b + c is :
8
Let y = y(x) be the solution of the differential equation $$x\tan \left( {{y \over x}} \right)dy = \left( {y\tan \left( {{y \over x}} \right) - x} \right)dx$$, $$ - 1 \le x \le 1$$, $$y\left( {{1 \over 2}} \right) = {\pi \over 6}$$. Then the area of the region bounded by the curves x = 0, $$x = {1 \over {\sqrt 2 }}$$ and y = y(x) in the upper half plane is :
9
Let $$A = [{a_{ij}}]$$ be a 3 $$\times$$ 3 matrix, where $${a_{ij}} = \left\{ {\matrix{
1 & , & {if\,i = j} \cr
{ - x} & , & {if\,\left| {i - j} \right| = 1} \cr
{2x + 1} & , & {otherwise.} \cr
} } \right.$$
Let a function f : R $$\to$$ R be defined as f(x) = det(A). Then the sum of maximum and minimum values of f on R is equal to:
Let a function f : R $$\to$$ R be defined as f(x) = det(A). Then the sum of maximum and minimum values of f on R is equal to:
10
The number of real roots of the equation $${\tan ^{ - 1}}\sqrt {x(x + 1)} + {\sin ^{ - 1}}\sqrt {{x^2} + x + 1} = {\pi \over 4}$$ is :
11
Let y = y(x) be the solution of the differential equation $${e^x}\sqrt {1 - {y^2}} dx + \left( {{y \over x}} \right)dy = 0$$, y(1) = $$-$$1. Then the value of (y(3))2 is equal to :
12
Let 'a' be a real number such that the function f(x) = ax2 + 6x $$-$$ 15, x $$\in$$ R is increasing in $$\left( { - \infty ,{3 \over 4}} \right)$$ and decreasing in $$\left( {{3 \over 4},\infty } \right)$$. Then the function g(x) = ax2 $$-$$ 6x + 15, x$$\in$$R has a :
13
Let a function f : R $$\to$$ R be defined as $$f(x) = \left\{ {\matrix{
{\sin x - {e^x}} & {if} & {x \le 0} \cr
{a + [ - x]} & {if} & {0 < x < 1} \cr
{2x - b} & {if} & {x \ge 1} \cr
} } \right.$$
where [ x ] is the greatest integer less than or equal to x. If f is continuous on R, then (a + b) is equal to:
where [ x ] is the greatest integer less than or equal to x. If f is continuous on R, then (a + b) is equal to:
14
Words with or without meaning are to be formed using all the letters of the word EXAMINATION. The probability that the letter M appears at the fourth position in any such word is :
15
The probability of selecting integers a$$\in$$[$$-$$ 5, 30] such that x2 + 2(a + 4)x $$-$$ 5a + 64 > 0, for all x$$\in$$R, is :
16
Let $$\overrightarrow a $$, $$\overrightarrow b $$, $$\overrightarrow c $$ be three mutually perpendicular vectors of the same magnitude and equally inclined at an angle $$\theta$$, with the vector $$\overrightarrow a $$ + $$\overrightarrow b $$ + $$\overrightarrow c $$. Then 36cos22$$\theta$$ is equal to ___________.
17
Let $$A = \left( {\matrix{
1 & { - 1} & 0 \cr
0 & 1 & { - 1} \cr
0 & 0 & 1 \cr
} } \right)$$ and B = 7A20 $$-$$ 20A7 + 2I, where I is an identity matrix of order 3 $$\times$$ 3. If B = [bij], then b13is equal to _____________.
18
The number of rational terms in the binomial expansion of $${\left( {{4^{{1 \over 4}}} + {5^{{1 \over 6}}}} \right)^{120}}$$ is _______________.
19
If the shortest distance between the lines $$\overrightarrow {{r_1}} = \alpha \widehat i + 2\widehat j + 2\widehat k + \lambda (\widehat i - 2\widehat j + 2\widehat k)$$, $$\lambda$$ $$\in$$ R, $$\alpha$$ > 0 and $$\overrightarrow {{r_2}} = - 4\widehat i - \widehat k + \mu (3\widehat i - 2\widehat j - 2\widehat k)$$, $$\mu$$ $$\in$$ R is 9, then $$\alpha$$ is equal to ____________.
20
Let T be the tangent to the ellipse E : x2 + 4y2 = 5 at the point P(1, 1). If the area of the region bounded by the tangent T, ellipse E, lines x = 1 and x = $$\sqrt 5 $$ is $$\alpha$$$$\sqrt 5 $$ + $$\beta$$ + $$\gamma$$ cos$$-$$1$$\left( {{1 \over {\sqrt 5 }}} \right)$$, then |$$\alpha$$ + $$\beta$$ + $$\gamma$$| is equal to ______________.
21
Let a, b, c, d in arithmetic progression with common difference $$\lambda$$. If $$\left| {\matrix{
{x + a - c} & {x + b} & {x + a} \cr
{x - 1} & {x + c} & {x + b} \cr
{x - b + d} & {x + d} & {x + c} \cr
} } \right| = 2$$, then value of $$\lambda$$2 is equal to ________________.
22
There are 15 players in a cricket team, out of which 6 are bowlers, 7 are batsman and 2 are wicketkeepers. The number of ways, a team of 11 players be selected from them so as to include at least 4 bowlers, 5 batsman and 1 wicketkeeper, is ______________.
23
If the value of $$\mathop {\lim }\limits_{x \to 0} {(2 - \cos x\sqrt {\cos 2x} )^{\left( {{{x + 2} \over {{x^2}}}} \right)}}$$ is equal to ea, then a is equal to __________.
Physics
1
A deuteron and an alpha particle having equal kinetic energy enter perpendicularly into a magnetic field. Let rd and r$$\alpha$$ be their respective radii of circular path. The value of $${{{r_d}} \over {{r_\alpha }}}$$ is equal to :
2
For the circuit shown below, calculate the value of Iz :
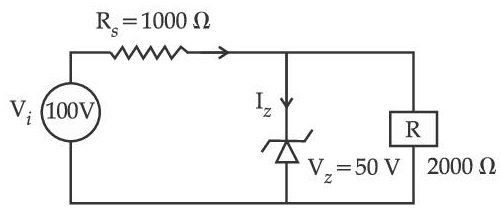

3
A current of 5 A is passing through a non-linear magnesium wire of cross-section 0.04 m2. At every point the direction of current density is at an angle of 60$$^\circ$$ with the unit vector of area of cross-section. The magnitude of electric field at every point of the conductor is :
(Resistivity of magnesium $$\rho$$ = 44 $$\times$$ 10$$-$$8 $$\Omega$$m)
(Resistivity of magnesium $$\rho$$ = 44 $$\times$$ 10$$-$$8 $$\Omega$$m)
4
The normal reaction 'N' for a vehicle of 800 kg mass, negotiating a turn on a 30$$^\circ$$ banked road at maximum possible speed without skidding is ____________ $$\times$$ 103 kg m/s2. [Given cos30$$^\circ$$ = 0.87, $$\mu$$s = 0.2]
5
Consider a mixture of gas molecule of types A, B and C having masses mA < mB < mC. The ratio of their root mean square speeds at normal temperature and pressure is :
6
The amount of heat needed to raise the temperature of 4 moles of rigid diatomic gas from 0$$^\circ$$ C to 50$$^\circ$$ C when no work is done is ___________. (R is the universal gas constant).
7
A butterfly is flying with a velocity $$4\sqrt 2 $$ m/s in North-East direction. Wind is slowly blowing at 1 m/s from North to South. The resultant displacement of the butterfly in 3 seconds is :
8
A certain charge Q is divided into two parts q and (Q $$-$$ q). How should the charges Q and q be divided so that q and (Q $$-$$ q) placed at a certain distance apart experience maximum electrostatic repulsion?
9
The arm PQ of a rectangular conductor is moving from x = 0 to x = 2b outwards and then inwards from x = 2b to x = 0 as shown in the figure. A uniform magnetic field perpendicular to the plane is acting from x = 0 to x = b. Identify the graph showing the variation of different quantities with distance.
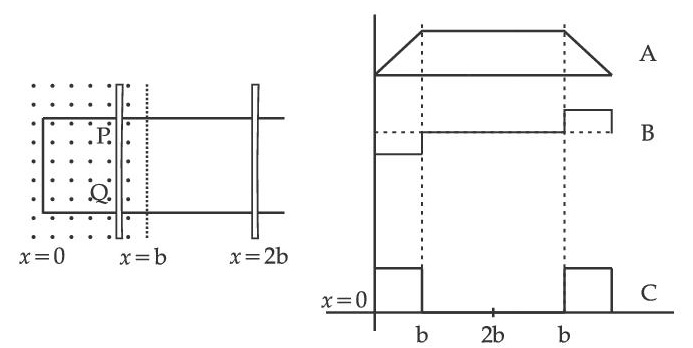

10

The value of current in the 6 $$\Omega$$ resistance is :
11
A steel block of 10 kg rests on a horizontal floor as shown. When three iron cylinders are placed on it as shown, the block and cylinders go down with an acceleration 0.2 m/s2. The normal reaction R' by the floor if mass of the iron cylinders are equal and of 20 kg each, is ____________ N. [Take g = 10 m/s2 and $$\mu$$s = 0.2]


12
A nucleus of mass M emits $$\gamma$$ -ray photon of frequency 'v'. The loss of internal energy by the nucleus is :
[Take 'c' as the speed of electromagnetic wave]
[Take 'c' as the speed of electromagnetic wave]
13
The radiation corresponding to 3 $$\to$$ 2 transition of a hydrogen atom falls on a gold surface to generate photoelectrons. The electrons are passed through a magnetic field of 5 $$\times$$ 10$$-$$4 T. Assume that the radius of the largest circular path followed by these electrons is 7 mm, the work function of the metal is : (Mass of electron = 9.1 $$\times$$ 10$$-$$31 kg)
14
If $$\overrightarrow A $$ and $$\overrightarrow B $$ are two vectors satisfying the relation $$\overrightarrow A $$ . $$\overrightarrow B $$ = $$\left| {\overrightarrow A \times \overrightarrow B } \right|$$. Then the value of $$\left| {\overrightarrow A - \overrightarrow B } \right|$$ will be :
15
The entropy of any system is given by
$$S = {\alpha ^2}\beta \ln \left[ {{{\mu kR} \over {J{\beta ^2}}} + 3} \right]$$ where $$\alpha$$ and $$\beta$$ are the constants. $$\mu$$, J, k and R are no. of moles, mechanical equivalent of heat, Boltzmann constant and gas constant respectively.
[Take $$S = {{dQ} \over T}$$]
Choose the incorrect option from the following :
$$S = {\alpha ^2}\beta \ln \left[ {{{\mu kR} \over {J{\beta ^2}}} + 3} \right]$$ where $$\alpha$$ and $$\beta$$ are the constants. $$\mu$$, J, k and R are no. of moles, mechanical equivalent of heat, Boltzmann constant and gas constant respectively.
[Take $$S = {{dQ} \over T}$$]
Choose the incorrect option from the following :
16
AC voltage V(t) = 20 sin$$\omega$$t of frequency 50 Hz is applied to a parallel plate capacitor. The separation between the plates is 2 mm and the area is 1 m2. The amplitude of the oscillating displacement current for the applied AC voltage is _________. [Take $$\varepsilon $$0 = 8.85 $$\times$$ 10$$-$$12 F/m]
17
Region I and II are separated by a spherical surface of radius 25 cm. An object is kept in region I at a distance of 40 cm from the surface. The distance of the image from the surface is :
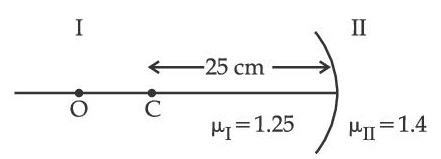

18
A person whose mass is 100 kg travels from Earth to Mars in a spaceship. Neglect all other objects in sky and take acceleration due to gravity on the surface of the Earth and Mars as 10 m/s2 and 4 m/s2 respectively. Identify from the below figures, the curve that fits best for the weight of the passenger as a function of time.
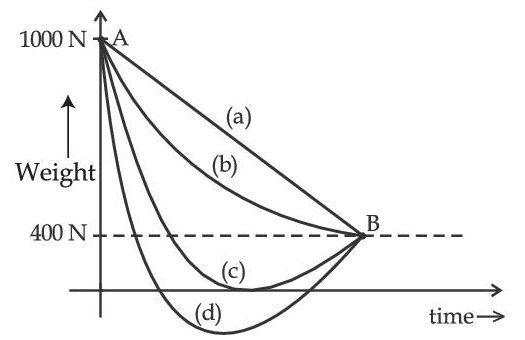

19
The value of tension in a long thin metal wire has been changed from T1 to T2. The lengths of the metal wire at two different values of tension T1 and T2 are l1 and l2 respectively. The actual length of the metal wire is :
20
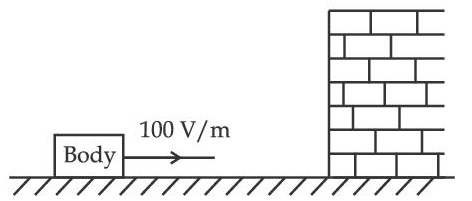
A body having specific charge 8 $$\mu$$C/g is resting on a frictionless plane at a distance 10 cm from the wall (as shown in the figure). It starts moving towards the wall when a uniform electric field of 100 V/m is applied horizontally towards the wall. If the collision of the body with the wall is perfectly elastic, then the time period of the motion will be _______________ s.

21
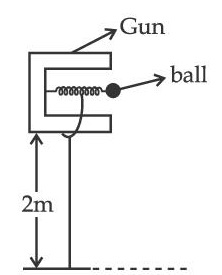
In a spring gun having spring constant 100 N/m a small ball 'B' of mass 100 g is put in its barrel (as shown in figure) by compressing the spring through 0.05 m. There should be a box placed at a distance 'd' on the ground so that the ball falls in it. If the ball leaves the gun horizontally at a height of 2 m above the ground. The value of d is _________ m. (g = 10 m/s2).

22
An object viewed from a near point distance of 25 cm, using a microscopic lens with magnification '6', gives an unresolved image. A resolved image is observed at infinite distance with a total magnification double the earlier using an eyepiece along with the given lens and a tube of length 0.6 m, if the focal length of the eyepiece is equal to __________ cm.
23
A circular disc reaches from top to bottom of an inclined plane of length 'L'. When it slips down the plane, it makes time 't1'. When it rolls down the plane, it takes time t2. The value of $${{{t_2}} \over {{t_1}}}$$ is $$\sqrt {{3 \over x}} $$. The value of x will be _______________.
24
The amplitude of wave disturbance propagating in the positive x-direction is given by $$y = {1 \over {{{(1 + x)}^2}}}$$ at time t = 0 and $$y = {1 \over {1 + {{(x - 2)}^2}}}$$ at t = 1 s, where x and y are in metres. The shape of wave does not change during the propagation. The velocity of the wave will be ___________ m/s.
25
In an LCR series circuit, an inductor 30 mH and a resistor 1 $$\Omega$$ are connected to an AC source of angular frequency 300 rad/s. The value of capacitance for which, the current leads the voltage by 45$$^\circ$$ is $${1 \over x} \times {10^{ - 3}}$$ F. Then the value of x is ____________.
26
A rod of mass M and length L is lying on a horizontal frictionless surface. A particle of mass 'm' travelling along the surface hits at one end of the rod with a velocity 'u' in a direction perpendicular to the rod. The collision is completely elastic. After collision, particle comes to rest. The ratio of masses $$\left( {{m \over M}} \right)$$ is $${1 \over x}$$. The value of 'x' will be ____________.
27
In the reported figure, heat energy absorbed by a system in going through a cyclic process is ___________ $$\pi$$J.