JEE Main 2020 (Online) 4th September Morning Slot
Paper was held on
Fri, Sep 4, 2020 3:30 AM
Chemistry
1
The IUPAC name of the following compound is :


2
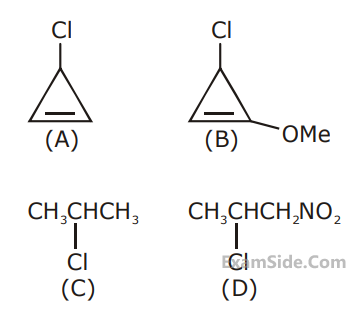
The decreasing order of reactivity of the
following organic molecules towards AgNO3
solution is :

3
For one mole of an ideal gas, which of these
statements must be true?
(a) U and H each depends only on temperature
(b) Compressibility factor z is not equal to 1
(c) CP, m – CV, m = R
(d) dU = CVdT for any process
(a) U and H each depends only on temperature
(b) Compressibility factor z is not equal to 1
(c) CP, m – CV, m = R
(d) dU = CVdT for any process
4
The elements with atomic numbers 101 and 104
belong to, respectively :
5
The pair in which both the species have the
same magnetic moment (spin only) is :
6
The mass of ammonia in grams produced when
2.8 kg of dinitrogen quantitatively reacts with 1
kg of dihydrogen is _______.
7
A 20.0 mL solution containing 0.2 g impure
H2O2 reacts completely with 0.316 g of KMnO4
in acid solution. The purity of H2O2 (in %) is
_____________
(mol. wt. of H2O2 = 34; mol. wt. of KMnO4 = 158)
(mol. wt. of H2O2 = 34; mol. wt. of KMnO4 = 158)
8
At 300 K, the vapour pressure of a solution
containing 1 mole of n-hexane and 3 moles of
n-heptane is 550 mm of Hg. At the same
temperature, if one more mole of n-heptane is
added to this solution, the vapour pressure of
the solution increases by 10 mm of Hg. What is
the vapour pressure in mm Hg of n-heptane in
its pure state ______?
9
If 75% of a first order reaction was completed
in 90 minutes, 60% of the same reaction would
be completed in approximately (in minutes)
_______.
(Take : log 2 = 0.30; log 2.5 = 0.40)
(Take : log 2 = 0.30; log 2.5 = 0.40)
10
The number of chiral centres present in [B] is
_____.
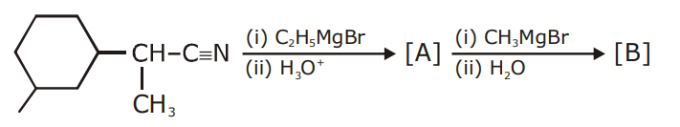
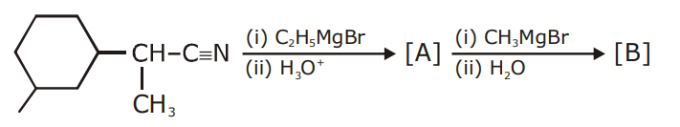
11
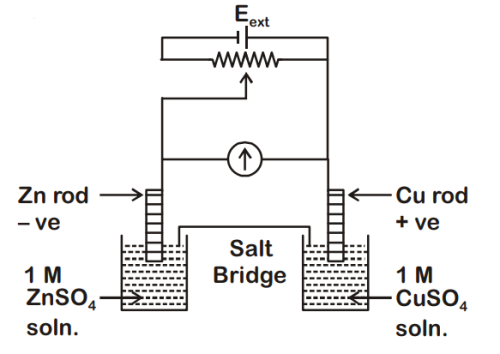
$$E_{C{u^{2 + }}|Cu}^0$$ = +0.34 V
$$E_{Z{n^{2 + }}|Zn}^0$$ = -0.76 V
Identify the incorrect statement from the option below for the above cell :
12
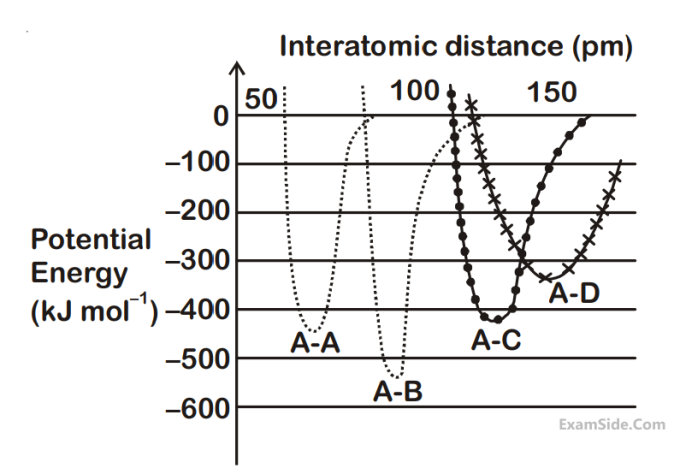
The intermolecular potential energy for the
molecules A, B, C and D given below suggests
that :

13
Which of the following will react with CHCl3 +
alc. KOH?
14
The number of isomers possible for
[Pt(en)(NO2)2] is :
[Pt(en)(NO2)2] is :
15
[P] on treatment with Br2/FeBr3 in CCl4
produced a single isomer C8H7O2Br while
heating [P] with sodalime gave toluene. The
compound [P] is
16
When neopentyl alcohol is heated with an acid,
it slowly converted into an 85 : 15 mixture of
alkenes A and B, respectively. What are these
alkenes?
17
The ionic radii of O2–, F–, Na+ and Mg2+ are in
the order :
18
The region in the electromagnetic spectrum
where the Balmar series lines appear is :
19
For the equilibrium A ⇌ B , the variation of the
rate of the forward (a) and reverse (b) reaction
with time is given by :
20
An organic compound (A) (molecular formula
C6H12O2) was hydrolysed with dil. H2SO4 to give
a carboxylic acid (B) and an alcohol (C). ‘C’
gives white turbidity immediately when treated
with anhydrous ZnCl2 and conc. HCl. The
organic compound (A) is :
21
What are the functional groups present in the
structure of maltose?
Mathematics
1
A survey shows that 63% of the people in a city read newspaper A whereas 76% read
newspaper B. If x% of the people read both the newspapers, then a possible value of x can be:
2
The probability of a man hitting a target is $${1 \over {10}}$$. The least number of shots required, so that the
probability of his hitting the target at least once is greater than $${1 \over {4}}$$, is ____________.
3
Let $${\left( {2{x^2} + 3x + 4} \right)^{10}} = \sum\limits_{r = 0}^{20} {{a_r}{x^r}} $$
Then $${{{a_7}} \over {{a_{13}}}}$$ is equal to ______.
Then $${{{a_7}} \over {{a_{13}}}}$$ is equal to ______.
4
If the system of equations
x - 2y + 3z = 9
2x + y + z = b
x - 7y + az = 24,
has infinitely many solutions, then a - b is equal to.........
x - 2y + 3z = 9
2x + y + z = b
x - 7y + az = 24,
has infinitely many solutions, then a - b is equal to.........
5
Suppose a differentiable function f(x) satisfies the identity
f(x+y) = f(x) + f(y) + xy2 + x2y, for all real x and y.
$$\mathop {\lim }\limits_{x \to 0} {{f\left( x \right)} \over x} = 1$$, then f'(3) is equal to ______.
f(x+y) = f(x) + f(y) + xy2 + x2y, for all real x and y.
$$\mathop {\lim }\limits_{x \to 0} {{f\left( x \right)} \over x} = 1$$, then f'(3) is equal to ______.
6
If $$\left( {a + \sqrt 2 b\cos x} \right)\left( {a - \sqrt 2 b\cos y} \right) = {a^2} - {b^2}$$
where a > b > 0, then $${{dx} \over {dy}}\,\,at\left( {{\pi \over 4},{\pi \over 4}} \right)$$ is :
where a > b > 0, then $${{dx} \over {dy}}\,\,at\left( {{\pi \over 4},{\pi \over 4}} \right)$$ is :
7
Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A
and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m)
above the line AC is :
8
The mean and variance of 8 observations are 10 and 13.5, respectively. If 6 of these observations
are 5, 7, 10, 12, 14, 15, then the absolute difference of the remaining two observations is :
9
If $$A = \left[ {\matrix{
{\cos \theta } & {i\sin \theta } \cr
{i\sin \theta } & {\cos \theta } \cr
} } \right]$$, $$\left( {\theta = {\pi \over {24}}} \right)$$
and $${A^5} = \left[ {\matrix{ a & b \cr c & d \cr } } \right]$$, where $$i = \sqrt { - 1} $$ then which one of the following is not true?
and $${A^5} = \left[ {\matrix{ a & b \cr c & d \cr } } \right]$$, where $$i = \sqrt { - 1} $$ then which one of the following is not true?
10
Let $$u = {{2z + i} \over {z - ki}}$$, z = x + iy and k > 0. If the curve represented
by Re(u) + Im(u) = 1 intersects the y-axis at the points P and Q where PQ = 5, then the value of k is :
by Re(u) + Im(u) = 1 intersects the y-axis at the points P and Q where PQ = 5, then the value of k is :
11
Let $$\alpha $$ and $$\beta $$ be the roots of x2 - 3x + p=0 and $$\gamma $$ and $$\delta $$ be the roots of x2 - 6x + q = 0. If $$\alpha, \beta, \gamma, \delta $$
form a geometric progression.Then ratio (2q + p) : (2q - p) is:
12
Let f be a twice differentiable function on (1, 6). If f(2) = 8, f’(2) = 5, f’(x) $$ \ge $$ 1 and f''(x) $$ \ge $$ 4, for all x $$ \in $$ (1, 6), then :
13
Let $$f\left( x \right) = \int {{{\sqrt x } \over {{{\left( {1 + x} \right)}^2}}}dx\left( {x \ge 0} \right)} $$. Then f(3) – f(1) is eqaul to :
14
Let $$f(x) = \left| {x - 2} \right|$$ and g(x) = f(f(x)), $$x \in \left[ {0,4} \right]$$. Then
$$\int\limits_0^3 {\left( {g(x) - f(x)} \right)} dx$$ is equal to:
$$\int\limits_0^3 {\left( {g(x) - f(x)} \right)} dx$$ is equal to:
15
The integral $$\int {{{\left( {{x \over {x\sin x + \cos x}}} \right)}^2}dx} $$ is equal to
(where C is a constant of integration):
(where C is a constant of integration):
16
Let $${{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1$$ (a > b) be a given ellipse, length of whose latus rectum is 10. If its eccentricity is the maximum value of the function,
$$\phi \left( t \right) = {5 \over {12}} + t - {t^2}$$, then a2 + b2 is equal to :
$$\phi \left( t \right) = {5 \over {12}} + t - {t^2}$$, then a2 + b2 is equal to :
17
Let y = y(x) be the solution of the differential equation,
xy'- y = x2(xcosx + sinx), x > 0. if y ($$\pi $$) = $$\pi $$ then
$$y''\left( {{\pi \over 2}} \right) + y\left( {{\pi \over 2}} \right)$$ is equal to :
xy'- y = x2(xcosx + sinx), x > 0. if y ($$\pi $$) = $$\pi $$ then
$$y''\left( {{\pi \over 2}} \right) + y\left( {{\pi \over 2}} \right)$$ is equal to :
18
Let [t] denote the greatest integer $$ \le $$ t. Then the equation in x,
[x]2 + 2[x+2] - 7 = 0 has :
[x]2 + 2[x+2] - 7 = 0 has :
Physics
1
A two point charges 4q and -q are fixed
on the x-axis at x = $$ - {d \over 2}$$
and x = $${d \over 2}$$
respectively. If a third point charge 'q' is taken from the origin to x = d along the semicircle as shown in the figure, the energy of the charge will :


2
Dimensional formula for thermal conductivity is (here K denotes the temperature):
3
Starting from the origin at time t = 0, with initial velocity 5$$\widehat j$$ ms-1 , a particle moves in the x-y plane
with a constant acceleration of $$\left( {10\widehat i + 4\widehat j} \right)$$ ms-2. At time t, its coordinates are (20 m, y0
m). The
values of t and y0 are, respectively:
4
Choose the correct option relating wave lengths of different parts of electromagnetic wave spectrum:
5
Given figure shows few data points in a phot electric effect experiment for a certain metal. The
minimum energy for ejection of electron from its surface is:
(Plancks constant h = 6.62 × 10–34 J.s)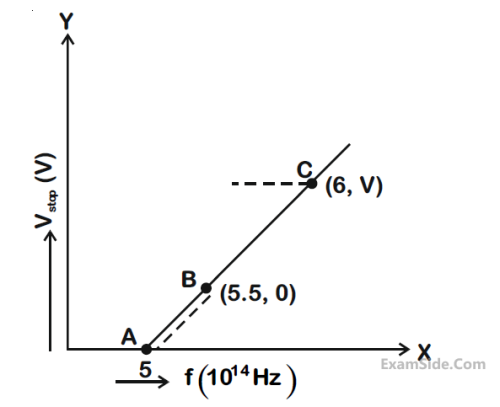
(Plancks constant h = 6.62 × 10–34 J.s)

6
A air bubble of radius 1 cm in water has an upward acceleration 9.8 cm s–2. The density of water is
1 gm cm–3 and water offers negligible drag force on the bubble. The mass of the bubble is (g = 980
cm/s2).
7
A Tennis ball is released from a height h and after freely falling on a wooden floor
it rebounds and reaches height $${h \over 2}$$. The
velocity versus height of the ball during its motion may be represented graphically by :
(graph are drawn schematically and on not to scale)
(graph are drawn schematically and on not to scale)
8
Particle A of mass mA = $${m \over 2}$$ moving along the x-axis with velocity v0 collides elastically with another particle B at rest having mass mB = $${m \over 3}$$. If both particles move along the x-axis after the collision, the change $$\Delta $$$$\lambda $$ in de-Broglie wavlength of particle A, in terms of its de-Broglie wavelength ($$\lambda $$0) before collision is :
9
A battery of 3.0 V is connected to a resistor dissipating 0.5 W of power. If the terminal voltage of the battery is 2.5 V, the power dissipated within the internal resistance is :
10
Blocks of masses m, 2m, 4m and 8m are arranged in a line on a frictionless floor. Another block of
mass m, moving with speed v along the same line (see figure) collides with mass m in perfectly
inelastic manner. All the subsequent collisions are also perfectly inelastic. By the time the last block
of mass 8m starts moving the total energy loss is p% of the original energy. Value of 'p' is close to :
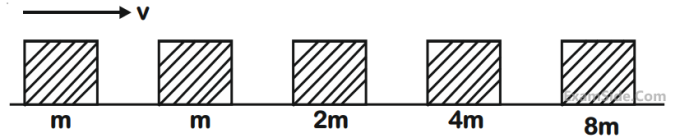

11
For a transverse wave travelling along a straight line, the distance between two peaks (crests) is 5 m, while the distance between one crest and one trough is 1.5 m. The possible wavelengths (in m) of the are :
12
A small bar magnet is moved through a coil at constant speed from one end to the other. Which of the following series of observations will be seen on the galvanometer G attached across the coil?
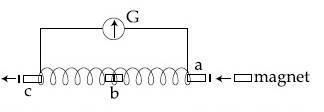
Three positions shown describe :
(a) the magnet's entry
(b) magnet is completely inside and
(c) magnet's exit.

Three positions shown describe :
(a) the magnet's entry
(b) magnet is completely inside and
(c) magnet's exit.
13
A wire A, bent in the shape of an arc of a circle, carrying a current of 2 A and having radius 2 cm and another wire B, also bent in the shape of arc of a circle, carrying a current of 3 A and having radius of 4 cm, are placed as shown in the figure. The ratio of the magnetic fields due to the wires A and B at the common centre O is :
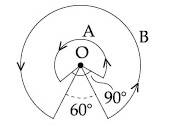

14
Match the $${{{C_P}} \over {{C_V}}}$$ ratio for ideal gases with different type of molecules :
| Molecule Type | CP/CV |
|---|---|
| (A) Monatomic | (I) 7/5 |
| (B) Diatomic rigid molecules | (II) 9/7 |
| (C) Diatomic non-rigid molecules | (III) 4/3 |
| (D) Triatomic rigid molecules | (IV) 5/3 |
15
A beam of plane polarised light of large
cross-sectional area and uniform intensity
of 3.3 Wm-2 falls normally on a
polariser (cross sectional area 3 $$ \times $$ 10-4 m2) which
rotates about its axis with an angular speed
of 31.4 rad/s. The energy of light passing through
the polariser per revolution, is close to :
cross-sectional area and uniform intensity
of 3.3 Wm-2 falls normally on a
polariser (cross sectional area 3 $$ \times $$ 10-4 m2) which
rotates about its axis with an angular speed
of 31.4 rad/s. The energy of light passing through
the polariser per revolution, is close to :
16
The specific heat of water
= 4200 J kg-1K-1 and the latent heat of
ice = 3.4 $$ \times $$ 105 J kg–1. 100 grams of ice at
0oC is placed in 200 g of water at 25oC. The
amount of ice that will melt as the temperature
of water reaches 0oC is close to (in grams) :
= 4200 J kg-1K-1 and the latent heat of
ice = 3.4 $$ \times $$ 105 J kg–1. 100 grams of ice at
0oC is placed in 200 g of water at 25oC. The
amount of ice that will melt as the temperature
of water reaches 0oC is close to (in grams) :
17
Take the breakdown voltage of the
zener diode used in the given circuit as 6V.
For the input voltage shown in figure below,
the time variation of the output voltage is:
(Graphs drawn are schematic and not to scale)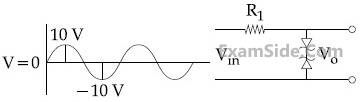
zener diode used in the given circuit as 6V.
For the input voltage shown in figure below,
the time variation of the output voltage is:
(Graphs drawn are schematic and not to scale)
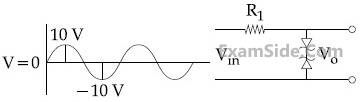
18
A small bar magnet placed with its axis
at 30o with an external field of 0.06 T
experiences a torque of 0.018 Nm. The
minimum work required to rotate it from its
stable to unstable equilibrium position is :
at 30o with an external field of 0.06 T
experiences a torque of 0.018 Nm. The
minimum work required to rotate it from its
stable to unstable equilibrium position is :
19
Two charged thin infinite plane sheets of
uniform surface charge density $${\sigma _ + }$$ and $${\sigma _ - }$$,
where |$${\sigma _ + }$$| > |$${\sigma _ - }$$|, intersect at right angle.
Which of the following best represents the
electric field lines for this system :
uniform surface charge density $${\sigma _ + }$$ and $${\sigma _ - }$$,
where |$${\sigma _ + }$$| > |$${\sigma _ - }$$|, intersect at right angle.
Which of the following best represents the
electric field lines for this system :
20
In a compound microscope, the magnified virtual image is formed at a distance of 25 cm from the
eye-piece. The focal length of its objective lens is 1 cm. If the magnification is 100 and the tube
length of the microscope is 20 cm, then the focal length of the eye-piece lens (in cm) is __________.
21
A circular disc of mass M and radius R is rotating about its axis with angular speed $${\omega _1}$$
. If another
stationary disc having radius $${R \over 2}$$ and same mass M is droped co-axially on to the rotating disc.
Gradually both discs attain constant angular speed $${\omega _2}$$
the energy lost in the process is p% of the
initial energy. Value of p is __________.
22
A closed vessel contains 0.1 mole of a monoatomic ideal gas at 200 K. If 0.05 mole of the same gas
at 400 K is added to it, the final equilibrium temperature (in K) of the gas in the vessel will be close
to _______.
23
On the x-axis and at a distance x from the origin, the gravitational field due a mass distribution is
given by $${{Ax} \over {{{\left( {{x^2} + {a^2}} \right)}^{3/2}}}}$$ in the x-direction. The magnitude of gravitational potential on the x-axis at a
distance x, taking its value to be zero at infinity, is: