Chemistry
CH3 - CH = CH - CH3 $$\buildrel {{O_3}} \over \longrightarrow $$ A $$\mathrel{\mathop{\kern0pt\longrightarrow} \limits_{Zn}^{H{}_2O}} $$ B
The compound B is
a. CO (g) + H2O (g) $$\leftrightharpoons$$ CO2(g) + H2 (g) ; K1
b. CH4 (g) + H2O (g) $$\leftrightharpoons$$ CO(g) + 3H2 (g) ; K2
c. CH4 (g) + 2H2O (g) $$\leftrightharpoons$$ CO2(g) + 4H2 (g) ; K3
i. $$HCO_3^−$$
ii. $$H_3O^+$$
iii. $$HSO_4^−$$
iv. $$HSO_3F$$
Which one of the following is the correct sequence of their acid strength?
$${1 \over 2} X_2$$ + $${3 \over 2} Y_2 \to$$ XY3, $$\Delta H$$ = -30 kJ, to be at equilibrium, the temperature will be :
$${1 \over 2}C{l_2}(g)$$ $$\buildrel {{1 \over 2}{\Delta _{diss}}{H^\Theta }} \over \longrightarrow $$ $$Cl(g)$$ $$\buildrel {{\Delta _{eg}}{H^\Theta }} \over \longrightarrow $$ $$C{l^ - }(g)$$ $$\buildrel {{\Delta _{Hyd}}{H^\Theta }} \over \longrightarrow $$ $$C{l^ - }(aq)$$
(Using the data, $${\Delta _{diss}}H_{C{l_2}}^\Theta $$ = 240 kJ/mol, $${\Delta _{eg}}H_{Cl}^\Theta $$ = -349 kJ/mol, $${\Delta _{hyd}}H_{C{l^ - }}^\Theta $$ = - 381 kJ/mol) will be :
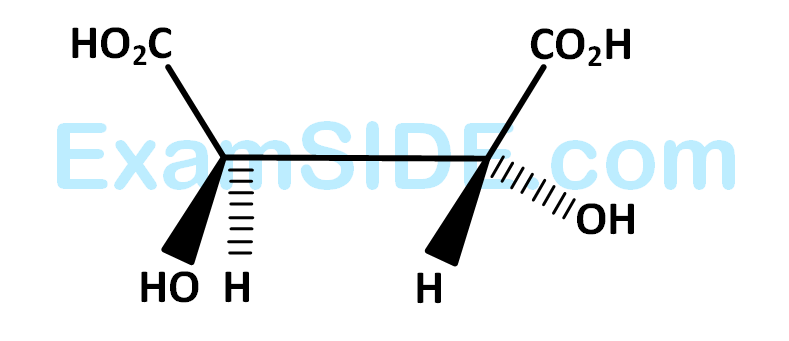
Mathematics
Then which one of the following is true?
Y = { y $$ \in $$ N, y = 4x + 3 for some x $$ \in $$ N }.
Show that f is invertible and its inverse is
$$P\left( A \right) = {1 \over 4},P\left( {A|B} \right) = {1 \over 2}$$ and $$P\left( {B|A} \right) = {2 \over 3}.$$ Then $$P(B)$$ is :
$${{dy} \over {dx}} = {{x + y} \over x}$$ satisfying the condition $$y(1)=1$$ is :
Statement-1 : If $$A \ne I$$ and $$A \ne - I$$, then det$$(A)=-1$$
Statement- 2 : If $$A \ne I$$ and $$A \ne - I$$, then tr $$(A)$$ $$ \ne 0$$.
where $$p>0$$ and $$q>0$$. Then which one of the following holds?
$${x^7} + 14{x^5} + 16{x^3} + 30x - 560 = 0$$ have?
Statement - 1: The number of different ways the child can buy the six ice-cream is $${}^{10}{C_5}$$.
Statement - 2: The number of different ways the child can buy the six ice-cream is equal to the number of different ways of arranging 6 A and 4 B's in a row.
STATEMENT - 2 : For every natural number $$n \ge 2,$$, $$$\sqrt {n\left( {n + 1} \right)} < n + 1.$$$
$$S = \left\{ {(x,y):y = x + 1\,\,and\,\,0 < x < 2} \right\}$$
$$T = \left\{ {(x,y): x - y\,\,\,is\,\,an\,\,{\mathop{\rm int}} eger\,} \right\}$$,
Which one of the following is true ?
Physics
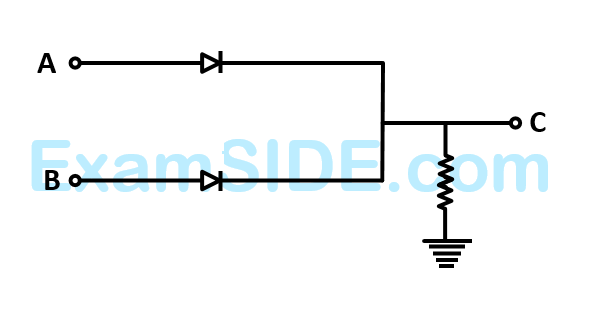
The circuit represents
Then which of the following is true?
Statement- 1:
Energy is released when heavy nuclei undergo fission or light nuclei undergo fusion and
Statement- 2:
For heavy nuclei, binding energy per nucleon increases with increasing $$Z$$ while for light nuclei it decreases with increasing $$Z.$$
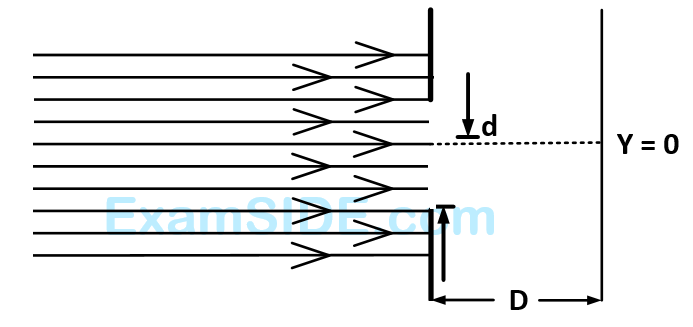
Which of the following graphs can be expected to represent the number of electrons $$'N'$$ detected as a function of the detector position $$'y'\left( {y = 0} \right.$$ corresponds to the middle of the slit$$\left. \, \right)$$
$$\left( {{\mu _0} = 4\pi \times {{10}^{ - 7}}\,Tm\,{A^{ - 1}}} \right)$$
$$\left( {{\mu _0} = 4\pi \times {{10}^{ - 7}}\,\,Tm\,\,{A^{ - 1}}} \right)$$
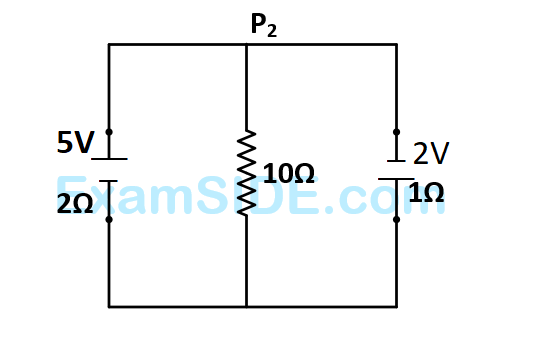
The current in the $$10\Omega $$ resistor is
(i) Take current $$'I'$$ entering from $$'A'$$ and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field $$E(r)$$ at distance $$'r'$$ from A by using Ohm's law $$E = \rho j,$$ where $$j$$ is the current per unit area at $$'r'$$.
(iii) From the $$'r'$$ dependence of $$E(r)$$, obtain the potential $$V(r)$$ at $$r$$.
(iv) Repeat (i), (ii) and (iii) for current $$'I'$$ leaving $$'D'$$ and superpose results for $$'A'$$ and $$'D'.$$

$$\Delta V$$ measured between $$B$$ and $$C$$ is
(i) Take current $$'I'$$ entering from $$'A'$$ and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field $$E(r)$$ at distance $$'r'$$ from A by using Ohm's law $$E = \rho j,$$ where $$j$$ is the current per unit area at $$'r'$$.
(iii) From the $$'r'$$ dependence of $$E(r)$$, obtain the potential $$V(r)$$ at $$r$$.
(iv) Repeat (i), (ii) and (iii) for current $$'I'$$ leaving $$'D'$$ and superpose results for $$'A'$$ and $$'D'.$$

For current entering at $$A,$$ the electric field at a distance $$'r'$$ from $$A$$ is
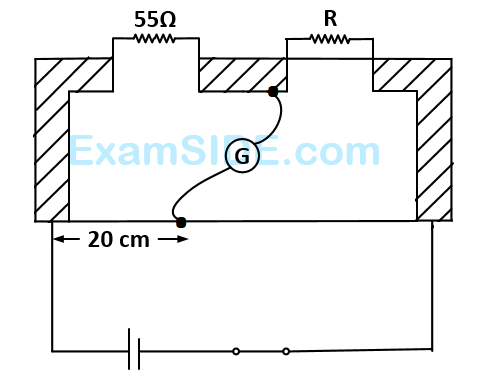
The value of the unknown resister $$R$$ is
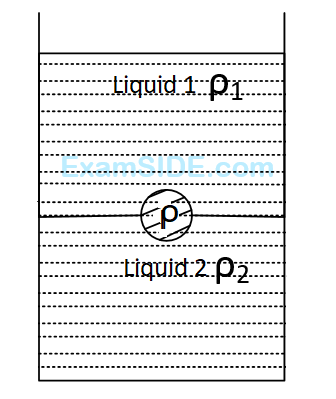
Statement - $$1$$:
For a mass $$M$$ kept at the center of a cube of side $$'a'$$, the flux of gravitational field passing through its sides $$4\,\pi \,GM.$$
Statement - 2:
If the direction of a field due to a point source is radial and its dependence on the distance $$'r'$$ from the source is given as $${1 \over {{r^2}}},$$ its flux through a closed surface depends only on the strength of the source enclosed by the surface and not on the size or shape of the surface.