JEE Main 2018 (Online) 16th April Morning Slot
Paper was held on
Mon, Apr 16, 2018 3:30 AM
Chemistry
1
In a complexometric titration of metal ion with ligand
M(Metal ion) + L(Ligand) $$ \to $$ C(Complex) end point is estimated spectrophoto - metrically (through light absorption). If 'M' and 'C' do not absorb light and only 'L' absorbs, then the titration plot between absorbed light (A) versus volume of ligand 'L' (V) would look like :
M(Metal ion) + L(Ligand) $$ \to $$ C(Complex) end point is estimated spectrophoto - metrically (through light absorption). If 'M' and 'C' do not absorb light and only 'L' absorbs, then the titration plot between absorbed light (A) versus volume of ligand 'L' (V) would look like :
2
The major product of the following reaction is :


3
The most polar compound among the following is :
4
The major product B formed in the following reaction sequence is :


5
The major product of the following reaction is :


6
The major product of the following reaction is :


7
Products A and B formed in the following reactions are respectively :


8
If 50% of a reaction occurs in 100 second and 75% of the reaction occurs in 200 secod, the order of this reaction is :
9
For which of the following processes, $$\Delta $$S is negative ?
10
When 9.65 ampere current was passed for 1.0 hour into nitrobenzene in acidic medium, the amount of p-aminophenol produced is :
11
An unknown chlorohydrocarbon has 3.55% of chlorine. If each molecule of the hydrocarbon has one chlorine atom only; chlorine atoms present in 1 g of chlorohydrocarbon are :
(Atomic wt. of Cl = 35.5 u; Avogadro constant = 6.023 $$ \times $$ 1023 mol-1)
(Atomic wt. of Cl = 35.5 u; Avogadro constant = 6.023 $$ \times $$ 1023 mol-1)
12
The gas phase reaction 2NO2(g) $$ \to $$ N2O4(g) is an exothermic reaction. The decomposition of N2O4, in equilibrium mixture of NO2(g) and N2O4(g), can be increased by :
13
Which of the following compounds will most readily be dehydrated to give alkene under acidic condition ?
14
The incorrect geometry is represented by :
15
Among the following, the incorrect statement is :
16
For standardizing NaOH solution, which of the following is used as a primary standard ?
17
When XO2 is fused with an alkali metal hydroxide in presence of an oxidizing agent such as KNO3 ; a dark green product is formed which disproportioates in acidic solution to afforda dark purple solution. X is :
18
Which of the following conversions involves change in both shape and hybridisation ?
19
Which of the following complexes will shows geometrical isomerism ?
20
In Wilkinson's catalyst, the hybridization of central metal ion and its shape are respectively :
21
The mass of a non-volatile, non-electrolyte solute (molar mass = 50 g mol-1 ) needed to be dissolved in 114 g octane to reduce its vapour pressure to 75%, is :
22
The incorrect statement is :
23
At 320 K, a gas A2 is 20% dissociated to A(g). The standard free energy change at 320 K and 1 atm in J mol-1 is approximately : (R = 8.314 JK-1 mol-1; ln2 = 0.693; ln 3 = 1.098)
24
Which of the following statements is false ?
Mathematics
1
Let A = $$\left[ {\matrix{
1 & 0 & 0 \cr
1 & 1 & 0 \cr
1 & 1 & 1 \cr
} } \right]$$ and B = A20. Then the sum of the elements of the first column of B is :
2
If $$f(x) = \int\limits_0^x {t\left( {\sin x - \sin t} \right)dt\,\,\,} $$ then :
3
If $$\int {{{\tan x} \over {1 + \tan x + {{\tan }^2}x}}dx = x - {K \over {\sqrt A }}{{\tan }^{ - 1}}} $$ $$\left( {{{K\,\tan x + 1} \over {\sqrt A }}} \right) + C,(C\,\,$$ is a constant of integration) then the ordered pair (K, A) is equal to :
4
If $$x = \sqrt {{2^{\cos e{c^{ - 1}}}}} $$ and $$y = \sqrt {{2^{se{c^{ - 1}}t}}} \,\,\left( {\left| t \right| \ge 1} \right),$$ then $${{dy} \over {dx}}$$ is equal to :
5
If the function f defined as
$$f\left( x \right) = {1 \over x} - {{k - 1} \over {{e^{2x}} - 1}},x \ne 0,$$ is continuous at
x = 0, then the ordered pair (k, f(0)) is equal to :
$$f\left( x \right) = {1 \over x} - {{k - 1} \over {{e^{2x}} - 1}},x \ne 0,$$ is continuous at
x = 0, then the ordered pair (k, f(0)) is equal to :
6
Let M and m be respectively the absolute maximum and the absolute minimum values of the function, f(x) = 2x3 $$-$$ 9x2 + 12x + 5 in the interval [0, 3]. Then M $$-$$m is equal to :
7
Let $${1 \over {{x_1}}},{1 \over {{x_2}}},...,{1 \over {{x_n}}}\,\,$$ (xi $$ \ne $$ 0 for i = 1, 2, ..., n) be in A.P. such that x1=4 and x21 = 20. If n is the least positive integer for which $${x_n} > 50,$$ then $$\sum\limits_{i = 1}^n {\left( {{1 \over {{x_i}}}} \right)} $$ is equal to :
8
$$\mathop {\lim }\limits_{x \to 0} \,\,{{{{\left( {27 + x} \right)}^{{1 \over 3}}} - 3} \over {9 - {{\left( {27 + x} \right)}^{{2 \over 3}}}}}$$ equals.
9
The number of numbers between 2,000 and 5,000 that can be formed with the digits 0, 1, 2, 3, 4 (repetition of digits is not allowed) and are multiple of 3 is :
10
The number of values of k for which the system of linear equations,
(k + 2)x + 10y = k
kx + (k +3)y = k -1
has no solution, is :
(k + 2)x + 10y = k
kx + (k +3)y = k -1
has no solution, is :
11
If the area of the region bounded by the curves, $$y = {x^2},y = {1 \over x}$$ and the lines y = 0 and x= t (t >1) is 1 sq. unit, then t is equal to :
12
Let N denote the set of all natural numbers. Define two binary relations on N as R = {(x, y) $$ \in $$ N $$ \times $$ N : 2x + y = 10} and R2 = {(x, y) $$ \in $$ N $$ \times $$ N : x + 2y = 10}. Then :
13
Let p, q and r be real numbers (p $$ \ne $$ q, r $$ \ne $$ 0), such that the roots of the equation $${1 \over {x + p}} + {1 \over {x + q}} = {1 \over r}$$ are equal in magnitude but opposite in sign, then the sum of squares of these roots is equal to :
14
The least positive integer n for which $${\left( {{{1 + i\sqrt 3 } \over {1 - i\sqrt 3 }}} \right)^n} = 1,$$ is :
15
Two different families A and B are blessed with equal numbe of children. There are 3 tickets to be distributed amongst the children of these families so that no child gets more than one ticket. If the probability that all the tickets go to the children of the family B is $${1 \over {12}},$$ then the number of children in each family is :
16
If an angle A of a $$\Delta $$ABC satiesfies 5 cosA + 3 = 0, then the roots of the quadratic equation, 9x2 + 27x + 20 = 0 are :
17
The mean and the standard deviation(s.d.) of five observations are9 and 0, respectively. If one of the observations is changed such that the mean of the new set of five observations becomes 10, then their s.d. is :
18
Let A, B and C be three events, which are pair-wise independent and $$\overrightarrow E $$ denotes the completement of an event E. If $$P\left( {A \cap B \cap C} \right) = 0$$ and $$P\left( C \right) > 0,$$ then $$P\left[ {\left( {\overline A \cap \overline B } \right)\left| C \right.} \right]$$ is equal to :
19
Let $$\overrightarrow a = \widehat i + \widehat j + \widehat k,\overrightarrow c = \widehat j - \widehat k$$ and a vector $$\overrightarrow b $$ be such that $$\overrightarrow a \times \overrightarrow b = \overrightarrow c $$ and $$\overrightarrow a .\overrightarrow b = 3.$$ Then $$\left| {\overrightarrow b } \right|$$ equals :
20
If the angle between the lines, $${x \over 2} = {y \over 2} = {z \over 1}$$
and $${{5 - x} \over { - 2}} = {{7y - 14} \over p} = {{z - 3} \over 4}\,\,$$ is $${\cos ^{ - 1}}\left( {{2 \over 3}} \right),$$ then p is equal to :
and $${{5 - x} \over { - 2}} = {{7y - 14} \over p} = {{z - 3} \over 4}\,\,$$ is $${\cos ^{ - 1}}\left( {{2 \over 3}} \right),$$ then p is equal to :
21
If the length of the latus rectum of an ellipse is 4 units and the distance between a focus an its nearest vertex on the major axis is $${3 \over 2}$$ units, then its eccentricity is :
22
If a circle C, whose radius is 3, touches externally the circle,
$${x^2} + {y^2} + 2x - 4y - 4 = 0$$ at the point (2, 2), then the length of the intercept cut by this circle C, on the x-axis is equal to :
$${x^2} + {y^2} + 2x - 4y - 4 = 0$$ at the point (2, 2), then the length of the intercept cut by this circle C, on the x-axis is equal to :
23
The locus of the point of intersection of the lines, $$\sqrt 2 x - y + 4\sqrt 2 k = 0$$ and $$\sqrt 2 k\,x + k\,y - 4\sqrt 2 = 0$$ (k is any non-zero real parameter), is :
Physics
1
A galvanometer with its coil resistance 25 $$\Omega $$ requires a current of 1 mA for its full deflection. In order to construct an ammeter to read upto a current of 2 A, the approximate value of the shunt resistance should be :
2
Both the nucleus and the atom of some element arein their respective first excited states. They get de-excted by emitting photons of wavelengths $$\lambda $$N, $$\lambda $$A respectively. The ratio $${{{}^\lambda N} \over {{}^\lambda A}}$$is closest to :
3
The de-Broglie wavelength ($$\lambda $$B) associated with the electron orbiting in the second excited state of hydrogen atom is related to that in the ground state ($$\lambda $$G) by :
4
Unpolarized light of intensity I is incident on a system of two polarizers, A followed by B. The intensity of emergent light is I/2. If a third polarizer C is placed between A and B, the intensity of emergent light is reduced to I/3. The angle between the polarizers A and C is $$\theta $$. Then :
5
A ray of light is incident at an angle of 60o on one face of a prism of angle 30o. The emergent ray of light makes an angle of 30o with incident ray. The angle made by the emergent ray with second face of prism will be :
6
A charge q is spread uniformly over an insulated loop of radius r. If it is rotated with an angular velocity $$\omega $$ with resect to normal axis then the magnetic moment of the loop is :
7
A coil of cross-sectional area A having n turns is placed in a uniform magnetic field B. When it is rotated with an angular velocity $$\omega ,$$ the maxium e.m.f. induced in the coil will be:
8
A plane electromagnetic wave of wavelength $$\lambda $$ has an intensity I. It is propagatting along the positive Y-direction. The allowed expressions for the electric and magnetic fields are givn by :
9
A power transmission line feeds input power at 2300 V to a step down transformer with its primary windings having 4000 turns, giving the output power at 230 V. If the current in the primary of the transformer is 5 A, and its efficiency is 90%, the output current would be ;
10
Two identical conducting spheres A and B, carry equal charge. They are separated by a distance much larger than their diameters, and the force between theis F. A third identical conducting sphere, C, is uncharged. Sphere C is first touhed to A, then to B, and then removed. As a result, the force between A and B would be equal to :
11
A heating element has a resistance of 100 $$\Omega $$ at room temperature. When it is connected to a supply of 220 V, a steady current of 2 A passes in it and temperature is 500oC more than room temperature. what is the temperature coefficient of resistance of the heating element ?
12
The end correction of a resonance column is 1 cm. If the shortest length resonating with the tunning fork is 10 cm, the next resonating length should be :
13
Two moles of helium are mixed with n moles of hydrogen. If $${{Cp} \over {Cv}} = {3 \over 2}$$ for the mixture, then the value of n is :
14
A particle executes simple harmonic motion and is located at x = a, b and c at times t0, 2t0 and 3t0 respectively. The freqquency of the oscillation is :
15
A small soap bubble of radius 4 cm is trapped inside another bubble of radius 6 cm without any contact. Let P2 be the pressure inside the inner bubble and P0, the pressure outside the outer bubble. Radius of another bubble with pressure difference P2 $$-$$ P0 between its inside and outside would be :
16
An oscillator of mass M is at rest in its equilibrium position in a potential
V = $${1 \over 2}$$ k(x $$-$$ X)2. A particle of mass m comes from right with speed u and collides completely inelastically with M and sticks to it. This process repeats every time the oscillator crosses its equilibrium position. The amplitude of oscillations after 13 collisions is : (M = 10, m = 5, u = 1, k = 1)
V = $${1 \over 2}$$ k(x $$-$$ X)2. A particle of mass m comes from right with speed u and collides completely inelastically with M and sticks to it. This process repeats every time the oscillator crosses its equilibrium position. The amplitude of oscillations after 13 collisions is : (M = 10, m = 5, u = 1, k = 1)
17
The relative uncertainly in the period of a satellite orbiting around the earth is 10-2. If the relative uncertainty in the radius of the orbit is negligible, the relative uncertainty in the mass of the earth is :
18
Suppose that the angular velocity of rotation of earth is increased. Then, as a consequence :
19
Two particles of the same mass m are moving in circular orbits because of force, given by $$F\left( r \right) = {{ - 16} \over r} - {r^3}$$
The first particle is at a distance r = 1, and the second, at r = 4. The best estimate for the ratio of kinetic energies of the first and the second particle is closest to :
The first particle is at a distance r = 1, and the second, at r = 4. The best estimate for the ratio of kinetic energies of the first and the second particle is closest to :
20
A body of mass m starts moving from rest along x-axis so that its velocity varies as $$\upsilon = a\sqrt s $$ where a is a constant and s is the distance covered by the body. The total work done by all the forces acting on the body in the first t seconds after the start of the motion is :
21
Let $$\overrightarrow A $$ = $$\left( {\widehat i + \widehat j} \right)$$ and, $$\overrightarrow B = \left( {2\widehat i - \widehat j} \right).$$ The magnitude of a coplanar vector $$\overrightarrow C $$ such that $$\overrightarrow A .\overrightarrow C = \overrightarrow B .\overrightarrow C = \overrightarrow A .\overrightarrow B ,$$ is given by :
22
The percentage errors in quantities P, Q, R and S are 0.5%, 1%, 3% and 1.5% respectively in the measurement of a physical quantity A = $${{{P^3}{Q^2}} \over {\sqrt R S}}.$$
The maximum percentage error in the value of A will be :
The maximum percentage error in the value of A will be :
23
One mole of an ideal monoatomic gas is taken along the path ABCA as show in the PV diagram. The maximum temperature attained by the gas along the path BC is given by :


24
In the following circuit, the switch S is closed at t = 0. The charge on the capacitor C1 as a function of time will be given by $$\left( {{C_{eq}} = {{{C_1}{C_2}} \over {{C_1} + {C_2}}}} \right)$$


25
A thin circular disk is in the xy plane as shown in the figure. The ratio of its moment of inertia about z and z' axes will be :
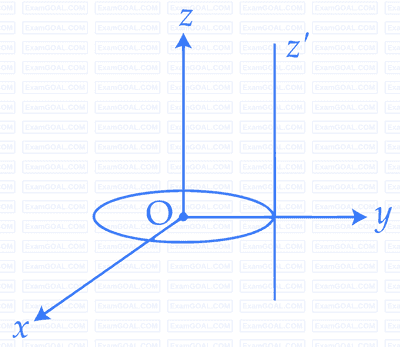

26
In the given circuit, the current through zener diode is :


27
In a circuit for finding the resistance of a galvanometer by half deflection method, a 6 V battery and a high resistance of 11 k$$\Omega $$ are used. The figure of merit of the galvanometer is 60 $$\mu A/$$division. In the absence of shunt resistance, the galvanometer produces a deflection of $$\theta $$ = 9 divisions when current flows in the circuit. The value of the shunt resistance that can cause the deflection of $$\theta /2,$$ is closest to :