JEE Main 2019 (Online) 11th January Evening Slot
Paper was held on
Fri, Jan 11, 2019 9:30 AM
Chemistry
1
Which of the following compounds will produce a precipitate with AgNO3 ?
2
In the following compound,
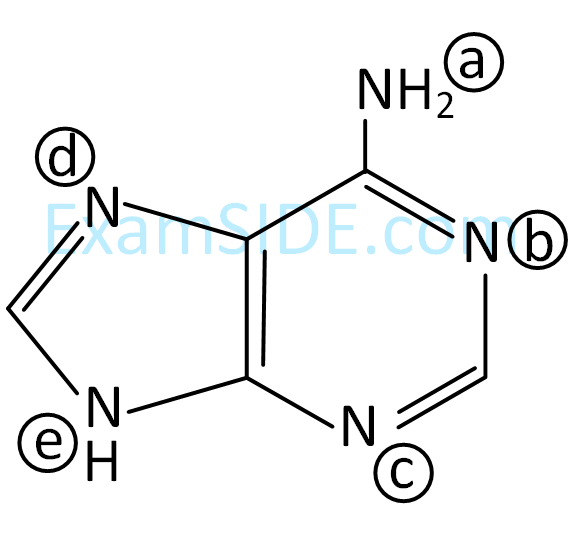
the favourable site/s for protonation is/are :

the favourable site/s for protonation is/are :
3
The major product obtained in the following conversion is


4
Which of the following compounds reacts with ethylmagnesium bromide and also decolourizes bromine water solution:
5
The major product of the following reaction is :
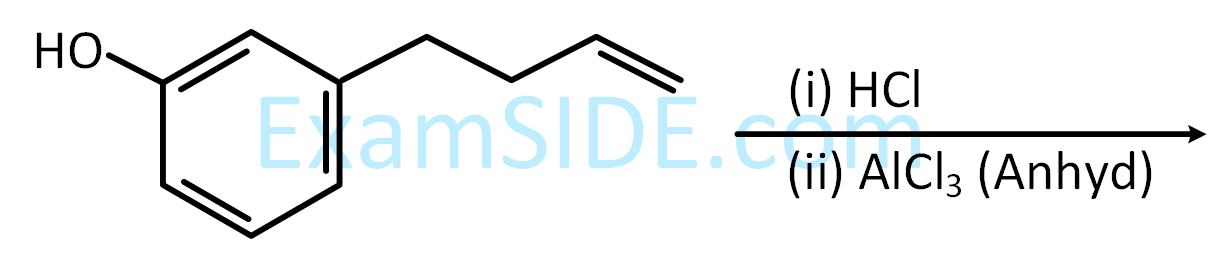

6
The major product obtained in the following reaction is :
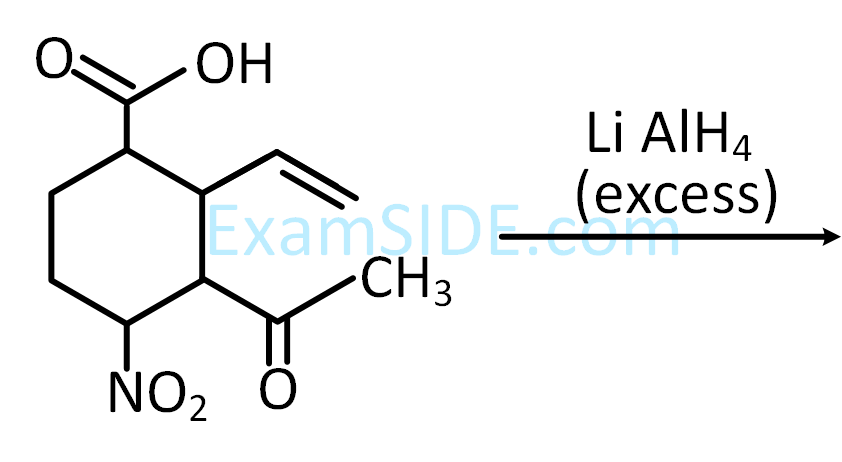

7
The coordination number of Th in K4[Th(C2O4)4(OH2)2] is :
(C2O$${_4^{2 - }}$$ = Oxalato)
(C2O$${_4^{2 - }}$$ = Oxalato)
8
The correct match between Item I and Item II is :
| Item I | Item II | ||
|---|---|---|---|
| (A) | Ester test | (P) | Tyr |
| (B) | Carbylamine test | (Q) | Asp |
| (C) | Phthalein dye test |
(R) | Ser |
| (S) | Lys | ||
9
For the equilibrium,
2H2O $$\rightleftharpoons$$ H3O+ + OH$$-$$, the value of $$\Delta $$Go at 298 K is approximately :
2H2O $$\rightleftharpoons$$ H3O+ + OH$$-$$, the value of $$\Delta $$Go at 298 K is approximately :
10
25 ml of the given HCl solution requires 30 mL of 0.1 M sodium carbonate solution. What is the volume of this HCl solution required to titrate 30 mL of 0.2 M aqueous NaOH solutions ?
11
Given the equilibrium constant:
KC of the reaction :
Cu(s) + 2Ag+ (aq) $$ \to $$ Cu2+ (aq) + 2Ag(s) is
10 $$ \times $$ 1015, calculate the E$$_{cell}^0$$ of this reaciton at 298 K
[2.303 $${{RT} \over F}$$ at 298 K = 0.059V]
KC of the reaction :
Cu(s) + 2Ag+ (aq) $$ \to $$ Cu2+ (aq) + 2Ag(s) is
10 $$ \times $$ 1015, calculate the E$$_{cell}^0$$ of this reaciton at 298 K
[2.303 $${{RT} \over F}$$ at 298 K = 0.059V]
12
The number of bridging CO ligand(s) and Co-Co bond(s) in Co2(CO)8, respectively are :
13
The reaction 2X $$ \to $$ B is a zeroth order reaction. If the initial concentration of X is 0.2 M, the half-life is 6 h. When the initial concentration of X is 0.5 M, the time required to reach its final concentration of 0.2 M will
be:
14
A compound 'X' on treatment with Br2/NaOH, provided C3H9N, which gives positive carbylamine test. Compound 'X' is :
15
The standard reaction Gibbs energy for a chemical reaction at an absolute temperature T is given by
$$\Delta $$rGo = A – BT
Where A and B are non-zero constants. Which of the following is TRUE about this reaction?
Where A and B are non-zero constants. Which of the following is TRUE about this reaction?
16
$$\underline A \,\,\buildrel {4KOH,{O_2}} \over
\longrightarrow \,\,\mathop {2\underline B }\limits_{\left( {Green} \right)} \,\, + \,\,2{H_2}O$$
$$3\underline B \,\,\buildrel {4HCl} \over \longrightarrow \,\,\mathop {2\underline C }\limits_{\left( {Purple} \right)} \,\, + \,\,Mn{O_2} + 2{H_2}O$$
$$2\underline C \,\,\buildrel {{H_2}O.KI} \over \longrightarrow \,\,\mathop {2\underline A }\limits_{\left( {Purple} \right)} \,\, + \,\,2KOH\,\, + \,\,\underline D $$
In the above sequence of reactions, $${\underline A }$$ and $${\underline D }$$, respectively, are :
$$3\underline B \,\,\buildrel {4HCl} \over \longrightarrow \,\,\mathop {2\underline C }\limits_{\left( {Purple} \right)} \,\, + \,\,Mn{O_2} + 2{H_2}O$$
$$2\underline C \,\,\buildrel {{H_2}O.KI} \over \longrightarrow \,\,\mathop {2\underline A }\limits_{\left( {Purple} \right)} \,\, + \,\,2KOH\,\, + \,\,\underline D $$
In the above sequence of reactions, $${\underline A }$$ and $${\underline D }$$, respectively, are :
17
The reaction, MgO(s) + C(s) $$ \to $$ Mg(s) + CO(g), for which $$\Delta $$rHo + 491.1 kJ mol–1 and $$\Delta $$rSo = 198.0 JK–1 mol–1, is not feasible at 298 K. Temperature above which reaciton will be feasible is :
18
The de Broglie wavelength ($$\lambda $$) associated with a photoelectron varies with the frequency (v) of the incident radiation as, [v0 is threshold frequency] :
19
K2Hgl4 is 40% ionised in aqueous solution. The value of its van't Hoff factor (i) is:
20
The correct option with respect to the Pauling electronegativity values of the element is :
Mathematics
1
Let x, y be positive real numbers and m, n positive integers. The maximum value of the expression $${{{x^m}{y^n}} \over {\left( {1 + {x^{2m}}} \right)\left( {1 + {y^{2n}}} \right)}}$$ is :
2
If a hyperbola has length of its conjugate axis equal to 5 and the distance between its foci is 13, then the
eccentricity of the hyperbola is :
3
Let S = {1, 2, . . . . . ., 20}. A subset B of S is said to be "nice", if the sum of the elements of B is 203. Then the probability that a randonly chosen subset of S is "nice" is :
4
Let the length of the latus rectum of an ellipse with its major axis along x-axis and centre at the origin, be 8. If the distance between the foci of this ellipse is equal to the length of its minor axis, then which one of the following points lies on it?
5
Let f(x) = $${x \over {\sqrt {{a^2} + {x^2}} }} - {{d - x} \over {\sqrt {{b^2} + {{\left( {d - x} \right)}^2}} }},\,\,$$ x $$\, \in $$ R, where a, b and d are non-zero real constants. Then :
6
The integral $$\int\limits_{\pi /6}^{\pi /4} {{{dx} \over {\sin 2x\left( {{{\tan }^5}x + {{\cot }^5}x} \right)}}} $$ equals :
7
Let a function f : (0, $$\infty $$) $$ \to $$ (0, $$\infty $$) be defined by f(x) = $$\left| {1 - {1 \over x}} \right|$$. Then f is :
8
If $$\int {{{x + 1} \over {\sqrt {2x - 1} }}} \,dx$$ = f(x) $$\sqrt {2x - 1} $$ + C, where C is a constant of integration, then f(x) is equal to :
9
The area (in sq. units) in the first quadrant bounded by the parabola, y = x2 + 1, the tangent to it at the point (2, 5) and the coordinate axes is :
10
$$\mathop {\lim }\limits_{x \to 0} {{x\cot \left( {4x} \right)} \over {{{\sin }^2}x{{\cot }^2}\left( {2x} \right)}}$$ is equal to :
11
Let $$\alpha $$ and $$\beta $$ be the roots of the quadratic equation x2
sin $$\theta $$ – x(sin $$\theta $$ cos $$\theta $$ + 1) + cos $$\theta $$ = 0 (0 < $$\theta $$ < 45o), and $$\alpha $$ < $$\beta $$. Then $$\sum\limits_{n = 0}^\infty {\left( {{\alpha ^n} + {{{{\left( { - 1} \right)}^n}} \over {{\beta ^n}}}} \right)} $$ is equal to :
12
If $$\left| {\matrix{
{a - b - c} & {2a} & {2a} \cr
{2b} & {b - c - a} & {2b} \cr
{2c} & {2c} & {c - a - b} \cr
} } \right|$$
= (a + b + c) (x + a + b + c)2, x $$ \ne $$ 0,
then x is equal to :
= (a + b + c) (x + a + b + c)2, x $$ \ne $$ 0,
then x is equal to :
13
If 19th term of a non-zero A.P. is zero, then its (49th term) : (29th term) is :
14
Let z be a complex number such that |z| + z = 3 + i (where i = $$\sqrt { - 1} $$). Then |z| is equal to :
15
Let K be the set of all real values of x where the function f(x) = sin |x| – |x| + 2(x – $$\pi $$) cos |x| is not differentiable. Then the set K is equal to :
16
The number of functions f from {1, 2, 3, ...., 20} onto {1, 2, 3, ...., 20} such that f(k) is a multiple of 3,
whenever k is a multiple of 4, is :
17
The solution of the differential equation,
$${{dy} \over {dx}}$$ = (x – y)2, when y(1) = 1, is :
$${{dy} \over {dx}}$$ = (x – y)2, when y(1) = 1, is :
18
A circle cuts a chord of length 4a on the x-axis and passes through a point on the y-axis, distant 2b from the origin. Then the locus of the centre of this circle, is :
19
If the area of the triangle whose one vertex is at the vertex of the parabola, y2 + 4(x – a2) = 0 and the othertwo vertices are the points of intersection of the parabola and y-axis, is 250 sq. units, then a value of 'a' is :
20
If in a parallelogram ABDC, the coordinates of A, B and C are respectively (1, 2), (3, 4) and (2, 5), then the
equation of the diagonal AD is :
21
All x satisfying the inequality (cot–1
x)2– 7(cot–1 x) + 10 > 0, lie in the interval :
22
Let $$\sqrt 3 \widehat i + \widehat j,$$ $$\widehat i + \sqrt 3 \widehat j$$ and $$\beta \widehat i + \left( {1 - \beta } \right)\widehat j$$ respectively be the position vectors of the points A, B and C with respect to the origin O. If the distance of C from the bisector of the acute angle between OA and OB is $${3 \over {\sqrt 2 }}$$, then the sum of all possible values of $$\beta $$ is :
Physics
1
A string is wound around a hollow cylinder of mass 5 kg and radius 0.5m. If the string is now pulled with a horizontal force of 40 N, and the cylinder is rolling without slipping on a horizontal surface (see figure), then the angular acceleration of the cylinder will be (Neglect the mass and thickness of the string) :
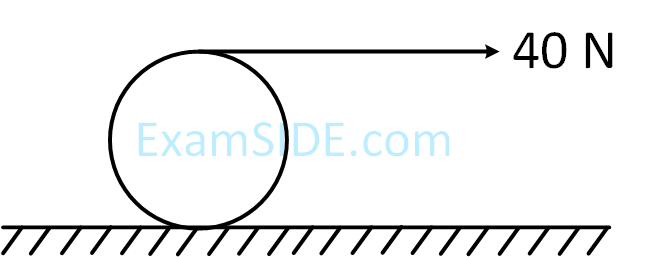

2
In the experimental set up of metre bridge shown in the figure, the null point is obtained at a distance of 40 cm from A. If a 10 $$\Omega $$ resistor is connected in series with R1, the null point shifts by 10 cm. The resistance that should be connected in parallel with (R1 + 10) $$\Omega $$ such that the null point shifts back to its initial position is :
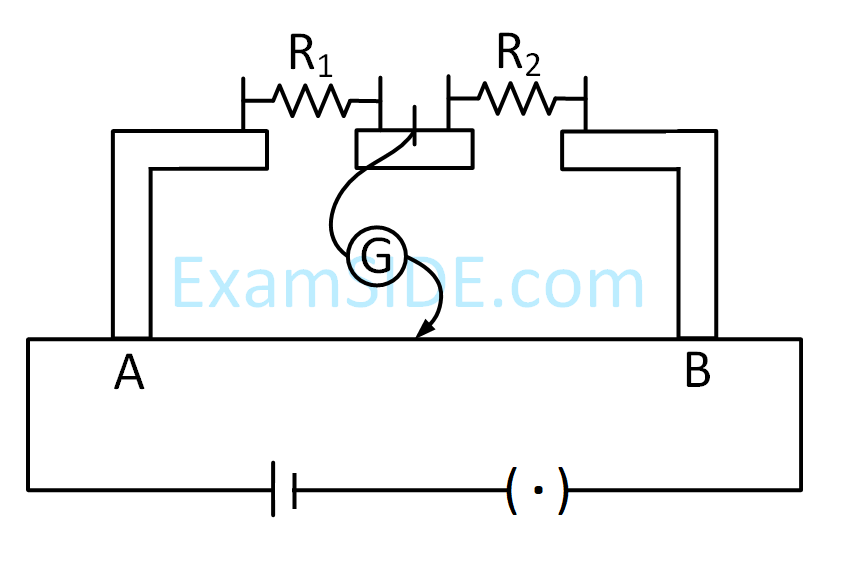

3
The circuit shown below contains two ideal diodes, each with a forward resistance of 50 $$\Omega $$. If the battery voltage is 6 V, the current through the 100 $$\Omega $$ resistance (in Amperes) is :


4
Seven capacitors, each of capacitance 2 $$\mu $$F, are to be connected in a configuration to obtain an effective capacitance of $$\left( {{6 \over {13}}} \right)\mu F.$$ Which of the combinations, shown in figures below, will achieve the desired value
5
In the circuit shown, the potential difference between A and B is :
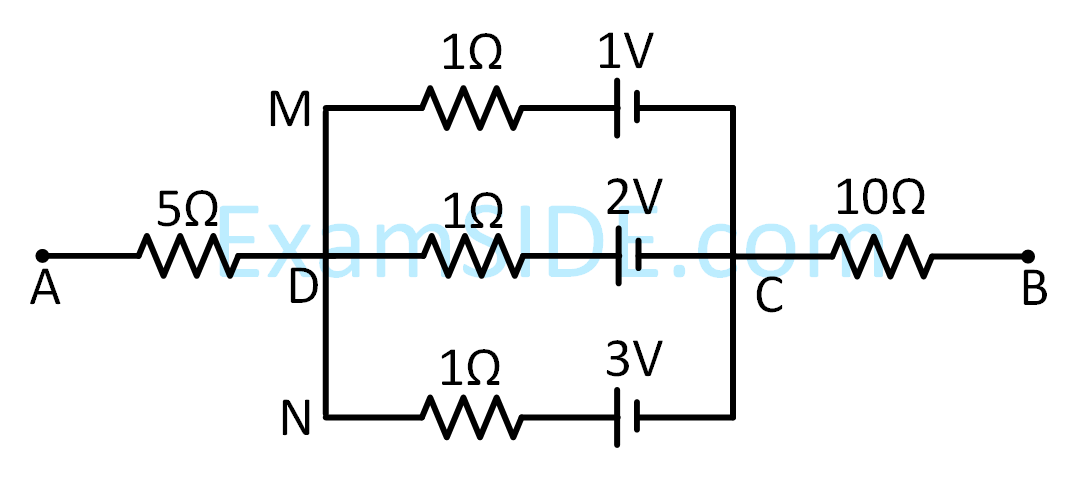

6
A circular disc D1 of mass M and radius R has two identical discs D2 and D3 of the same mass M and radius R attached rigidly at its opposite ends (see figure). The moment of inertia of the system about the axis OO' ,passing through the centre of D1 as shown in the figure, will be :
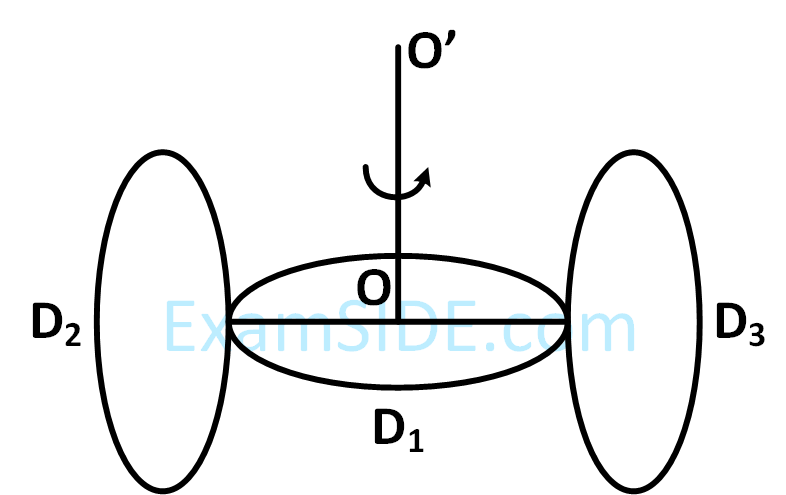

7
A pendulum is executing simple harmonic motion and its maximum kinetic energy is K1. If the length of the pendulum is doubled and it performs simple harmonic motion with the same amplitude as in the first case, its maximum kinetic energy is K2. Then :
8
A particle moves from the point $$\left( {2.0\widehat i + 4.0\widehat j} \right)$$ m, at t = 0, with an initial velocity $$\left( {5.0\widehat i + 4.0\widehat j} \right)$$ ms$$-$$1. It is acted upon by a constant force which produces a constant acceleration $$\left( {4.0\widehat i + 4.0\widehat j} \right)$$ ms$$-$$2. What is the distance of the particle from the origin at time 2 s?
9
The magnitude of torque on a particle of mass 1 kg is 2.5 Nm about the origin. If the force acting on it is 1 N, and the distance of the particle from the origin is 5m, the angle between the force and the position vector is (in radians) :
10
A copper wire is wound on a wooden frame, whose shape is that of an equilateral triangle. If the linear
dimension of each side of the frame is increased by a factor of 3, keeping the number of turns of the coil per
unit length of the frame the same, then the self inductance of the coil:
11
If speed (V), acceleration (A) and force (F) are considered as fundamental units, the dimension of Young,s modulus will be:
12
A particle of mass m and charge q is in an electric and magnetic field given by
$$\overrightarrow E = 2\widehat i + 3\widehat j;\,\,\,\overrightarrow B = 4\widehat j + 6\widehat k.$$
The charged particle is shifted from he origin to the point P(x = 1; y = 1) along a straight path. The magnitude of the total work done is :
$$\overrightarrow E = 2\widehat i + 3\widehat j;\,\,\,\overrightarrow B = 4\widehat j + 6\widehat k.$$
The charged particle is shifted from he origin to the point P(x = 1; y = 1) along a straight path. The magnitude of the total work done is :
13
A galvanometer having a resistance of 20 $$\Omega $$ and 30 divisions on both sides has figure of merit 0.005 ampere/division. The resistance that should be connected in series such that it can be used as a voltmeter upto 15 volt, is:
14
In a photoelectric experiment, the wavelength of the light incident on a metal is changed from 300 nm to 400 nm. The decrease in the stopping potential is close to: ($${{{hc} \over e}}$$ = 1240 nm eV)
15
A particle of mass m is moving in a straight line with momentum p. Starting at time t = 0, a force F = kt acts in the same direction on the moving particle during time interval T so that its momentum changes from p to 3p. Here k is a constant. The value of T is :
16
A 27 mW laser beam has a cross-sectional area of 10 mm2. The magnitude of the maximum electric field in this electromagnetic wave is given by :
[Given permittivity of space $$ \in $$0 = 9 $$ \times $$ 10–12 SI units, Speed of light c = 3 $$ \times $$ 108 m/s]
[Given permittivity of space $$ \in $$0 = 9 $$ \times $$ 10–12 SI units, Speed of light c = 3 $$ \times $$ 108 m/s]
17
A thermometer graduated according to a linear scale reads a value x0 when in contact with boiling water, and x0/3 when in contact with ice. What is the temperature of an object in oC, if this thermometer in the contact with the object reads x0/2 ?
18
In a hydrogen like atom, when an electron jumps from the M-shell to the L-shell, the wavelength of emitted radiation is $$\lambda $$. If an electron jumps from N-shell to the L-shell, the wavelength of emitted radiation will be:
19
The mass and the diameter of a planet are three times the respective values for the Earth. The period of oscillation of simple pendulum on the Earth is 2 s. The period of oscillation of the same pendulum on the planet would be :
20
A paramagnetic substance in the form of a cube with sides 1 cm has a magnetic dipole moment of 20 $$ \times $$ 10–6 J/ T when a magnetic intensity of 60 $$ \times $$ 103 A/m is applied. Its magnetic susceptibility is
21
A monochromatic light is incident at a certain angle on an equilateral triangular prism and suffers minimum deviation. If the refractive index of the material of the prism is $$\sqrt 3 $$, then the angle of incidence is:
22
A metal ball of mass 0.1 kg is heated upto 500oC and dropped into a vessel of heat capacity 800 JK–1 and containing 0.5 kg water. The initial temperature of water and vessel is 30oC. What is the approximate percentage increment in the temperature of the water? [Specific Heat Capacities of water and metal are, respectively, 4200 Jkg–1 and 400 Jkg–1 K–1
23
An electric field of 1000 V/m is applied to an electric dipole at angle of 45o. The value of electric dipole moment is 10–29 C.m. What is the potential energy of the electric dipole?
24
When 100 g of a liquid A at 100oC is added to 50 g of a liquid B at temperature 75oC, the temperature of the mixture becomes 90oC. The temperature of the mixture, if 100 g of liquid A at 100oC is added to 50 g of liquid B at 50oC, will be :
25
Two rods A and B of identical dimensions are at temperature 30°C. If A is heated upto 180oC and B upto ToC, then the new lengths are the same. If the ratio of the coefficients of linear expansion of A and B is 4 : 3, then the value of T is
26
In a double-slit experiment, green light (5303$$\mathop A\limits^ \circ $$) falls on a double slit having a separation of 19.44 $$\mu $$m and awidht of 4.05 $$\mu $$m. The number of bright fringes between the first and the second diffraction minima is :
27
The region between y = 0 and y = d contains a magnetic field $$\overrightarrow B = B\widehat z$$. A particle of mass m and charge q enters the region with a velocity $$\overrightarrow v = v\widehat i.$$ If d $$=$$ $${{mv} \over {2qB}},$$ the acceleration of the charged particle at the point of its emergence at the other side is :
28
In a process, temperature and volume of one mole of an ideal monoatomic gas are varied according to the relation VT = K, where K is a constant. In this process the temperature of the gas is increased by $$\Delta $$T. The
amount of heat absorbed by gas is (R is gas constant) :