AIEEE 2002
Paper was held on
Sat, Apr 27, 2002 9:30 AM
Chemistry
1
If an endothermic reaction is non-spontaneous at freezing point of water and becomes feasible at its boiling point, then :
2
For the reactions
2C + O2 $$\to$$ 2CO2; $$\Delta H$$ = -393 J
2Zn + O2 $$\to$$ 2ZnO; $$\Delta H$$ = -412 J
2C + O2 $$\to$$ 2CO2; $$\Delta H$$ = -393 J
2Zn + O2 $$\to$$ 2ZnO; $$\Delta H$$ = -412 J
3
The heat required to raise the temperature of body by 1 K is called :
4
A heat engine absorbs heat Q1 at temperature T1 and heat Q2 at temperature T2. Work done by the engine is J (Q1 + Q2). This data :
5
1 M NaCL and 1 M HCL are present in an aqueous solution. The solution is
6
Species acting as both Bronsted acid and base is :
7
Let the solubility of an aqueous solution of Mg(OH)2 be x then its Ksp is :
8
Change in volume of the system does not alter which of the following equilibria?
9
For the reaction CO (g) + (1/2) O2 (g) $$\leftrightharpoons$$ CO2 (g), Kp/Kc is :
10
Which of the following does not show geometrical isomerism?
11
A similarity between optical and geometrical isomerism is that
12
The functional group, which is found in amino acid is
13
Arrangement of (CH3)3C-, (CH3)2CH-, CH3-CH2- when attached to benzyl or an unsaturated group in increasing order of inductive effect is
14
Racemic mixture is formed by mixing two
15
The reaction :
$${(CH)_3}C - Br\buildrel {{H_2}O} \over \longrightarrow {(CH)_3}C - OH$$
$${(CH)_3}C - Br\buildrel {{H_2}O} \over \longrightarrow {(CH)_3}C - OH$$
16
In which of the following species is the underlined carbon having sp3 hybridisation?
17
What is the product when acetylene reacts with hypochlorous acid ?
18
Which of these will not react with acetylene ?
19
In a mixture of A and B, components show negative deviation when :
20
Freezing point of an aqueous solution is (-0.186)oC. Elevation of boiling point of the same solution is Kb = 0.512 oC, Kf = 1.86 oC, find the increase in boiling point.
21
RNA is different from DNA because RNA contains
22
How do we differentiate between Fe3+ and Cr3+ in group III?
23
When primary amine reacts with chloroform in ethanoic KOH then the product is
24
Which of the following compounds has wrong $$IUPAC$$ name ?
25
Following types of compounds (as $$I, II$$ )

are studied in terms of isomerism in :

are studied in terms of isomerism in :
26
The correct order of ionic radius is
27
$$C{e^{ + 3}},\,\,L{a^{ + 3}},\,\,P{m^{ + 3}}\,\,$$ and $$Y{b^{ + 3}}\,\,$$ have ionic radial in the increasing order as
28

29
Picric acid is :
30
The type isomerism present in nitropentammine chromium $$\left( {{\rm I}{\rm I}{\rm I}} \right)$$ chloride is :
31
Conductivity (Seimen’s S) is directly proportional to area of the vessel and the concentration
of the solution in it and is inversely proportional to the length of the vessel then, then constant of proportionality is expressed in :
32
For the following cell with hydrogen electrodes at two different pressure p1 and p2. What will be the emf for the given cell :
$$\eqalign{ & Pt({H_2})|{H^ + }(aq)|Pt({H_2}) \cr & \,\,\,\,\,{p_1}\,\,\,\,\,\,\,\,\,\,\,\,\,\,1M\,\,\,\,\,\,\,\,\,\,\,\,{p_2} \cr} $$
$$\eqalign{ & Pt({H_2})|{H^ + }(aq)|Pt({H_2}) \cr & \,\,\,\,\,{p_1}\,\,\,\,\,\,\,\,\,\,\,\,\,\,1M\,\,\,\,\,\,\,\,\,\,\,\,{p_2} \cr} $$
33
EMF of a cell in terms of reduction potential of its left and right electrodes is :
34
Which of the following reaction is possible at anode?
35
When the sample of copper with zinc impurity is to be purified by electrolysis, the appropriate
electrodes are :
36
Which of the following is a redox reaction ?
37
Units of rate constant of first and zero order reactions in terms of molarity M unit are respectively
38
For the reaction A + 2B $$\to$$ C, rate is given by R = [A] [B]2 then the order of the reaction is
39
The differential rate law for the reaction H2 + I2 $$\to$$ 2HI is
40
If half-life of a substance is 5 yrs, then the total amount of substance left after 15 years, when initial amount is 64 grams is
41
The integrated rate equation is Rt = log C0 - log Ct . The straight line graph is obtained by
plotting
42
$$\beta$$ - particle is emitted in radioactivity by
43
Which of the following statements is true?
44
Oxidation number of Cl in CaOCl2 (bleaching powder) is :
45
When KMnO4 acts as an oxidising agent and ultimately forms [MnO4]-2, MnO2, Mn2O3, Mn+2
then the number of electrons transferred in each case respectively is :
46
Most common oxidation states of Ce (cerium) are :
47
Which of the following ions has the maximum magnetic moment?
48
A square planar complex is formed by hybridisation of which atomic orbitals ?
49
The most stable ion is :
50
CH3 - Mg - Br is an organometallic compound due to :
51

What is B?
52
With increase of temperature, which of these changes?
53
In a compound C, H and N atoms are present in 9 : 1 : 3.5 by weight . Molecular weight of the compound is 108 g mol-1 . Molecular formula of compound is
54
Number of atoms in 558.5 gram Fe (at. wt. of Fe = 55.85 g mol-1) is
55
In a hydrogen atom, if energy of an electron in ground state is -13.6 eV, then that in the 2nd excited state is
56
Uncertainty in position of a minute particle of mass 25 g in space is 10-5 m. What is the uncertainty in its velocity (in ms-1) (h = 6.6 $$\times$$ 10-34 Js)
57
In which of the following species the interatomic bond angle is 109o28' ?
58
Hybridisation of underline atom changes in
59
Which of the following are arranged in an increasing order of their bond strengths?
60
Acetylene does not react with :
61
For a cell given below

$$ \begin{aligned} \mathrm{Ag}^{+}+\mathrm{e}^{-} & \longrightarrow \mathrm{Ag}; E^{\circ}=x \\\\ \mathrm{Cu}^{2+}+2 e^{-} & \longrightarrow \mathrm{Cu}{;} E^{\circ}=y \end{aligned} $$
$$ E^{\circ} \text { cell is } $$ :

$$ \begin{aligned} \mathrm{Ag}^{+}+\mathrm{e}^{-} & \longrightarrow \mathrm{Ag}; E^{\circ}=x \\\\ \mathrm{Cu}^{2+}+2 e^{-} & \longrightarrow \mathrm{Cu}{;} E^{\circ}=y \end{aligned} $$
$$ E^{\circ} \text { cell is } $$ :
Mathematics
1
f(x) and g(x) are two differentiable functions on [0, 2] such that
f''(x) - g''(x) = 0, f'(1) = 2, g'(1) = 4, f(2) = 3, g(2) = 9
then f(x) - g(x) at x = $${3 \over 2}$$ is
f''(x) - g''(x) = 0, f'(1) = 2, g'(1) = 4, f(2) = 3, g(2) = 9
then f(x) - g(x) at x = $${3 \over 2}$$ is
2
In a class of 100 students there are 70 boys whose average marks in a subject are 75. If the average marks of the complete class is 72, then what is the average marks of the girls?
3
$$\mathop {\lim }\limits_{x \to 0} {{\sqrt {1 - \cos 2x} } \over {\sqrt 2 x}}$$ is
4
The domain of $${\sin ^{ - 1}}\left[ {{{\log }_3}\left( {{x \over 3}} \right)} \right]$$ is
5
$$\mathop {\lim }\limits_{x \to \infty } {\left( {{{{x^2} + 5x + 3} \over {{x^2} + x + 2}}} \right)^x}$$
6
Let $$f(2) = 4$$ and $$f'(x) = 4.$$
Then $$\mathop {\lim }\limits_{x \to 2} {{xf\left( 2 \right) - 2f\left( x \right)} \over {x - 2}}$$ is given by
Then $$\mathop {\lim }\limits_{x \to 2} {{xf\left( 2 \right) - 2f\left( x \right)} \over {x - 2}}$$ is given by
7
$$\mathop {\lim }\limits_{x \to 0} {{\log {x^n} - \left[ x \right]} \over {\left[ x \right]}}$$, $$n \in N$$, ( [x] denotes the greatest integer less than or equal to x )
8
If $$f\left( 1 \right) = 1,{f'}\left( 1 \right) = 2,$$ then
$$\mathop {\lim }\limits_{x \to 1} {{\sqrt {f\left( x \right)} - 1} \over {\sqrt x - 1}}$$ is
$$\mathop {\lim }\limits_{x \to 1} {{\sqrt {f\left( x \right)} - 1} \over {\sqrt x - 1}}$$ is
9
$$f$$ is defined in $$\left[ { - 5,5} \right]$$ as
$$f\left( x \right) = x$$ if $$x$$ is rational
$$\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$ = - x$$ if $$x$$ is irrational. Then
$$f\left( x \right) = x$$ if $$x$$ is rational
$$\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$ = - x$$ if $$x$$ is irrational. Then
10
If f(x + y) = f(x).f(y) $$\forall $$ x, y and f(5) = 2, f'(0) = 3, then
f'(5) is
f'(5) is
11
A triangle with vertices $$\left( {4,0} \right),\left( { - 1, - 1} \right),\left( {3,5} \right)$$ is :
12
Locus of mid point of the portion between the axes of
$$x$$ $$cos$$ $$\alpha + y\,\sin \alpha = p$$ where $$p$$ is constant is :
$$x$$ $$cos$$ $$\alpha + y\,\sin \alpha = p$$ where $$p$$ is constant is :
13
If $$y=f(x)$$ makes +$$ve$$ intercept of $$2$$ and $$0$$ unit on $$x$$ and $$y$$ axes and encloses an area of $$3/4$$ square unit with the axes then $$\int\limits_0^2 {xf'\left( x \right)dx} $$ is
14
If $$y = {\left( {x + \sqrt {1 + {x^2}} } \right)^n},$$ then $$\left( {1 + {x^2}} \right){{{d^2}y} \over {d{x^2}}} + x{{dy} \over {dx}}$$ is
15
$${\cot ^{ - 1}}\left( {\sqrt {\cos \alpha } } \right) - {\tan ^{ - 1}}\left( {\sqrt {\cos \alpha } } \right) = x,$$ then sin x is equal to :
16
The maximum distance from origin of a point on the curve
$$x = a\sin t - b\sin \left( {{{at} \over b}} \right)$$
$$y = a\cos t - b\cos \left( {{{at} \over b}} \right),$$ both $$a,b > 0$$ is
$$x = a\sin t - b\sin \left( {{{at} \over b}} \right)$$
$$y = a\cos t - b\cos \left( {{{at} \over b}} \right),$$ both $$a,b > 0$$ is
17
If $$a>0$$ and discriminant of $$\,a{x^2} + 2bx + c$$ is $$-ve$$, then
$$\left| {\matrix{ a & b & {ax + b} \cr b & c & {bx + c} \cr {ax + b} & {bx + c} & 0 \cr } } \right|$$ is equal to
$$\left| {\matrix{ a & b & {ax + b} \cr b & c & {bx + c} \cr {ax + b} & {bx + c} & 0 \cr } } \right|$$ is equal to
18
$$\int\limits_0^{10\pi } {\left| {\sin x} \right|dx} $$ is
19
$${I_n} = \int\limits_0^{\pi /4} {{{\tan }^n}x\,dx} $$ then $$\,\mathop {\lim }\limits_{n \to \infty } \,n\left[ {{I_n} + {I_{n + 2}}} \right]$$ equals
20
$$\int\limits_0^2 {\left[ {{x^2}} \right]dx} $$ is
21
$$\int_{ - \pi }^\pi {{{2x\left( {1 + \sin x} \right)} \over {1 + {{\cos }^2}x}}} dx$$ is
22
The equation of a circle with origin as a center and passing through an equilateral triangle whose median is of length $$3$$$$a$$ is :
23
The area bounded by the curves $$y = \ln x,y = \ln \left| x \right|,y = \left| {\ln {\mkern 1mu} x} \right|$$ and $$y = \left| {\ln \left| x \right|} \right|$$ is :
24
The order and degree of the differential equation
$$\,{\left( {1 + 3{{dy} \over {dx}}} \right)^{2/3}} = 4{{{d^3}y} \over {d{x^3}}}$$ are
$$\,{\left( {1 + 3{{dy} \over {dx}}} \right)^{2/3}} = 4{{{d^3}y} \over {d{x^3}}}$$ are
25
The solution of the equation $$\,{{{d^2}y} \over {d{x^2}}} = {e^{ - 2x}}$$
26
$$A$$ and $$B$$ are events such that $$P\left( {A \cup B} \right) = 3/4$$,$$P\left( {A \cap B} \right) = 1/4,$$
$$P\left( {\overline A } \right) = 2/3$$ then $$P\left( {\overline A \cap B} \right)$$ is :
$$P\left( {\overline A } \right) = 2/3$$ then $$P\left( {\overline A \cap B} \right)$$ is :
27
A problem in mathematics is given to three students $$A,B,C$$ and their respective probability of solving the problem is $${1 \over 2},{1 \over 3}$$ and $${1 \over 4}.$$ Probability that the problem is solved is :
28
If $$\left| {\overrightarrow a } \right| = 4,\left| {\overrightarrow b } \right| = 2$$ and the angle between $${\overrightarrow a }$$ and $${\overrightarrow b }$$ is $$\pi /6$$ then $${\left( {\overrightarrow a \times \overrightarrow b } \right)^2}$$ is equal to :
29
If the vectors $\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}$ and $\overrightarrow{\mathbf{c}}$ from the sides $B C, C A$ and $A B$ respectively of a triangle $A B C$, then :
30
If $$\left| {\overrightarrow a } \right| = 5,\left| {\overrightarrow b } \right| = 4,\left| {\overrightarrow c } \right| = 3$$ thus what will be the value of $$\left| {\overrightarrow a .\overrightarrow b + \overrightarrow b .\overrightarrow c + \overrightarrow c .\overrightarrow a } \right|,$$ given that $$\overrightarrow a + \overrightarrow b + \overrightarrow c = 0$$ :
31
$$\overrightarrow a = 3\widehat i - 5\widehat j$$ and $$\overrightarrow b = 6\widehat i + 3\widehat j$$ are two vectors and $$\overrightarrow c $$ is a vector such that $$\overrightarrow c = \overrightarrow a \times \overrightarrow b $$ then $$\left| {\overrightarrow a } \right|:\left| {\overrightarrow b } \right|:\left| {\overrightarrow c } \right|$$ =
32
If the vectors $$\overrightarrow c ,\overrightarrow a = x\widehat i + y\widehat j + z\widehat k$$ and $$\widehat b = \widehat j$$ are such that $$\overrightarrow a ,\overrightarrow c $$ and $$\overrightarrow b $$ form a right handed system then $${\overrightarrow c }$$ is :
33
The period of $${\sin ^2}\theta $$ is
34
Which one is not periodic?
35
z and w are two nonzero complex numbers such that $$\,\left| z \right| = \left| w \right|$$ and Arg z + Arg w =$$\pi $$ then z equals
36
If $$\left| {z - 4} \right| < \left| {z - 2} \right|$$, its solution is given by :
37
The locus of the centre of a circle which touches the circle $$\left| {z - {z_1}} \right| = a$$ and$$\left| {z - {z_2}} \right| = b\,$$ externally
($$z,\,{z_1}\,\& \,{z_2}\,$$ are complex numbers) will be :
($$z,\,{z_1}\,\& \,{z_2}\,$$ are complex numbers) will be :
38
If $$\alpha \ne \beta $$ but $${\alpha ^2} = 5\alpha - 3$$ and $${\beta ^2} = 5\beta - 3$$ then the equation having $$\alpha /\beta $$ and $$\beta /\alpha \,\,$$ as its roots is
39
Product of real roots of equation $${t^2}{x^2} + \left| x \right| + 9 = 0$$
40
Difference between the corresponding roots of $${x^2} + ax + b = 0$$ and $${x^2} + bx + a = 0$$ is same and $$a \ne b,$$ then
41
If $$p$$ and $$q$$ are the roots of the equation $${x^2} + px + q = 0,$$ then
42
If $$a,\,b,\,c$$ are distinct $$ + ve$$ real numbers and $${a^2} + {b^2} + {c^2} = 1$$ then $$ab + bc + ca$$ is
43
The coefficients of $${x^p}$$ and $${x^q}$$ in the expansion of $${\left( {1 + x} \right)^{p + q}}$$ are
44
The positive integer just greater than $${\left( {1 + 0.0001} \right)^{10000}}$$ is
45
Total number of four digit odd numbers that can be formed using 0, 1, 2, 3, 5, 7 (using repetition allowed) are :
46
Number greater than 1000 but less than 4000 is formed using the digits 0, 1, 2, 3, 4 (repetition allowed). Their number is :
47
Five digit number divisible by 3 is formed using 0, 1, 2, 3, 4 and 5 without repetition. Total number of such numbers are :
48
The sum of integers from 1 to 100 that are divisible by 2 or 5 is :
49
If 1, $${\log _9}\,\,({3^{1 - x}} + 2),\,\,{\log _3}\,\,({4.3^x} - 1)$$ are in A.P. then x equals
50
l, m, n are the $${p^{th}}$$, $${q^{th}}$$ and $${r^{th}}$$ term of a G.P all positive, $$then\,\left| {\matrix{
{\log \,l} & p & 1 \cr
{\log \,m} & q & 1 \cr
{\log \,n} & r & 1 \cr
} } \right|\,equals$$
51
Fifth term of a GP is 2, then the product of its 9 terms is
52
Sum of infinite number of terms of GP is 20 and sum of their square is 100. The common ratio of GP is
53
If the chord y = mx + 1 of the circle $${x^2}\, + \,{y^2} = 1$$ subtends an angle of measure $${45^ \circ }$$ at the major segment of the circle then value of m is :
Physics
1
The energy band gap is maximum in
2
Which of the following are not electromagnetic waves?
3
By increasing the temperature, the specific resistance of a conductor and a semiconductor
4
If two mirrors are kept at $${60^ \circ }$$ to each other, then the number of images formed by them is
5
A wire when connected to $$220$$ $$V$$ mains supply has power dissipation $${P_1}.$$ Now the wire is cut into two equal pieces which are connected in parallel to the same supply. Power dissipation in this case is $${P_2}.$$ Then $${P_2}:{P_1}$$ is
6
If in the circuit, power dissipation is $$150W,$$ then $$R$$ is


7
If a current is passed through a spring then the spring will
8
The mass of product liberated on anode in an electrochemical cell depends on (where $$t$$ is the time period for which the current is passed).
9
If $${\theta _1},$$ is the inversion temperature, $${\theta _n}$$ is the neutral temperature, $${\theta _c}$$ is the temperature of the cold junction, then
10
If an electron and a proton having same momentum enter perpendicular to a magnetic field, then
11
If in a circular coil $$A$$ of radius $$R,$$ current $$I$$ is flowing and in another coil $$B$$ of radius $$2R$$ a current $$2I$$ is flowing, then the ratio of the magnetic fields $${B_A}$$ and $${B_B}$$, produced by them will be
12
The time period of a charged particle undergoing a circular motion in a uniform magnetic field is independent of its
13
Wires $$1$$ and $$2$$ carrying currents $$i{}_1$$ and $$i{}_2$$ respectively are inclined at an angle $$\theta $$ to each other. What is the force on a small element $$dl$$ of wire $$2$$ at a distance of $$r$$ from wire $$1$$ (as shown in figure) due to the magnetic field of wire $$1$$?
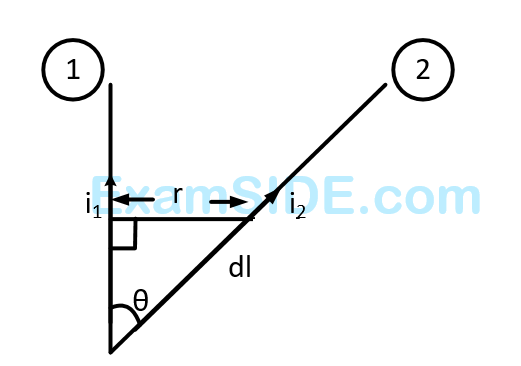

14
The power factor of $$AC$$ circuit having resistance $$(R)$$ and inductance $$(L)$$ connected in series and an angular velocity $$\omega $$ is
15
In a transformer, number of turns in the primary coil are $$140$$ and that in the secondary coil are $$280.$$ If current in primary coil is $$4A,$$ then that in the secondary coil is
16
An astronomical telescope has a large aperture to
17
Electromagnetic waves are transverse in nature is evident by
18
Wavelength of light used in an optical instrument are $${\lambda _1} = 4000\mathop A\limits^ \circ $$ and $${\lambda _2} = 5000\mathop A\limits^ \circ ,$$ then ratio of their respective resolving powers (corresponding to $${\lambda _1}$$ and $${\lambda _2}$$ ) is :
19
Which of the following is used in optical fibres?
20
A conducting square loop of side $$L$$ and resistance $$R$$ moves in its plane with a uniform velocity $$v$$ perpendicular to one of its sides. A magnetic induction $$B$$ constant in time and space, pointing perpendicular and into the plane at the loop exists everywhere with half the loop outside the field, as shown in figure. The induced $$emf$$ is


21
The inductance between $$A$$ and $$D$$ is


22
If $$13.6$$ $$eV$$ energy is required to ionize the hydrogen atom, then the energy required to remove an electron from $$n=2$$ is
23
At absolute zero, Si acts as
24
Sodium and copper have work functions $$2.3$$ $$eV$$ and $$4.5$$ $$eV$$ respectively. Then the ratio of the wavelengths is nearest to
25
Formation of covalent bonds in compounds exhibits
26
Capacitance (in $$F$$) of a spherical conductor with radius $$1$$ $$m$$ is
27
Moment of inertia of a circular wire of mass $$M$$ and radius $$R$$ about its diameter is
28
Energy required to move a body of mass $$m$$ from an orbit of radius $$2R$$ to $$3R$$ is
29
A spring of force constant $$800$$ $$N/m$$ has an extension of $$5$$ $$cm.$$ The work done in extending it from $$5$$ $$cm$$ to $$15$$ $$cm$$ is
30
One end of a mass-less rope, which passes over a mass-less and friction-less pulley $$P$$ is tied to a hook $$C$$ while the other end is free. Maximum tension that the rope can bear is $$360$$ $$N.$$ With what value of maximum safe acceleration (in $$m{s^{ - 2}}$$) can a man of $$60$$ $$kg$$ climb on the rope?
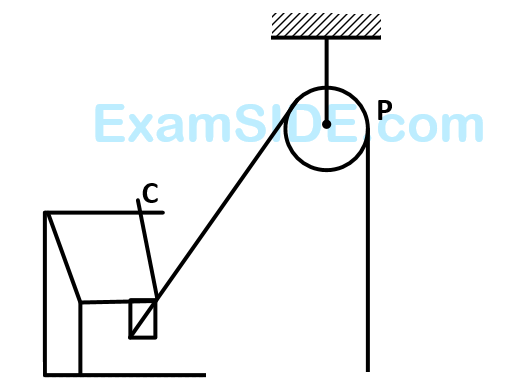

31
Infrared radiation is detected by
32
Heat given to a body which raises its temperature by $${1^ \circ }C$$ is
33
Which of the following is more close to a black body?
34
If mass-energy equivalence is taken into account, when water is cooled to form ice, the mass of water should
35
Cooking gas containers are kept in a lorry moving with uniform speed. The temperature of the gas molecules inside will
36
At what temperature is the $$r.m.s$$ velocity of a hydrogen molecule equal to that of an oxygen molecule at $${47^ \circ }C?$$
37
1 mole of a gas with $$\gamma = 7/5$$ is mixed with $$1$$ mole of a gas with $$\gamma = 5/3,$$ then the value of $$\gamma $$ for the resulting mixture is
38
Two spheres of the same material have radii $$1$$ $$m$$ and $$4$$ $$m$$ and temperatures $$4000$$ $$K$$ and $$2000$$ $$K$$ respectively. The ratio of the energy radiated per second by the first sphere to that by the second is
39
If a spring has time period $$T,$$ and is cut into $$n$$ equal parts, then the time period of each part will be
40
In a simple harmonic oscillator, at the mean position
41
A child swinging on a swing in sitting position, stands up, then the time period of the swing will
42
length of a string tied to two rigid supports is $$40$$ $$cm$$. Maximum length (wavelength in $$cm$$) of a stationary wave produced on it is
43
A tuning fork arrangement (pair) produces $$4$$ beats/sec with one fork of frequency $$288$$ $$cps.$$ A little wax is placed on the unknown fork and it then produces $$2$$ beats/sec. The frequency of the unknown fork is
44
Tube $$A$$ has bolt ends open while tube $$B$$ has one end closed, otherwise they are identical. The ratio of fundamental frequency of tube $$A$$ and $$B$$ is
45
A wave $$y=a$$ $$\sin \left( {\omega t - kx} \right)$$ on a string meets with another wave producing a node at $$x=0.$$ Then the equation of the unknown wave is
46
When temperature increases, the frequency of a tuning fork
47
On moving a charge of $$20$$ coulomb by $$2$$ $$cm,$$ $$2$$ $$J$$ of work is done, then the potential differences between the points is
48
If there are $$n$$ capacitors in parallel connected to $$V$$ volt source, then the energy stored is equal to
49
A charged particle $$q$$ is placed at the centre $$O$$ of cube of length $$L(ABCDEFGH).$$ Another same charge $$q$$ is placed at a distance $$L$$ from $$O$$. Then the electric flux through $$ABCD$$ is


50
If a charge $$q$$ is placed at the center of the line joining two equal charges $$Q$$ such that the system is in equilibrium then the value of $$q$$ is
51
If an ammeter is to be used in place of a voltmeter, then we must connect with the ammeter a
52
If suddenly the gravitational force of attraction between Earth and a satellite revolving around it becomes zero, then the satellite will
53
Identify the pair whose dimensions are equal
54
A ball whose kinetic energy E, is projected at an angle of $$45^\circ $$ to the horizontal. The kinetic energy of the ball at the highest point of its height will be
55
From a building two balls A and B are thrown such that A is thrown upwards and B downwards ( both vertically with the same speed ). If vA and vB are their respective velocities on reaching the ground, then
56
If a body looses half of its velocity on penetrating $$3$$ $$cm$$ in a wooden block, then how much will it penetrate more before coming to rest?
57
A lift is moving down with acceleration $$a.$$ A man in the lift drops a ball inside the lift. The acceleration of the ball as observed by the man in the lift and a man standing stationary on the ground are respectively
58
When forces $${F_1},\,\,{F_2},\,\,{F_3}$$ are acting on a particle of mass $$m$$ such that $${F_2}$$ and $${F_3}$$ are mutually perpendicular, then the particle remains stationary. If the force $${F_1}$$ is now removed then the acceleration of the particle is
59
Two forces are such that the sum of their magnitudes is $$18$$ $$N$$ and their resultant is $$12$$ $$N$$ which is perpendicular to the smaller force. Then the magnitudes of the forces are
60
A light string passing over a smooth light pulley connects two blocks of masses $${m_1}$$ and $${m_2}$$ (vertically). If the acceleration of the system is $$g/8$$, then the ratio of the masses is
61
Speeds of two identical cars are $$u $$ and $$4$$$$u $$ at the specific instant. The ratio of the respective distances in which the two cars are stopped from that instant is :
62
Three identical blocks of masses $$m=2$$ $$kg$$ are drawn by a force $$F=10.2$$ $$N$$ with an acceleration of $$0.6$$ $$m{s^{ - 2}}$$ on a frictionless surface, then what is the tension (in $$N$$) in the string between the blocks $$B$$ and $$C$$?
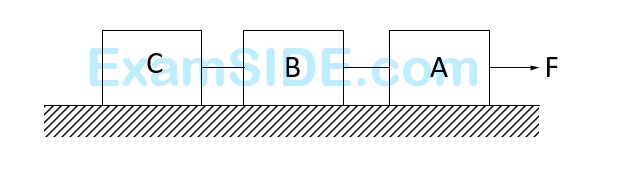

63
A cylinder of height $$20$$ $$m$$ is completely filled with water. The velocity of efflux of water (in $$m{s^{ - 1}}$$) through a small hole on the side wall of the cylinder near its bottom is
64
Initial angular velocity of a circular disc of mass $$M$$ is $${\omega _1}.$$ Then two small spheres of mass $$m$$ are attached gently to diametrically opposite points on the edge of the disc. What is the final angular velocity of the disc?
65
The minimum velocity (in $$m{s^{ - 1}}$$) with which a car driver must traverse a flat curve of radius 150 m and coefficient of friction $$0.6$$ to avoid skidding is
66
A solid sphere, a hollow sphere and a ring are released from top of an inclined plane (frictionless) so that they slide down the plane. Then maximum acceleration down the plane is for (no rolling)
67
A particle of mass $$m$$ moves along line PC with velocity $$v$$ as shown. What is the angular momentum of the particle about P?
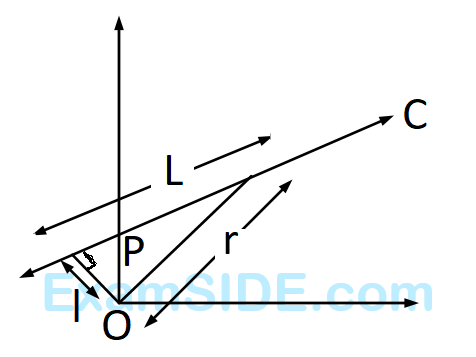

68
Two identical particles move towards each other with velocity $$2v$$ and $$v$$ respectively. The velocity of center of mass is
69
The kinetic energy needed to project a body of mass $$m$$ from the earth surface (radius $$R$$) to infinity is
70
The escape velocity of a body depends upon mass as