JEE Main 2019 (Online) 12th April Morning Slot
Paper was held on
Fri, Apr 12, 2019 3:30 AM
Chemistry
1
An example of a disproportionation reaction is :
2
The correct statement among the following is :
3
Given
CO3+ + e– $$ \to $$ CO2+ ; Eo = + 1.81 V
Pb4+ + 2e– $$ \to $$ Pb2+ ; Eo = + 1.67 V
Ce4+ + e– $$ \to $$ Ce3+ ; Eo = + 1.61 V
Bi3+ + 3e– $$ \to $$ Bi ; Eo = + 0.20 V
Oxidizing power of the species will increase in the order :
CO3+ + e– $$ \to $$ CO2+ ; Eo = + 1.81 V
Pb4+ + 2e– $$ \to $$ Pb2+ ; Eo = + 1.67 V
Ce4+ + e– $$ \to $$ Ce3+ ; Eo = + 1.61 V
Bi3+ + 3e– $$ \to $$ Bi ; Eo = + 0.20 V
Oxidizing power of the species will increase in the order :
4
Complete removal of both the axial ligands (along the z-axis) from an octahedral complex leads to which of
the following splitting patterns? (relative orbital energies not on scale).
5
5 moles of AB2 weigh 125 × 10–3
kg and 10 moles of A2B2 weigh 300 × 10–3
kg. The molar mass of A (MA)
and molar mass of B (MB) in kg mol are:
6
The increasing order of the pKb of the following compound is :
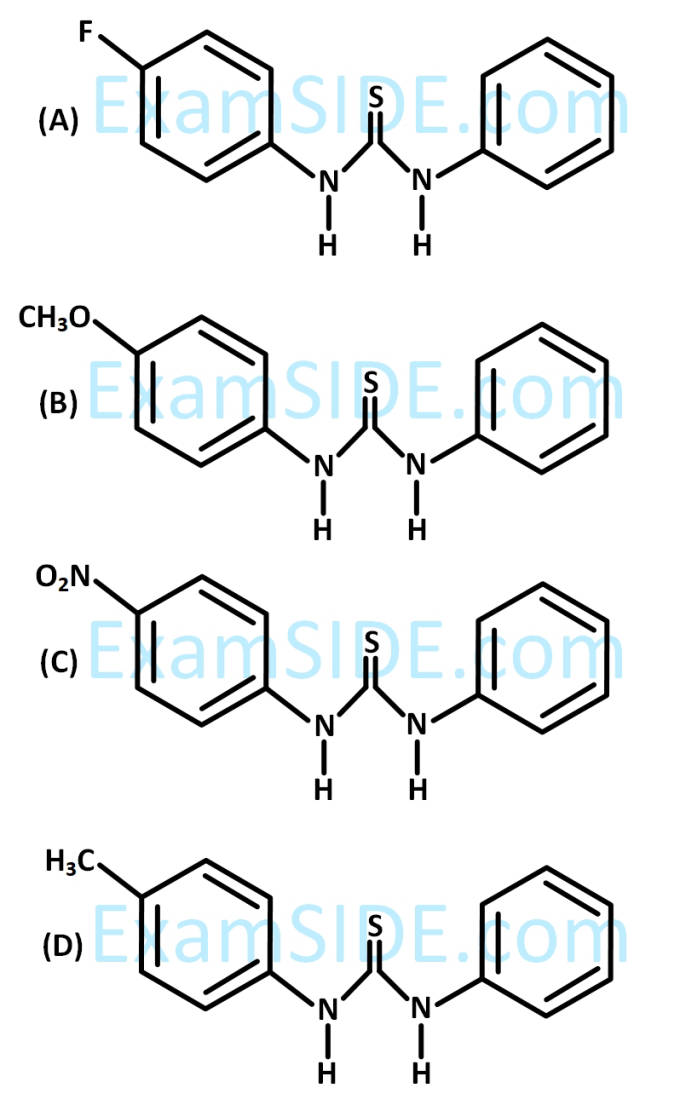

7
The group number, number of valence electrons, and valency of an element with atomic number 15,
respectively, are:
8
The complex ion that will lose its crystal field stabilization energy upon oxidation of its metal to +3 state is :

9
The major product(s) obtained in the following reaction is/are :
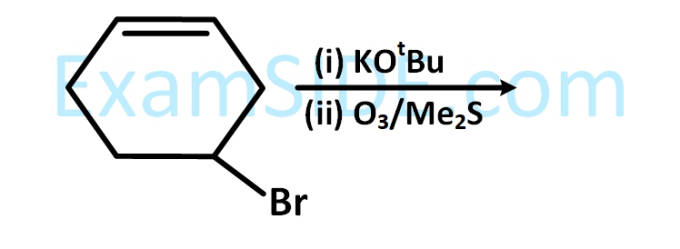

10
In the following reaction; xA $$ \to $$ yB
$${\log _{10}}\left[ { - {{d\left[ A \right]} \over {dt}}} \right] = {\log _{10}}\left[ {{{d\left[ B \right]} \over {dt}}} \right] + 0.3010$$
'A' and 'B' respectively can be :
$${\log _{10}}\left[ { - {{d\left[ A \right]} \over {dt}}} \right] = {\log _{10}}\left[ {{{d\left[ B \right]} \over {dt}}} \right] + 0.3010$$
'A' and 'B' respectively can be :
11
The major product of the following addition reaction is :
H3C–CH=CH2 $$\buildrel {C{l_2}/{H_2}O} \over \longrightarrow $$
H3C–CH=CH2 $$\buildrel {C{l_2}/{H_2}O} \over \longrightarrow $$
12
An ideal gas is allowed to expand form 1 L to 10 L against a constant external pressure of I bar. The work
done in kJ is :
13
But-2-ene on reaction with alkaline KMnO4 at elevated temperature followed by acidification will give :
14
The mole fraction of a solvent in aqueous solution of a solute is 0.8. The molality (in mol kg–1
) of the
aqueous solution is :
15
The electrons are more likely to be found :
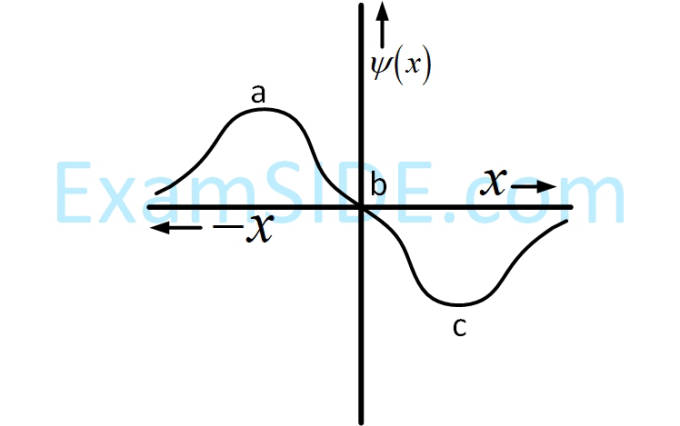

16
An organic compound 'A' is oxidizod with Na2O2 followed by boiling with HNO3. The resultant solution is
then treated with ammonium molybdate to yield a yellow precipitate.
Based on above observation, the element present in the given compound is:
Based on above observation, the element present in the given compound is:
17
Enthalpy of sublimation of iodine is 24 cal g–1
at 200 oC. If specific heat of I2(s) and l2 (vap) are 0.055 and
0.031 cal g–1K
–1
respectively, then enthalpy of sublimation of iodine at 250 oC in cal g–1
is :
18
Which of the following statements is not true about RNA?
19
The major products of the following reaction are :
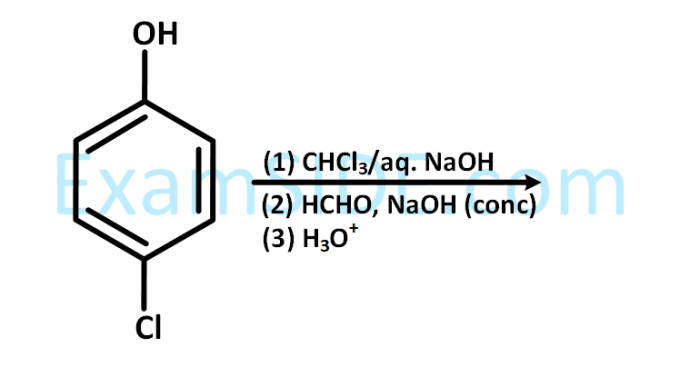

20
What is the molar solubility of Al(OH)3 in 0.2 M NaOH solution ? Given that, solubility product of Al(OH)3 = 2.4 × 10–24
:
21
Glucose and Galactose are having identical configuration in all the positions except position
22
The major product of the following reaction is :
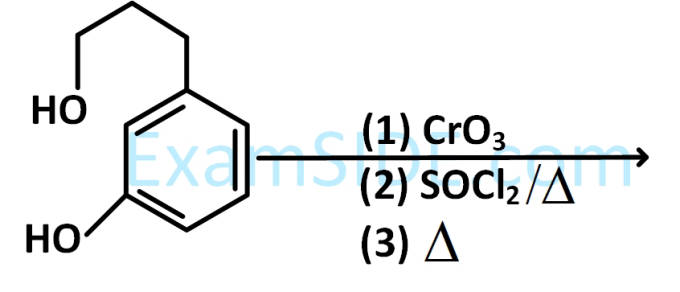

Mathematics
1
If ey
+ xy = e, the ordered pair $$\left( {{{dy} \over {dx}},{{{d^2}y} \over {d{x^2}}}} \right)$$ at x = 0 is equal to :
2
If $$\alpha $$ and $$\beta $$ are the roots of the equation 375x2
– 25x – 2 = 0, then $$\mathop {\lim }\limits_{n \to \infty } \sum\limits_{r = 1}^n {{\alpha ^r}} + \mathop {\lim }\limits_{n \to \infty } \sum\limits_{r = 1}^n {{\beta ^r}} $$ is equal to :
3
The equation |z – i| = |z – 1|, i = $$\sqrt { - 1} $$, represents :
4
If $$\int\limits_0^{{\pi \over 2}} {{{\cot x} \over {\cot x + \cos ecx}}} dx$$ = m($$\pi $$ + n), then m.n is equal to
5
For x $$ \in $$ (0, 3/2), let f(x) = $$\sqrt x $$ , g(x) = tan x and h(x) = $${{1 - {x^2}} \over {1 + {x^2}}}$$. If $$\phi $$ (x) = ((hof)og)(x), then $$\phi \left( {{\pi \over 3}} \right)$$
is equal to :
6
The integral $$\int {{{2{x^3} - 1} \over {{x^4} + x}}} dx$$ is equal to :
(Here C is a constant of integration)
(Here C is a constant of integration)
7
The number of ways of choosing 10 objects out of 31 objects of which 10 are identical and the remaining 21
are distinct, is :
8
If $$B = \left[ {\matrix{
5 & {2\alpha } & 1 \cr
0 & 2 & 1 \cr
\alpha & 3 & { - 1} \cr
} } \right]$$ is the inverse of a 3 × 3 matrix A, then the sum of all values of $$\alpha $$ for which
det(A) + 1 = 0, is :
9
If three of the six vertices of a regular hexagon are chosen at random, then the probability that the triangle
formed with these chosen vertices is equilateral is :
10
The value of $${\sin ^{ - 1}}\left( {{{12} \over {13}}} \right) - {\sin ^{ - 1}}\left( {{3 \over 5}} \right)$$ is equal to :
11
Let f : R $$ \to $$ R be a continuously differentiable function such that f(2) = 6 and f'(2) = $${1 \over {48}}$$. If $$\int\limits_6^{f\left( x \right)} {4{t^3}} dt$$ = (x - 2)g(x), then $$\mathop {\lim }\limits_{x \to 2} g\left( x \right)$$ is equal to :
12
Let Sn denote the sum of the first n terms of an A.P. If S4 = 16 and S6= – 48, then S10 is equal to :
13
The equation y = sinx sin (x + 2) – sin2
(x + 1) represents a straight line lying in :
14
A 2 m ladder leans against a vertical wall. If the top of the ladder begins to slide down the wall at the rate
25 cm/sec, then the rate (in cm/sec.) at which the bottom of the ladder slides away from the wall on the
horizontal ground when the top of the ladder is 1 m above the ground is :
15
Let $$\overrightarrow a = 3\widehat i + 2\widehat j + 2\widehat k$$ and $$\overrightarrow b = \widehat i + 2\widehat j - 2\widehat k$$ be two vectors. If a vector perpendicular to both the vectors
$$\overrightarrow a + \overrightarrow b $$ and $$\overrightarrow a - \overrightarrow b $$ has the magnitude 12 then one such vector is :
16
If the data x1, x2,......., x10 is such that the mean of first four of these is 11, the mean of the remaining six is
16 and the sum of squares of all of these is 2,000 ; then the standard deviation of this data is :
17
If A is a symmetric matrix and B is a skew-symmetric matrix such that A + B = $$\left[ {\matrix{
2 & 3 \cr
5 & { - 1} \cr
} } \right]$$, then AB is equal
to :
18
If the area (in sq. units) of the region {(x, y) : y2
$$ \le $$ 4x, x + y $$ \le $$ 1, x $$ \ge $$ 0, y $$ \ge $$ 0} is a $$\sqrt 2 $$ + b, then a – b is equal
to :
19
Consider the differential equation, $${y^2}dx + \left( {x - {1 \over y}} \right)dy = 0$$, If value of y is 1 when x = 1, then the value of x
for which y = 2, is :
20
The coefficient of x18 in the product
(1 + x) (1 – x)10 (1 + x + x2)9 is :
(1 + x) (1 – x)10 (1 + x + x2)9 is :
21
If the angle of intersection at a point where the two circles with radii 5 cm and 12 cm intersect is 90o, then
the length (in cm) of their common chord is :
22
If m is the minimum value of k for which the function f(x) = x$$\sqrt {kx - {x^2}} $$ is increasing in the interval [0,3]
and M is the maximum value of f in [0, 3] when k = m, then the ordered pair (m, M) is equal to :
Physics
1
A person of mass M is, sitting on a swing of length L and swinging with an angular amplitude $$\theta $$0. If the
person stands up when the swing passes through its lowest point, the work done by him, assuming that his
center of mass moves by a distance $$\ell $$($$\ell $$ << L), is close to;
2
Two moles of helium gas is mixed with three moles of hydrogen molecules (taken to be rigid). What is the
molar specific heat of mixture at constant volume ? (R = 8.3 J/mol K)
3
A concave mirror has radius of curvature of 40 cm. It is at the bottom of a glass that has water filled up to 5
cm (see figure). If a small particle is floating on the surface of water, its image as seen, from directly above
the glass, is at a distance d from the surface of water. The value of d is dose to: (Refractive index of water =
1.33)


4
To verify Ohm's law, a student connects the voltmeter across the battery as, shown in the figure. The
measured voltage is plotted as a function of the current, and the following graph is obtained :
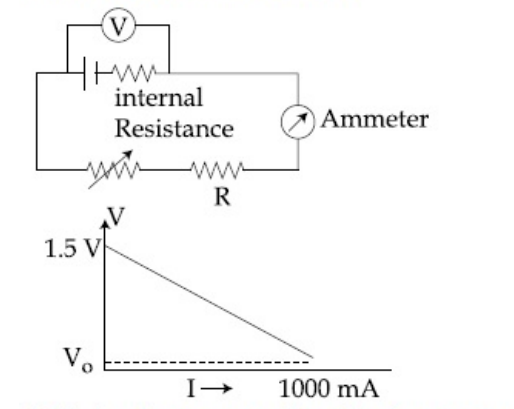
If V0 is almost zero, identify the correct statement :

If V0 is almost zero, identify the correct statement :
5
An electromagnetic wave is represented by the electric field $$\overrightarrow E = {E_0}\widehat n\sin \left[ {\omega t + \left( {6y - 8z} \right)} \right]$$
. Taking unit
vectors in x, y and z directions to be $$\widehat i,\widehat j,\widehat k$$
, the direction of propagation $$\widehat s$$, is :
6
At 40o C, a brass wire of 1 mm radius is hung from the ceiling. A small mass, M is hung from the free end of
the wire. When the wire is cooled down from 40oC to 20oC it regains its original length of 0.2 m. The value
of M is close to :
(Coefficient of linear expansion and Young’s modulus of brass are 10–5
/oC and 1011 N/m
2
, respectively; g=
10 ms–2
)
7
A sample of an ideal gas is taken through the cyclic process abca as shown in the figure. The change in the
internal energy of the gas along the path ca is –180 J. The gas absorbs 250 J of heat along the path ab and 60
J along the path bc. The work done by the gas along the path abc is:
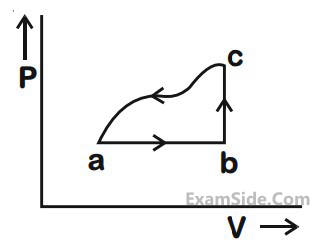

8
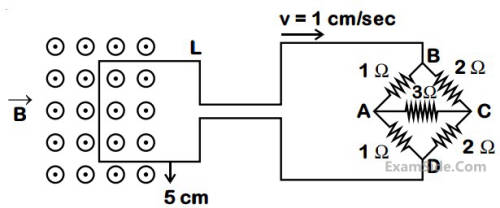
The figure shows a square loop L of side 5 cm which is connected to a network of resistances. The whole setup is moving towards right with a constant speed of 1 cm s-1. At some instant, a part of L is in a uniform
magnetic field of 1 T, perpendicular to the plane of the loop. If the resistance of L is 1.7 $$\Omega $$, the current in the
loop at that instant will be close to :

9
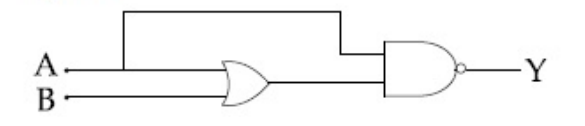
The truth table for the circuit given in the fig. is:

10
A galvanometer of resistance 100 $$\Omega $$ has 50 divisions on its scale and has sensitivitv of 20 $$\mu $$A/division. It is
to be converted to a voltmeter with three ranges of 0-2V, 0-10 V and 0-20 V. The appropriate circuit to do so
is
11
A point dipole $$\overrightarrow p = - {p_0}\widehat x$$
is kept at the origin. The potential and electric field due to this dipole on the
y-axis at a distance d are, respectively: (Take V= 0 at infinity)
12
Which of the following combinations has the dimension of electrical resistance ($$ \in $$0 is the permittivity of
vacuum and $$\mu $$0 is the permeability of vacuum)?
13
The trajectory of a projectile near the surface of the earth is given as y = 2x – 9x2
. If it were launched at an
angle $$\theta $$0 with speed v0 then (g = 10 ms–2) :
14
The resistive network shown below is connected to a D.C. source of 16 V. The power consumed by the
network is 4 Watt. The value of R is:


15
In a double slit experiment, when a thin film of thickness t having refractive index $$\mu $$. is introduced in front of
one of the slits, the maximum at the centre of the fringe pattern shifts by one fringe width. The value of t is
($$\lambda $$ is the wavelength of the light used) :
16
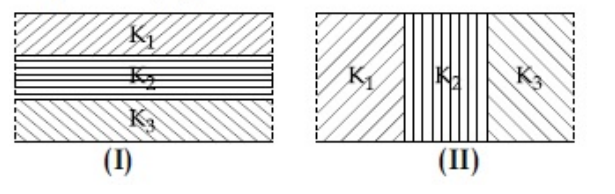
Two identical parallel plate capacitors, of capacitance C each, have plates of area A, separated by a distance
d. The space between the plates of the two capacitors, is filled with three dielectrics, of equal thickness and
dielectric constants K1, K2 and K3. The first capacitor is filled as shown in fig.I, and the second one is filled
as shown in fig II.
If these two modified capacitors are charged by the same potential V, the ratio of the energy stored in the
two, would be (E1 refers to capacitor (I) and E2 to capacitor (II)):

17
The value of numerical aperature of the objective lens of a microscope is 1.25. If light of wavelength 5000 $$\mathop A\limits^o $$
is used, the minimum separation between two points, to be seen as distinct, will be :
18
The stopping potential V0 (in volt) as a function of frequency ($$\upsilon $$) for a sodium emitter, is shown in the figure.
The work function of sodium, from the data plotted in the figure, will be:
(Given: Planck’s constant (h) = 6.63 × 10–34 Js, electron charges e = 1.6 × 10–19 C)
(Given: Planck’s constant (h) = 6.63 × 10–34 Js, electron charges e = 1.6 × 10–19 C)

19
A uniform rod of length $$\ell $$ is being rotated in a horizontal plane with a constant angular speed about an axis
passing through one of its ends. If the tension generated in the rod due to rotation is T(x) at a distance x from
the axis, then which of the following graphs depicts it most closely?
20
A thin ring of 10 cm radius carries a uniformly distributed charge. The ring rotates at a constant angular
speed of 40 $$\pi $$ rad s–1
about its axis, perpendicular to its plane. If the magnetic field at its centre is 3.8 × 10–9
T, then the charge carried by the ring is close to ($$\mu $$0 = 4$$\pi $$ × 10–7
N/A2
).
21
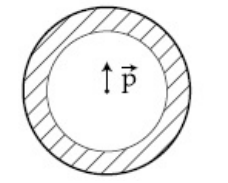
Shown in the figure is a shell made of a conductor. It has inner radius a and outer radius b, and carries charge
Q. At its centre is a dipole $$\overrightarrow P $$
as shown. In this case :

22
A shell is fired from a fixed artillery gun with an initial speed u such that it hits the target on the ground at a
distance R from it. If t1 and t2 are the values of the time taken by it to hit the target in two possible ways, the
product t1t2 is -
23
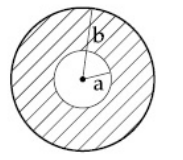
A circular disc of radius b has a hole of radius a at its centre (see figure). If the mass per unit area of the disc
varies as $$\left( {{{{\sigma _0}} \over r}} \right)$$
, then the radius of gyration of the disc about its axis passing through the centre is:

24
An excited He+
ion emits two photons in succession, with wavelengths 108.5 nm and 30.4 nm, in making a
transition to ground state. The quantum number n, corresponding to its initial excited state is (for photon of
wavelength $$\lambda $$, energy $$E = {{1240\,eV} \over {\lambda (in\,nm)}}$$) :
25
A progressive wave travelling along the positive x-direction is represented by y(x,t) = Asin(kx – $$\omega $$t + $$\phi $$). Its
snapshot at t = 0 is given in the figure.

For this wave, the phase $$\phi $$ is :

For this wave, the phase $$\phi $$ is :
26
A man (mass = 50 kg) and his son (mass = 20 kg) are standing on a frictionless surface facing each other. The
man pushes his son so that he starts moving at a speed of 0.70 ms–1 with respect to the man. The speed of the
man with respect to the surface is :
27
When M1 gram of ice at –10oC (specific heat = 0.5 cal g–1
oC–1
) is added to M2 gram of water at 50C, finally
no ice is left and the water is at 0°C. The value of latent heat of ice, in cal g–1
is :