JEE Main 2021 (Online) 1st September Evening Shift
Paper was held on
Wed, Sep 1, 2021 9:30 AM
Chemistry
1
Experimentally reducing a functional group cannot be done by which one of the following reagents?
2
Which one of the following given graphs represents the variation of rate constant (k) with temperature (T) for an endothermic reaction?
3
Identify A in the following reaction.


4
In the following sequence of reactions a compound A, (molecular formula C6H12O2) with a straight chain structure gives a C4 carboxylic acid. A is :


5
The Crystal Field Stabilization Energy (CFSE) and magnetic moment (spin-only) of an octahedral aqua complex of a metal ion (Mz+) are $$-$$0.8 $$\Delta$$0 and 3.87 BM, respectively. Identify (Mz+) :
6
Which one of the following compounds is aromatic in nature?
7
In the given chemical reaction, colors of the Fe2+ and Fe3+ ions, are respectively :
5Fe2+ + MnO$$_4^ - $$ + 8H+ $$\to$$ Mn2+ + 4H2O + 5Fe3+
5Fe2+ + MnO$$_4^ - $$ + 8H+ $$\to$$ Mn2+ + 4H2O + 5Fe3+
8
The stereoisomers that are formed by electrophilic addition of bromine to trans-but-2-ene is/are :
9
In the following sequence of reactions,

The compounds B and C respectively are :-

The compounds B and C respectively are :-
10
Given below are two statements :
Statement I : The nucleophilic addition of sodium hydrogen sulphite to an aldehyde or a ketone involves proton transfer to form a stable ion.
Statement II : The nucleophilic addition of hydrogen cyanide to an aldehyde or a ketone yields amine as final product.
In the light of the above statements, choose the most appropriate answer from the options given below :
Statement I : The nucleophilic addition of sodium hydrogen sulphite to an aldehyde or a ketone involves proton transfer to form a stable ion.
Statement II : The nucleophilic addition of hydrogen cyanide to an aldehyde or a ketone yields amine as final product.
In the light of the above statements, choose the most appropriate answer from the options given below :
11
Which one of the following gives the most stable Diazonium salt?
12
The potassium ferrocyanide solution gives a Prussian blue colour, when added to :
13
Number of paramagnetic oxides among the following given oxides is ____________.
Li2O, CaO, Na2O2, KO2, MgO and K2O
Li2O, CaO, Na2O2, KO2, MgO and K2O
14
Identify the element for which electronic configuration in +3 oxidation state is [Ar]3d5 :
15
The molar solubility of Zn(OH)2 in 0.1 M NaOH solution is x $$\times$$ 10$$-$$18 M. The value of x is _________ (Nearest integer)
(Given : The solubility product of Zn(OH)2 is 2 $$\times$$ 10$$-$$20)
(Given : The solubility product of Zn(OH)2 is 2 $$\times$$ 10$$-$$20)
16
For the reaction, 2NO2(g) $$\rightleftharpoons$$ N2O4(g), when $$\Delta$$S = $$-$$176.0 JK$$-$$1 and $$\Delta$$H = $$-$$57.8 kJ mol$$-$$1, the magnitude of $$\Delta$$G at 298 K for the reaction is ___________ kJ mol$$-$$1. (Nearest integer)
17
The sum of oxidation states of two silver ions in [Ag(NH3)2] [Ag(CN)2] complex is _____________.
18
The number of atoms in 8g of sodium is x $$\times$$ 1023. The value of x is ____________. (Nearest integer)
[Given : NA = 6.02 $$\times$$ 1023 mol$$-$$1
Atomic mass of Na = 23.0 u]
[Given : NA = 6.02 $$\times$$ 1023 mol$$-$$1
Atomic mass of Na = 23.0 u]
19
If 80 g of copper sulphate CuSO4 . 5H2O is dissolved in deionised water to make 5L of solution. The concentration of the copper sulphate solution is x $$\times$$ 10$$-$$3 mol L$$-$$1. The value of x is _____________.
[Atomic masses Cu : 63.54u, S : 32u, O : 16u, H : 1u]
[Atomic masses Cu : 63.54u, S : 32u, O : 16u, H : 1u]
20
A 50 watt bulb emits monochromatic red light of wavelength of 795 nm. The number of photons emitted per second by the bulb is x $$\times$$ 1020. The value of x is __________. [Given : h = 6.63 $$\times$$ 10$$-$$34 Js and c = 3.0 $$\times$$ 108 ms$$-$$1]
21
The spin-only magnetic moment value of $$B_2^ + $$ species is _____________ $$\times$$ 10$$-$$2 BM. (Nearest integer) [Given : $$\sqrt 3 $$ = 1.73]
22
If the conductivity of mercury at 0$$^\circ$$C is 1.07 $$\times$$ 106 S m$$-$$1 and the resistance of a cell containing mercury is 0.243$$\Omega$$, then the cell constant of the cell is x $$\times$$ 104 m$$-$$1. The value of x is ____________. (Nearest integer)
23
A peptide synthesized by the reactions of one molecule each of Glycine, Leucine, Aspartic acid and Histidine will have _________ peptide linkages.
Mathematics
1
Let f : R $$\to$$ R be a continuous function. Then $$\mathop {\lim }\limits_{x \to {\pi \over 4}} {{{\pi \over 4}\int\limits_2^{{{\sec }^2}x} {f(x)\,dx} } \over {{x^2} - {{{\pi ^2}} \over {16}}}}$$ is equal to :
2
$${\cos ^{ - 1}}(\cos ( - 5)) + {\sin ^{ - 1}}(\sin (6)) - {\tan ^{ - 1}}(\tan (12))$$ is equal to :
(The inverse trigonometric functions take the principal values)
(The inverse trigonometric functions take the principal values)
3
Consider the system of linear equations
$$-$$x + y + 2z = 0
3x $$-$$ ay + 5z = 1
2x $$-$$ 2y $$-$$ az = 7
Let S1 be the set of all a$$\in$$R for which the system is inconsistent and S2 be the set of all a$$\in$$R for which the system has infinitely many solutions. If n(S1) and n(S2) denote the number of elements in S1 and S2 respectively, then
$$-$$x + y + 2z = 0
3x $$-$$ ay + 5z = 1
2x $$-$$ 2y $$-$$ az = 7
Let S1 be the set of all a$$\in$$R for which the system is inconsistent and S2 be the set of all a$$\in$$R for which the system has infinitely many solutions. If n(S1) and n(S2) denote the number of elements in S1 and S2 respectively, then
4
Two squares are chosen at random on a chessboard (see figure). The probability that they have a side in common is :
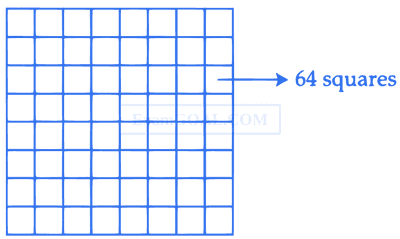

5
If y = y(x) is the solution curve of the differential equation $${x^2}dy + \left( {y - {1 \over x}} \right)dx = 0$$ ; x > 0 and y(1) = 1, then $$y\left( {{1 \over 2}} \right)$$ is equal to :
6
The function $$f(x) = {x^3} - 6{x^2} + ax + b$$ is such that $$f(2) = f(4) = 0$$. Consider two statements :
Statement 1 : there exists x1, x2 $$\in$$(2, 4), x1 < x2, such that f'(x1) = $$-$$1 and f'(x2) = 0.
Statement 2 : there exists x3, x4 $$\in$$ (2, 4), x3 < x4, such that f is decreasing in (2, x4), increasing in (x4, 4) and $$2f'({x_3}) = \sqrt 3 f({x_4})$$.
Then
Statement 1 : there exists x1, x2 $$\in$$(2, 4), x1 < x2, such that f'(x1) = $$-$$1 and f'(x2) = 0.
Statement 2 : there exists x3, x4 $$\in$$ (2, 4), x3 < x4, such that f is decreasing in (2, x4), increasing in (x4, 4) and $$2f'({x_3}) = \sqrt 3 f({x_4})$$.
Then
7
Let $${J_{n,m}} = \int\limits_0^{{1 \over 2}} {{{{x^n}} \over {{x^m} - 1}}dx} $$, $$\forall$$ n > m and n, m $$\in$$ N. Consider a matrix $$A = {[{a_{ij}}]_{3 \times 3}}$$ where $${a_{ij}} = \left\{ {\matrix{
{{j_{6 + i,3}} - {j_{i + 3,3}},} & {i \le j} \cr
{0,} & {i > j} \cr
} } \right.$$. Then $$\left| {adj{A^{ - 1}}} \right|$$ is :
8
The area, enclosed by the curves $$y = \sin x + \cos x$$ and $$y = \left| {\cos x - \sin x} \right|$$ and the lines $$x = 0,x = {\pi \over 2}$$, is :
9
The distance of line $$3y - 2z - 1 = 0 = 3x - z + 4$$ from the point (2, $$-$$1, 6) is :
10
The numbers of pairs (a, b) of real numbers, such that whenever $$\alpha$$ is a root of the equation x2 + ax + b = 0, $$\alpha$$2 $$-$$ 2 is also a root of this equation, is :
11
Let P1, P2, ......, P15 be 15 points on a circle. The number of distinct triangles formed by points Pi, Pj, Pk such that i +j + k $$\ne$$ 15, is :
12
The range of the function,
$$f(x) = {\log _{\sqrt 5 }}\left( {3 + \cos \left( {{{3\pi } \over 4} + x} \right) + \cos \left( {{\pi \over 4} + x} \right) + \cos \left( {{\pi \over 4} - x} \right) - \cos \left( {{{3\pi } \over 4} - x} \right)} \right)$$ is :
$$f(x) = {\log _{\sqrt 5 }}\left( {3 + \cos \left( {{{3\pi } \over 4} + x} \right) + \cos \left( {{\pi \over 4} + x} \right) + \cos \left( {{\pi \over 4} - x} \right) - \cos \left( {{{3\pi } \over 4} - x} \right)} \right)$$ is :
13
Let a1, a2, ..........., a21 be an AP such that $$\sum\limits_{n = 1}^{20} {{1 \over {{a_n}{a_{n + 1}}}} = {4 \over 9}} $$. If the sum of this AP is 189, then a6a16 is equal to :
14
The function f(x), that satisfies the condition
$$f(x) = x + \int\limits_0^{\pi /2} {\sin x.\cos y\,f(y)\,dy} $$, is :
$$f(x) = x + \int\limits_0^{\pi /2} {\sin x.\cos y\,f(y)\,dy} $$, is :
15
Let X be a random variable with distribution.
If the mean of X is 2.3 and variance of X is $$\sigma$$2, then 100 $$\sigma$$2 is equal to :
| x | $$ - $$2 | $$ - $$1 | 3 | 4 | 6 |
|---|---|---|---|---|---|
| P(X = x) | $${1 \over 5}$$ | a | $${1 \over 3}$$ | $${1 \over 5}$$ | b |
If the mean of X is 2.3 and variance of X is $$\sigma$$2, then 100 $$\sigma$$2 is equal to :
16
Let $$f(x) = {x^6} + 2{x^4} + {x^3} + 2x + 3$$, x $$\in$$ R. Then the natural number n for which $$\mathop {\lim }\limits_{x \to 1} {{{x^n}f(1) - f(x)} \over {x - 1}} = 44$$ is __________.
17
If for the complex numbers z satisfying | z $$-$$ 2 $$-$$ 2i | $$\le$$ 1, the maximum value of | 3iz + 6 | is attained at a + ib, then a + b is equal to ______________.
18
Let the points of intersections of the lines x $$-$$ y + 1 = 0, x $$-$$ 2y + 3 = 0 and 2x $$-$$ 5y + 11 = 0 are the mid points of the sides of a triangle $$\Delta $$ABC. Then, the area of the $$\Delta $$ABC is _____________.
19
Let f(x) be a polynomial of degree 3 such that
$$f(k) = - {2 \over k}$$ for k = 2, 3, 4, 5. Then the value of 52 $$-$$ 10f(10) is equal to :
$$f(k) = - {2 \over k}$$ for k = 2, 3, 4, 5. Then the value of 52 $$-$$ 10f(10) is equal to :
20
All the arrangements, with or without meaning, of the word FARMER are written excluding any word that has two R appearing together. The arrangements are listed serially in the alphabetic order as in the English dictionary. Then the serial number of the word FARMER in this list is ___________.
21
Let $$\overrightarrow a = 2\widehat i - \widehat j + 2\widehat k$$ and $$\overrightarrow b = \widehat i + 2\widehat j - \widehat k$$. Let a vector $$\overrightarrow v $$ be in the plane containing $$\overrightarrow a $$ and $$\overrightarrow b $$. If $$\overrightarrow v $$ is perpendicular to the vector $$3\widehat i + 2\widehat j - \widehat k$$ and its projection on $$\overrightarrow a $$ is 19 units, then $${\left| {2\overrightarrow v } \right|^2}$$ is equal to _____________.
22
Let [t] denote the greatest integer $$\le$$ t. The number of points where the function $$f(x) = [x]\left| {{x^2} - 1} \right| + \sin \left( {{\pi \over {[x] + 3}}} \right) - [x + 1],x \in ( - 2,2)$$ is not continuous is _____________.
23
A man starts walking from the point P($$-$$3, 4), touches the x-axis at R, and then turns to reach at the point Q(0, 2). The man is walking at a constant speed. If the man reaches the point Q in the minimum time, then $$50\left( {{{(PR)}^2} + {{(RQ)}^2}} \right)$$ is equal to ____________.
Physics
1
A cube is placed inside an electric field, $$\overrightarrow E = 150{y^2}\widehat j$$. The side of the cube is 0.5 m and is placed in the field as shown in the given figure. The charge inside the cube is :


2
A square loop of side 20 cm and resistance 1$$\Omega$$ is moved towards right with a constant speed v0. The right arm of the loop is in a uniform magnetic field of 5T. The field is perpendicular to the plane of the loop and is going into it. The loop is connected to a network of resistors each of value 4$$\Omega$$. What should be the value of v0 so that a steady current of 2 mA flows in the loop?


3
The temperature of an ideal gas in 3-dimensions is 300 K. The corresponding de-Broglie wavelength of the electron approximately at 300 K, is :
[me = mass of electron = 9 $$\times$$ 10$$-$$31 kg, h = Planck constant = 6.6 $$\times$$ 6.6 $$\times$$ 10$$-$$34 Js, kB = Boltzmann constant = 1.38 $$\times$$ 10$$-$$23 JK$$-$$1]
[me = mass of electron = 9 $$\times$$ 10$$-$$31 kg, h = Planck constant = 6.6 $$\times$$ 6.6 $$\times$$ 10$$-$$34 Js, kB = Boltzmann constant = 1.38 $$\times$$ 10$$-$$23 JK$$-$$1]
4
A body of mass 'm' dropped from a height 'h' reaches the ground with a speed of 0.8$$\sqrt {gh} $$. The value of workdone by the air-friction is :
5
The ranges and heights for two projectiles projected with the same initial velocity at angles 42$$^\circ$$ and 48$$^\circ$$ with the horizontal are R1, R2 and H1, H2 respectively. Choose the correct option :
6
A block of mass m slides on the wooden wedge, which in turn slides backward on the horizontal surface. The acceleration of the block with respect to the wedge is : Given m = 8 kg, M = 16 kg Assume all the surfaces shown in the figure to be frictionless.


7
Due to cold weather a 1 m water pipe of cross-sectional area 1 cm2 is filled with ice at $$-$$10$$^\circ$$C. Resistive heating is used to melt the ice. Current of 0.5A is passed through 4 k$$\Omega$$ resistance. Assuming that all the heat produced is used for melting, what is the minimum time required? (Given latent heat of fusion for water/ice = 3.33 $$\times$$ 105 J kg$$-$$1, specific heat of ice = 2 $$\times$$ 103 J kg$$-$$1 and density of ice = 103 kg/m3
8
A student determined Young's Modulus of elasticity using the formula $$Y = {{Mg{L^3}} \over {4b{d^3}\delta }}$$. The value of g is taken to be 9.8 m/s2, without any significant error, his observation are as following.
Then the fractional error in the measurement of Y is :
| Physical Quantity |
Least count of the Equipment used for measurement |
Observed value |
|---|---|---|
| Mass (M) | 1 g | 2 kg |
| Length of bar (L) | 1 mm | 1 m |
| Breadth of bar (b) | 0.1 mm | 4 cm |
| Thickness of bar (d) | 0.01 mm | 0.4 cm |
| Depression ($$\delta $$) | 0.01 mm | 5 mm |
Then the fractional error in the measurement of Y is :
9
Two resistors R1 = (4 $$\pm$$ 0.8) $$\Omega$$ and R2 = (4 $$\pm$$ 0.4) $$\Omega$$ are connected in parallel. The equivalent resistance of their parallel combination will be :
10
Following plots show magnetization (M) vs magnetizing field (H) and magnetic susceptibility ($$\chi $$) vs temperature (T) graph :

Which of the following combination will be represented by a diamagnetic material?

Which of the following combination will be represented by a diamagnetic material?
11
A glass tumbler having inner depth of 17.5 cm is kept on a table. A student starts pouring water ($$\mu$$ = 4/3) into it while looking at the surface of water from the above. When he feels that the tumbler is half filled, he stops pouring water. Up to what height, the tumbler is actually filled?
12
In the given figure, each diode has a forward bias resistance of 30$$\Omega$$ and infinite resistance in reverse bias. The current I1 will be :


13
For the given circuit the current i through the battery when the key in closed and the steady state has been reached is __________.
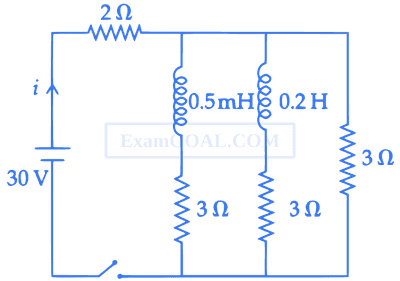

14
An object of mass 'm' is being moved with a constant velocity under the action of an applied force of 2N along a frictionless surface with following surface profile.

The correct applied force vs distance graph will be :

The correct applied force vs distance graph will be :
15
A mass of 5 kg is connected to a spring. The potential energy curve of the simple harmonic motion executed by the system is shown in the figure. A simple pendulum of length 4 m has the same period of oscillation as the spring system. What is the value of acceleration due to gravity on the planet where these experiments are performed?


16
A capacitor is connected to a 20 V battery through a resistance of 10$$\Omega$$. It is found that the potential difference across the capacitor rises to 2 V in 1 $$\mu$$s. The capacitance of the capacitor is __________ $$\mu$$F. Given : $$\ln \left( {{{10} \over 9}} \right) = 0.105$$
17
Four particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :


18
Electric field of plane electromagnetic wave propagating through a non-magnetic medium is given by
E = 20cos(2 $$\times$$ 1010 t $$-$$ 200x) V/m. The dielectric constant of the medium is equal to : (Take $$\mu$$r = 1)
E = 20cos(2 $$\times$$ 1010 t $$-$$ 200x) V/m. The dielectric constant of the medium is equal to : (Take $$\mu$$r = 1)
19
There are two infinitely long straight current carrying conductors and they are held at right angles to each other so that their common ends meet at the origin as shown in the figure given below. The ratio of current in both conductor is 1 : 1. The magnetic field at point P is ____________.
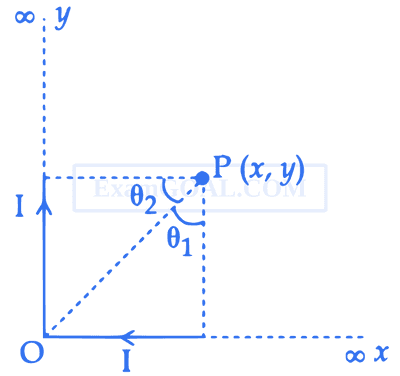

20
The temperature of 3.00 mol of an ideal diatomic gas is increased by 40.0$$^\circ$$C without changing the pressure of the gas. The molecules in the gas rotate but do not oscillate. If the ratio of change in internal energy of the gas to the amount of workdone by the gas is $${x \over {10}}$$. Then the value of x (round off to the nearest integer) is ___________. (Given R = 8.31 J mol$$-$$1 K$$-$$1)
21
The width of one of the two slits in a Young's double slit experiment is three times the other slit. If the amplitude of the light coming from a slit is proportional to the slit-width, the ratio of minimum to maximum intensity in the interference pattern is x : 4 where x is ____________.
22
Two satellites revolve around a planet in coplanar circular orbits in anticlockwise direction. Their period of revolutions are 1 hour and 8 hours respectively. The radius of the orbit of nearer satellite is 2 $$\times$$ 103 km. The angular speed of the farther satellite as observed from the nearer satellite at the instant when both the satellites are closest is $${\pi \over x}rad\,{h^{ - 1}}$$ where x is ____________.
23
When a body slides down from rest along a smooth inclined plane making an angle of 30$$^\circ$$ with the horizontal, it takes time T. When the same body slides down from the rest along a rough inclined plane making the same angle and through the same distance, it takes time $$\alpha$$T, where $$\alpha$$ is a constant greater than 1. The co-efficient of friction between the body and the rough plane is $${1 \over {\sqrt x }}\left( {{{{\alpha ^2} - 1} \over {{\alpha ^2}}}} \right)$$ where x = __________.
24
The average translational kinetic energy of N2 gas molecules at .............$$^\circ$$C becomes equal to the K.E. of an electron accelerated from rest through a potential difference of 0.1 volt. (Given kB = 1.38 $$\times$$ 10$$-$$23 J/K) (Fill the nearest integer).
25
A uniform heating wire of resistance 36$$\Omega$$ is connected across a potential difference of 240 V. The wire is then cut into half and potential difference of 240V is applied across each half separately. The ratio of power dissipation in first case to the total power dissipation in the second case would be 1 : x, where x is ____________
26
A steel rod with y = 2.0 $$\times$$ 1011 Nm$$-$$2 and $$\alpha$$ = 10$$-$$5 $$^\circ$$C$$-$$1 of length 4 m and area of cross-section 10 cm2 is heated from 0$$^\circ$$C to 400$$^\circ$$C without being allowed to extend. The tension produced in the rod is x $$\times$$ 105 N where the value of x is ____________.
27
A 2 kg steel rod of length 0.6 m is clamped on a table vertically at its lower end and is free to rotate in vertical plane. The upper end is pushed so that the rod falls under gravity, ignoring the friction due to clamping at its lower end, the speed of the free end of rod when it passes through its lowest position is ____________ ms$$-$$1. (Take g = 10 ms$$-$$2)
28
An engine is attached to a wagon through a shock absorber of length 1.5 m. The system with a total mass of 40,000 kg is moving with a speed of 72 kmh$$-$$1 when the brakes are applied to bring it to rest. In the process of the system being brought to rest, the spring of the shock absorber gets compressed by 1.0 m. If 90% of energy of the wagon is lost due to friction, the spring constant is ____________ $$\times$$ 105 N/m.