JEE Main 2019 (Online) 10th April Evening Slot
Paper was held on
Wed, Apr 10, 2019 9:30 AM
Chemistry
1
The increasing order of nucleophilicity of the following nucleophiles is :
(a) CH3CO2$$-$$ (b) H2O
(c) CH3SO3$$-$$ (d) $$\mathop O\limits^ - H$$
(a) CH3CO2$$-$$ (b) H2O
(c) CH3SO3$$-$$ (d) $$\mathop O\limits^ - H$$
2
The major product 'Y' in the following reaction is :


3
Which one of the following graphs between molar conductivity ($${\Lambda _m}$$) versus $$\sqrt C $$ is correct ?
4
The crystal field stabilization energy (CFSE) of [Fe(H2O)6]Cl2 and K2[NiCl4] respectively, are :
5
Which of these factors does not govern the stability of a conformation in acyclic compounds?
6
The pH of a 0.02 M NH4Cl solution will be :
[given Kb (NH4OH) = 10–5 and log 2 = 0.301]
[given Kb (NH4OH) = 10–5 and log 2 = 0.301]
7
For the reaction,
2SO2(g) + O2(g) = 2SO3(g), $$\Delta $$H = –57.2 kJ mol–1 and KC = 1.7 × 1016
Which of the following statement is incorrect ?
2SO2(g) + O2(g) = 2SO3(g), $$\Delta $$H = –57.2 kJ mol–1 and KC = 1.7 × 1016
Which of the following statement is incorrect ?
8
The minimum amount of O2(g) consumed per gram of reactant is for the reaction :
(Given atomic mass : Fe = 56, O = 16, Mg = 24, P = 31, C = 12, H = 1)
(Given atomic mass : Fe = 56, O = 16, Mg = 24, P = 31, C = 12, H = 1)
9
The difference between $$\Delta $$H and $$\Delta $$U ($$\Delta $$H – $$\Delta $$U), when the combustion of one mole of heptane(l) is carried
out at a temperature T, is equal to :
10
1 g of a non-volatile non-electrolyte solute is dissolved in 100 g of two different solvents A and B whose
ebullioscopic constants are in the ratio of 1 : 5. The ratio of the elevation in their boiling points, $${{\Delta {T_b}(A)} \over {\Delta {T_b}(B)}}$$, is :
11
The ratio of the shortest wavelength of two spectral series of hydrogen spectrum is found to be about 9. The
spectral series are :
12
The correct order of the first ionization enthalpies is :
13
Compound A(C9H10O) shows positive iodoform test. Oxidation of A with KMnO4/KOH given acid
B(C8H6O4). Anhydride of B is used for the preparation of phenolphthalein. Compound A is:
14
The major product 'Y' in the following reactions is :


15
For the reaction of H2 with I2, the rate constant is 2.5 × 10–4 dm3
mol–1s–1
at 327°C and 1.0 dm3
mol–1
at
527°C. The activation energy for the reaction, in kJ mole–1
is : (R = 8.314 JK–1
mol–1
)
16
In chromatography, which of the following statements is incorrect for Rf ?
17
The INCORRECT statement is :
18
The highest possible oxidation states of uranium and plutonium, respectively are :
19
Number of stereo centers present in linear and cyclic structures of glucose are respectively :
20
The noble gas that does not occur in the atmosphere is :
21
Which of the following is not a correct method of the preparation of benzylamine from cyanobenzene ?
22
The major product obtained in the given reaction is :


Mathematics
1
Let f(x) = loge(sin x), (0 < x < $$\pi $$) and g(x) = sin–1
(e–x
), (x $$ \ge $$ 0). If $$\alpha $$ is a positive real number such that
a = (fog)'($$\alpha $$) and b = (fog)($$\alpha $$), then :
2
A spherical iron ball of radius 10 cm is coated with a layer of ice of uniform thickness that melts at a rate of
50 cm3
/min. When the thickness of the ice is 5 cm, then the rate at which the thickness (in cm/min) of the ice
decreases, is :
3
The number of real roots of the equation
5 + |2x – 1| = 2x (2x – 2) is
5 + |2x – 1| = 2x (2x – 2) is
4
If $$\mathop {\lim }\limits_{x \to 1} {{{x^2} - ax + b} \over {x - 1}} = 5$$, then a + b is equal to :
5
Minimum number of times a fair coin must be tossed so that the probability of getting at least one head is
more than 99% is :
6
Let $$a$$, b and c be in G.P. with common ratio r, where $$a$$ $$ \ne $$ 0 and 0 < r $$ \le $$ $${1 \over 2}$$
. If 3$$a$$, 7b and 15c are the first three
terms of an A.P., then the 4th term of this A.P. is :
7
The distance of the point having position vector $$ - \widehat i + 2\widehat j + 6\widehat k$$
from the straight line passing through the point
(2, 3, – 4) and parallel to the vector, $$6\widehat i + 3\widehat j - 4\widehat k$$ is :
8
If $${\cos ^{ - 1}}x - {\cos ^{ - 1}}{y \over 2} = \alpha $$,where –1 $$ \le $$ x $$ \le $$ 1, – 2 $$ \le $$ y $$ \le $$ 2, x $$ \le $$ $${y \over 2}$$
, then for all x, y, 4x2
– 4xy cos $$\alpha $$ + y2
is equal
to :
9
Let a1, a2, a3,......be an A.P. with a6 = 2. Then the common difference of this A.P., which maximises the
product a1a4a5, is :
10
If both the mean and the standard deviation of 50 observations x1, x2,..., x50 are equal to 16, then the mean of (x1 – 4)2
, (x2 – 4)2
,....., (x50 – 4)2
is :
11
Lines are drawn parallel to the line 4x – 3y + 2 = 0, at a distance
$${3 \over 5}$$
from the origin. Then which one of the
following points lies on any of these lines ?
12
Let y = y(x) be the solution of the differential equation,
$${{dy} \over {dx}} + y\tan x = 2x + {x^2}\tan x$$, $$x \in \left( { - {\pi \over 2},{\pi \over 2}} \right)$$, such that y(0) = 1. Then :
$${{dy} \over {dx}} + y\tan x = 2x + {x^2}\tan x$$, $$x \in \left( { - {\pi \over 2},{\pi \over 2}} \right)$$, such that y(0) = 1. Then :
13
If $$\int {{x^5}} {e^{ - {x^2}}}dx = g\left( x \right){e^{ - {x^2}}} + c$$, where c is a constant of integration, then $$g$$(–1) is equal to :
14
Suppose that 20 pillars of the same height have been erected along the boundary of a circular stadium. If the
top of each pillar has been connected by beams with the top of all its non-adjacent pillars, then the total
number of beams is :
15
The integral $$\int\limits_{\pi /6}^{\pi /3} {{{\sec }^{2/3}}} x\cos e{c^{4/3}}xdx$$ is equal to :
16
The area (in sq.units) of the region bounded by the curves y = 2x
and y = |x + 1|, in the first quadrant is :
17
If z and w are two complex numbers such that |zw| = 1 and arg(z) – arg(w) = $${\pi \over 2}$$
, then :
18
The sum of the real roots of the equation
$$\left| {\matrix{ x & { - 6} & { - 1} \cr 2 & { - 3x} & {x - 3} \cr { - 3} & {2x} & {x + 2} \cr } } \right| = 0$$, is equal to :
$$\left| {\matrix{ x & { - 6} & { - 1} \cr 2 & { - 3x} & {x - 3} \cr { - 3} & {2x} & {x + 2} \cr } } \right| = 0$$, is equal to :
19
If 5x + 9 = 0 is the directrix of the hyperbola 16x2
– 9y2
= 144, then its corresponding focus is :
20
The smallest natural number n, such that the coefficient of x in the expansion of $${\left( {{x^2} + {1 \over {{x^3}}}} \right)^n}$$ is nC23, is :
21
Let $$\lambda $$ be a real number for which the system of linear equations x + y + z = 6, 4x + $$\lambda $$y – $$\lambda $$z = $$\lambda $$ – 2,
3x + 2y – 4z = – 5 has infinitely many solutions. Then $$\lambda $$ is a root of the quadratic equation:
Physics
1
A square loop is carrying a steady current I and the magnitude of its magnetic dipole moment is m. if this
square loop is changed to a circular loop and it carries the same current, the magnitude of the magnetic dipole
moment of circular loop will be:
2
A plane is inclined at an angle $$\alpha $$ = 30° with respect to the horizontal. A particle is projected with a speed u =
2 ms–1
, from the base of the plane, making an angle $$\theta $$ = 15° with respect to the plane as shown in the figure.
the distance from the base, at which the particle hits the plane is close to :
(Take g = 10 ms –2)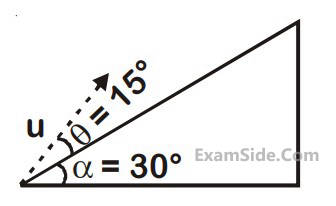
(Take g = 10 ms –2)

3
The time dependence of the position of a particle of mass m = 2 is given by $$\overrightarrow r \left( t \right) = 2t\widehat i - 3{t^2}\widehat j$$
. Its angular
momentum, with respect to the origin, at time t = 2 is
4
The magnitude of the magnetic field at the centre of an equilateral triangular loop of side 1 m which is
carrying a current of 10 A is :
[Take $$\mu $$0 = 4$$\pi $$ × 10–7 NA–2]
[Take $$\mu $$0 = 4$$\pi $$ × 10–7 NA–2]
5
Two blocks A and B of masses mA = 1 kg and mB = 3 kg are kept on the table as shown in figure. The coefficient of friction between A and B is 0.2 and between B and the surface of the table is also 0.2. The maximum force F that can be applied on B horizontally, so that the block A does not slide over the block B is :
[Take g = 10 m/s2]
[Take g = 10 m/s2]

6
Light is incident normally on a completely absorbing surface with an energy flux of 25 W cm–2. If the surface
has an area of 25 cm2, the momentum transferred to the surface in 40 min time duration will be :
7
In Li+ +, electron in first Bohr orbit is excited to a level by a radiation of wavelength $$\lambda $$. When the ion gets
deexcited to the ground state in all possible ways (including intermediate emissions), a total of six spectral
lines are observed. What is the value of $$\lambda $$?
(Given : H = 6.63 × 10–34 Js; c = 3 × 108 ms –1)
(Given : H = 6.63 × 10–34 Js; c = 3 × 108 ms –1)
8
A solid sphere of mass M and radius R is divided into two unequal parts. The first part has a mass of $${{7M} \over 8}$$
and is converted into a uniform disc of radius 2R. The second part is converted into a uniform solid sphere.
Let I1 be the moment of inertia of the disc about its axis and I2 be the moment of inertia of the new sphere
about its axis. The ratio I1/I2 is given by :
9
A spaceship orbits around a planet at a height of 20 km from its surface. Assuming that only gravitational
field of the planet acts on the spaceship, what will be the number of complete revolutions made by the
spaceship in 24 hours around the planet?
[Given ; Mass of planet = 8 × 1022 kg, Radius of planet = 2 × 106 m, Gravitational constant G = 6.67 × 10–11 Nm2 /kg2]
[Given ; Mass of planet = 8 × 1022 kg, Radius of planet = 2 × 106 m, Gravitational constant G = 6.67 × 10–11 Nm2 /kg2]
10
In a Young's double slit experiment, the ratio of the slit's width is 4 : 1. The ratio of the intensity of maxima to minima, close to the central fringe on the screen, will be :
11
The correct figure that shows, schematically, the wave pattern produced by superposition of two waves of
frequencies 9 Hz and 11 Hz, is :
12
In an experiment, brass and steel wires of length 1 m each with areas of cross section 1mm2
are used. The
wires are connected in series and one end of the combined wire is connected to a rigid support and other end
is subjected to elongation. The stress required to produce a net elongation of 0.2 mm is,
[Given, the Young's Modulus for steel and brass are, respectively, 120 × 109
N/m2
and 60 × 109
N/m2]
13
A submarine experiences a pressure of 5.05 × 106
Pa at a depth of d1 in a sea. When it goes further to a depth
of d2, it experiences a pressure of 8.08 × 106
Pa. Then d2 –d1 is approximately (density of water = 103
kg/m3
and acceleration due to gravity = 10 ms–2
) :
14
Water from a tap emerges vertically downwards with an initial speed of 1.0 ms–1
. The cross-sectional area of
the tap is 10–4 m2. Assume that the pressure is constant throughout the stream of water and that the flow is streamlined. The cross-sectional area of the stream, 0.15 m below the tap would be : (Take g = 10 ms–2)
15
One mole of ideal gas passes through a process where pressure and volume obey the relation
$$P = {P_0}\left[ {1 - {1 \over 2}{{\left( {{{{V_0}} \over V}} \right)}^2}} \right]$$.
Here P0 and V0 are constants. Calculate the change in the temperature of the gas if its
volume changes form V0 to 2V0
16
Space between two concentric conducting spheres of radii a and b (b > a) is filled with a medium of
resistivity $$\rho $$. The resistance between the two spheres will be :
17
A metal coin of mass 5 g and radius 1 cm is fixed to a thin stick AB of negligible mass as shown in the
figure. The system is initially at rest. The constant torque, that will make the system rotate about AB at 25
rotations per second in 5s, is close to :
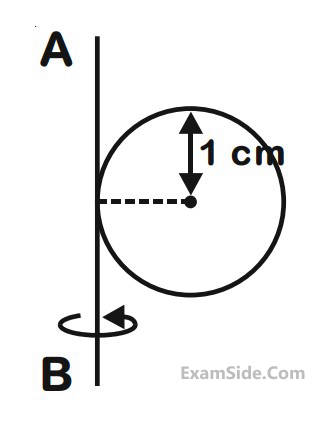

18
A coil of self inductance 10 mH and resistance 0.1 $$\Omega $$ is connected through a switch to a battery of internal
resistance 0.9 $$\Omega $$. After the switch is closed, the time taken for the current to attain 80% of the saturation
value is: [take ln 5 = 1.6]
19
The figure represents a voltage regulator circuit using a Zener diode. The breakdown voltage of the Zener
diode is 6 V and the load resistance is, RL = 4k$$\Omega $$. The series resistance of the circuit is Ri
= 1 k$$\Omega $$. If the
battery voltage VB varies from 8 V to 16 V, what are the minimum and maximum values of the current
through Zener diode?


20
A bullet of mass 20 g has an initial speed of 1 ms–1
, just before it starts penetrating a mud wall of thickness
20 cm. If the wall offers a mean resistance of 2.5 × 10–2 N, the speed of the bullet after emerging from the
other side of the wall is close to :
21
In the formula X = 5YZ2
, X and Z have dimensions of capacitance and magnetic field, respectively. What are
the dimensions of Y in SI units?
22
In free space, a particle A of charge 1$$\mu $$C is held fixed at a point P. Another particle B of the same charge and
mass 4$$\mu $$g is kept at a distance of 1 mm from P. If B is released, then its velocity at a distance of 9 mm from P
is :
$$\left[ {Take\,{1 \over {4\pi { \in _0}}} = 9 \times {{10}^9}N{m^2}{C^{ - 2}}} \right]$$
23
When heat Q is supplied to a diatomic gas of rigid molecules, at constant volume its temperature increases by
$$\Delta $$T. the heat required to produce the same change in temperature, at a constant pressure is :
24
The elastic limit of brass is 379 MPa. What should be the minimum diameter of a brass rod if it is to support
a 400 N load without exceeding its elastic limit?
25
A 2 mW laser operates at wavelength of 500 nm. The number of photons that will be emitted per second is :
[Given Planck's constant h = 6.6 × 10–34 Js, speed of light c = 3.0 × 108
m/s]
26
A cubical block of side 0.5 m floats on water with 30% of its volume under water. What is the maximum
weight that can be put on the block without fully submerging it under water? [Take, density of water = 103
kg/m3]
27
The graph shows how the magnification m produced by a thin lens varies with image distance v. What is the focal length of the lens used?


28
A simple pendulum of length L is placed between the plates of a parallel plate capacitor having electric field
E, as shown in figure. Its bob has mass m and charge q. The time period of the pendulum is given by :

