JEE Main 2020 (Online) 2nd September Morning Slot
Paper was held on
Wed, Sep 2, 2020 3:30 AM
Chemistry
1
The Gibbs change (in J) for the given reaction at
[Cu2+] = [Sn2+] = 1 M and 298K is :
Cu(s) + Sn2+(aq.) $$ \to $$ Cu2+(aq.) + Sn(s);
($$E_{S{n^{2 + }}|Sn}^0 = - 0.16\,V$$,
$$E_{C{u^{2 + }}|Cu}^0 = 0.34\,V$$)
Take F = 96500 C mol–1)
[Cu2+] = [Sn2+] = 1 M and 298K is :
Cu(s) + Sn2+(aq.) $$ \to $$ Cu2+(aq.) + Sn(s);
($$E_{S{n^{2 + }}|Sn}^0 = - 0.16\,V$$,
$$E_{C{u^{2 + }}|Cu}^0 = 0.34\,V$$)
Take F = 96500 C mol–1)
2
The oxidation states of iron atoms in
compounds (A), (B) and (C), respectively, are x,
y and z. The sum of x, y and z is ________.
Na4[Fe(CN)5(NOS)]
(A)
Na4[FeO4]
(B)
[Fe2(CO)9]
(C)
Na4[Fe(CN)5(NOS)]
(A)
Na4[FeO4]
(B)
[Fe2(CO)9]
(C)
3
The internal energy change (in J) When 90 g of
water undergoes complete evaporation at
100oC is ____________.
(Given : $$\Delta $$Hvap for water at 373 K = 41 kJ/mol,
R = 8.314 JK–1 mol–1)
(Given : $$\Delta $$Hvap for water at 373 K = 41 kJ/mol,
R = 8.314 JK–1 mol–1)
4
The number of chiral carbons present in the
molecule given below is _____ .


5
The increasing order of the following
compounds towards HCN addition is :
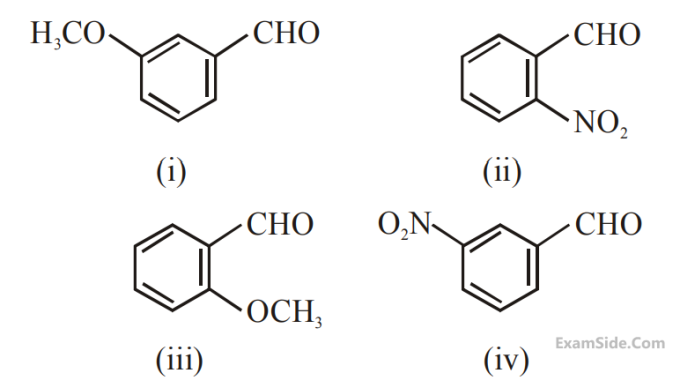

6
The major aromatic product C in the following
reaction sequence will be :
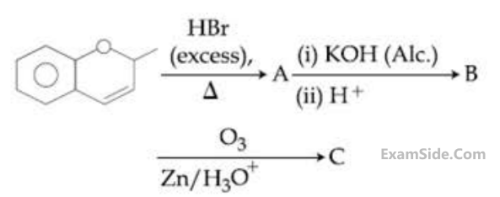

7
In general the property (magnitudes only) that
show an opposite trend in comparison to other
properties across a period is
8
While titrating dilute HCl solution with aqueous
NaOH, which of the following will not be
required?
9
The IUPAC name for the following compound
is
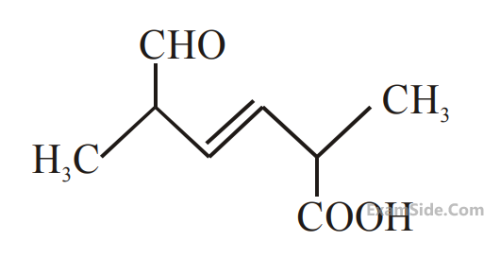

10
The major product in the following reaction is :
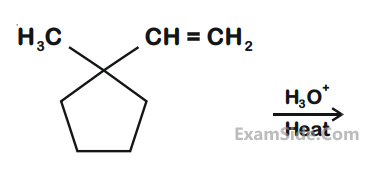

11
Which of the following compunds will show
retention in configuration on nucleophilic
substitution by OH– ion?
12
Consider that a d6 metal ion (M2+) forms a
complex with aqua ligands, and the spin only
magnetic moment of the complex is 4.90 BM.
The geometry and the crystal field stabilization
energy of the complex is
13
For octahedral Mn(II) and tetrahedral Ni(II)
complexes, consider the following statements:
(I) both the complexes can be high spin.
(II) Ni(II) complex can very rarely be low spin.
(III) with strong field ligands, Mn(II) complexes can be low spin.
(IV)aqueous solution of Mn(II) ions is yellow in colour.
The correct statements are :
(I) both the complexes can be high spin.
(II) Ni(II) complex can very rarely be low spin.
(III) with strong field ligands, Mn(II) complexes can be low spin.
(IV)aqueous solution of Mn(II) ions is yellow in colour.
The correct statements are :
14
Consider the following rections:
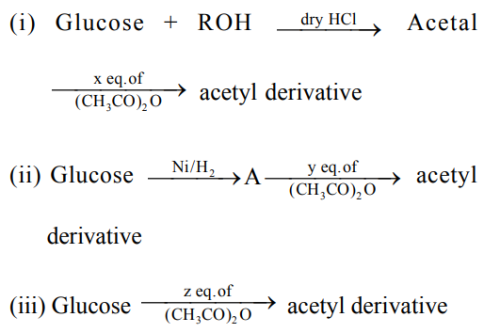
'x', 'y' and 'z' in these reactions are respectively.

'x', 'y' and 'z' in these reactions are respectively.
15
An open beaker of water in equilibrium with
water vapour is in a sealed container. When a
few grams of glucose are added to the beaker
of water, the rate at which water molecules :
16
For the following Assertion and Reason, the
correct option is
Assertion (A): When Cu (II) and sulphide ions are mixed, they react together extremely quickly to give a solid.
Reason (R): The equilibrium constant of
Cu2+(aq) + S2–(aq) ⇌ CuS(s) is high because the solubility product is low.
Assertion (A): When Cu (II) and sulphide ions are mixed, they react together extremely quickly to give a solid.
Reason (R): The equilibrium constant of
Cu2+(aq) + S2–(aq) ⇌ CuS(s) is high because the solubility product is low.
17
The figure that is not a direct manifestation of
the quantum nature of atoms is :
18
If AB4 molecule is a polar molecule, a possible
geometry of AB4 is
19
In Carius method of estimation of halogen,
0.172 g of an organic compound showed
presence of 0.08 g of bromine. Which of these
is the correct structure of the compound?
Mathematics
1
Let S be the set of all $$\lambda $$ $$ \in $$ R for which the system
of linear equations
2x – y + 2z = 2
x – 2y + $$\lambda $$z = –4
x + $$\lambda $$y + z = 4
has no solution. Then the set S :
2x – y + 2z = 2
x – 2y + $$\lambda $$z = –4
x + $$\lambda $$y + z = 4
has no solution. Then the set S :
2
If a function f(x) defined by
$$f\left( x \right) = \left\{ {\matrix{ {a{e^x} + b{e^{ - x}},} & { - 1 \le x < 1} \cr {c{x^2},} & {1 \le x \le 3} \cr {a{x^2} + 2cx,} & {3 < x \le 4} \cr } } \right.$$
be continuous for some $$a$$, b, c $$ \in $$ R and f'(0) + f'(2) = e, then the value of of $$a$$ is :
$$f\left( x \right) = \left\{ {\matrix{ {a{e^x} + b{e^{ - x}},} & { - 1 \le x < 1} \cr {c{x^2},} & {1 \le x \le 3} \cr {a{x^2} + 2cx,} & {3 < x \le 4} \cr } } \right.$$
be continuous for some $$a$$, b, c $$ \in $$ R and f'(0) + f'(2) = e, then the value of of $$a$$ is :
3
Area (in sq. units) of the region outside
$${{\left| x \right|} \over 2} + {{\left| y \right|} \over 3} = 1$$ and inside the ellipse $${{{x^2}} \over 4} + {{{y^2}} \over 9} = 1$$ is :
$${{\left| x \right|} \over 2} + {{\left| y \right|} \over 3} = 1$$ and inside the ellipse $${{{x^2}} \over 4} + {{{y^2}} \over 9} = 1$$ is :
4
Box I contains 30 cards numbered 1 to 30 and
Box II contains 20 cards numbered 31 to 50. A
box is selected at random and a card is drawn
from it. The number on the card is found to be
a non-prime number. The probability that the
card was drawn from Box I is :
5
Let
$$\alpha $$ > 0,
$$\beta $$ > 0 be such that
$$\alpha $$3 + $$\beta $$2 = 4. If the maximum value of the term independent of x in
the binomial expansion of $${\left( {\alpha {x^{{1 \over 9}}} + \beta {x^{ - {1 \over 6}}}} \right)^{10}}$$ is 10k,
then k is equal to :
$$\alpha $$3 + $$\beta $$2 = 4. If the maximum value of the term independent of x in
the binomial expansion of $${\left( {\alpha {x^{{1 \over 9}}} + \beta {x^{ - {1 \over 6}}}} \right)^{10}}$$ is 10k,
then k is equal to :
6
Let A be a 2 $$ \times $$ 2 real matrix with entries from
{0, 1} and |A|
$$ \ne $$ 0. Consider the following two
statements :
(P) If A $$ \ne $$ I2 , then |A| = –1
(Q) If |A| = 1, then tr(A) = 2,
where I2 denotes 2 $$ \times $$ 2 identity matrix and tr(A) denotes the sum of the diagonal entries of A. Then :
(P) If A $$ \ne $$ I2 , then |A| = –1
(Q) If |A| = 1, then tr(A) = 2,
where I2 denotes 2 $$ \times $$ 2 identity matrix and tr(A) denotes the sum of the diagonal entries of A. Then :
7
The sum of the first three terms of a G.P. is S and
their product is 27. Then all such S lie in :
8
If the letters of the word 'MOTHER' be permuted
and all the words so formed (with or without
meaning) be listed as in a dictionary, then the
position of the word 'MOTHER' is ______.
9
If $$\mathop {\lim }\limits_{x \to 1} {{x + {x^2} + {x^3} + ... + {x^n} - n} \over {x - 1}}$$ = 820,
(n $$ \in $$ N) then the value of n is equal to _______.
(n $$ \in $$ N) then the value of n is equal to _______.
10
Let $$\overrightarrow a $$, $$\overrightarrow b $$ and $$\overrightarrow c $$ be three unit vectors such that
$${\left| {\overrightarrow a - \overrightarrow b } \right|^2}$$ + $${\left| {\overrightarrow a - \overrightarrow c } \right|^2}$$ = 8.
Then $${\left| {\overrightarrow a + 2\overrightarrow b } \right|^2}$$ + $${\left| {\overrightarrow a + 2\overrightarrow c } \right|^2}$$ is equal to ______.
$${\left| {\overrightarrow a - \overrightarrow b } \right|^2}$$ + $${\left| {\overrightarrow a - \overrightarrow c } \right|^2}$$ = 8.
Then $${\left| {\overrightarrow a + 2\overrightarrow b } \right|^2}$$ + $${\left| {\overrightarrow a + 2\overrightarrow c } \right|^2}$$ is equal to ______.
11
The integral $$\int\limits_0^2 {\left| {\left| {x - 1} \right| - x} \right|dx} $$
is equal to______.
is equal to______.
12
If p(x) be a polynomial of degree three that has
a local maximum value 8 at x = 1 and a local
minimum value 4 at x = 2; then p(0) is equal to :
13
The value of
$${\left( {{{1 + \sin {{2\pi } \over 9} + i\cos {{2\pi } \over 9}} \over {1 + \sin {{2\pi } \over 9} - i\cos {{2\pi } \over 9}}}} \right)^3}$$ is :
$${\left( {{{1 + \sin {{2\pi } \over 9} + i\cos {{2\pi } \over 9}} \over {1 + \sin {{2\pi } \over 9} - i\cos {{2\pi } \over 9}}}} \right)^3}$$ is :
14
The domain of the function
f(x) = $${\sin ^{ - 1}}\left( {{{\left| x \right| + 5} \over {{x^2} + 1}}} \right)$$ is (– $$\infty $$, -a]$$ \cup $$[a, $$\infty $$). Then a is equal to :
f(x) = $${\sin ^{ - 1}}\left( {{{\left| x \right| + 5} \over {{x^2} + 1}}} \right)$$ is (– $$\infty $$, -a]$$ \cup $$[a, $$\infty $$). Then a is equal to :
15
Let
$$\alpha $$ and
$$\beta $$ be the roots of the equation
5x2 + 6x – 2 = 0. If Sn = $$\alpha $$n + $$\beta $$n, n = 1, 2, 3...., then :
5x2 + 6x – 2 = 0. If Sn = $$\alpha $$n + $$\beta $$n, n = 1, 2, 3...., then :
16
If R = {(x, y) : x, y
$$ \in $$ Z, x2 + 3y2
$$ \le $$ 8} is a relation
on the set of integers Z, then the domain of R–1 is :
17
Let X = {x
$$ \in $$ N : 1
$$ \le $$ x
$$ \le $$ 17} and
Y = {ax + b: x $$ \in $$ X and a, b $$ \in $$ R, a > 0}. If mean
and variance of elements of Y are 17 and 216
respectively then a + b is equal to :
Y = {ax + b: x $$ \in $$ X and a, b $$ \in $$ R, a > 0}. If mean
and variance of elements of Y are 17 and 216
respectively then a + b is equal to :
18
Let y = y(x) be the solution of the differential
equation,
$${{2 + \sin x} \over {y + 1}}.{{dy} \over {dx}} = - \cos x$$, y > 0,y(0) = 1.
If y($$\pi $$) = a and $${{dy} \over {dx}}$$ at x = $$\pi $$ is b, then the ordered pair (a, b) is equal to :
$${{2 + \sin x} \over {y + 1}}.{{dy} \over {dx}} = - \cos x$$, y > 0,y(0) = 1.
If y($$\pi $$) = a and $${{dy} \over {dx}}$$ at x = $$\pi $$ is b, then the ordered pair (a, b) is equal to :
Physics
1
In a reactor, 2 kg of 92U235 fuel is fully used up
in 30 days. The energy released per fission is
200 MeV. Given that the Avogadro number,
N = 6.023 $$ \times $$ 1026 per kilo mole and 1 eV =
1.6 × 10–19 J. The power output of the reactor is
close to
2
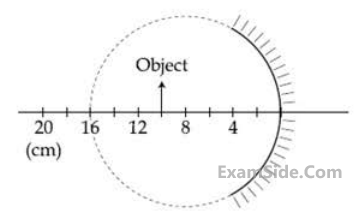 A spherical mirror is obtained as shown in the
figure from a hollow glass sphere. If an object
is positioned in front of the mirror, what will be
the nature and magnification of the image of
the object?
A spherical mirror is obtained as shown in the
figure from a hollow glass sphere. If an object
is positioned in front of the mirror, what will be
the nature and magnification of the image of
the object? (Figure drawn as schematic and not to scale)
3
Consider four conducting materials copper,
tungsten, mercury and aluminium with
resistivity $$\rho $$C, $$\rho $$T, $$\rho $$M and $$\rho $$A respectively. Then :
4
A particle of mass m with an initial velocity $$u\widehat i$$
collides perfectly elastically with a mass 3 m at
rest. It moves with a velocity $$v\widehat j$$ after collision,
then, v is given by :
5
A gas mixture consists of 3 moles of oxygen
and 5 moles of argon at temperature T.
Assuming the gases to be ideal and the oxygen
bond to be rigid, the total internal energy (in
units of RT) of the mixture is :
6
Train A and train B are running on parallel
tracks in the opposite directions with speeds of
36 km/hour and 72 km/hour, respectively. A
person is walking in train A in the direction
opposite to its motion with a speed of 1.8 km/
hour. Speed (in ms–1) of this person as
observed from train B will be close to :
(take the distance between the tracks as negligible)
(take the distance between the tracks as negligible)
7
The least count of the main scale of a vernier
callipers is 1 mm. Its vernier scale is divided
into 10 divisions and coincide with 9 divisions
of the main scale. When jaws are touching
each other, the 7th division of vernier scale
coincides with a division of main scale and the
zero of vernier scale is lying right side of the
zero of main scale. When this vernier is used to
measure length of a cylinder the zero of the
vernier scale between 3.1 cm and 3.2 cm and
4th VSD coincides with a main scale division.
The length of the cylinder is : (VSD is vernier
scale division)
8
If speed V, area A and force F are chosen as
fundamental units, then the dimension of
Young’s modulus will be
9
The mass density of a spherical galaxy varies
as
$${K \over r}$$ over a large distance ‘r’ from its centre.
In that region, a small star is in a circular orbit
of radius R. Then the period of revolution, T
depends on R as :
10
When radiation of wavelength $$\lambda $$ is used to
illuminate a metallic surface, the stopping
potential is V. When the same surface is
illuminated with radiation of wavelength 3$$\lambda $$,
the stopping potential is
$${V \over 4}$$. If the threshold
wavelength for the metallic surface is n$$\lambda $$ then
value of n will be __________.
11
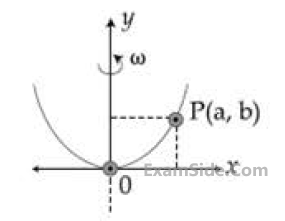
A bead of mass m stays at point P(a, b) on a
wire bent in the shape of a parabola y = 4Cx2
and rotating with angular speed $$\omega $$ (see figure).
The value of $$\omega $$ is (neglect friction) :

12
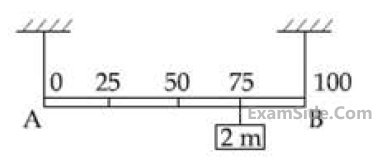
Shown in the figure is rigid and uniform one meter long rod AB held in horizontal position by two strings tied to its ends and attached to the ceiling. The rod is of mass ‘m’ and has another weight of mass 2 m hung at a distance of 75 cm from A. The tension in the string at A is :
13
Two identical strings X and Z made of same
material have tension TX and TZ in them. If their
fundamental frequencies are 450 Hz and
300 Hz, respectively, then the ratio TX/TZ is
14
A uniform cylinder of mass M and radius R is to
be pulled over a step of height a (a < R) by
applying a force F at its centre ‘O’
perpendicular to the plane through the axes of
the cylinder on the edge of the step (see
figure). The minimum value of F required is :
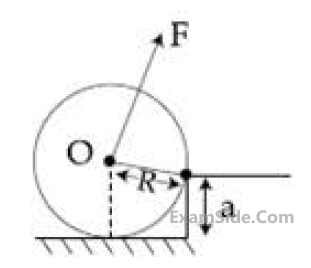

15
A plane electromagnetic wave, has
frequency of 2.0 $$ \times $$ 1010 Hz and its energy density is 1.02 $$ \times $$ 10–8 J/m3 in vacuum. The amplitude of the magnetic field of the wave is close to
( $${1 \over {4\pi {\varepsilon _0}}} = 9 \times {10^9}{{N{m^2}} \over {{C^2}}}$$ and speed of light
= 3 $$ \times $$ 108 ms–1)
frequency of 2.0 $$ \times $$ 1010 Hz and its energy density is 1.02 $$ \times $$ 10–8 J/m3 in vacuum. The amplitude of the magnetic field of the wave is close to
( $${1 \over {4\pi {\varepsilon _0}}} = 9 \times {10^9}{{N{m^2}} \over {{C^2}}}$$ and speed of light
= 3 $$ \times $$ 108 ms–1)
16
A charged particle (mass m and charge q)
moves along X-axis with velocity V0. When it
passes through the origin it enters a region having uniform electric field
$$\overrightarrow E = - E\widehat j$$ which extends upto x = d.
Equation of path of electron in the region x > d is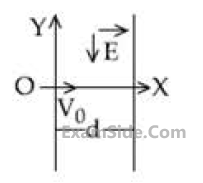
moves along X-axis with velocity V0. When it
passes through the origin it enters a region having uniform electric field
$$\overrightarrow E = - E\widehat j$$ which extends upto x = d.
Equation of path of electron in the region x > d is

17
A cylindrical vessel containing a liquid is
rotated about its axis so that the liquid rises at
its sides as shown in the figure. The radius of
vessel is 5 cm and the angular speed of
rotation is $$\omega $$ rad s–1. The difference in the
height, h (in cm) of liquid at the centre of
vessel and at the side will be :
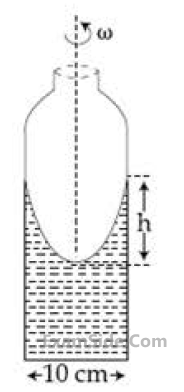

18
Interference fringes are observed on a screen
by illuminating two thin slits 1 mm apart with a
light source ($$\lambda $$ = 632.8 nm). The distance
between the screen and the slits is 100 cm. If
a bright fringe is observed on a screen at a
distance of 1.27 mm from the central bright
fringe, then the path difference between the
waves, which are reaching this point from the
slits is close is
19
A 5 $$\mu $$F capacitor is charged fully by a 220 V
supply. It is then disconnected from the supply
and is connected in series to another
uncharged 2.5 $$\mu $$F capacitor. If the energy
change during the charge redistribution is
$${X \over {100}}J$$ then value of X to the nearest integer is
_____.
20
A circular coil of radius 10 cm is placed in a
uniform magnetic field of 3.0 $$ \times $$ 10–5 T with its
plane perpendicular to the field initially. It is
rotated at constant angular speed about an
axis along the diameter of coil and
perpendicular to magnetic field so that it
undergoes half of rotation in 0.2 s. The
maximum value of EMF induced (in $$\mu $$V) in the
coil will be close to the integer _______.
21
An engine takes in 5 moles of air at 20oC and
1 atm, and compresses it adiabatically to
1/10th of the original volume. Assuming air to
be a diatomic ideal gas made up of rigid
molecules, the change in its internal energy
during this process comes out to be X kJ. The
value of X to the nearest integer is________.
22
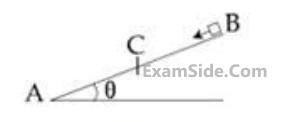
A small block starts slipping down from a point B on an inclined plane AB, which is making an angle $$\theta $$ with the horizontal section BC is smooth and the remaining section CA is rough with a coefficient of friction $$\mu $$. It is found that the block comes to rest as it reaches the bottom (point A) of the inclined plane. If BC = 2AC, the coefficient of friction is given by $$\mu $$ = ktan $$\theta $$ . The value of k is _________.
23
A beam of protons with speed 4 × 105 ms–1
enters a uniform magnetic field of 0.3 T at an
angle of 60° to the magnetic field. The pitch of
the resulting helical path of protons is close to :
(Mass of the proton = 1.67 $$ \times $$ 10–27 kg, charge
of the proton = 1.69 $$ \times $$ 10–19 C)
(Mass of the proton = 1.67 $$ \times $$ 10–27 kg, charge
of the proton = 1.69 $$ \times $$ 10–19 C)