JEE Main 2019 (Online) 12th April Evening Slot
Paper was held on
Fri, Apr 12, 2019 9:30 AM
Chemistry
1
In which one of the following equilibria, Kp $$ \ne $$ KC ?
2
Benzene diazonium chloride on reaction with aniline in the presence of dilute hydrochloric acid gives :
3
The molar solubility of Cd(OH)2 is 1.84 × 10–5
M in water. The expected solubility of Cd(OH)2 in a buffer
solution of pH = 12 is :
4
Which one of the following is likely to give a precipitate with AgNO3 solution ?
5
The compound used in the treatment of lead poisoning is :
6
In comparison to boron, berylium has :
7
Consider the following reactions :
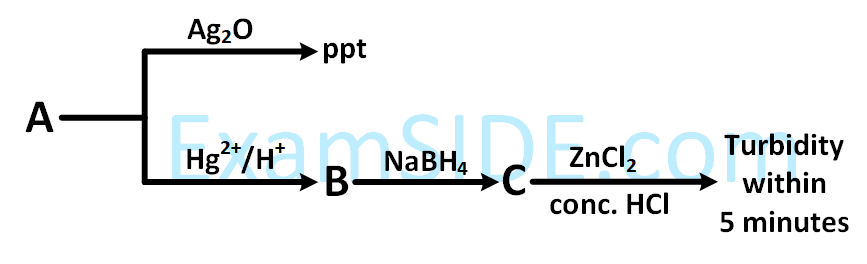
'A' is :

'A' is :
8
A solution is prepared by dissolving 0.6 g of urea (molar mass = 60 g mol–1) and 1.8 g of glucose (molar
mass = 180 g mol–1) in 100 mL of water at 27oC. The osmotic pressure of the solution is :
(R = 0.08206 L atm K–1 mol–1)
(R = 0.08206 L atm K–1 mol–1)
9
Heating of 2-chloro-1-phenylbutane with EtOK/EtOH gives X as the major product. Reaction of X with
Hg(OAc)2/H2O followed by NaBH4 gives Y as the major product. Y is :
10
NO2 required for a reaction is produced by the decomposition of N2O5 in CCl4 as per the equation,
2N2O5(g) $$ \to $$ 4NO2(g) + O2(g).
The initial concentration of N2O5 is 3.00 mol L–1 and it is 2.75 mol L–1 after 30 minutes. The rate of formation of NO2 is :
2N2O5(g) $$ \to $$ 4NO2(g) + O2(g).
The initial concentration of N2O5 is 3.00 mol L–1 and it is 2.75 mol L–1 after 30 minutes. The rate of formation of NO2 is :
11
Which of the given statements is INCORRECT about glycogen?
12
The pair that has similar atomic radii is :
13
The INCORRECT match in the following is :
14
Thermal decomposition of a Mn compound (X) at 513 K results in compound Y, MnO2 and gaseous product.
MnO2 reacts with NaCl and concentrated H2O4 to give a pungent gas Z. X, Y and Z, respectively, are :
15
The coordination numbers of Co and Al in [Co(Cl)(en)2]Cl and K3[Al(C2O4)3], respectively, are :
(en = ethane-1, 2-diamine)
16
25 g of an unknown hydrocarbon upon burning produces 88 g of CO2 and 9 g of H2O. This unknown
hydrocarbon contains :
17
The decreasing order of electrical conductivity of the following aqueous solutions is :
0.1 M Formic acid (A),
0.1 M Acetic acid (B),
0.1 M Benzoic acid (C)
0.1 M Formic acid (A),
0.1 M Acetic acid (B),
0.1 M Benzoic acid (C)
18
What will be the major product when m-cresol is reacted with propargyl bromide (HC$$ \equiv $$C–CH2Br) in
presence of K2CO3 in acetone?
19
Among the following, the energy of 2s orbital is lowest in :
20
The IUPAC name for the following compound is :
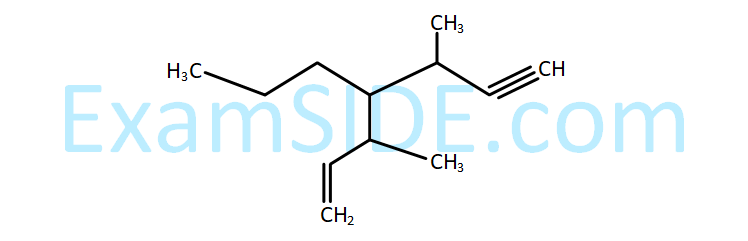

21
An 'Assertion' and a 'Reason' are given below. Choose the correct answer from the following options :
Assertion (A) : Vinyl halides do not undergo nucleophilic substitution easily.
Reason (R) : Even though the intermediate carbocation is stabilized by loosely held p-electrons, the cleavage is difficult because of strong bonding.
Assertion (A) : Vinyl halides do not undergo nucleophilic substitution easily.
Reason (R) : Even though the intermediate carbocation is stabilized by loosely held p-electrons, the cleavage is difficult because of strong bonding.
22
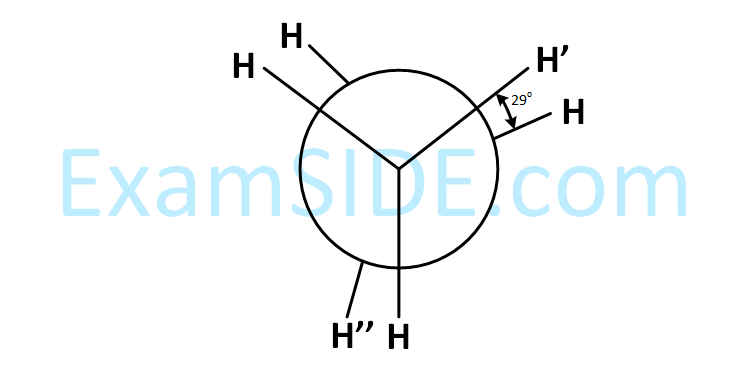
In the following skew conformation of ethane, H'–C–C–H'' dihedral angle is :

Mathematics
1
Let A, B and C be sets such that $$\phi $$ $$ \ne $$ A $$ \cap $$ B $$ \subseteq $$ C. Then which of the following statements is not true ?
2
If the area (in sq. units) bounded by the parabola y2
= 4$$\lambda $$x and the line y = $$\lambda $$x, $$\lambda $$ > 0, is $${1 \over 9}$$
, then $$\lambda $$ is equal to :
3
The general solution of the differential equation (y2
– x3)dx – xydy = 0 (x $$ \ne $$ 0) is :
(where c is a constant of integration)
4
Let $$a \in \left( {0,{\pi \over 2}} \right)$$ be fixed. If the integral
$$\int {{{\tan x + \tan \alpha } \over {\tan x - \tan \alpha }}} dx$$ = A(x) cos 2$$\alpha $$ + B(x) sin 2$$\alpha $$ + C, where C is a
constant of integration, then the functions A(x) and B(x) are respectively :
$$\int {{{\tan x + \tan \alpha } \over {\tan x - \tan \alpha }}} dx$$ = A(x) cos 2$$\alpha $$ + B(x) sin 2$$\alpha $$ + C, where C is a
constant of integration, then the functions A(x) and B(x) are respectively :
5
If $$\alpha $$, $$\beta $$ and $$\gamma $$ are three consecutive terms of a non-constant G.P. such that the equations $$\alpha $$x
2
+ 2$$\beta $$x + $$\gamma $$ = 0 and
x2
+ x – 1 = 0 have a common root, then $$\alpha $$($$\beta $$ + $$\gamma $$) is equal to :
6
A straight line L at a distance of 4 units from the origin makes positive intercepts on the coordinate axes and
the perpendicular from the origin to this line makes an angle of 60o with the line x + y = 0. Then an equation
of the line L is :
7
The term independent of x in the expansion of
$$\left( {{1 \over {60}} - {{{x^8}} \over {81}}} \right).{\left( {2{x^2} - {3 \over {{x^2}}}} \right)^6}$$ is equal to :
$$\left( {{1 \over {60}} - {{{x^8}} \over {81}}} \right).{\left( {2{x^2} - {3 \over {{x^2}}}} \right)^6}$$ is equal to :
8
If a1, a2, a3, ..... are in A.P. such that a1 + a7 + a16 = 40, then the sum of the first 15 terms of this A.P. is :
9
Let f(x) = 5 – |x – 2| and g(x) = |x + 1|, x $$ \in $$ R. If f(x) attains maximum value at $$\alpha $$ and g(x) attains
minimum value at $$\beta $$, then
$$\mathop {\lim }\limits_{x \to -\alpha \beta } {{\left( {x - 1} \right)\left( {{x^2} - 5x + 6} \right)} \over {{x^2} - 6x + 8}}$$ is equal to :
10
Let z $$ \in $$ C with Im(z) = 10 and it satisfies $${{2z - n} \over {2z + n}}$$ = 2i - 1 for some natural number n. Then :
11
A value of $$\theta \in \left( {0,{\pi \over 3}} \right)$$, for which
$$\left| {\matrix{ {1 + {{\cos }^2}\theta } & {{{\sin }^2}\theta } & {4\cos 6\theta } \cr {{{\cos }^2}\theta } & {1 + {{\sin }^2}\theta } & {4\cos 6\theta } \cr {{{\cos }^2}\theta } & {{{\sin }^2}\theta } & {1 + 4\cos 6\theta } \cr } } \right| = 0$$, is :
$$\left| {\matrix{ {1 + {{\cos }^2}\theta } & {{{\sin }^2}\theta } & {4\cos 6\theta } \cr {{{\cos }^2}\theta } & {1 + {{\sin }^2}\theta } & {4\cos 6\theta } \cr {{{\cos }^2}\theta } & {{{\sin }^2}\theta } & {1 + 4\cos 6\theta } \cr } } \right| = 0$$, is :
12
$$\mathop {\lim }\limits_{x \to 0} {{x + 2\sin x} \over {\sqrt {{x^2} + 2\sin x + 1} - \sqrt {{{\sin }^2}x - x + 1} }}$$ is :
13
The derivative of $${\tan ^{ - 1}}\left( {{{\sin x - \cos x} \over {\sin x + \cos x}}} \right)$$, with respect to $${x \over 2}$$
, where $$\left( {x \in \left( {0,{\pi \over 2}} \right)} \right)$$ is :
14
A value of $$\alpha $$ such that
$$\int\limits_\alpha ^{\alpha + 1} {{{dx} \over {\left( {x + \alpha } \right)\left( {x + \alpha + 1} \right)}}} = {\log _e}\left( {{9 \over 8}} \right)$$ is :
$$\int\limits_\alpha ^{\alpha + 1} {{{dx} \over {\left( {x + \alpha } \right)\left( {x + \alpha + 1} \right)}}} = {\log _e}\left( {{9 \over 8}} \right)$$ is :
15
An ellipse, with foci at (0, 2) and (0, –2) and minor axis of length 4, passes through which of the following points?
16
A group of students comprises of 5 boys and n girls. If the number of ways, in which a team of 3 students can
randomly be selected from this group such that there is at least one boy and at least one girl in each team, is
1750, then n is equal to :
17
A person throws two fair dice. He wins Rs. 15 for throwing a doublet (same numbers on the two dice), wins
Rs. 12 when the throw results in the sum of 9, and loses Rs. 6 for any other outcome on the throw. Then the
expected gain/loss (in Rs.) of the person is :
18
A circle touching the x-axis at (3, 0) and making an intercept of length 8 on the y-axis passes through the
point :
Physics
1
The electron in a hydrogen atom first jumps from the third excited state to the second excited state and
subsequently to the first excited state. The ratio of the respective wavelengths, $${{{\lambda _1}} \over {{\lambda _2}}}$$, of the photons emitted
in this process is :
2
A small speaker delivers 2 W of audio output. At what distance from the speaker will one detect 120 dB
intensity sound ? [Given reference intensity of sound as 10–12 W/m2
]
3
A tuning fork of frequency 480 Hz is used in an experiment for measuring speed of sound (v) in air
by resonance tube method. Resonance is observed to occur at two successive lengths of the air column,
l1 = 30 cm and l2 = 70 cm. Then, v is equal to -
4
An electron, moving along the x-axis with an initial energy of 100 eV, enters a region of magnetic field $$\overrightarrow B = \left( {1.5 \times {{10}^{ - 3}}T} \right)\widehat k$$
at S (See figure). The field extends between x = 0 and x = 2 cm. The electron is
detected at the point Q on a screen placed 8 cm away from the point S. The distance d between P and Q (on
the screen) is :
(electron’s charge = 1.6 × 10–19 C, mass of electron = 9.1 × 10–31 kg)
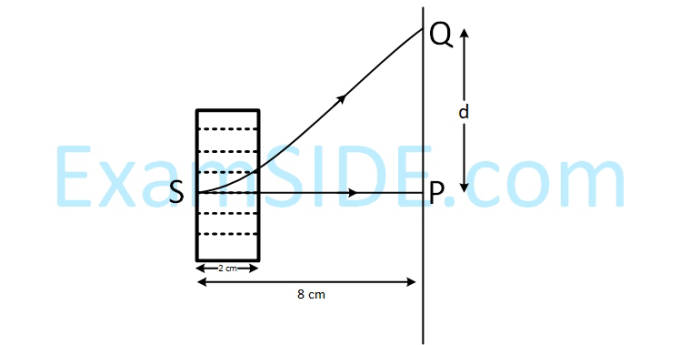

5
The number density of molecules of a gas depends on their distance r from the origin as, $$n\left( r \right) = {n_0}{e^{ - \alpha {r^4}}}$$.
Then the total number of molecules is proportional to :
6
A solid sphere, of radius R acquires a terminal velocity v1 when falling (due to gravity) through a viscous
fluid having a coefficient of viscosity . The sphere is broken into 27 identical solid spheres. If each of these
spheres acquires a terminal velocity, v2, when falling through the same fluid, the ratio (v1/v2) equals :
7
A moving coil galvanometer, having a resistance G, produces full scale deflection when a current Ig flows
through it. This galvanometer can be converted into (i) an ammeter of range 0 to I0(I0 > Ig) by connecting a
shunt resistance RA to it and (ii) into a voltmeter of range 0 to V (V = GI0) by connecting a series resistance
RV to it. Then,
8
A block of mass 5 kg is (i) pushed in case (A) and (ii) pulled in case (B), by a force F = 20 N, making an
angle of 30o with the horizontal, as shown in the figures. The coefficient of friction between the block and
floor is $$\mu $$ = 0.2. The difference between the accelerations of the blocks, in case (B) and case (A) will be :
(g = 10 ms–2)
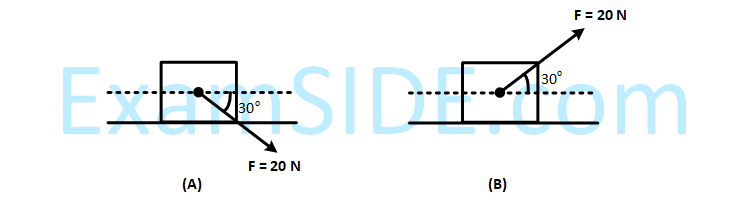

9
A plane electromagnetic wave having a frequency v = 23.9 GHz propagates along the positive z-direction in
free space. The peak value of the Electric Field is 60 V/m. Which among the following is the acceptable
magnetic field component in the electromagnetic wave ?
10
A diatomic gas with rigid molecules does 10 J of work when expanded at constant pressure. What would be
the heat energy absorbed by the gas, in this process ?
11
A uniform cylindrical rod of length L and radius r, is made from a material whose Young’s modulus of
Elasticity equals Y. When this rod is heated by temperature T and simultaneously subjected to a net
longitudinal compressional force F, its length remains unchanged. The coefficient of volume expansion, of
the material of the rod, is (nearly) equal to :
12
A smooth wire of length 2$$\pi $$r is bent into a circle and kept in a vertical plane. A bead can slide smoothly on
the wire. When the circle is rotating with angular speed $$\omega $$ about the vertical diameter AB, as shown in figure,
the bead is at rest with respect to the circular ring at position P as shown. Then the value of $$\omega $$2
is equal to -
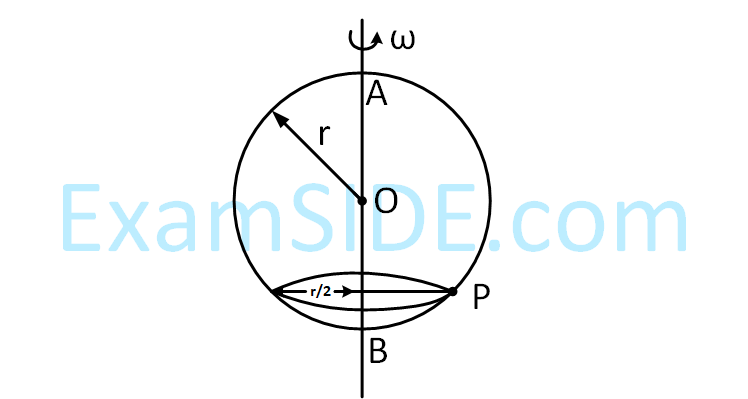

13
A system of three polarizers P1, P2, P3 is set up such that the pass axis of P3 is crossed with respect to that of P1.
The pass axis of P2 is inclined at 60o to the pass axis of P3. When a beam of unpolarized light of intensity I0 is
incident on P1, the intensity of light transmitted by the three polarizers is I. The ratio ($${{{I_0}} \over I}$$) equals (nearly) :
14
Let a total charge 2Q be distributed in a sphere of radius R, with the charge density given by $$\rho $$(r) = kr, where
r is the distance from the centre. Two charges A and B, of –Q each, are placed on diametrically opposite
points, at equal distance, $$a$$ from the centre. If A and B do not experience any force, then :
15
Consider the LR circuit shown in the figure. If the switch S is closed at t = 0 then the amount of charge that
passes through the battery between t = 0 and t = $${L \over R}$$
is :
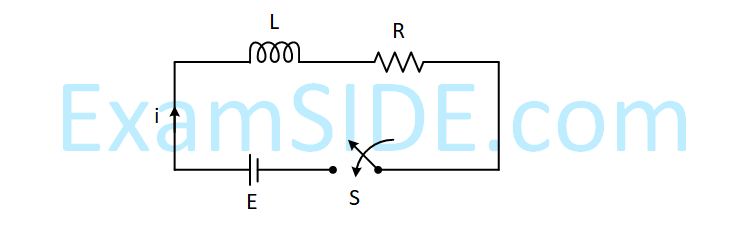

16
Consider an electron in a hydrogen atom revolving in its second excited state (having radius 4.65 $$\mathop A\limits^o $$). The
de-Broglie wavelength of this electron is :
17
One kg of water, at 20oC, heated in an electric kettle whose heating element has a mean (temperature
averaged) resistance of 20 $$\Omega $$. The rms voltage in the mains is 200 V. Ignoring heat loss from the kettle, time
taken for water to evaporate fully, is close to :
[Specific heat of water = 4200 J/(kg oC), Latent heat of water = 2260 kJ/kg]
18
A transparent cube of side, made of a material of refractive index $$\mu $$2, is immersed in a liquid of refractive
index $$\mu $$1($$\mu $$1 < $$\mu $$2). A ray is incident on the face AB at an angle $$\theta $$(shown in the figure). Total internal
reflection takes place at point E on the face BC.
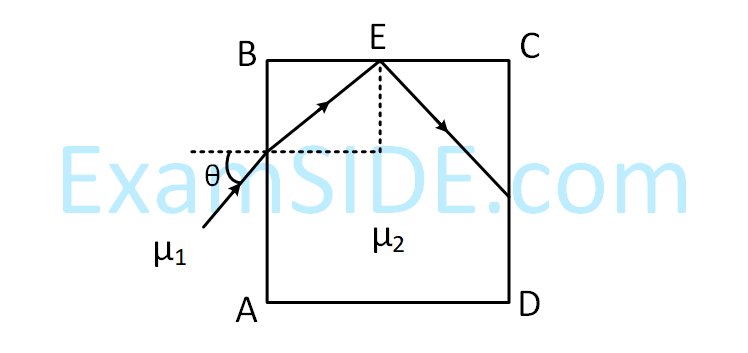
Then $$\theta $$ must satisfy :

Then $$\theta $$ must satisfy :
19
A particle is moving with speed v = b$$\sqrt x $$ along positive x-axis. Calculate the speed of the particle at
time t = $$\tau $$(assume that the particle is at origin t = 0)
20
In the given circuit, the charge on 4 $$\mu $$F capacitor will be :


21
Figure shows a DC voltage regulator circuit, with a Zener diode of breakdown voltage = 6V. If the
unregulated input voltage varies between 10 V to 16 V, then what is maximum Zener current?
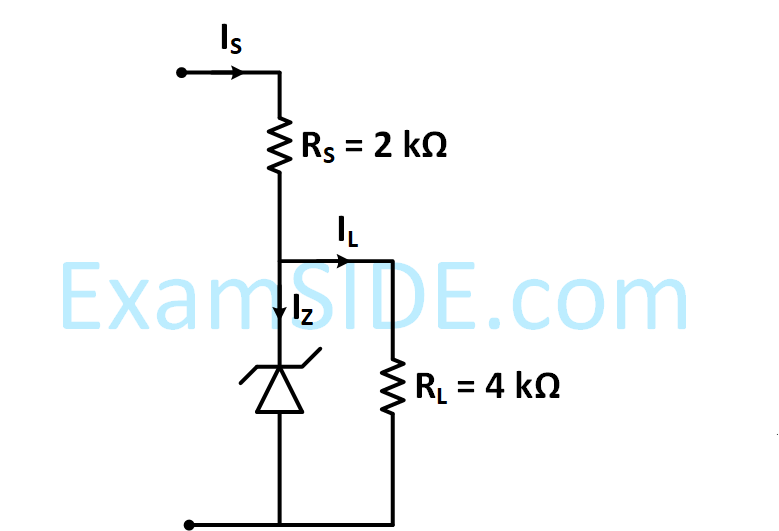

22
Two particles are projected from the same point with the same speed u such that they have the same range R,
but different maximum heights, h1 and h2. Which of the following is correct ?
23
Three particles of masses 50 g, 100 g and 150 g are placed at the vertices of an equilateral triangle of side
1 m (as shown in the figure). The (x, y) coordinates of the centre of mass will be :
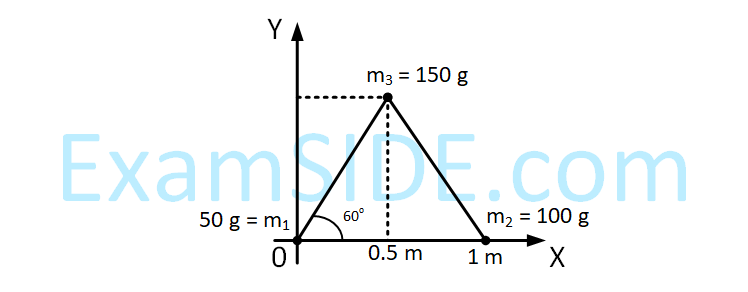

24
The ratio of the weights of a body on the Earth’s surface to that on the surface of a planets is 9 : 4. The mass
of the planet is
$${1 \over 9}$$
th of that of the Earth. If 'R' is the radius of the Earth, what is the radius of the planet ?
(Take the planets to have the same mass density)
25
A spring whose unstretched length is l has a force constant k. The spring is cut into two pieces of unstretched
lengths l1 and l2 where, l1 = nl2 and n is an integer. The ratio k1/k2 of the corresponding force constant, k1 and
k2 will be :
26
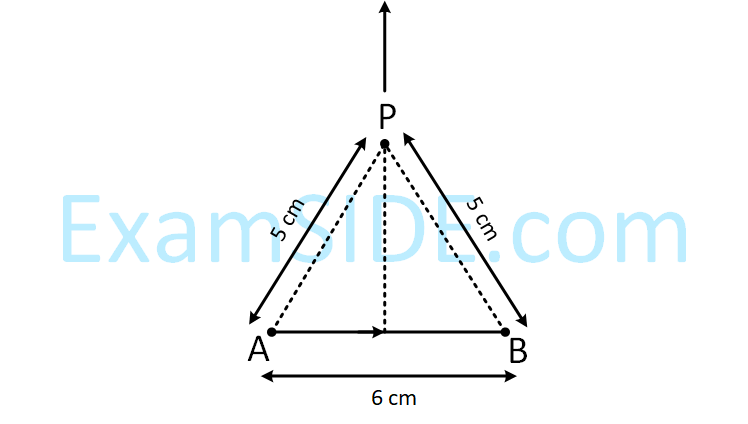
Find the magnetic field at point P due to a straight line segment AB of length 6 cm carrying a current of 5A.
(See figure) ($$\mu $$0 = 4$$\pi $$ × 10–7 N-A–2)