During water-gas shift reaction

The complex with highest magnitude of crystal field splitting energy $\left(\Delta_{0}\right)$ is :

The major product formed in the Friedel-Craft acylation of chlorobenzene is

The number of $\mathrm{P}-\mathrm{O}-\mathrm{P}$ bonds in $\mathrm{H}_{4} \mathrm{P}_{2} \mathrm{O}_{7},\left(\mathrm{HPO}_{3}\right)_{3}$ and $\mathrm{P}_{4} \mathrm{O}_{10}$ are respectively :

Which of the following statement is correct for paper chromatography?

Which is not true for arginine?

Consider the following sequence of reactions:


The product ' $\mathrm{B}$ ' is

Given below are two statements:

Statement I : According to Bohr's model of hydrogen atom, the angular momentum of an electron in a given stationary state is quantised.

Statement II : The concept of electron in Bohr's orbit, violates the Heisenberg uncertainty principle.

In the light of the above statements, choose the most appropriate answer from the options given below:

Which of the following statement(s) is/are correct?

(A) The $\mathrm{pH}$ of $1 \times 10^{-8}~ \mathrm{M} ~\mathrm{HCl}$ solution is 8 .

(B) The conjugate base of $\mathrm{H}_{2} \mathrm{PO}_{4}^{-}$ is $\mathrm{HPO}_{4}^{2-}$.

(C) $\mathrm{K}_{\mathrm{w}}$ increases with increase in temperature.

(D) When a solution of a weak monoprotic acid is titrated against a strong base at half neutralisation point, $\mathrm{pH}=\frac{1}{2} \mathrm{pK}_{\mathrm{a}}$

Choose the correct answer from the options given below:

Consider the following statements:

(A) NF₃ molecule has a trigonal planar structure.

(B) Bond length of $\mathrm{N}_{2}$ is shorter than $\mathrm{O}_{2}$.

(C) Isoelectronic molecules or ions have identical bond order.

(D) Dipole moment of $\mathrm{H}_{2}\mathrm{S}$ is higher than that of water molecule.

Choose the correct answer from the options given below:

In the above conversion the correct sequence of reagents to be added is

'A' formed in the above reaction is

The product formed in the following multistep reaction is :

Decreasing order of reactivity towards electrophilic substitution for the following compounds is :

For a reversible reaction $\mathrm{A} \rightleftharpoons \mathrm{B}$, the $\Delta \mathrm{H}_{\text{forward reaction}} = 20 \mathrm{~kJ} \mathrm{~mol}^{-1}$. The activation energy of the uncatalysed forward reaction is $300 \mathrm{~kJ} \mathrm{~mol}^{-1}$. When the reaction is catalysed keeping the reactant concentration same, the rate of the catalysed forward reaction at $27^{\circ} \mathrm{C}$ is found to be same as that of the uncatalysed reaction at $327^{\circ} \mathrm{C}$.

The activation energy of the catalysed backward reaction is ___________ $\mathrm{kJ}~ \mathrm{mol}^{-1}$.

The volume (in $\mathrm{mL}$) of $0.1 \mathrm{M} ~\mathrm{AgNO}_{3}$ required for complete precipitation of chloride ions present in $20 \mathrm{~mL}$ of $0.01 \mathrm{M}$ solution of $\left[\mathrm{Cr}\left(\mathrm{H}_{2} \mathrm{O}\right)_{5} \mathrm{Cl}\right] \mathrm{Cl}_{2}$ as silver chloride is __________.

The number of correct statements from the following is _______.

(A) Conductivity always decreases with decrease in concentration for both strong and weak electrolytes.

(B) The number of ions per unit volume that carry current in a solution increases on dilution.

(C) Molar conductivity increases with decrease in concentration

(D) The variation in molar conductivity is different for strong and weak electrolytes

(E) For weak electrolytes, the change in molar conductivity with dilution is due to decrease in degree of dissociation.

In Chromyl chloride, the oxidation state of chromium is $(+)$ _______________.

The vapour pressure of $30 \%(\mathrm{w} / \mathrm{v})$ aqueous solution of glucose is __________ $\mathrm{mm} ~\mathrm{Hg}$ at $25^{\circ} \mathrm{C}$.

[Given : The density of $30 \%$ (w/v), aqueous solution of glucose is $1.2 \mathrm{~g} \mathrm{~cm}^{-3}$ and vapour pressure of pure water is $24 \mathrm{~mm}~ \mathrm{Hg}$.]

(Molar mass of glucose is $180 \mathrm{~g} \mathrm{~mol}^{-1}$.)

$30.4 \mathrm{~kJ}$ of heat is required to melt one mole of sodium chloride and the entropy change at the melting point is $28.4 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}$ at 1 atm. The melting point of sodium chloride is _______________ K (Nearest Integer)

The total change in the oxidation state of manganese involved in the reaction of $\mathrm{KMnO}_{4}$ and potassium iodide in the acidic medium is ____________.

The homoleptic and octahedral complex of $\mathrm{Co}^{2+}$ and $\mathrm{H}_{2} \mathrm{O}$ has ___________ unpaired electron(s) in the $t_{2\mathrm{g}}$ set of orbitals.

The total number of isoelectronic species from the given set is ___________.

$\mathrm{O}^{2-}, \mathrm{F}^{-}, \mathrm{Al}, \mathrm{Mg}^{2+}, \mathrm{Na}^{+}, \mathrm{O}^{+}, \mathrm{Mg}, \mathrm{Al}^{3+}, \mathrm{F}$

Let $x=x(y)$ be the solution of the differential equation

$2(y+2) \log _{e}(y+2) d x+\left(x+4-2 \log _{e}(y+2)\right) d y=0, y>-1$

with $x\left(e^{4}-2\right)=1$. Then $x\left(e^{9}-2\right)$ is equal to :

If $\int\limits_{0}^{1} \frac{1}{\left(5+2 x-2 x^{2}\right)\left(1+e^{(2-4 x)}\right)} d x=\frac{1}{\alpha} \log _{e}\left(\frac{\alpha+1}{\beta}\right), \alpha, \beta>0$, then $\alpha^{4}-\beta^{4}$ is equal to :

The total number of three-digit numbers, divisible by 3, which can be formed using the digits $1,3,5,8$, if repetition of digits is allowed, is :

Let $\mathrm{ABCD}$ be a quadrilateral. If $\mathrm{E}$ and $\mathrm{F}$ are the mid points of the diagonals $\mathrm{AC}$ and $\mathrm{BD}$ respectively and $(\overrightarrow{A B}-\overrightarrow{B C})+(\overrightarrow{A D}-\overrightarrow{D C})=k \overrightarrow{F E}$, then $k$ is equal to :

If the domain of the function

$f(x)=\log _{e}\left(4 x^{2}+11 x+6\right)+\sin ^{-1}(4 x+3)+\cos ^{-1}\left(\frac{10 x+6}{3}\right)$ is $(\alpha, \beta]$, then

$36|\alpha+\beta|$ is equal to :

Let $[x]$ denote the greatest integer function and

$f(x)=\max \{1+x+[x], 2+x, x+2[x]\}, 0 \leq x \leq 2$. Let $m$ be the number of

points in $[0,2]$, where $f$ is not continuous and $n$ be the number of points in

$(0,2)$, where $f$ is not differentiable. Then $(m+n)^{2}+2$ is equal to :

The mean and standard deviation of 10 observations are 20 and 8 respectively. Later on, it was observed that one observation was recorded as 50 instead of 40. Then the correct variance is :

Let $\left(a+b x+c x^{2}\right)^{10}=\sum\limits_{i=0}^{20} p_{i} x^{i}, a, b, c \in \mathbb{N}$.

If $p_{1}=20$ and $p_{2}=210$, then $2(a+b+c)$ is equal to :

A bag contains 6 white and 4 black balls. A die is rolled once and the number of balls equal to the number obtained on the die are drawn from the bag at random. The probability that all the balls drawn are white is :

The number of real roots of the equation $x|x|-5|x+2|+6=0$, is :

If $(\alpha, \beta)$ is the orthocenter of the triangle $\mathrm{ABC}$ with vertices $A(3,-7), B(-1,2)$ and $C(4,5)$, then $9 \alpha-6 \beta+60$ is equal to :

Let $A_{1}$ and $A_{2}$ be two arithmetic means and $G_{1}, G_{2}, G_{3}$ be three geometric

means of two distinct positive numbers. Then $G_{1}^{4}+G_{2}^{4}+G_{3}^{4}+G_{1}^{2} G_{3}^{2}$ is equal to :

Let $\mathrm{S}$ be the set of all values of $\lambda$, for which the shortest distance between

the lines $\frac{x-\lambda}{0}=\frac{y-3}{4}=\frac{z+6}{1}$ and $\frac{x+\lambda}{3}=\frac{y}{-4}=\frac{z-6}{0}$ is 13. Then $8\left|\sum\limits_{\lambda \in S} \lambda\right|$ is equal to :

If the set $\left\{\operatorname{Re}\left(\frac{z-\bar{z}+z \bar{z}}{2-3 z+5 \bar{z}}\right): z \in \mathbb{C}, \operatorname{Re}(z)=3\right\}$ is equal to

the interval $(\alpha, \beta]$, then $24(\beta-\alpha)$ is equal to :

A person forgets his 4-digit ATM pin code. But he remembers that in the code all the digits are different, the greatest digit is 7 and the sum of the first two digits is equal to the sum of the last two digits. Then the maximum number of trials necessary to obtain the correct code is ___________.

Let an ellipse with centre $(1,0)$ and latus rectum of length $\frac{1}{2}$ have its major axis along $\mathrm{x}$-axis. If its minor axis subtends an angle $60^{\circ}$ at the foci, then the square of the sum of the lengths of its minor and major axes is equal to ____________.

If the area bounded by the curve $2 y^{2}=3 x$, lines $x+y=3, y=0$ and outside the circle $(x-3)^{2}+y^{2}=2$ is $\mathrm{A}$, then $4(\pi+4 A)$ is equal to ____________.

Let $f(x)=\int \frac{d x}{\left(3+4 x^{2}\right) \sqrt{4-3 x^{2}}},|x|<\frac{2}{\sqrt{3}}$. If $f(0)=0$

and $f(1)=\frac{1}{\alpha \beta} \tan ^{-1}\left(\frac{\alpha}{\beta}\right)$, $\alpha, \beta>0$, then $\alpha^{2}+\beta^{2}$ is equal to ____________.

Consider the triangles with vertices $A(2,1), B(0,0)$ and $C(t, 4), t \in[0,4]$.

If the maximum and the minimum perimeters of such triangles are obtained at

$t=\alpha$ and $t=\beta$ respectively, then $6 \alpha+21 \beta$ is equal to ___________.

The number of elements in the set

$\left\{n \in \mathbb{N}: 10 \leq n \leq 100\right.$ and $3^{n}-3$ is a multiple of 7$\}$ is ___________.

Let $A=\{1,2,3,4\}$ and $\mathrm{R}$ be a relation on the set $A \times A$ defined by

$R=\{((a, b),(c, d)): 2 a+3 b=4 c+5 d\}$. Then the number of elements in $\mathrm{R}$ is ____________.

A wire of length ' $L$ ' and radius ' $r$ ' is clamped rigidly at one end. When the other end of the wire is pulled by a force $f$, its length increases by ' $l$ '. Another wire of same material of length ' $2 \mathrm{~L}$ ' and radius ' $2 r$ ' is pulled by a force ' $2 f$ '. Then the increase in its length will be :

The position of a particle related to time is given by $x=\left(5 t^{2}-4 t+5\right) \mathrm{m}$. The magnitude of velocity of the particle at $t=2 s$ will be :

The electric field due to a short electric dipole at a large distance $(r)$ from center of dipole on the equatorial plane varies with distance as :

In the given circuit, the current (I) through the battery will be

The de Broglie wavelength of an electron having kinetic energy $\mathrm{E}$ is $\lambda$. If the kinetic energy of electron becomes $\frac{E}{4}$, then its de-Broglie wavelength will be :

In a linear Simple Harmonic Motion (SHM)

(A) Restoring force is directly proportional to the displacement.

(B) The acceleration and displacement are opposite in direction.

(C) The velocity is maximum at mean position.

(D) The acceleration is minimum at extreme points.

Choose the correct answer from the options given below:

Two identical particles each of mass ' $m$ ' go round a circle of radius $a$ under the action of their mutual gravitational attraction. The angular speed of each particle will be :

A single slit of width $a$ is illuminated by a monochromatic light of wavelength $600 \mathrm{~nm}$. The value of ' $a$ ' for which first minimum appears at $\theta=30^{\circ}$ on the screen will be :

The position vector of a particle related to time $t$ is given by

$\vec{r}=\left(10 t \hat{i}+15 t^{2} \hat{j}+7 \hat{k}\right) m$

The direction of net force experienced by the particle is :

A body is released from a height equal to the radius $(\mathrm{R})$ of the earth. The velocity of the body when it strikes the surface of the earth will be

(Given $g=$ acceleration due to gravity on the earth.)

A vector in $x-y$ plane makes an angle of $30^{\circ}$ with $y$-axis. The magnitude of $\mathrm{y}$-component of vector is $2 \sqrt{3}$. The magnitude of $x$-component of the vector will be :

The speed of a wave produced in water is given by $v=\lambda^{a} g^{b} \rho^{c}$. Where $\lambda, g$ and $\rho$ are wavelength of wave, acceleration due to gravity and density of water respectively. The values of $a, b$ and $c$ respectively, are :

For designing a voltmeter of range $50 \mathrm{~V}$ and an ammeter of range $10 \mathrm{~mA}$ using a galvanometer which has a coil of resistance $54 \Omega$ showing a full scale deflection for $1 \mathrm{~mA}$ as in figure.



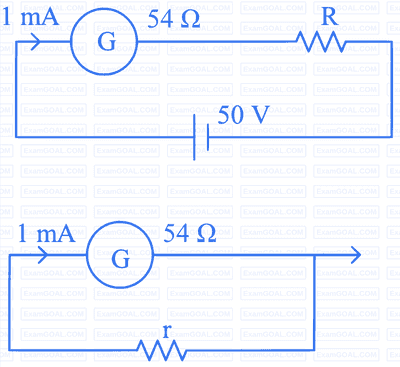
(A) for voltmeter $R \approx 50 \mathrm{k} \Omega$

(B) for ammeter $\mathrm{r} \approx 0.2 \Omega$

(C) for ammeter $\mathrm{r}=6 \Omega$

(D) for voltmeter $R \approx 5 \mathrm{k} \Omega$

(E) for voltmeter $R \approx 500 \Omega$

Choose the correct answer from the options given below:

A thermodynamic system is taken through cyclic process. The total work done in the process is :

Given below are two statements:

Statement I : The equivalent resistance of resistors in a series combination is smaller than least resistance used in the combination.

Statement II : The resistivity of the material is independent of temperature.

In the light of the above statements, choose the correct answer from the options given below :

Match List I with List II of Electromagnetic waves with corresponding wavelength range :

List I	List II
(A) Microwave	(I) $400 \mathrm{~nm}$ to $1 \mathrm{~nm}$
(B) Ultraviolet	(II) $1 \mathrm{~nm}$ to $10^{-3} \mathrm{~nm}$
(C) X-Ray	(III) $1 \mathrm{~mm}$ to $700 \mathrm{~nm}$
(D) Infra-red	(IV) $0.1 \mathrm{~m}$ to $1 \mathrm{~mm}$

Choose the correct answer from the options given below:

A flask contains Hydrogen and Argon in the ratio $2: 1$ by mass. The temperature of the mixture is $30^{\circ} \mathrm{C}$. The ratio of average kinetic energy per molecule of the two gases ( $\mathrm{K}$ argon/K hydrogen) is :

(Given: Atomic Weight of $\mathrm{Ar}=39.9$ )

$12 \mathrm{~V}$ battery connected to a coil of resistance $6 \Omega$ through a switch, drives a constant current in the circuit. The switch is opened in $1 \mathrm{~ms}$. The emf induced across the coil is $20 \mathrm{~V}$. The inductance of the coil is :

An electron in a hydrogen atom revolves around its nucleus with a speed of $6.76 \times 10^6 \mathrm{~ms}^{-1}$ in an orbit of radius $0.52 \mathrm{~A}^{\circ}$. The magnetic field produced at the nucleus of the hydrogen atom is _________ T.

The fundamental frequency of vibration of a string stretched between two rigid support is $50 \mathrm{~Hz}$. The mass of the string is $18 \mathrm{~g}$ and its linear mass density is $20 \mathrm{~g} / \mathrm{m}$. The speed of the transverse waves so produced in the string is ___________ $\mathrm{ms}^{-1}$

In the given figure the total charge stored in the combination of capacitors is $100~ \mu \mathrm{C}$. The value of ' $x$ ' is _________.

As per given figure $A, B$ and $C$ are the first, second and third excited energy levels of hydrogen atom respectively. If the ratio of the two wavelengths $\left(\right.$ i.e. $\left.\frac{\lambda_{1}}{\lambda_{2}}\right)$ is $\frac{7}{4 n}$, then the value of $n$ will be __________.

The refractive index of a transparent liquid filled in an equilateral hollow prism is $\sqrt{2}$. The angle of minimum deviation for the liquid will be ___________ $$^\circ$$.

A block of mass $10 \mathrm{~kg}$ is moving along $\mathrm{x}$-axis under the action of force $F=5 x~ N$. The work done by the force in moving the block from $x=2 m$ to $4 m$ will be __________ J.

A network of four resistances is connected to $9 \mathrm{~V}$ battery, as shown in figure. The magnitude of voltage difference between the points $\mathrm{A}$ and $\mathrm{B}$ is __________ $V$.

A $20 \mathrm{~cm}$ long metallic rod is rotated with $210~ \mathrm{rpm}$ about an axis normal to the rod passing through its one end. The other end of the rod is in contact with a circular metallic ring. A constant and uniform magnetic field $0.2 \mathrm{~T}$ parallel to the axis exists everywhere. The emf developed between the centre and the ring is ____________ $\mathrm{mV}$.

Take $\pi=\frac{22}{7}$

There is an air bubble of radius $1.0 \mathrm{~mm}$ in a liquid of surface tension $0.075~ \mathrm{Nm}^{-1}$ and density $1000 \mathrm{~kg} \mathrm{~m}^{-3}$ at a depth of $10 \mathrm{~cm}$ below the free surface. The amount by which the pressure inside the bubble is greater than the atmospheric pressure is _________ $\mathrm{Pa}\left(\mathrm{g}=10 \mathrm{~ms}^{-2}\right)$

A solid sphere and a solid cylinder of same mass and radius are rolling on a horizontal surface without slipping. The ratio of their radius of gyrations respectively $\left(k_{\text {sph }}: k_{\text {cyl }}\right)$ is $2: \sqrt{x}$. The value of $x$ is ____________ .