JEE Main 2019 (Online) 9th April Morning Slot
Paper was held on
Tue, Apr 9, 2019 3:30 AM
Chemistry
1
The major product of the following reaction is :


2
The major product of the following reaction is :
$${\rm{C}}{{\rm{H}}_3}{\rm{CH = CHC}}{{\rm{O}}_2}{\rm{CH_3 }}\buildrel {LiAl{H_4}} \over \longrightarrow $$
$${\rm{C}}{{\rm{H}}_3}{\rm{CH = CHC}}{{\rm{O}}_2}{\rm{CH_3 }}\buildrel {LiAl{H_4}} \over \longrightarrow $$
3
The increasing order of reactivity of the
following compounds towards aromatic
electrophilic substitution reaction is :


4
The major product of the following reaction is :


5
The standard Gibbs energy for the given cell
reaction in kJ mol–1 at 298 K is :
Zn(s) + Cu2+ (aq) $$ \to $$ Zn2+ (aq) + Cu (s),
E° = 2 V at 298 K
(Faraday's constant, F = 96000 C mol–1)
Zn(s) + Cu2+ (aq) $$ \to $$ Zn2+ (aq) + Cu (s),
E° = 2 V at 298 K
(Faraday's constant, F = 96000 C mol–1)
6
Among the following, the set of parameters that
represents path function, is :
(A) q + w
(B) q
(C) w
(D) H–TS
(A) q + w
(B) q
(C) w
(D) H–TS
7
The osmotic pressure of a dilute solution of an
ionic compound XY in water is four times that
of a solution of 0.01 M BaCl2 in water.
Assuming complete dissociation of the given
ionic compounds in water, the concentration of
XY (in mol L–1) in solution is :
8
The correct IUPAC name of the following
compound is :


9
The given plots represent the variation of the
concentration of a reactant R with time for two
different reactions (i) and (ii). The respective
orders of the reactions are :


10
For a reaction,
N2(g) + 3H2(g) $$ \to $$ 2NH3(g) ;
identify dihydrogen (H2) as a limiting reagent in the following reaction mixtures.
N2(g) + 3H2(g) $$ \to $$ 2NH3(g) ;
identify dihydrogen (H2) as a limiting reagent in the following reaction mixtures.
11
The one that will show optical activity is :
(en = ethane-1,2-diamine)
(en = ethane-1,2-diamine)
12
Among the following, the molecule expected
to be stabilized by anion formation is :
C2, O2, NO, F2
C2, O2, NO, F2
13
Which of the following statements is not true
about sucrose?
14
The organic compound that gives following
qualitative analysis is :
| Test | Inference | |
|---|---|---|
| (a) | Dil. HCl | Insoluble |
| (b) | NaOH solution | soluble |
| (c) | Br2/water | Decolourization |
15
The major product of the following reaction is :


16
The degenerate orbitals of [Cr(H2O)6]3+ are :
17
The correct order of the oxidation states of
nitrogen in NO, N2O, NO2 and N2O3 is :
18
The major product of the following reaction is :


19
For any given series of spectral lines of atomic
hydrogen, let $$\Delta \mathop v\limits^\_ = $$ $$\Delta {\overline v _{\max }} - \Delta {\overline v _{\min }}$$ be the difference
in maximum and minimum frequencies in
cm–1. The ratio Lyman Balmer $${{\Delta {{\overline v }_{Lyman}}} \over {\Delta {{\overline v }_{Balmer}}}}$$ is :
20
The element having greatest difference between
its first and second ionization energies, is :
21
Aniline dissolved in dilute HCl is reacted with
sodium nitrite at 0ºC. This solution was added
dropwise to a solution containing equimolar
mixture of aniline and phenol in dil. HCl. The
structure of the major product is
22
Liquid 'M' and liquid 'N' form an ideal solution.
The vapour pressures of pure liquids 'M' and
'N' are 450 and 700 mmHg, respectively, at the
same temperature. Then correct statement is:
(xM = Mole fraction of 'M' in solution ;
xN = Mole fraction of 'N' in solution ;
yM = Mole fraction of 'M' in vapour phase ;
yN = Mole fraction of 'N' in vapour phase)
(xM = Mole fraction of 'M' in solution ;
xN = Mole fraction of 'N' in solution ;
yM = Mole fraction of 'M' in vapour phase ;
yN = Mole fraction of 'N' in vapour phase)
Mathematics
1
If the standard deviation of the numbers
–1, 0, 1, k is $$\sqrt 5$$ where k > 0, then k is equal to
2
Let p, q $$ \in $$ R. If 2 - $$\sqrt 3$$ is a root of the quadratic
equation, x2 + px + q = 0, then :
3
Let ƒ(x) = 15 – |x – 10|; x $$ \in $$ R. Then the set
of all values of x, at which the function,
g(x) = ƒ(ƒ(x)) is not differentiable, is :
4
If ƒ(x) is a non-zero polynomial of degree four,
having local extreme points at x = –1, 0, 1; then
the set
S = {x $$ \in $$ R : ƒ(x) = ƒ(0)}
Contains exactly :
S = {x $$ \in $$ R : ƒ(x) = ƒ(0)}
Contains exactly :
5
The value of $$\int\limits_0^{\pi /2} {{{{{\sin }^3}x} \over {\sin x + \cos x}}dx} $$ is
6
Let $$\overrightarrow \alpha = 3\widehat i + \widehat j$$ and $$\overrightarrow \beta = 2\widehat i - \widehat j + 3 \widehat k$$
. If $$\overrightarrow \beta = {\overrightarrow \beta _1} - \overrightarrow {{\beta _2}} $$,
where $${\overrightarrow \beta _1}$$
is parallel to $$\overrightarrow \alpha $$ and $$\overrightarrow {{\beta _2}} $$
is perpendicular
to $$\overrightarrow \alpha $$ , then $${\overrightarrow \beta _1} \times \overrightarrow {{\beta _2}} $$
is equal to
7
All the points in the set
$$S = \left\{ {{{\alpha + i} \over {\alpha - i}}:\alpha \in R} \right\}(i = \sqrt { - 1} )$$ lie on a :
$$S = \left\{ {{{\alpha + i} \over {\alpha - i}}:\alpha \in R} \right\}(i = \sqrt { - 1} )$$ lie on a :
8
If $$\left[ {\matrix{
1 & 1 \cr
0 & 1 \cr
} } \right]\left[ {\matrix{
1 & 2 \cr
0 & 1 \cr
} } \right]$$$$\left[ {\matrix{
1 & 3 \cr
0 & 1 \cr
} } \right]$$....$$\left[ {\matrix{
1 & {n - 1} \cr
0 & 1 \cr
} } \right] = \left[ {\matrix{
1 & {78} \cr
0 & 1 \cr
} } \right]$$,
then the inverse of $$\left[ {\matrix{ 1 & n \cr 0 & 1 \cr } } \right]$$ is
then the inverse of $$\left[ {\matrix{ 1 & n \cr 0 & 1 \cr } } \right]$$ is
9
If the function ƒ : R – {1, –1} $$ \to $$ A defined by
ƒ(x) = $${{{x^2}} \over {1 - {x^2}}}$$ , is surjective, then A is equal to
ƒ(x) = $${{{x^2}} \over {1 - {x^2}}}$$ , is surjective, then A is equal to
10
If one end of a focal chord of the parabola,
y2 = 16x is at (1, 4), then the length of this focal
chord is :
11
If the function ƒ defined on , $$\left( {{\pi \over 6},{\pi \over 3}} \right)$$ by
$$$f(x) = \left\{ {\matrix{
{{{\sqrt 2 {\mathop{\rm cosx}\nolimits} - 1} \over {\cot x - 1}},} & {x \ne {\pi \over 4}} \cr
{k,} & {x = {\pi \over 4}} \cr
} } \right.$$$
is continuous, then
k is equal to
12
The value of cos210° – cos10°cos50° + cos250° is
13
Let $$\sum\limits_{k = 1}^{10} {f(a + k) = 16\left( {{2^{10}} - 1} \right)} $$ where the function
ƒ satisfies
ƒ(x + y) = ƒ(x)ƒ(y) for all natural numbers x, y and ƒ(1) = 2. then the natural number 'a' is
ƒ(x + y) = ƒ(x)ƒ(y) for all natural numbers x, y and ƒ(1) = 2. then the natural number 'a' is
14
Four persons can hit a target correctly with
probabilities
$${1 \over 2}$$, $${1 \over 3}$$, $${1 \over 4}$$ and
$${1 \over 8}$$ respectively. if all hit
at the target independently, then the probability that
the target would be hit, is :
15
Let $$\alpha $$ and $$\beta $$ be the roots of the equation
x2 + x + 1 = 0. Then for y $$ \ne $$ 0 in R,
$$$\left| {\matrix{ {y + 1} & \alpha & \beta \cr \alpha & {y + \beta } & 1 \cr \beta & 1 & {y + \alpha } \cr } } \right|$$$ is equal to
$$$\left| {\matrix{ {y + 1} & \alpha & \beta \cr \alpha & {y + \beta } & 1 \cr \beta & 1 & {y + \alpha } \cr } } \right|$$$ is equal to
16
The area (in sq. units) of the region
A = {(x, y) : x2 $$ \le $$ y $$ \le $$ x + 2} is
A = {(x, y) : x2 $$ \le $$ y $$ \le $$ x + 2} is
17
Let the sum of the first n terms of a non-constant
A.P., a1, a2, a3, ..... be $$50n + {{n(n - 7)} \over 2}A$$, where
A is a constant. If d is the common difference of
this A.P., then the ordered pair (d, a50) is equal to
18
The integral $$\int {{\rm{se}}{{\rm{c}}^{{\rm{2/ 3}}}}\,{\rm{x }}\,{\rm{cose}}{{\rm{c}}^{{\rm{4 / 3}}}}{\rm{x \,dx}}} $$ is equal to
(Hence C is a constant of integration)
19
The solution of the differential equation
$$x{{dy} \over {dx}} + 2y$$ = x2 (x $$ \ne $$ 0) with y(1) = 1, is :
$$x{{dy} \over {dx}} + 2y$$ = x2 (x $$ \ne $$ 0) with y(1) = 1, is :
20
If the fourth term in the binomial expansion of $${\left( {{2 \over x} + {x^{{{\log }_8}x}}} \right)^6}$$
(x > 0) is 20 × 87, then a value of
x is :
21
A committee of 11 members is to be formed from
8 males and 5 females. If m is the number of ways
the committee is formed with at least 6 males and
n is the number of ways the committee is formed
with at least 3 females, then :
22
Slope of a line passing through P(2, 3) and
intersecting the line, x + y = 7 at a distance of
4 units from P, is :
Physics
1
A concave mirror for face viewing has focal
length of 0.4 m. The distance at which you hold
the mirror from your face in order to see your
image upright with a magnification of 5 is :
2
For a given gas at 1 atm pressure, rms speed
of the molecule is 200 m/s at 127°C. At 2 atm
pressure and at 227°C, the rms speed of the
molecules will be :
3
A rectangular coil (Dimension 5 cm × 2.5 cm)
with 100 turns, carrying a current of 3 A in the
clock-wise direction is kept centered at the
origin and in the X-Z plane. A magnetic field
of 1 T is applied along X-axis. If the coil is tilted
through 45° about Z-axis, then the torque on
the coil is :
4
If 'M' is the mass of water that rises in a capillary
tube of radius 'r', then mass of water which will
rise in a capillary tube of radius '2r' is :
5
Taking the wavelength of first Balmer line in
hydrogen spectrum (n = 3 to n = 2) as 660 nm,
the wavelength of the 2nd Balmer line (n = 4 to
n = 2) will be :
6
The magnetic field of a plane electromagnetic
wave is given by :
$$$\overline B = {B_0}\widehat i\left[ {\cos (kz - \omega t)} \right] + {B_i}\widehat j\cos (kz + \omega t)$$$ B0 = 3 × 10–5 T and B1 = 2 × 10–6 T.
The rms value of the force experienced by a stationary charge Q = 10–4 C at z = 0 is closest to :
$$$\overline B = {B_0}\widehat i\left[ {\cos (kz - \omega t)} \right] + {B_i}\widehat j\cos (kz + \omega t)$$$ B0 = 3 × 10–5 T and B1 = 2 × 10–6 T.
The rms value of the force experienced by a stationary charge Q = 10–4 C at z = 0 is closest to :
7
A uniform cable of mass 'M' and length 'L' is
placed on a horizontal surface such that its (1/n)th
part is hanging below the edge of the
surface. To lift the hanging part of the cable upto
the surface, the work done should be :
8
A stationary horizontal disc is free to rotate
about its axis. When a torque is applied on it,
its kinetic energy as a function of $$\theta $$, where $$\theta $$
is the angle by which it has rotated, is given as
k$$\theta $$2. If its moment of inertia is I then the
angular acceleration of the disc is :
9
A string is clamped at both the ends and it is
vibrating in its 4th harmonic. The equation of the
stationary wave is Y = 0.3 sin(0.157x) cos(200pt).
The length of the string is : (All quantities are
in SI units.)
10
The following bodies are made to roll up
(without slipping) the same inclined plane from
a horizontal plane. : (i) a ring of radius R, (ii)
a solid cylinder of radius
R/2 and (iii) a solid
sphere of radius
R/4 . If in each case, the speed
of the centre of mass at the bottom of the incline
is same, the ratio of the maximum heights they
climb is :
11
A rigid square loop of side 'a' and carrying
current I2 is lying on a horizontal surface near
a long current I1 carrying wire in the same plane
as shown in figure. The net force on the loop
due to wire will be :
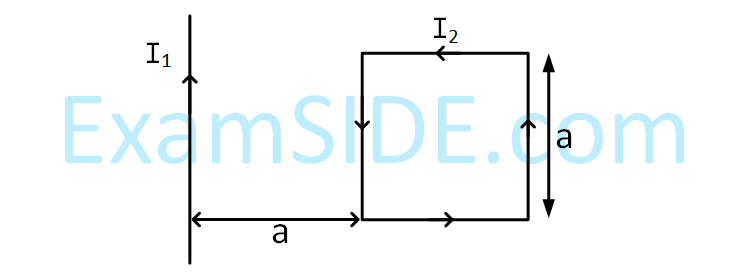

12
The figure shows a Young's double slit
experimental setup. It is observed that when a
thin transparent sheet of thickness t and
refractive index μ is put in front of one of the
slits, the central maximum gest shifted by a
distance equal to n fringe widths. If the
wavelength of light used is $$\lambda $$, t will be :


13
A capacitor with capacitance 5μF is charged to
5μC. If the plates are pulled apart to reduce the
capacitance to 2μF, how much work is done ?
14
A ball is thrown vertically up (taken as +z-axis)
from the ground. The correct momentum-height
(p-h) diagram is :
15
The total number of turns and cross-section area
in a solenoid is fixed. However, its length L is varied
by adjusting the separation between windings. The
inductance of solenoid will be proportional to :
16
The electric field of light wave is given as
$$$\overrightarrow E = {10^{ - 3}}\cos \left( {{{2\pi x} \over {5 \times {{10}^{ - 7}}}} - 2\pi \times 6 \times {{10}^{14}}t} \right)\mathop x\limits^ \wedge {{\rm N} \over C}$$$
This
light falls on a metal plate of work function
2eV. The stopping potential of the photoelectrons
is :
Given, E (in eV) = 12375/$$\lambda $$(inÅ)
Given, E (in eV) = 12375/$$\lambda $$(inÅ)
17
A moving coil galvanometer has resistance 50$$\Omega $$
and it indicates full deflection at 4mA current.
A voltmeter is made using this galvanometer
and a 5 k$$\Omega $$ resistance. The maximum voltage,
that can be measured using this voltmeter, will
be close to :
18
The pressure wave, P = 0.01 sin [1000t – 3x] Nm–2,
corresponds to the sound produced by a vibrating blade
on a day when atmospheric temperature is 0°C. On
some other day, when temperature is T, the speed of
sound produced by the same blade and at the same
frequency is found to be 336 ms–1 . Approximate value
of T is
19
A solid sphere of mass 'M' and radius 'a' is
surrounded by a uniform concentric spherical
shell of thickness 2a and mass 2M. The
gravitational field at distance '3a' from the
centre will be :
20
The stream of a river is flowing with a speed
of 2km/h. A swimmer can swim at a speed of
4km/h. What should be the direction of the
swimmer with respect to the flow of the river to
cross the river straight ?
21
A system of three charges are placed as shown
in the figure :
 If D >> d, the potential energy of the system is
best given by :
If D >> d, the potential energy of the system is
best given by :
 If D >> d, the potential energy of the system is
best given by :
If D >> d, the potential energy of the system is
best given by :
22
Determine the charge on the capacitor in the
following circuit :


23
A body of mass 2 kg makes an eleastic collision
with a second body at rest and continues to move
in the original direction but with one fourth of its
original speed. What is the mass of the second
body ?
24
A simple pendulum oscillating in air has period
T. The bob of the pendulum is completely
immersed in a non-viscous liquid. The density
of the liquid is
1/16 th of the material of the bob.
If the bob is inside liquid all the time, its period
of oscillation in this liquid is :
25
Following figure shows two processes A and
B for a gas. If $$\Delta $$QA and $$\Delta $$QB are the amount of
heat absorbed by the system in two cases, and
$$\Delta $$UA and $$\Delta $$UB are changes in internal energies,
respectively, then :
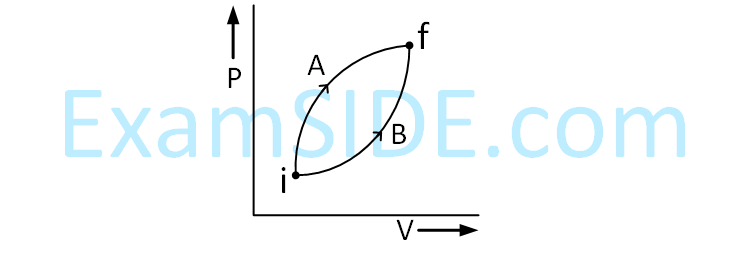

26
A wire of resistance R is bent to form a square
ABCD as shown in the figure. The effective
resistance between E and C is :
(E is mid-point of arm CD)


27
An HCl molecule has rotational, translational
and vibrational motions. If the rms velocity of
HCl molecules in its gaseous phase is $$\overline v $$ , m is
its mass and kB is Boltzmann constant, then its
temperature will be :
28
In the density measurement of a cube, the mass and
edge length are measured as (10.00 ± 0.10) kg and
(0.10 ± 0.01) m, respectively. The error in the
measurement of density is :