JEE Main 2017 (Online) 9th April Morning Slot
Paper was held on
Sun, Apr 9, 2017 3:30 AM
Chemistry
1
The increasing order of the boiling points for the following compounds is :


2
Which of the following compounds will show highest dipole moment ?


3
Among the following compounds, the increasing order of their basic strength is :


4
In the following reaction sequence :

The compound I is :

The compound I is :
5
The major product of the following reaction is :


6
In the following structure, the double bonds are marked as I, II, III and IV

Geometrical isomerism is not possible at site (s) :

Geometrical isomerism is not possible at site (s) :
7
Which of the following compounds is most reactive to an aqueous solution of sodium
carbonate ?
8
[Co2(CO)8] displays :
9
The incorrect statement among the following is :
10
A compound of molecular formula C8H8O2
reacts with acetophenone to form a single cross-aldol product in the presence
of base. The same compound on reaction with conc. NaOH forms benzyl alcohol as
one of the products. The structure of the compound is :
11
Which of the following ions does not liberate hydrogen gas on reaction with dilute acids ?
12
The group having triangular planar structures is :
13
A gas undergoes change from state A to state B. In this process, the heat absorbed
and work done by the gas is 5 J and 8 J, respectively. Now gas is brought back to
A by another process during which 3 J of heat is evolved. In this reverse process of
B to A :
14
Which one of the following is an oxide?
15
The following reaction occurs in the Blast Furnace where iron ore is reduced to iron
metal :
Fe2O3(s) + 3 CO(g) $$\rightleftharpoons$$ 2 Fe(1) + 3 CO2(g)
Using the Le Chatelier’s principle, predict which one of the following will not disturb the equilibrium ?
Fe2O3(s) + 3 CO(g) $$\rightleftharpoons$$ 2 Fe(1) + 3 CO2(g)
Using the Le Chatelier’s principle, predict which one of the following will not disturb the equilibrium ?
16
The electronic configuration with the highest ionization enthalpy is :
17
A solution is prepared by mixing 8.5 g of CH2Cl2 and 11.95 g of CHCl3 . If vapour pressure of CH2Cl2
and CHCl3 at 298 K are 415 and 200 mmHg respectively, the mole fraction of CHCl3 in vapour form is : (Molar mass of Cl = 35.5 g mol−1)
18
The rate of a reaction quadruples when the temperature changes from 300 to 310 K. The activation energy of this reaction is :
(Assume activation energy and preexponential factor are independent of temperature; ln 2 = 0.693; R = 8.314 J mol−1 K−1)
(Assume activation energy and preexponential factor are independent of temperature; ln 2 = 0.693; R = 8.314 J mol−1 K−1)
19
To find the standard potential of M3+/M electrode,the following cell is constituted : Pt/M/M3+(0.001 mol L−1 )/Ag+(0.01 mol L−1 )/Ag
The emf of the cell is found to be 0.421 volt at 298 K. The standard potential of half reaction M3+ + 3e−$$ \to $$ M at 298 K will be :
(Given $$E_{A{g^ + }\,/\,Ag}^ - $$ at 298 K = 0.80 Volt)
The emf of the cell is found to be 0.421 volt at 298 K. The standard potential of half reaction M3+ + 3e−$$ \to $$ M at 298 K will be :
(Given $$E_{A{g^ + }\,/\,Ag}^ - $$ at 298 K = 0.80 Volt)
20
What quantity (in mL) of a 45% acid solution of a mono-protic strong acid must
be mixed with a 20% solution of the same acid to produce 800 mL of a 29.875% acid
solution ?
21
The electron in the hydrogen atom undergoes transition from higher orbitals
to orbital of radius 211.6 pm. This transition is associated with :
22
50 mL of 0.2 M ammonia solution is treated with 25 mL of 0.2 M HCl. If pKb of ammonia solution is 4.75, the pH of the mixture will be :
23
An ideal gas undergoes isothermal expansion at constant pressure. During
the process :
Mathematics
1
If three positive numbers a, b and c are in A.P. such that abc = 8, then the minimum possible value of b is :
2
The number of ways in which 5 boys and 3 girls can be seated on a round table if a
particular boy B1 and a particular girl G1 never sit adjacent to each other, is :
3
The coefficient of x−5 in the binomial expansion of
$${\left( {{{x + 1} \over {{x^{{2 \over 3}}} - {x^{{1 \over 3}}} + 1}} - {{x - 1} \over {x - {x^{{1 \over 2}}}}}} \right)^{10}},$$ where x $$ \ne $$ 0, 1, is :
$${\left( {{{x + 1} \over {{x^{{2 \over 3}}} - {x^{{1 \over 3}}} + 1}} - {{x - 1} \over {x - {x^{{1 \over 2}}}}}} \right)^{10}},$$ where x $$ \ne $$ 0, 1, is :
4
For two 3 × 3 matrices A and B, let A + B = 2BT and 3A + 2B = I3, where BT is
the transpose of B and I3 is 3 × 3 identity matrix. Then :
5
The equation
Im $$\left( {{{iz - 2} \over {z - i}}} \right)$$ + 1 = 0, z $$ \in $$ C, z $$ \ne $$ i
represents a part of a circle having radius equal to :
Im $$\left( {{{iz - 2} \over {z - i}}} \right)$$ + 1 = 0, z $$ \in $$ C, z $$ \ne $$ i
represents a part of a circle having radius equal to :
6
The sum of all the real values of x satisfying the equation
2(x$$-$$1)(x2 + 5x $$-$$ 50) = 1 is :
2(x$$-$$1)(x2 + 5x $$-$$ 50) = 1 is :
7
The function f : N $$ \to $$ N defined by f (x) = x $$-$$ 5 $$\left[ {{x \over 5}} \right],$$ Where N is the set of natural numbers and [x] denotes the greatest integer less than or equal to x, is :
8
The two adjacent sides of a cyclic quadrilateral are 2 and 5 and the angle between them is 60o. If the area of the quadrilateral is $$4\sqrt 3 $$, then the perimeter
of the quadrilateral is :
9
A value of x satisfying the equation sin[cot−1 (1+ x)] = cos [tan−1 x], is :
10
Let E and F be two independent events. The probability that both E and F happen is $${1 \over {12}}$$ and the probability that neither E nor F happens is $${1 \over {2}}$$, then a value of $${{P\left( E \right)} \over {P\left( F \right)}}$$ is :
11
The sum of 100 observations and the sum of their squares are 400 and 2475,
respectively. Later on, three observations, 3, 4 and 5, were found to be incorrect. If
the incorrect observations are omitted, then the variance of the remaining observations
is :
12
If the vector $$\overrightarrow b = 3\widehat j + 4\widehat k$$ is written as the
sum of a vector $$\overrightarrow {{b_1}} ,$$ paralel to $$\overrightarrow a = \widehat i + \widehat j$$ and a vector $$\overrightarrow {{b_2}} ,$$ perpendicular to $$\overrightarrow a ,$$ then $$\overrightarrow {{b_1}} \times \overrightarrow {{b_2}} $$ is equal to :
13
From a group of 10 men and 5 women, four member committees are to be formed each of which must contain at least one woman. Then the probability for these committees to have more women than men, is :
14
The eccentricity of an ellipse having centre at the origin, axes along the co-ordinate
axes and passing through the points (4, −1) and (−2, 2) is :
15
If $$\int\limits_1^2 {{{dx} \over {{{\left( {{x^2} - 2x + 4} \right)}^{{3 \over 2}}}}}} = {k \over {k + 5}},$$ then k is equal to :
16
If 2x = y$${^{{1 \over 5}}}$$ + y$${^{ - {1 \over 5}}}$$ and
(x2 $$-$$ 1) $${{{d^2}y} \over {d{x^2}}}$$ + $$\lambda $$x $${{dy} \over {dx}}$$ + ky = 0,
then $$\lambda $$ + k is equal to :
(x2 $$-$$ 1) $${{{d^2}y} \over {d{x^2}}}$$ + $$\lambda $$x $${{dy} \over {dx}}$$ + ky = 0,
then $$\lambda $$ + k is equal to :
17
A line drawn through the point P(4, 7) cuts the circle x2 + y2 = 9 at the points A and B. Then PA⋅PB is equal to :
18
Let f be a polynomial function such that
f (3x) = f ' (x) . f '' (x), for all x $$ \in $$ R. Then :
f (3x) = f ' (x) . f '' (x), for all x $$ \in $$ R. Then :
19
A square, of each side 2, lies above the x-axis and has one vertex at the origin. If
one of the sides passing through the origin makes an angle 30o with the positive direction of the x-axis, then the sum of the x-coordinates of the vertices of the square is :
20
If $$\,\,\,$$ f$$\left( {{{3x - 4} \over {3x + 4}}} \right)$$ = x + 2, x $$ \ne $$ $$-$$ $${4 \over 3}$$, and
$$\int {} $$f(x) dx = A log$$\left| {} \right.$$1 $$-$$ x $$\left| {} \right.$$ + Bx + C,
then the ordered pair (A, B) is equal to :
(where C is a constant of integration)
$$\int {} $$f(x) dx = A log$$\left| {} \right.$$1 $$-$$ x $$\left| {} \right.$$ + Bx + C,
then the ordered pair (A, B) is equal to :
(where C is a constant of integration)
21
The function f defined by
f(x) = x3 $$-$$ 3x2 + 5x + 7 , is :
f(x) = x3 $$-$$ 3x2 + 5x + 7 , is :
22
The value of k for which the function
$$f\left( x \right) = \left\{ {\matrix{ {{{\left( {{4 \over 5}} \right)}^{{{\tan \,4x} \over {\tan \,5x}}}}\,\,,} & {0 < x < {\pi \over 2}} \cr {k + {2 \over 5}\,\,\,,} & {x = {\pi \over 2}} \cr } } \right.$$
is continuous at x = $${\pi \over 2},$$ is :
$$f\left( x \right) = \left\{ {\matrix{ {{{\left( {{4 \over 5}} \right)}^{{{\tan \,4x} \over {\tan \,5x}}}}\,\,,} & {0 < x < {\pi \over 2}} \cr {k + {2 \over 5}\,\,\,,} & {x = {\pi \over 2}} \cr } } \right.$$
is continuous at x = $${\pi \over 2},$$ is :
Physics
1
In an experiment a convex lens of focal length 15 cm is placed coaxially on an optical bench in front of a convex mirror at a distance of 5 cm from it. It is found that an object and its image coincide, if the object is placed at a distance of 20 cm from the lens. The focal length of the convex mirror is :
2
A circular hole of radius $${R \over 4}$$ is made in a thin uniform disc having mass M and radius R, as shown in figure. The moment of inertia of the remaining portion of the disc about an axis passing through the point O and perpendicular to the plane of the disc is :
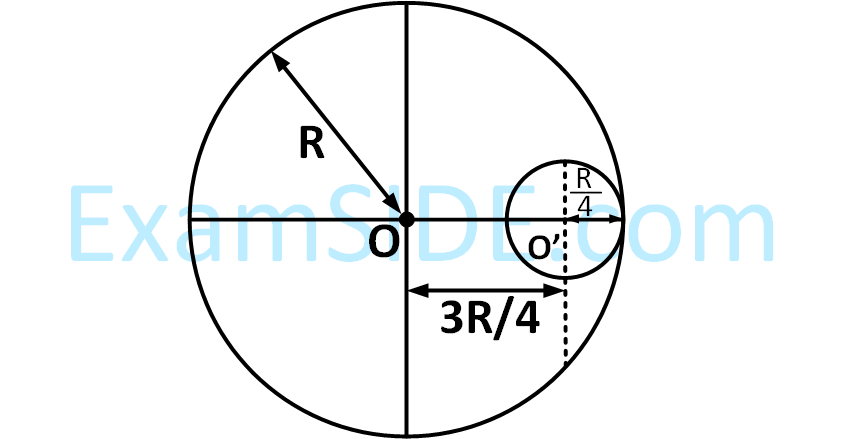

3
A conical pendulum of length 1 m makes an angle $$\theta $$ = 45o w.r.t. Z-axis and moves in a circle in the XY plane. The radius of the circle is 0.4 m and its center is vertically below O. The speed of the pendulum, in its circular path, will be: (Take g = 10 ms−2 )
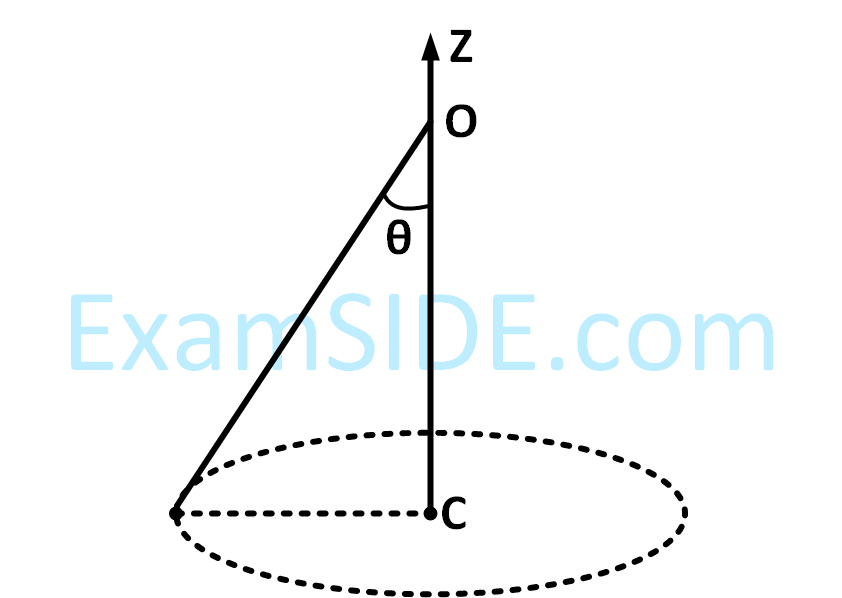

4
The machine as shown has 2 rods of length1 m connected by a pivot at the top. The end of one rod is connected to the floor by a stationary pivot and the end of the other rod has a roller that rolls along the floor in a slot. As the roller goes back and forth, a 2 kg weight moves up and down. If the roller is moving towards right at a constant speed, the weight moves up with a :
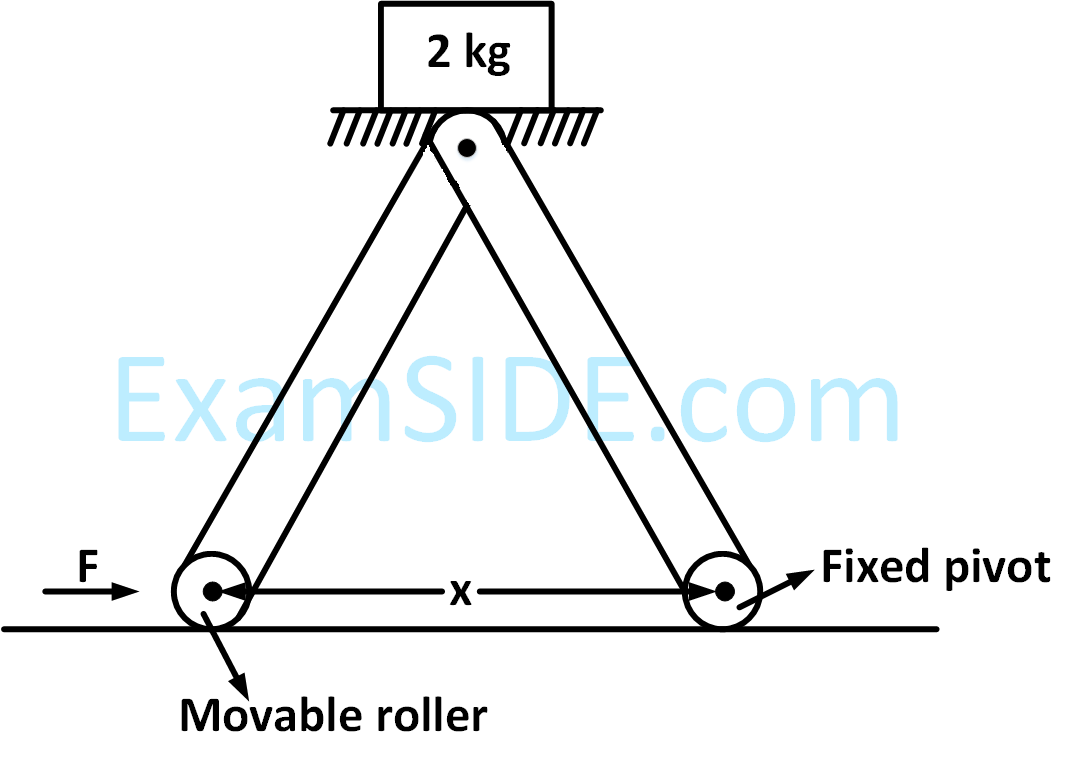

5
Two particles A and B of equal mass M are moving with the same speed $$\upsilon $$ as shown in the figure. They collide completely inelastically and move as a single particle C. The angle $$\theta $$ that the path of C makes with the X-axis is given by :


6
In an experiment to determine the period of a simple pendulum of length 1 m, it is attached to different spherical bobs of radii r1
and r2 . The two spherical bobs have uniform mass distribution. If the relative difference in the periods, is found to be
5×10−4 s, the difference in radii, $$\left| {} \right.$$r1 $$-$$ r2 $$\left| {} \right.$$ is best given by :
7
Imagine that a reactor converts all given mass into energy and that it operates at a power level of 109 watt. The mass of the fuel consumed per hour in the reactor will be : (velocity of light, c is
3×108 m/s)
8
The acceleration of an electron in the first orbit of the hydrogen atom (n = 1) is :
9
A Laser light of wavelength 660 nm is used to weld Retina detachment. If a Laser pulse of width 60 ms and power 0.5 kW is used the approximate number of photons in the pulse are :
[Take Planck's constant h $$=$$ 6.62 $$ \times $$ 10$$-$$34 Js]
[Take Planck's constant h $$=$$ 6.62 $$ \times $$ 10$$-$$34 Js]
10
A single slit of width 0.1 mm is illuminated by a parallel beam of light of wavelength 6000 $$\mathop A\limits^ \circ $$ and diffraction bands are observed on a screen 0.5 m from the slit. The distance of the third dark band from the central bright band is :
11
The mass density of a spherical body is given by
$$\rho $$ (r) = $${k \over r}$$ for r $$ \le $$ R and $$\rho $$ (r) = 0 for r > R,
where r is the distance from the centre.
The correct graph that describes qualitatively the acceleration, a, of a test particle as a function of r is :
$$\rho $$ (r) = $${k \over r}$$ for r $$ \le $$ R and $$\rho $$ (r) = 0 for r > R,
where r is the distance from the centre.
The correct graph that describes qualitatively the acceleration, a, of a test particle as a function of r is :
12
The electric field component of a monochromatic radiation is given by
$$\overrightarrow E $$ = 2 E0 $$\widehat i$$ cos kz cos $$\omega $$t
Its magnetic field $$\overrightarrow B $$ is then given by :
$$\overrightarrow E $$ = 2 E0 $$\widehat i$$ cos kz cos $$\omega $$t
Its magnetic field $$\overrightarrow B $$ is then given by :
13
A sinusoidal voltage of peak value 283 V and angular frequency 320/s is applied to a series LCR circuit. Given that R=5 $$\Omega $$, L=25 mH and C=1000 $$\mu $$F. The total impedance, and phase difference between the voltage across the source and the current will respectively be :
14
A negative test charge is moving near a long straight wire carrying a current. The force acting on the test charge is parallel to the direction of the current. The motion of the charge is :
15
A uniform wire of length 1 and radius r has a resistance of 100 $$\Omega $$. It is recast into a wire of radius $${r \over 2}.$$ The resistance of new wire will be :
16
A standing wave is formed by the superposition of two waves travelling in
opposite directions. The transverse displacement is given by
y(x, t) = 0.5 sin $$\left( {{{5\pi } \over 4}x} \right)\,$$ cos(200 $$\pi $$t).
What is the speed of the travelling wave moving in the positive x direction ?
(x and t are in meter and second, respectively.)
y(x, t) = 0.5 sin $$\left( {{{5\pi } \over 4}x} \right)\,$$ cos(200 $$\pi $$t).
What is the speed of the travelling wave moving in the positive x direction ?
(x and t are in meter and second, respectively.)
17
N moles of a diatomic gas in a cylinder are at a temperature T. Heat is supplied to the cylinder such that the temperature remains constant but n moles of the diatomic gas get converted into monoatomic gas. What is the change in the total kinetic energy of the gas ?
18
Two tubes of radii r1 and r2, and lengths l1 and l2 , respectively, are connected in series
and a liquid flows through each of them in stream line conditions. P1 and P2 are pressure differences across the two tubes.
If P2 is 4P1 and l2 is $${{{1_1}} \over 4}$$, then the radius r2 will be equal to :
If P2 is 4P1 and l2 is $${{{1_1}} \over 4}$$, then the radius r2 will be equal to :
19
A steel rail of length 5 m and area of cross section 40cm2
is prevented from expanding along its length while the temperature rises
by 10oC. If coefficient of linear expansion and Young’s modulus of steel are 1.2×10−5 K−1 and 2×1011 Nm−2 respectively, the force developed in the rail is approximately :
20
A car is standing 200 m behind a bus, which is also at rest. The two start moving at the same instant but with different forward accelerations. The bus has acceleration 2 m/s2 and the car has acceleration 4 m/s2 . The car will catch up with the bus after a time of :
21
A physical quantity P is described by the relation
P = a$$^{{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}$$ b2 c3 d$$-$$4
If the relative errors in the measurement of a, b, c and d respectively, are 2%, 1%, 3% and 5%, then the relative error in P will be :
P = a$$^{{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}$$ b2 c3 d$$-$$4
If the relative errors in the measurement of a, b, c and d respectively, are 2%, 1%, 3% and 5%, then the relative error in P will be :
22
The figure shows three circuits I, II and III which are connected to a 3V battery. If the powers dissipated by the configurations I, II and III are P1 , P2 and P3 respectively, then :


23
For the P-V diagram given for an ideal gas,
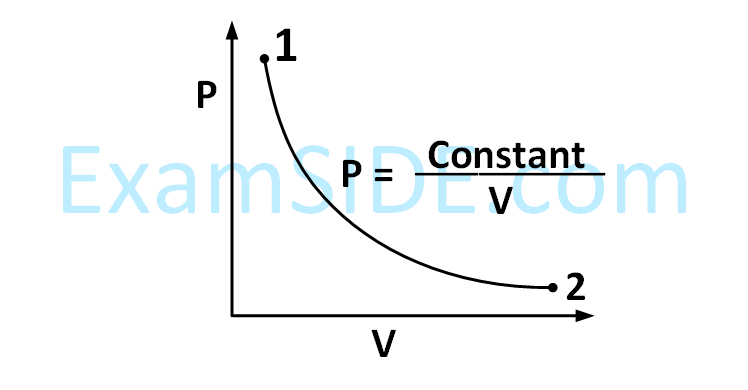
out of the following which one correctly represents the T-P diagram ?

out of the following which one correctly represents the T-P diagram ?
24
A uniform magnetic field B of 0.3 T is along the positive Z-direction. A rectangular loop (abcd) of sides 10 cm × 5 cm carries a current I of 12 A. Out of the following different orientations which one
corresponds to stable equilibrium ?
25
In a meter bridge experiment resistances are connected as shown in the figure. Initially resistance P = 4 $$\Omega $$ and the neutral point N is at 60 cm from A. Now an unknown resistance R is connected in series to P and the new position of the neutral point is at 80 cm from A. The value of unknown resistance R is :


26
A combination of parallel plate capacitors is maintained at a certain potential difference.

When a 3 mm thick slab is introduced between all the plates, in order to maintain the same potential difference, the distance between the plates is increased by 2.4 mm. Find the dielectric constant of the slab.

When a 3 mm thick slab is introduced between all the plates, in order to maintain the same potential difference, the distance between the plates is increased by 2.4 mm. Find the dielectric constant of the slab.
27
Four closed surfaces and corresponding charge distributions are shown below.

Let the respective electric fluxes through the surfaces be $${\Phi _1},$$ $${\Phi _2},$$ $${\Phi _3}$$ and $${\Phi _4}$$. Then :

Let the respective electric fluxes through the surfaces be $${\Phi _1},$$ $${\Phi _2},$$ $${\Phi _3}$$ and $${\Phi _4}$$. Then :