JEE Main 2020 (Online) 2nd September Evening Slot
Paper was held on
Wed, Sep 2, 2020 9:30 AM
Chemistry
1
For the disproportionation reaction
2Cu+(aq) ⇌ Cu(s) + Cu2+(aq) at 298 K. ln K
(where K is the equilibrium constant) is
___________ × 10–1.
Given :
($$E_{C{u^{2 + }}/C{u^ + }}^0 = 0.16V$$
$$E_{C{u^ + }/Cu}^0 = 0.52V$$
$${{RT} \over F} = 0.025$$)
2Cu+(aq) ⇌ Cu(s) + Cu2+(aq) at 298 K. ln K
(where K is the equilibrium constant) is
___________ × 10–1.
Given :
($$E_{C{u^{2 + }}/C{u^ + }}^0 = 0.16V$$
$$E_{C{u^ + }/Cu}^0 = 0.52V$$
$${{RT} \over F} = 0.025$$)
2
The ratio of the mass percentages of ‘C & H’
and ‘C & O’ of a saturated acyclic organic
compound ‘X’ are 4 : 1 and 3 : 4 respectively.
Then, the moles of oxygen gas required for
complete combustion of two moles of organic
compound ‘X’ is ________.
3
The work function of sodium metal is
4.41 $$ \times $$ 10–19 J. If photons of wavelength 300 nm
are incident on the metal, the kinetic energy of
the ejected electrons will be (h = 6.63 $$ \times $$ 10–34 J s;
c = 3 $$ \times $$ 108 m/s) ________ × 10–21 J.
4
The oxidation states of transition metal atoms
in K2Cr2O7, KMnO4 and K2FeO4, respectively,
are x, y and z. The sum of x, y and z is _______.
5
The heat of combustion of ethanol into carbon
dioxide and water is – 327 kcal at constant
pressure. The heat evolved (in cal) at constant
volume and 27oC (if all gases behave ideally) is
(R = 2 cal mol–1 K–1) ________.
6
The correct observation in the following
reactions is :
7
The major product of the following reaction is :
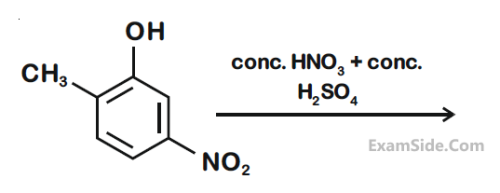

8
The shape / structure of [XeF5]– and XeO3F2,
respectively, are
9
An organic compound ‘A’ (C9H10O) when
treated with conc. HI undergoes cleavage to
yield compounds ‘B’ and ‘C’. ‘B’ gives yellow
precipitate with AgNO3 where as ‘C’
tautomerizes to ‘D’. ‘D’ gives positive iodoform
test. ‘A’ could be
10
The molecular geometry of SF6 is octahedral.
What is the geometry of SF4 (including lone
pair(s) of electrons, if any)?
11
Two compounds A and B with same molecular
formula (C3H6O) undergo Grignard’s reaction
with methylmagnesium bromide to give
products C and D. Products C and D show
following chemical tests.

C and D respectively are :

C and D respectively are :
12
Match the type of interaction in column A with
the distance dependence of their interaction
energy in column B
| A | B |
|---|---|
| (i) ion-ion | (a) $${1 \over r}$$ |
| (ii) dipole-dipole | (b) $${1 \over {{r^2}}}$$ |
| (iii) London dispersion | (c) $${1 \over {{r^3}}}$$ |
| (d) $${1 \over {{r^6}}}$$ |
13
The results given in the below table were
obtained during kinetic studies of the following
reaction
2A + B $$ \to $$ C + D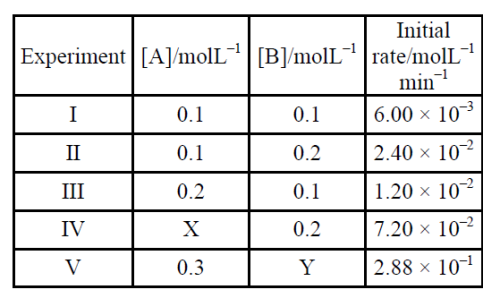
X and Y in the given table are respectively :
2A + B $$ \to $$ C + D

X and Y in the given table are respectively :
14
The size of a raw mango shrinks to a much
smaller size when kept in a concentrated salt
solution. Which one of the following processes
can explain this?
15
The one that is not expected to show isomerism
is :
16
Simplified absorption spectra of three
complexes ((i), (ii) and (iii)) of Mn+ ion are
provided below; their $$\lambda $$max values are marked
as A, B and C respectively. The correct match
between the complexes and their $$\lambda $$max values is
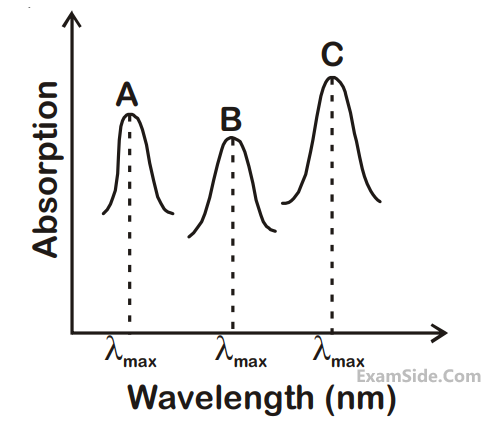
(i) [M(NCS)6](–6 + n)
(ii) [MF6](–6 + n)
(iii) [M(NH3)6]n+

(i) [M(NCS)6](–6 + n)
(ii) [MF6](–6 + n)
(iii) [M(NH3)6]n+
17
If you spill a chemical toilet cleaning liquid on
your hand, your first aid would be
18
The number of subshells associated with n = 4
and m = –2 quantum numbers is
19
The major product obtained from
E2 - elimination of 3-bromo-2-fluoropentane is
20
Three elements X, Y and Z are in the 3rd period
of the periodic table. The oxides of X, Y and Z,
respectively, are basic, amphoteric and acidic.
The correct order of the atomic numbers of X,
Y and Z is :
21
Consider the reaction sequence given below:
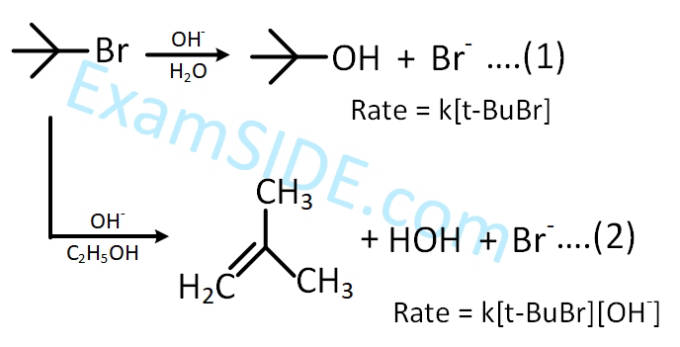
Which of the following statements is true?

Which of the following statements is true?
22
Arrange the following labelled hydrogens in
decreasing order of acidity :
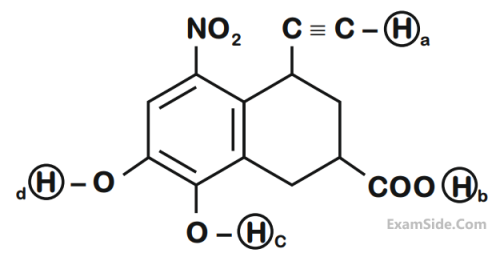

Mathematics
1
Let a, b, c $$ \in $$ R be all non-zero and satisfy
a3 + b3 + c3 = 2. If the matrix
A = $$\left( {\matrix{ a & b & c \cr b & c & a \cr c & a & b \cr } } \right)$$
satisfies ATA = I, then a value of abc can be :
a3 + b3 + c3 = 2. If the matrix
A = $$\left( {\matrix{ a & b & c \cr b & c & a \cr c & a & b \cr } } \right)$$
satisfies ATA = I, then a value of abc can be :
2
Let f : R $$ \to $$ R be a function which satisfies
f(x + y) = f(x) + f(y) $$\forall $$ x, y $$ \in $$ R. If f(1) = 2 and
g(n) = $$\sum\limits_{k = 1}^{\left( {n - 1} \right)} {f\left( k \right)} $$, n $$ \in $$ N then the value of n, for which g(n) = 20, is :
f(x + y) = f(x) + f(y) $$\forall $$ x, y $$ \in $$ R. If f(1) = 2 and
g(n) = $$\sum\limits_{k = 1}^{\left( {n - 1} \right)} {f\left( k \right)} $$, n $$ \in $$ N then the value of n, for which g(n) = 20, is :
3
If the equation cos4 $$\theta $$ + sin4 $$\theta $$ +
$$\lambda $$ = 0 has real
solutions for
$$\theta $$, then
$$\lambda $$ lies in the interval :
4
Let f(x) be a quadratic polynomial such that
f(–1) + f(2) = 0. If one of the roots of f(x) = 0
is 3, then its other root lies in :
f(–1) + f(2) = 0. If one of the roots of f(x) = 0
is 3, then its other root lies in :
5
Let n > 2 be an integer. Suppose that there are
n Metro stations in a city located along a
circular path. Each pair of stations is connected
by a straight track only. Further, each pair of
nearest stations is connected by blue line,
whereas all remaining pairs of stations are
connected by red line. If the number of red lines
is 99 times the number of blue lines, then the
value of n is :
6
The area (in sq. units) of an equilateral triangle
inscribed in the parabola y2 = 8x, with one of
its vertices on the vertex of this parabola, is :
7
If the sum of first 11 terms of an A.P.,
a1, a2, a3, .... is 0 (a $$ \ne $$ 0), then the sum of the A.P.,
a1 , a3 , a5 ,....., a23 is ka1 , where k is equal to :
a1, a2, a3, .... is 0 (a $$ \ne $$ 0), then the sum of the A.P.,
a1 , a3 , a5 ,....., a23 is ka1 , where k is equal to :
8
If a curve y = f(x), passing through the point
(1, 2), is the solution of the differential equation,
2x2dy= (2xy + y2)dx, then $$f\left( {{1 \over 2}} \right)$$ is equal to :
2x2dy= (2xy + y2)dx, then $$f\left( {{1 \over 2}} \right)$$ is equal to :
9
Let the position vectors of points 'A' and 'B' be
$$\widehat i + \widehat j + \widehat k$$ and $$2\widehat i + \widehat j + 3\widehat k$$, respectively. A point 'P' divides the line segment AB internally in the ratio $$\lambda $$ : 1 ( $$\lambda $$ > 0). If O is the origin and
$$\overrightarrow {OB} .\overrightarrow {OP} - 3{\left| {\overrightarrow {OA} \times \overrightarrow {OP} } \right|^2} = 6$$, then $$\lambda $$ is equal to______.
$$\widehat i + \widehat j + \widehat k$$ and $$2\widehat i + \widehat j + 3\widehat k$$, respectively. A point 'P' divides the line segment AB internally in the ratio $$\lambda $$ : 1 ( $$\lambda $$ > 0). If O is the origin and
$$\overrightarrow {OB} .\overrightarrow {OP} - 3{\left| {\overrightarrow {OA} \times \overrightarrow {OP} } \right|^2} = 6$$, then $$\lambda $$ is equal to______.
10
Let [t] denote the greatest integer less than or
equal to t.
Then the value of $$\int\limits_1^2 {\left| {2x - \left[ {3x} \right]} \right|dx} $$ is ______.
Then the value of $$\int\limits_1^2 {\left| {2x - \left[ {3x} \right]} \right|dx} $$ is ______.
11
If y = $$\sum\limits_{k = 1}^6 {k{{\cos }^{ - 1}}\left\{ {{3 \over 5}\cos kx - {4 \over 5}\sin kx} \right\}} $$,
then $${{dy} \over {dx}}$$ at x = 0 is _______.
then $${{dy} \over {dx}}$$ at x = 0 is _______.
12
The set of all possible values of
$$\theta $$ in the interval
(0, $$\pi $$) for which the points (1, 2) and (sin $$\theta $$, cos $$\theta $$) lie
on the same side of the line x + y = 1 is :
(0, $$\pi $$) for which the points (1, 2) and (sin $$\theta $$, cos $$\theta $$) lie
on the same side of the line x + y = 1 is :
13
If the variance of the terms in an increasing A.P.,
b1 , b2 , b3 ,....,b11 is 90, then the common difference of this A.P. is_______.
b1 , b2 , b3 ,....,b11 is 90, then the common difference of this A.P. is_______.
14
Let A = {X = (x, y, z)T: PX = 0 and
x2 + y2 + z2 = 1} where
$$P = \left[ {\matrix{ 1 & 2 & 1 \cr { - 2} & 3 & { - 4} \cr 1 & 9 & { - 1} \cr } } \right]$$,
then the set A :
x2 + y2 + z2 = 1} where
$$P = \left[ {\matrix{ 1 & 2 & 1 \cr { - 2} & 3 & { - 4} \cr 1 & 9 & { - 1} \cr } } \right]$$,
then the set A :
15
Consider a region R = {(x, y) $$ \in $$ R : x2 $$ \le $$ y $$ \le $$ 2x}.
if a line y = $$\alpha $$ divides the area of region R into
two equal parts, then which of the following is
true?
16
Let EC denote the complement of an event E.
Let E1
, E2
and E3
be any pairwise independent
events with P(E1) > 0
and P(E1 $$ \cap $$ E2 $$ \cap $$ E3) = 0.
Then P($$E_2^C \cap E_3^C/{E_1}$$) is equal to :
and P(E1 $$ \cap $$ E2 $$ \cap $$ E3) = 0.
Then P($$E_2^C \cap E_3^C/{E_1}$$) is equal to :
17
For some $$\theta \in \left( {0,{\pi \over 2}} \right)$$, if the eccentricity of the
hyperbola, x2–y2sec2$$\theta $$ = 10 is $$\sqrt 5 $$ times the
eccentricity of the ellipse, x2sec2$$\theta $$ + y2 = 5, then the length of the latus rectum of the ellipse, is :
hyperbola, x2–y2sec2$$\theta $$ = 10 is $$\sqrt 5 $$ times the
eccentricity of the ellipse, x2sec2$$\theta $$ + y2 = 5, then the length of the latus rectum of the ellipse, is :
18
$$\mathop {\lim }\limits_{x \to 0} {\left( {\tan \left( {{\pi \over 4} + x} \right)} \right)^{{1 \over x}}}$$ is equal to :
19
The imaginary part of
$${\left( {3 + 2\sqrt { - 54} } \right)^{{1 \over 2}}} - {\left( {3 - 2\sqrt { - 54} } \right)^{{1 \over 2}}}$$ can be :
$${\left( {3 + 2\sqrt { - 54} } \right)^{{1 \over 2}}} - {\left( {3 - 2\sqrt { - 54} } \right)^{{1 \over 2}}}$$ can be :
20
Let f : (–1,
$$\infty $$)
$$ \to $$ R be defined by f(0) = 1 and
f(x) = $${1 \over x}{\log _e}\left( {1 + x} \right)$$, x $$ \ne $$ 0. Then the function f :
f(x) = $${1 \over x}{\log _e}\left( {1 + x} \right)$$, x $$ \ne $$ 0. Then the function f :
Physics
1
An inductance coil has a reactance of 100 $$\Omega $$.
When an AC signal of frequency 1000 Hz is
applied to the coil, the applied voltage leads
the current by 45o. The self-inductance of the
coil is
2
In the following digital circuit, what will be the
output at ‘Z’, when the
input (A, B) are (1, 0), (0, 0), (1, 1,), (0, 1)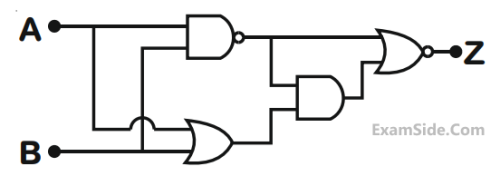
input (A, B) are (1, 0), (0, 0), (1, 1,), (0, 1)

3
A charge Q is distributed over two concentric
conducting thin spherical shells radii r and
R (R > r). If the surface charge densities on the
two shells are equal, the electric potential at
the common centre is :
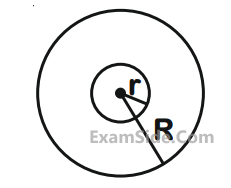

4
Two uniform circular discs are rotating
independently in the same direction around
their common axis passing through their
centres. The moment of inertia and angular
velocity of the first disc are 0.1 kg-m2 and 10
rad s–1 respectively while those for the second
one are 0.2 kg-m2 and 5 rad s–1 respectively. At
some instant they get stuck together and start
rotating as a single system about their common
axis with some angular speed. The kinetic
energy of the combined system is :
5
A small point mass carrying some positive
charge on it, is released from the edge of a
table. There is a uniform electric field in this
region in the horizontal direction. Which of the
following options then correctly describe the
trajectory of the mass?
(Curves are drawn schematically and are not to scale).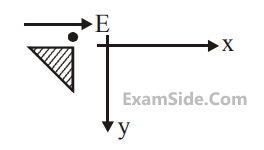
(Curves are drawn schematically and are not to scale).

6
The height ‘h’ at which the weight of a body will
be the same as that at the same depth ‘h’ from
the surface of the earth is (Radius of the earth
is R and effect of the rotation of the earth is
neglected)
7
A particle is moving 5 times as fast as an
electron. The ratio of the de-Broglie wavelength
of the particle to that of the electron is 1.878 $$ \times $$
10–4. The mass of the particle is close to
8
A 10 $$\mu $$F capacitor is fully charged to a potential
difference of 50 V. After removing the source
voltage it is connected to an uncharged
capacitor in parallel. Now the potential
difference across them becomes 20 V. The
capacitance of the second capacitor is :
9
A wire carrying current I is bent in the shape
ABCDEFA as shown, where rectangle ABCDA
and ADEFA are perpendicular to each other. If
the sides of the rectangles are of lengths a and
b, then the magnitude and direction of
magnetic moment of the loop ABCDEFA is
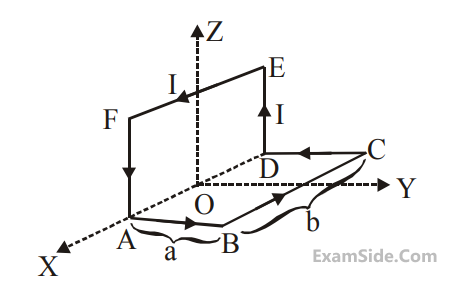

10
A capillary tube made of glass of radius 0.15
mm is dipped vertically in a beaker filled with
methylene iodide (surface tension = 0.05 Nm–1,
density = 667 kg m–3) which rises to height h in
the tube. It is observed that the two tangents
drawn from liquid-glass interfaces (from opp.
sides of the capillary) make an angle of 60o
with one another. Then h is close to (g = 10 ms–2)
11
The figure shows a region of length ‘l’ with a
uniform magnetic field of 0.3 T in it and a
proton entering the region with velocity 4 $$ \times $$ 105
ms–1 making an angle 60o with the field. If the
proton completes 10 revolution by the time it
cross the region shown, ‘l’ is close to
(mass of proton = 1.67 $$ \times $$ 10–27 kg, charge of the proton = 1.6 $$ \times $$ 10–19 C)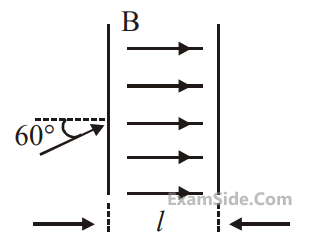
(mass of proton = 1.67 $$ \times $$ 10–27 kg, charge of the proton = 1.6 $$ \times $$ 10–19 C)

12
The displacement time graph of a particle
executing S.H.M is given in figure :
(sketch is schematic and not to scale)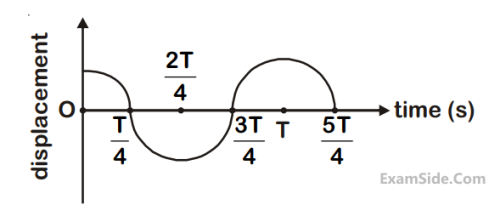
Which of the following statements is/are true for this motion?
(A) The force is zero at t = $${{3T} \over 4}$$
(B) The acceleration is maximum at t = T
(C) The speed is maximum at t = $${{T} \over 4}$$
(D) The P.E. is equal to K.E. of the oscillation at t = $${{T} \over 2}$$
(sketch is schematic and not to scale)

Which of the following statements is/are true for this motion?
(A) The force is zero at t = $${{3T} \over 4}$$
(B) The acceleration is maximum at t = T
(C) The speed is maximum at t = $${{T} \over 4}$$
(D) The P.E. is equal to K.E. of the oscillation at t = $${{T} \over 2}$$
13
If momentum (P), area (A) and time (T) are
taken to be the fundamental quantities then the
dimensional formula for energy is
14
In a hydrogen atom the electron makes a
transition from (n + 1)th level to the nth level.
If n >> 1, the frequency of radiation emitted is
proportional to :
15
An ideal gas in a closed container is slowly
heated. As its temperature increases, which of
the following statements are true?
(A) the mean free path of the molecules decreases.
(B) the mean collision time between the molecules decreases.
(C) the mean free path remains unchanged.
(D) the mean collision time remains unchanged.
(A) the mean free path of the molecules decreases.
(B) the mean collision time between the molecules decreases.
(C) the mean free path remains unchanged.
(D) the mean collision time remains unchanged.
16
When the temperature of a metal wire is
increased from 0oC to 10oC, its length
increases by 0.02%. The percentage change in
its mass density will be closest to :
17
In a Young’s double slit experiment, 16 fringes
are observed in a certain segment of the
screen when light of a wavelength 700 nm is
used. If the wavelength of light is changed to
400 nm, the number of fringes observed in the
same segment of the screen would be
18
A light ray enters a solid glass sphere of
refractive index $$\mu $$ = $$\sqrt 3 $$ at an angle of incidence
60o. The ray is both reflected and refracted at
the farther surface of the sphere. The angle (in
degrees) between the reflected and refracted
rays at this surface is ________.
19
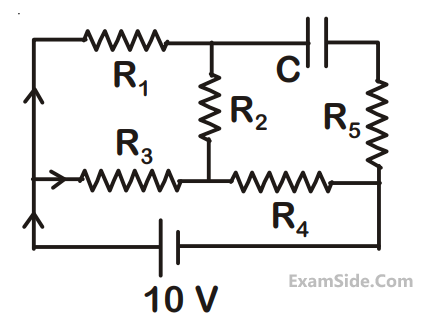
An ideal cell of emf 10 V is connected in circuit
shown in figure. Each resistance is 2 $$\Omega $$. The
potential difference (in V) across the capacitor
when it is fully charged is ______.

20
In a plane electromagnetic wave, the directions
of electric field and magnetic field are
represented by $$\widehat k$$ and $$2\widehat i - 2\widehat j$$, respectively.
What is the unit vector along direction of
propagation of the wave?
21
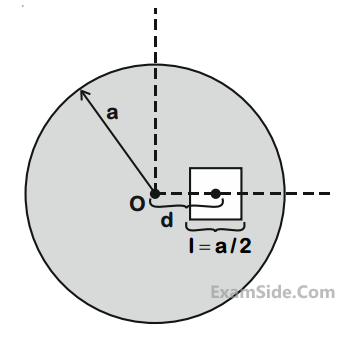
A square shaped hole of side l = $${a \over 2}$$ is carved
out at a distance d = $${a \over 2}$$ from the centre ‘O’ of
a uniform circular disk of radius a. If the
distance of the centre of mass of the
remaining portion form O is
$$ - {a \over X}$$ , value of X (to
the nearest integer) is :

22
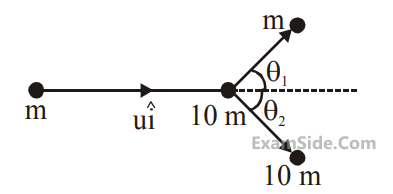
A particle of mass m is moving along the x-axis
with initial velocity $$u\widehat i$$. It collides elastically
with a particle of mass 10 m at rest and then
moves with half its initial kinetic energy (see
figure). If $$\sin {\theta _1} = \sqrt n \sin {\theta _2}$$ then value of n is
________.

23
A wire of density 9 $$ \times $$ 10–3 kg cm–3 is stretched
between two clamps 1 m apart. The resulting
strain in the wire is 4.9 $$ \times $$ 10–4. The lowest
frequency of the transverse vibrations in the
wire is : (Young’s modulus of wire Y = 9 $$ \times $$ 1010
Nm–2), (to the nearest integer), _________