JEE Main 2021 (Online) 26th February Evening Shift
Paper was held on
Fri, Feb 26, 2021 9:30 AM
Chemistry
1
Match List - I with List - II.
Choose the correct answer from the options given below :
| List - I (Molecule) | List - II (Bond order) | ||
|---|---|---|---|
| (a) | $$N{e_2}$$ | (i) | 1 |
| (b) | $${N_2}$$ | (ii) | 2 |
| (c) | $${F_2}$$ | (iii) | 0 |
| (d) | $${O_2}$$ | (iv) | 3 |
Choose the correct answer from the options given below :
2
Ceric ammonium nitrate and CHCl3/alc. KOH are used for the identification of functional groups present in __________ and _______ respectively.
3
In $$\mathop C\limits^1 {H_2} = \mathop C\limits^2 = \mathop C\limits^3 H - \mathop C\limits^4 {H_3}$$ molecule, the hybridization of carbon 1, 2, 3 and 4 respectively, are :
4
A. Phenyl methanamine
B. N,N-Dimethylaniline
C. N-Methyl aniline
D. Benzenamine
Choose the correct order of basic nature of the above amines.
B. N,N-Dimethylaniline
C. N-Methyl aniline
D. Benzenamine
Choose the correct order of basic nature of the above amines.
5
Given below are two statements : one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A : In TlI3, isomorphous to CsI3, the metal is present in +1 oxidation state.
Reason R : Tl metal has fourteen f electrons in its electronic configuration.
In the light of the above statements, choose the most appropriate answer from the options given below :
Assertion A : In TlI3, isomorphous to CsI3, the metal is present in +1 oxidation state.
Reason R : Tl metal has fourteen f electrons in its electronic configuration.
In the light of the above statements, choose the most appropriate answer from the options given below :
6
Which of the following forms of hydrogen emits low energy $$\beta$$- particles?
7
Which pair of oxides is acidic in nature?
8
Identify A in the given reaction.


9
Match List - I with List - II.

Choose the correct answer from the options given below :

Choose the correct answer from the options given below :
10
Identify A in the following chemical reaction.


11
2, 4-DNP test can be used to identify :
12

Considering the above reaction, the major product among the following is :
13
Identify A in the given chemical reaction.


14
The correct order of electron gain enthalpy is :
15
Match List - I with List - II.
Choose the correct answer from the options given below :
| List - I | List - II | ||
|---|---|---|---|
| (a) | Sucrose | (i) | $$\beta $$-D-Galactose and $$\beta $$-D-Glucose |
| (b) | Lactose | (ii) | $$\alpha $$-D-Glucose and $$\beta $$-D-Fructose |
| (c) | Maltose | (iii) | $$\alpha $$-D-Glucose and $$\alpha $$-D-Glucose |
Choose the correct answer from the options given below :
16
Seliwanoff test and Xanthoproteic test are used for the identification of ___________ and ________ respectively.
17
When 12.2 g of benzoic acid is dissolved in 100 g of water, the freezing point of solution was found to be $$-$$0.93$$^\circ$$C (Kf(H2O) = 1.86 K kg mol$$-$$1). The number (n) of benzoic acid molecules associated (assuming 100% association) is ___________.
18
If the activation energy of a reaction is 80.9 kJ mol$$-$$1, the fraction of molecules at 700 K, having enough energy to react to form
products is e$$-$$x. The value of x is __________. (Rounded off to the nearest integer) [Use R = 8.31 J K$$-$$1 mol$$-$$1]
products is e$$-$$x. The value of x is __________. (Rounded off to the nearest integer) [Use R = 8.31 J K$$-$$1 mol$$-$$1]
19
In mildly alkaline medium, thiosulphate ion is oxidized by $$MnO_4^ - $$ to "A". The oxidation state of sulphur in "A" is __________.
20
The average S-F bond energy in kJ mol$$-$$1 of SF6 is _____________. (Rounded off to the nearest integer)
[Given : The values of standard enthalpy of formation of SF6(g), S(g) and F(g) are - 1100, 275 and 80 kJ mol$$-$$1 respectively.]
[Given : The values of standard enthalpy of formation of SF6(g), S(g) and F(g) are - 1100, 275 and 80 kJ mol$$-$$1 respectively.]
21
Emf of the following cell at 298K in V is x $$\times$$ 10$$-$$2.
Zn|Zn2+(0.1 M)||Ag+ (0.01 M)|Ag
The value of x is _________. (Rounded off to the nearest integer)
[Given : $$E_{Z{n^{2 + }}/Zn}^\theta = - 0.76V;E_{A{g^{2 + }}/Ag}^\theta = + 0.80V;{{2.303RT} \over F} = 0.059$$]
Zn|Zn2+(0.1 M)||Ag+ (0.01 M)|Ag
The value of x is _________. (Rounded off to the nearest integer)
[Given : $$E_{Z{n^{2 + }}/Zn}^\theta = - 0.76V;E_{A{g^{2 + }}/Ag}^\theta = + 0.80V;{{2.303RT} \over F} = 0.059$$]
22
The pH of ammonium phosphate solution, if pka of phosphoric acid and pkb of ammonium hydroxide are 5.23 and 4.75 respectively, is ___________.
23
The number of stereoisomers possible for [Co(ox)2(Br)(NH3)]2$$-$$ is ___________. [ox = oxalate]
24
A ball weighing 10 g is moving with a velocity of 90 ms$$-$$1. If the uncertainty in its velocity is 5%, then the uncertainty in its position is ___________ $$\times$$ 10$$-$$33 m. (Rounded off to the nearest integer)
[Given : h = 6.63 $$\times$$ 10$$-$$34 Js]
[Given : h = 6.63 $$\times$$ 10$$-$$34 Js]
25
The NaNO3 weighed out to make 50 mL of an aqueous solution containing 70.0 mg Na+ per mL is _________ g. (Rounded off to the nearest integer)
[Given : Atomic weight in g mol$$-$$1 - Na : 23; N : 14; O : 16]
[Given : Atomic weight in g mol$$-$$1 - Na : 23; N : 14; O : 16]
Mathematics
1
Let f(x) be a differentiable function at x = a with f'(a) = 2 and f(a) = 4.
Then $$\mathop {\lim }\limits_{x \to a} {{xf(a) - af(x)} \over {x - a}}$$ equals :
Then $$\mathop {\lim }\limits_{x \to a} {{xf(a) - af(x)} \over {x - a}}$$ equals :
2
Let A(1, 4) and B(1, $$-$$5) be two points. Let P be a point on the circle
(x $$-$$ 1)2 + (y $$-$$ 1)2 = 1 such that (PA)2 + (PB)2 have maximum value, then the points, P, A and B lie on :
(x $$-$$ 1)2 + (y $$-$$ 1)2 = 1 such that (PA)2 + (PB)2 have maximum value, then the points, P, A and B lie on :
3
Consider the following system of equations :
x + 2y $$-$$ 3z = a
2x + 6y $$-$$ 11z = b
x $$-$$ 2y + 7z = c,
where a, b and c are real constants. Then the system of equations :
x + 2y $$-$$ 3z = a
2x + 6y $$-$$ 11z = b
x $$-$$ 2y + 7z = c,
where a, b and c are real constants. Then the system of equations :
4
A natural number has prime factorization given by n = 2x3y5z, where y and z are such
that y + z = 5 and y$$-$$1 + z$$-$$1 = $${5 \over 6}$$, y > z. Then the number of odd divisions of n, including 1, is :
that y + z = 5 and y$$-$$1 + z$$-$$1 = $${5 \over 6}$$, y > z. Then the number of odd divisions of n, including 1, is :
5
If 0 < a, b < 1, and tan$$-$$1a + tan$$-$$1b = $${\pi \over 4}$$, then the value of
$$(a + b) - \left( {{{{a^2} + {b^2}} \over 2}} \right) + \left( {{{{a^3} + {b^3}} \over 3}} \right) - \left( {{{{a^4} + {b^4}} \over 4}} \right) + .....$$ is :
$$(a + b) - \left( {{{{a^2} + {b^2}} \over 2}} \right) + \left( {{{{a^3} + {b^3}} \over 3}} \right) - \left( {{{{a^4} + {b^4}} \over 4}} \right) + .....$$ is :
6
Let $$f(x) = \int\limits_0^x {{e^t}f(t)dt + {e^x}} $$ be a differentiable function for all x$$\in$$R. Then f(x) equals :
7
For x > 0, if $$f(x) = \int\limits_1^x {{{{{\log }_e}t} \over {(1 + t)}}dt} $$, then $$f(e) + f\left( {{1 \over e}} \right)$$ is equal to :
8
Let $$A = \{ 1,2,3,....,10\} $$ and $$f:A \to A$$ be defined as
$$f(k) = \left\{ {\matrix{ {k + 1} & {if\,k\,is\,odd} \cr k & {if\,k\,is\,even} \cr } } \right.$$
Then the number of possible functions $$g:A \to A$$ such that $$gof = f$$ is :
$$f(k) = \left\{ {\matrix{ {k + 1} & {if\,k\,is\,odd} \cr k & {if\,k\,is\,even} \cr } } \right.$$
Then the number of possible functions $$g:A \to A$$ such that $$gof = f$$ is :
9
Let A1 be the area of the region bounded by the curves y = sinx, y = cosx and y-axis in the first quadrant. Also, let A2 be the area of the region bounded by the curves y = sinx, y = cosx, x-axis and x = $${\pi \over 2}$$ in the first quadrant. Then,
10
Let $$f(x) = {\sin ^{ - 1}}x$$ and $$g(x) = {{{x^2} - x - 2} \over {2{x^2} - x - 6}}$$. If $$g(2) = \mathop {\lim }\limits_{x \to 2} g(x)$$, then the domain of the function fog is :
11
Let f : R $$ \to $$ R be defined as
$$f(x) = \left\{ \matrix{ 2\sin \left( { - {{\pi x} \over 2}} \right),if\,x < - 1 \hfill \cr |a{x^2} + x + b|,\,if - 1 \le x \le 1 \hfill \cr \sin (\pi x),\,if\,x > 1 \hfill \cr} \right.$$ If f(x) is continuous on R, then a + b equals :
$$f(x) = \left\{ \matrix{ 2\sin \left( { - {{\pi x} \over 2}} \right),if\,x < - 1 \hfill \cr |a{x^2} + x + b|,\,if - 1 \le x \le 1 \hfill \cr \sin (\pi x),\,if\,x > 1 \hfill \cr} \right.$$ If f(x) is continuous on R, then a + b equals :
12
If the locus of the mid-point of the line segment from the point (3, 2) to a point on the circle, x2 + y2 = 1 is a circle of radius r, then r is equal to :
13
If vectors $$\overrightarrow {{a_1}} = x\widehat i - \widehat j + \widehat k$$ and $$\overrightarrow {{a_2}} = \widehat i + y\widehat j + z\widehat k$$ are collinear, then a possible unit vector parallel to the vector $$x\widehat i + y\widehat j + z\widehat k$$ is :
14
A seven digit number is formed using digits 3, 3, 4, 4, 4, 5, 5. The probability, that number so formed is divisible by 2, is :
15
The total number of 4-digit numbers whose greatest common divisor with 18 is 3, is _________.
16
If the matrix $$A = \left[ {\matrix{
1 & 0 & 0 \cr
0 & 2 & 0 \cr
3 & 0 & { - 1} \cr
} } \right]$$ satisfies the equation
$${A^{20}} + \alpha {A^{19}} + \beta A = \left[ {\matrix{ 1 & 0 & 0 \cr 0 & 4 & 0 \cr 0 & 0 & 1 \cr } } \right]$$ for some real numbers $$\alpha$$ and $$\beta$$, then $$\beta$$ $$-$$ $$\alpha$$ is equal to ___________.
$${A^{20}} + \alpha {A^{19}} + \beta A = \left[ {\matrix{ 1 & 0 & 0 \cr 0 & 4 & 0 \cr 0 & 0 & 1 \cr } } \right]$$ for some real numbers $$\alpha$$ and $$\beta$$, then $$\beta$$ $$-$$ $$\alpha$$ is equal to ___________.
17
Let $$\alpha$$ and $$\beta$$ be two real numbers such that $$\alpha$$ + $$\beta$$ = 1 and $$\alpha$$$$\beta$$ = $$-$$1. Let pn = ($$\alpha$$)n + ($$\beta$$)n, pn$$-$$1 = 11 and pn+1 = 29 for some integer n $$ \ge $$ 1. Then, the value of p$$_n^2$$ is ___________.
18
Let z be those complex numbers which satisfy
| z + 5 | $$ \le $$ 4 and z(1 + i) + $$\overline z $$(1 $$-$$ i) $$ \ge $$ $$-$$10, i = $$\sqrt { - 1} $$.
If the maximum value of | z + 1 |2 is $$\alpha$$ + $$\beta$$$$\sqrt 2 $$, then the value of ($$\alpha$$ + $$\beta$$) is ____________.
| z + 5 | $$ \le $$ 4 and z(1 + i) + $$\overline z $$(1 $$-$$ i) $$ \ge $$ $$-$$10, i = $$\sqrt { - 1} $$.
If the maximum value of | z + 1 |2 is $$\alpha$$ + $$\beta$$$$\sqrt 2 $$, then the value of ($$\alpha$$ + $$\beta$$) is ____________.
19
If the arithmetic mean and geometric mean of the pth and qth terms of the
sequence $$-$$16, 8, $$-$$4, 2, ...... satisfy the equation
4x2 $$-$$ 9x + 5 = 0, then p + q is equal to __________.
sequence $$-$$16, 8, $$-$$4, 2, ...... satisfy the equation
4x2 $$-$$ 9x + 5 = 0, then p + q is equal to __________.
20
If $${I_{m,n}} = \int\limits_0^1 {{x^{m - 1}}{{(1 - x)}^{n - 1}}dx} $$, for m, $$n \ge 1$$, and
$$\int\limits_0^1 {{{{x^{m - 1}} + {x^{n - 1}}} \over {{{(1 + x)}^{m + 1}}}}} dx = \alpha {I_{m,n}}\alpha \in R$$, then $$\alpha$$ equals ___________.
$$\int\limits_0^1 {{{{x^{m - 1}} + {x^{n - 1}}} \over {{{(1 + x)}^{m + 1}}}}} dx = \alpha {I_{m,n}}\alpha \in R$$, then $$\alpha$$ equals ___________.
21
Let X1, X2, ......., X18 be eighteen observations such
that $$\sum\limits_{i = 1}^{18} {({X_i} - } \alpha ) = 36$$ and $$\sum\limits_{i = 1}^{18} {({X_i} - } \beta {)^2} = 90$$, where $$\alpha$$ and $$\beta$$ are distinct real numbers. If the standard deviation of these observations is 1, then the value of | $$\alpha$$ $$-$$ $$\beta$$ | is ____________.
that $$\sum\limits_{i = 1}^{18} {({X_i} - } \alpha ) = 36$$ and $$\sum\limits_{i = 1}^{18} {({X_i} - } \beta {)^2} = 90$$, where $$\alpha$$ and $$\beta$$ are distinct real numbers. If the standard deviation of these observations is 1, then the value of | $$\alpha$$ $$-$$ $$\beta$$ | is ____________.
22
Let a be an integer such that all the real roots of the polynomial
2x5 + 5x4 + 10x3 + 10x2 + 10x + 10 lie in the interval (a, a + 1). Then, |a| is equal to ___________.
2x5 + 5x4 + 10x3 + 10x2 + 10x + 10 lie in the interval (a, a + 1). Then, |a| is equal to ___________.
Physics
1
Draw the output signal Y in the given combination of gates.


2
An aeroplane, with its wings spread 10 m, is flying at a speed of 180 km/h in a horizontal direction. The total intensity of earth's field at that part is 2.5 $$\times$$ 10$$-$$4 Wb/m2 and the angle of dip is 60$$^\circ$$. The emf induced between the tips of the plane wings will be __________.
3
Find the peak current and resonant frequency of the following circuit (as shown in figure).
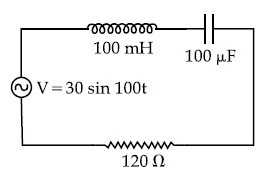

4
A scooter accelerates from rest for time t1 at constant rate a1 and then retards at constant rate a2 for time t2 and comes to rest. The correct value of $${{{t_1}} \over {{t_2}}}$$ wil be :
5
Given below are two statements:
Statement I : An electric dipole is placed at the center of a hollow sphere. The flux of the electric field through the sphere is zero but the electric field is not zero anywhere in the sphere.
Statement II : If R is the radius of a solid metallic sphere and Q be the total charge on it. The electric field at any point on the spherical surface of radius r (< R) is zero but the electric flux passing through this closed spherical surface of radius r is not zero..
In the light of the above statements, choose the correct answer from the options given below :
Statement I : An electric dipole is placed at the center of a hollow sphere. The flux of the electric field through the sphere is zero but the electric field is not zero anywhere in the sphere.
Statement II : If R is the radius of a solid metallic sphere and Q be the total charge on it. The electric field at any point on the spherical surface of radius r (< R) is zero but the electric flux passing through this closed spherical surface of radius r is not zero..
In the light of the above statements, choose the correct answer from the options given below :
6
If 'C' and 'V' represent capacity and voltage respectively then what are the dimensions of $$\lambda$$ where C/V = $$\lambda$$ ?
7
The recoil speed of a hydrogen atom after it emits a photon in going from n = 5 state to n = 1 state will be :
8
A wire of 1$$\Omega$$ has a length of 1 m. It is stretched till its length increases by 25%. The percentage change in resistance to the nearest integer is :
9
The incident ray, reflected ray and the outward drawn normal are denoted by the unit vectors $$\overrightarrow a $$, $$\overrightarrow b $$ and $$\overrightarrow c $$ respectively. Then choose the correct relation for these vectors.
10
The internal energy (U), pressure (P) and volume (V) of an ideal gas are related as U $$=$$ 3PV + 4. The gas is :
11
The length of metallic wire is l1 when tension in it is T1. It is l2 when the tension is T2. The original length of the wire will be :
12
The trajectory of a projectile in a vertical plane is y = $$\alpha$$x $$-$$ $$\beta$$x2, where $$\alpha$$ and $$\beta$$ are constants and x & y are respectively the horizontal and vertical distances of the projectile from the point of projection. The angle of projection $$\theta$$ and the maximum height attained H are respectively given by :
13
Given below are two statements : one is labeled as Assertion A and the other is labeled as Reason R.
Assertion A : For a simple microscope, the angular size of the object equals the angular size of the image.
Reason R : Magnification is achieved as the small object can be kept much closer to the eye than 25 cm and hence it subtends a large angle.
In the light of the above statements, choose the most appropriate answer from the options given below :
Assertion A : For a simple microscope, the angular size of the object equals the angular size of the image.
Reason R : Magnification is achieved as the small object can be kept much closer to the eye than 25 cm and hence it subtends a large angle.
In the light of the above statements, choose the most appropriate answer from the options given below :
14
An inclined plane making an angle of 30$$^\circ$$ with the horizontal is placed in a uniform horizontal electric field $$200{N \over C}$$ as shown in the figure. A body of mass 1 kg and charge 5 mC is allowed to slide down from rest at a height of 1 m. If the coefficient of friction is 0.2, find the time taken by the body to reach the bottom.
[g = 9.8 m/s2; $$\sin 30^\circ = {1 \over 2}$$; $$\cos 30^\circ = {{\sqrt 3 } \over 2}$$]

[g = 9.8 m/s2; $$\sin 30^\circ = {1 \over 2}$$; $$\cos 30^\circ = {{\sqrt 3 } \over 2}$$]

15
Two masses A and B, each of mass M are fixed together by a massless spring. A force acts on the mass B as shown in the figure. If the mass A starts moving away from mass B with acceleration 'a', then the acceleration of mass B will be :
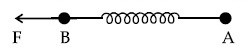
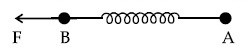
16
A cord is wound round the circumference of wheel of radius r. The axis of the wheel is horizontal and the moment of inertia about it is I. A weight mg is attached to the cord at the end. The weight falls from rest. After falling through a distance 'h', the square of angular velocity of wheel will be :
17
A particle executes S.H.M., the graph of velocity as a function of displacement is :
18
A tuning fork A of unknown frequency produces 5 beats/s with a fork of known frequency 340 Hz. When fork A is filed, the beat frequency decreases to 2 beats/s. What is the frequency of fork A?
19
Given below are two statements :
Statement I : A second's pendulum has a time period of 1 second.
Statement II : It takes precisely one second to move between the two extreme positions.
In the light of the above statements, choose the correct answer from the options given below :
Statement I : A second's pendulum has a time period of 1 second.
Statement II : It takes precisely one second to move between the two extreme positions.
In the light of the above statements, choose the correct answer from the options given below :
20
1 mole of rigid diatomic gas performs a work of $${Q \over 5}$$ when heat Q is supplied to it. The molar heat capacity of the gas during this transformation is $${xR \over 8}$$. The value of x is _________. [R = universal gas constant]
21
A particle executes S.H.M. with amplitude 'a', and time period 'T'. The displacement of the particle when its speed is half of maximum speed is $${{\sqrt x a} \over 2}$$. The value of x is __________.
22
Time period of a simple pendulum is T. The time taken to complete $${5 \over 8}$$ oscillations starting from mean position is $${\alpha \over \beta }T$$. The value of $$\alpha$$ is _________.
23
The zener diode has a Vz = 30V. The current passing through the diode for the following circuit is ________ mA.


24
The volume V of a given mass of monoatomic gas changes with temperature T according to the relation $$V = K{T^{{2 \over 3}}}$$. The workdone when temperature changes by 90K will be xR. The value of x is _________. [R = universal gas constant]
25
27 similar drops of mercury are maintained at 10V each. All these spherical drops combine into a single big drop. The potential energy of the bigger drop is __________ times that of a smaller drop.
26
A point source of light S, placed at a distance 60cm in front of the centre of a plane mirror of width 50 cm, hangs vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror at a distance 1.2 m from it (see in the figure). The distance between the extreme points where he can see the image of the light source in the mirror is __________ cm.


27
In the reported figure of earth, the value of acceleration due to gravity is same at point A and C but it is smaller than that of its value at point B (surface of the earth). The value of OA : AB will be x : y. The value of x is ________.


28
Two stream of photons, possessing energies equal to twice and ten times the work function of metal are incident on the metal surface successively. The value of ratio of maximum velocities of the photoelectrons emitted in the two respective cases is x : y. The value of x is ___________.