AIEEE 2007
Paper was held on
Sun, Apr 29, 2007 9:30 AM
Chemistry
1
The compound formed as a result of oxidation of ethyl benzene by KMnO4 is :
2
Which one of the following conformation of cyclohexane is chiral?
3
Presence of a nitro group in a benzene ring
4
The pKa of a weak acid (HA) is 4.5. The pOH of an aqueous buffered solution of HA in which 50% of
the acid is ionized is :
5
In a sautrated solution of the sparingly soluble strong electrolyte AgIO3 (Molecular mass = 283) the
equilibrium which sets in is
AgIO3(s) $$\leftrightharpoons$$ Ag+(aq) + $$IO_3^-$$
If the solubility product constant Ksp of AgIO3 at a given temperature is 1.0 $$\times$$10−8, what is the mass of AgIO3 contained in 100 ml of its saturated solution?
AgIO3(s) $$\leftrightharpoons$$ Ag+(aq) + $$IO_3^-$$
If the solubility product constant Ksp of AgIO3 at a given temperature is 1.0 $$\times$$10−8, what is the mass of AgIO3 contained in 100 ml of its saturated solution?
6
The first and second dissociation constants of an acid H2A are 1.0 $$\times$$ 10−5
and 5.0 $$\times$$ 10−10 respectively. The overall dissociation constant of the acid will be :
7
Identify the correct statement regarding a spontaneous process :
8
In conversion of lime-stone to lime,
CaCO3(s) $$\to$$ CaO(s) + CO2 (g) the vales of ∆H° and ∆S° are +179.1 kJ mol−1 and 160.2 J/K respectively at 298 K and 1 bar. Assuming that ∆H° do not change with temperature, temperature above which conversion of limestone to lime will be spontaneous is :
CaCO3(s) $$\to$$ CaO(s) + CO2 (g) the vales of ∆H° and ∆S° are +179.1 kJ mol−1 and 160.2 J/K respectively at 298 K and 1 bar. Assuming that ∆H° do not change with temperature, temperature above which conversion of limestone to lime will be spontaneous is :
9
Which of the following reactions will yield 2, 2-dibromopropane?
10
The actinoids exhibits more number of oxidation states in general than the lanthanoids. This is
because :
11
The stability of dihalides of $$Si,Ge,Sn$$ and $$Pb$$ increases steadily in the sequence :
12
Which of the following molecules is expected to rotate the plane of plane - polarized light?
13

14
Assuming that water vapour is an ideal gas, the internal energy change $$\left( {\Delta U} \right)$$ when $$1$$ mol of water is vapourised at $$1$$ bar pressure and $${100^ \circ }C$$ (Given : molar enthalpy of vapourisation of water at $$1$$ bar and $$373$$ $$K$$ $$ = 41\,kJ\,mo{l^{ - 1}}\,$$
and $$R = 8.3\,J\,mo{l^{ - 1}}\,{K^{ - 1}}$$ )
and $$R = 8.3\,J\,mo{l^{ - 1}}\,{K^{ - 1}}$$ )
15
The secondary structure of a protein refers to
16
In the chemical reaction,
CH3CH2NH2 + CHCl3 + 3KOH $$\to$$ (A) + (B) + 3H2O, the compound (A) and (B) are respectively
CH3CH2NH2 + CHCl3 + 3KOH $$\to$$ (A) + (B) + 3H2O, the compound (A) and (B) are respectively
17
Which one of the following is the strongest base in aqueous solution?
18
In the following sequence of reactions,
CH3CH2OH $$\buildrel {P + {I_2}} \over \longrightarrow $$ A $$\mathrel{\mathop{\kern0pt\longrightarrow} \limits_{ether}^{Mg}} $$ B $$\buildrel {HCHO} \over \longrightarrow $$ C $$\buildrel {{H_2}O} \over \longrightarrow $$ D
the compound ‘D’ is
CH3CH2OH $$\buildrel {P + {I_2}} \over \longrightarrow $$ A $$\mathrel{\mathop{\kern0pt\longrightarrow} \limits_{ether}^{Mg}} $$ B $$\buildrel {HCHO} \over \longrightarrow $$ C $$\buildrel {{H_2}O} \over \longrightarrow $$ D
the compound ‘D’ is
19
Which of the following is the correct order of decreasing SN2 reactivity?
20
Which one of the following has a square planar geometry?
21
Identify the incorrect statement among the following :
22
Regular use of which of the following fertilizer increases the acidity of soil?
23
Which of the following nuclear reactions will generate an isotope?
24
A radioactive element gets spilled over the floor of a room. Its half-life period is 30 days. If the initial
activity is ten times the permissible value, after how many days will it be safe to enter the room?
25
Consider the reaction, 2A + B $$\to$$ products. When concentration of B alone was doubled, the half-life did not change. When the concentration of A
alone was doubled, the rate increased by two times. The unit of rate constant for this reaction is
26
The energies of activation for forward and reverse reactions for A2 + B2 $$\leftrightharpoons$$ 2AB are 180 kJ mol−1
and 200 kJ mol−1 respectively. The presence of catalyst lowers the activation energy of both (forward and reverse) reactions by 100 kJ mol−1. The enthalpy change of the reaction ( A2 + B2 $$\to$$ 2AB) in the presence of catalyst will be (in kJ mol−1)
27
The cell, Zn | Zn2+ (1M) || Cu2+ (1M) | Cu($$E_{cell}^o$$ = 1.10V) was allowed to be completely discharged at 298 K. The relative concentration of Zn2+ to Cu2+ $$\left[ {{{\left[ {Z{n^{2 + }}} \right]} \over {\left[ {C{u^{2 + }}} \right]}}} \right]$$ is
28
The equivalent conductances of two strong electrolytes at infinite dilution in H2O (where ions move
freely through a solution) at 25oC are given below:
$$ \wedge _{C{H_3}COONa}^o$$ = 91.0 S cm2/equiv
$$ \wedge _{HCl}^o$$ = 426.2 S cm2/equiv
What additional information/quantity one needs to calculate $$ \wedge ^o$$ of an aqueous solution of acetic acid?
$$ \wedge _{C{H_3}COONa}^o$$ = 91.0 S cm2/equiv
$$ \wedge _{HCl}^o$$ = 426.2 S cm2/equiv
What additional information/quantity one needs to calculate $$ \wedge ^o$$ of an aqueous solution of acetic acid?
29
A mixture of ethyl alcohol and propyl alcohol has a vapour pressure of 290 mm at 300 K. The vapour
pressure of propyl alcohol is 200 mm. If the mole fraction of ethyl alcohol is 0.6, its vapour pressure
(in mm) at the same temperature will be
30
A 5.25 % solution of a substance is isotonic with a 1.5% solution of urea (molar mass = 60 g mol−1) in
the same solvent. If the densities of both the solutions are assumed to be equal to 1.0 g cm−3, molar mass of the substance will be
31
The reaction of toluene with Cl2 in presence of FeCl3 gives predominantly
32
Which of the following hydrogen bonds is the strongest?
33
In which of the following ionization processes, the bond order has increased and the magnetic
behaviour has changed?
34
The charge/size ratio of a cation determines its polarizing power. Which one of the following
sequences represents the increasing order of the polarizinig order of the polarizing power of the
cationic species, K+, Ca2+, Mg2+, Be2+?
35
Which of the following species exhibits the diamagnetic behaviour?
36
Which of the following sets of quantum numbers represents the highest energy of an atom?
37
The density (in g mL-1) of a 3.60 M sulphuric acid solution that is 29% H2SO4 (molar mass = 98 g mol-1) by mass will be
38
In the reaction
2Al(s) + 6HCl(aq) $$\to$$ 2Al3+ (aq) + 6Cl-(aq) + 3H2(g)
2Al(s) + 6HCl(aq) $$\to$$ 2Al3+ (aq) + 6Cl-(aq) + 3H2(g)
Mathematics
1
The average marks of boys in a class is 52 and that of girls is 42. The average marks of boys
and girls combined is 50. The percentage of boys in the class is
2
The function $$f:R/\left\{ 0 \right\} \to R$$ given by
$$f\left( x \right) = {1 \over x} - {2 \over {{e^{2x}} - 1}}$$
can be made continuous at $$x$$ = 0 by defining $$f$$(0) as
$$f\left( x \right) = {1 \over x} - {2 \over {{e^{2x}} - 1}}$$
can be made continuous at $$x$$ = 0 by defining $$f$$(0) as
3
Let $$f:R \to R$$ be a function defined by
$$f(x) = \min \left\{ {x + 1,\left| x \right| + 1} \right\}$$, then which of the following is true?
$$f(x) = \min \left\{ {x + 1,\left| x \right| + 1} \right\}$$, then which of the following is true?
4
The largest interval lying in $$\left( { - {\pi \over 2},{\pi \over 2}} \right)$$ for which the function
$$f\left( x \right) = {4^{ - {x^2}}} + {\cos ^{ - 1}}\left( {{x \over 2} - 1} \right)$$$$ + \log \left( {\cos x} \right)$$,
is defined, is
$$f\left( x \right) = {4^{ - {x^2}}} + {\cos ^{ - 1}}\left( {{x \over 2} - 1} \right)$$$$ + \log \left( {\cos x} \right)$$,
is defined, is
5
If sin-1$$\left( {{x \over 5}} \right)$$ + cosec-1$$\left( {{5 \over 4}} \right)$$ = $${\pi \over 2}$$, then the value of x is :
6
If a line makes an angle of $$\pi /4$$ with the positive directions of each of $$x$$-axis and $$y$$-axis, then the angle that the line makes with the positive direction of the $$z$$-axis is :
7
Two aeroplanes $${\rm I}$$ and $${\rm I}$$$${\rm I}$$ bomb a target in succession. The probabilities of $${\rm I}$$ and $${\rm I}$$$${\rm I}$$ scoring a hit correctly are $$0.3$$ and $$0.2,$$ respectively. The second plane will bomb only if the first misses the target. The probability that the target is hit by the second plane is :
8
Let $$I = \int\limits_0^1 {{{\sin x} \over {\sqrt x }}dx} $$ and $$J = \int\limits_0^1 {{{\cos x} \over {\sqrt x }}dx} .$$ Then which one of the following is true?
9
The area enclosed between the curves $${y^2} = x$$ and $$y = \left| x \right|$$ is :
10
The solution for $$x$$ of the equation $$\int\limits_{\sqrt 2 }^x {{{dt} \over {t\sqrt {{t^2} - 1} }} = {\pi \over 2}} $$ is
11
Let $$F\left( x \right) = f\left( x \right) + f\left( {{1 \over x}} \right),$$ where $$f\left( x \right) = \int\limits_l^x {{{\log t} \over {1 + t}}dt,} $$ Then $$F(e)$$ equals
12
$$\int {{{dx} \over {\cos x + \sqrt 3 \sin x}}} $$ equals
13
If $$D = \left| {\matrix{
1 & 1 & 1 \cr
1 & {1 + x} & 1 \cr
1 & 1 & {1 + y} \cr
} } \right|$$ for $$x \ne 0,y \ne 0,$$ then $$D$$ is :
14
If $$p$$ and $$q$$ are positive real numbers such that $${p^2} + {q^2} = 1$$, then the maximum value of $$(p+q)$$ is
15
The function $$f\left( x \right) = {\tan ^{ - 1}}\left( {\sin x + \cos x} \right)$$ is an incresing function in
16
If $$\widehat u$$ and $$\widehat v$$ are unit vectors and $$\theta $$ is the acute angle between them, then $$2\widehat u \times 3\widehat v$$ is a unit vector for :
17
For the Hyperbola $${{{x^2}} \over {{{\cos }^2}\alpha }} - {{{y^2}} \over {{{\sin }^2}\alpha }} = 1$$ , which of the following remains constant when $$\alpha $$ varies$$=$$?
18
Let A $$\left( {h,k} \right)$$, B$$\left( {1,1} \right)$$ and C $$(2, 1)$$ be the vertices of a right angled triangle with AC as its hypotenuse. If the area of the triangle is $$1$$ square unit, then the set of values which $$'k'$$ can take is given by :
19
In a geometric progression consisting of positive terms, each term equals the sum of the next two terns. Then the common ratio of its progression is equals
20
The set S = {1, 2, 3, ........., 12} is to be partitioned into three sets A, B, C of equal size. Thus $$A \cup B \cup C = S,\,A \cap B = B \cap C = A \cap C = \phi $$. The number of ways to partition S is
21
In the binomial expansion of $${\left( {a - b} \right)^n},\,\,\,n \ge 5,$$ the sum of $${5^{th}}$$ and $${6^{th}}$$ terms is zero, then $$a/b$$ equals
22
If the difference between the roots of the equation $${x^2} + ax + 1 = 0$$ is less than $$\sqrt 5 ,$$ then the set of possible values of $$a$$ is
23
If $$\,\left| {z + 4} \right|\,\, \le \,\,3\,$$, then the maximum value of $$\left| {z + 1} \right|$$ is :
24
Let $$L$$ be the line of intersection of the planes $$2x+3y+z=1$$ and $$x+3y+2z=2.$$ If $$L$$ makes an angle $$\alpha $$ with the positive $$x$$-axis, then cos $$\alpha $$ equals
Physics
1
If $${M_O}$$ is the mass of an oxygen isotope $${}_8{O^{17}}$$ , $${M_p}$$ and $${M_N}$$ are the masses of a proton and neutron respectively, the nuclear binding energy of the isotope is
2
If in a $$p$$-$$n$$ junction diode, a square input signal of $$10$$ $$V$$ is applied as shown


Then the output signal across $${R_L}$$ will be
3
Carbon, silicon and germanium have four valence electrons each. At room temperature which one of the following statements is most appropriate ?
4
Which of the following transitions in hydrogen atoms emit photons of highest frequency ?
5
Photon of frequency $$v$$ has a momentum associated with it. If $$c$$ is the velocity of light, the momentum is
6
Two lenses of power $$-15$$ $$D$$ and $$+5$$ $$D$$ are in contact with each other. The focal length of the combination is
7
In a Young's double slit experiment the intensity at a point where the path difference is $${\lambda \over 6}$$ ( $$\lambda $$ being the wavelength of light used ) is $$I$$. If $${I_0}$$ denotes the maximum intensity, $${I \over {{I_0}}}$$ is equal to
8
An ideal coil of $$10H$$ is connected in series with a resistance of $$5\Omega $$ and a battery of $$5V$$. $$2$$ second after the connection is made, the current flowing in ampere in the circuit is
9
In an $$a.c.$$ circuit the voltage applied is $$E = {E_0}\,\sin \,\omega t.$$ The resulting current in the circuit is $$I = {I_0}\sin \left( {\omega t - {\pi \over 2}} \right).$$ The power consumption in the circuit is given by
10
Two identical conducting wires $$AOB$$ and $$COD$$ are placed at right angles to each other. The wire $$AOB$$ carries an electric current $${I_1}$$ and $$COD$$ carries a current $${I_2}$$. The magnetic field on a point lying at a distance $$d$$ from $$O$$, in a direction perpendicular to the plane of the wires $$AOB$$ and $$COD$$ , will be given by
11
A charged particle moves through a magnetic field perpendicular to its direction. Then
12
A long straight wire of radius $$a$$ carries a steady current $$i.$$ The current is uniformly distributed across its cross section. The ratio of the magnetic field at $$a/2$$ and $$2a$$ is
13
A current $$I$$ flows along the length of an infinitely long, straight, thin walled pipe. Then
14
A charged particle with charge $$q$$ enters a region of constant, uniform and mutually orthogonal fields $$\overrightarrow E $$ and $$\overrightarrow B $$ with a velocity $$\overrightarrow v $$ perpendicular to both $$\overrightarrow E $$ and $$\overrightarrow B, $$ and comes out without any change in magnitude or direction of $$\overrightarrow v $$. Then
15
The resistance of a wire is $$5$$ ohm at $${50^ \circ }C$$ and $$6$$ ohm at $${100^ \circ }C.$$ The resistance of the wire at $${0^ \circ }C$$ will be
16
A battery is used to charge a parallel plate capacitor till the potential difference between the plates becomes equal to the electromotive force of the battery. The ratio of the energy stored in the capacitor and the work done by the battery will be
17
If $${g_E}$$ and $${g_M}$$ are the accelerations due to gravity on the surfaces of the earth and the moon respectively and if Millikan's oil drop experiment could be performed on the two surfaces, one will find the ratio
$${{electro\,\,ch\arg e\,\,on\,\,the\,\,moon} \over {electronic\,\,ch\arg e\,\,on\,\,the\,\,earth}}\,\,to\,be$$
$${{electro\,\,ch\arg e\,\,on\,\,the\,\,moon} \over {electronic\,\,ch\arg e\,\,on\,\,the\,\,earth}}\,\,to\,be$$
18
A parallel plate condenser with a dielectric of dielectric constant $$K$$ between the plates has a capacity $$C$$ and is charged to a potential $$V$$ volt. The dielectric slab is slowly removed from between the plates and then reinserted. The net work done by the system in this process is
19
Charges are placed on the vertices of a square as shown. Let $$\overrightarrow E $$ be the electric field and $$V$$ the potential at the center. If the charges on $$A$$ and $$B$$ are interchanged with those on $$D$$ and $$C$$ respectively, then


20
The potential at a point $$x$$ (measured in $$\mu \,m$$) due to some charges situated on the $$x$$-axis is given by $$V\left( x \right) = 20/\left( {{x^2} - 4} \right)$$ volt
The electric field $$E$$ at $$x = 4\,\mu \,m$$ is given by
The electric field $$E$$ at $$x = 4\,\mu \,m$$ is given by
21
A $$2$$ $$kg$$ block slides on a horizontal floor with a speed of $$4m/s.$$ It strikes a uncompressed spring, and compress it till the block is motionless. The kinetic friction force is $$15N$$ and spring constant is $$10, 000$$ $$N/m.$$ The spring compresses by
22
An electric charge $${10^{ - 3}}\,\,\mu \,C$$ is placed at the origin $$(0,0)$$ of $$X-Y$$ co-ordinate system. Two points $$A$$ and $$B$$ are situated at $$\left( {\sqrt 2 ,\sqrt 2 } \right)$$ and $$\left( {2,0} \right)$$ respectively. The potential difference between the points $$A$$ and $$B$$ will be
23
A sound absorber attenuates the sound level by $$20$$ $$dB$$. The intensity decreases by a factor of
24
The displacement of an object attached to a spring and executing simple harmonic motion is given by $$x = 2 \times {10^{ - 2}}$$ $$cos$$ $$\pi t$$ metre. The time at which the maximum speed first occurs is
25
A point mass oscillates along the $$x$$-axis according to the law $$x = {x_0}\,\cos \left( {\omega t - \pi /4} \right).$$ If the acceleration of the particle is written as $$a = A\,\cos \left( {\omega t + \delta } \right),$$ then
26
Two springs, of force constant $${k_1}$$ and $${k_2}$$ are connected to a mass $$m$$ as shown. The frequency of oscillation of the mass is $$f.$$ If both $${k_1}$$ and $${k_2}$$ are made four times their original values, the frequency of oscillation becomes
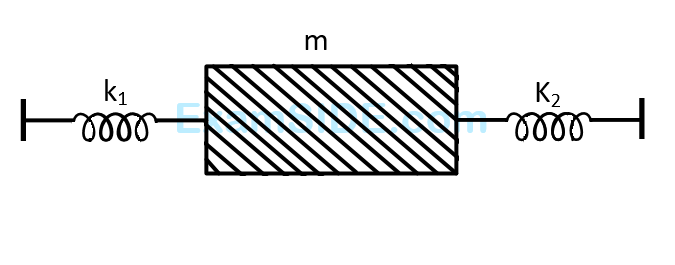

27
A particle of mass $$m$$ executes simple harmonic motion with amplitude a and frequency $$v.$$ The average kinetic energy during its motion from the position of equilibrium to the end is
28
One end of a thermally insulated rod is kept at a temperature $${T_1}$$ and the other at $${T_2}$$. The rod is composed of two sections of length $${L_1}$$ and $${L_2}$$ and thermal conductivities $${K_1}$$ and $${K_2}$$ respectively. The temperature at the interface of the two section is
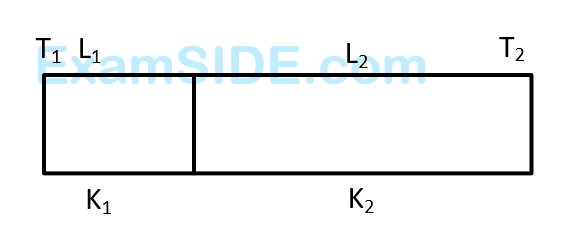

29
When a system is taken from state $$i$$ to state $$f$$ along the path iaf, it is found that $$Q=50$$ cal and $$W=20$$ $$cal$$. Along the path $$ibf$$ $$Q=36$$ $$cal.$$ $$W$$ along the path $$ibf$$ is
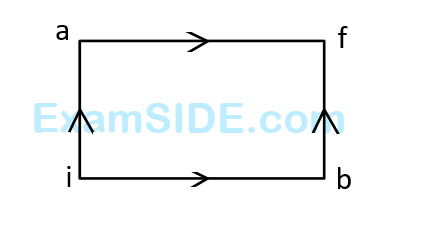

30
For the given uniform square lamina $$ABCD$$, whose center is $$O,$$
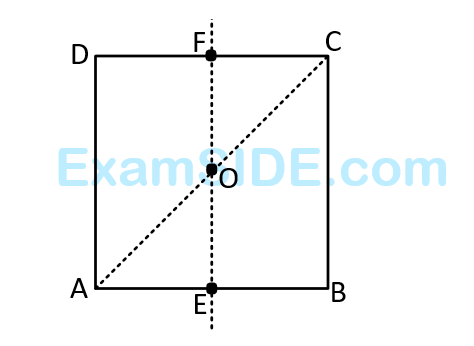

31
If $${C_p}$$ and $${C_v}$$ denote the specific heats of nitrogen per unit mass at constant pressure and constant volume respectively, then
32
Angular momentum of the particle rotating with a central force is constant due to
33
A round uniform body of radius $$R,$$ mass $$M$$ and moment of inertia $$I$$ rolls down (without slipping) an inclined plane making an angle $$\theta $$ with the horizontal. Then its acceleration is
34
A circular disc of radius $$R$$ is removed from a bigger circular disc of radius $$2R$$ such that the circumferences of the discs coincide. The center of mass of the new disc is $$\alpha R$$ form the center of the bigger disc. The value of $$\alpha $$ is
35
A block of mass $$m$$ is connected to another block of $$mass$$ $$M$$ by a spring (massless) of spring constant $$k.$$ The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force $$F$$ starts acting on the block of mass $$M$$ to pull it. Find the force of the block of mass $$m.$$
36
The velocity of a particle is v = v0 + gt + ft2. If its position is x = 0 at t = 0, then its displacement after unit time (t = 1) is
37
A particle is projected at $$60^\circ $$ to the horizontal with a kinetic energy K. The kinetic energy at the
highest point is