The correct match between Item-I (starting material) and Item-II (reagent) for the preparation of benzaldehyde is :

Item-I	Item-II
(I) Benzene	(P) HCl and SnCl2, H3O+
(II) Benzonitrile	(Q) H2, Pd-BaSO4, S and quinoline
(III) Benzoyl Chloride	(R) CO, HCl and AlCl3

The average molar mass of chlorine is 35.5 g mol^–1. The ratio of ³⁵Cl to ³⁷Cl in naturally occuring chlorine is close to :

Mischmetal is an alloy consisting mainly of :

Which of the following compounds can be prepared in good yield by Gabriel phthalimide synthesis?

For a reaction,
4M(s) + nO₂(g) $$ \to $$ 2M₂O_n(s)
the free energy change is plotted as a function of temperature. The temperature below which the oxide is stable could be inferred from the plot as the point at which :

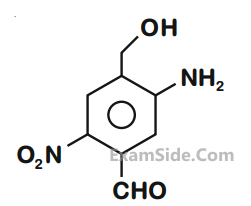
The IUPAC name of the following compound is :

The rate of a reaction decreased by 3.555 times when the temperature was changed from 40^oC to 30^oC. The activation energy (in kJ mol^–1) of the reaction is _______.

Take; R = 8.314 J mol^–1 K^–1 ln 3.555 = 1.268

The atomic number of Unnilunium is _______.

If the solubility product of AB₂ is 3.20 $$ \times $$ 10^–11 M³, then the solubility of AB₂ in pure water is _____ $$ \times $$ 10^–4 mol L^–1.
[Assuming that neither kind of ion reacts with water]

A solution of phenol in chloroform when treated with aqueous NaOH gives compound P as a major product. The mass percentage of carbon in P is ______. (to the nearest integer)
(Atomic mass : C = 12; H = 1; O = 16)

For a d⁴ metal ion in an octahedral field, the correct electronic configuration is :

The increasing order of the boiling points of the major products A, B and C of the following reactions will be :

Match the following :

Test/Method	Reagent
(i) Lucas Test	(a) C6H5SO2Cl/ aq. KOH
(ii) Dumas method	(b) HNO3/ AgNO3
(iii) Kjeldahl’s method	(c) CuO/CO2
(iv) Hinsberg test	(d) Conc. HCl and ZnCl2
	(e) H2SO4

The value of K_C is 64 at 800 K for the reaction

N₂(g) + 3H₂(g) ⇌ 2NH₃(g)

The value of K_C for the following reaction is :

NH₃(g) ⇌ $${1 \over 2}$$N₂(g) + $${3 \over 2}$$H₂(g)

A set of solutions is prepared using 180 g of water as a solvent and 10 g of different nonvolatile solutes A, B and C. The relative lowering of vapour pressure in the presence of these solutes are in the order :

[Given, molar mass of A = 100 g mol^–1; B = 200 g mol^–1; C = 10,000 g mol^–1]

For the given cell :

Cu(s) | Cu²⁺(C₁M) || Cu²⁺(C₂M) | Cu(s)

change in Gibbs energy ($$\Delta $$G) is negative, if :

Which one of the following statements is not true?

For a suitably chosen real constant a, let a

function, $$f:R - \left\{ { - a} \right\} \to R$$ be defined by

$$f(x) = {{a - x} \over {a + x}}$$. Further suppose that for any real number $$x \ne - a$$ and $$f(x) \ne - a$$,

(fof)(x) = x. Then $$f\left( { - {1 \over 2}} \right)$$ is equal to :

Let L denote the line in the xy-plane with x and y intercepts as 3 and 1 respectively. Then the image of the point (–1, –4) in this line is :

The area (in sq. units) of the region enclosed
by the curves y = x² – 1 and y = 1 – x² is equal to :

Let z = x + iy be a non-zero complex number such that $${z^2} = i{\left| z \right|^2}$$, where i = $$\sqrt { - 1} $$ , then z lies on the :

The integral $$\int\limits_1^2 {{e^x}.{x^x}\left( {2 + {{\log }_e}x} \right)} dx$$ equals :

For all twice differentiable functions f : R $$ \to $$ R,
with f(0) = f(1) = f'(0) = 0

Let f : R $$ \to $$ R be a function defined by
f(x) = max {x, x²}. Let S denote the set of all points in R, where f is not differentiable. Then :

The set of all real values of $$\lambda $$ for which the function

$$f(x) = \left( {1 - {{\cos }^2}x} \right)\left( {\lambda + \sin x} \right),x \in \left( { - {\pi \over 2},{\pi \over 2}} \right)$$

has exactly one maxima and exactly one minima, is :

The sum of distinct values of $$\lambda $$ for which the system of equations

$$\left( {\lambda - 1} \right)x + \left( {3\lambda + 1} \right)y + 2\lambda z = 0$$
$$\left( {\lambda - 1} \right)x + \left( {4\lambda - 2} \right)y + \left( {\lambda + 3} \right)z = 0$$
$$2x + \left( {3\lambda + 1} \right)y + 3\left( {\lambda - 1} \right)z = 0$$

has non-zero solutions, is ________ .

Consider the data on x taking the values
0, 2, 4, 8,....., 2ⁿ with frequencies
ⁿC₀ , ⁿC₁ , ⁿC₂ ,...., ⁿC_n respectively. If the
mean of this data is $${{728} \over {{2^n}}}$$, then n is equal to _________ .

If $$\overrightarrow x $$ and $$\overrightarrow y $$ be two non-zero vectors such that $$\left| {\overrightarrow x + \overrightarrow y } \right| = \left| {\overrightarrow x } \right|$$ and $${2\overrightarrow x + \lambda \overrightarrow y }$$ is perpendicular to $${\overrightarrow y }$$, then the value of $$\lambda $$ is _________ .

Suppose that a function f : R $$ \to $$ R satisfies
f(x + y) = f(x)f(y) for all x, y $$ \in $$ R and f(1) = 3.
If $$\sum\limits_{i = 1}^n {f(i)} = 363$$ then n is equal to ________ .

The number of words (with or without meaning) that can be formed from all the letters of the word “LETTER” in which vowels never come together is ________ .

The common difference of the A.P.
b₁, b₂, … , b_m is 2 more than the common
difference of A.P. a₁, a₂, …, a_n. If
a₄₀ = –159, a₁₀₀ = –399 and b₁₀₀ = a₇₀, then b₁ is equal to :

If $$\alpha $$ and $$\beta $$ are the roots of the equation
2x(2x + 1) = 1, then $$\beta $$ is equal to :

The probabilities of three events A, B and C are given by
P(A) = 0.6, P(B) = 0.4 and P(C) = 0.5.
If P(A$$ \cup $$B) = 0.8, P(A$$ \cap $$C) = 0.3, P(A$$ \cap $$B$$ \cap $$C) = 0.2, P(B$$ \cap $$C) = $$\beta $$
and P(A$$ \cup $$B$$ \cup $$C) = $$\alpha $$, where 0.85 $$ \le \alpha \le $$ 0.95, then $$\beta $$ lies in the interval :

If the constant term in the binomial expansion of
$${\left( {\sqrt x - {k \over {{x^2}}}} \right)^{10}}$$ is 405, then |k| equals :

Let $$\theta = {\pi \over 5}$$ and $$A = \left[ {\matrix{ {\cos \theta } & {\sin \theta } \cr { - \sin \theta } & {\cos \theta } \cr } } \right]$$.

If B = A + A⁴ , then det (B) :

Assuming the nitrogen molecule is moving with r.m.s. velocity at 400 K, the de-Broglie wavelength of nitrogen molecule is close to :
(Given : nitrogen molecule weight : 4.64 $$ \times $$ 10^–26 kg,
Boltzman constant: 1.38 $$ \times $$ 10^–23 J/K,
Planck constant : 6.63 $$ \times $$ 10^–34 J.s)

The linear mass density of a thin rod AB of length L varies from A to B as
$$\lambda \left( x \right) = {\lambda _0}\left( {1 + {x \over L}} \right)$$, where x is the distance from A. If M is the mass of the rod then its moment of inertia about an axis passing through A and perpendicular to the rod is :

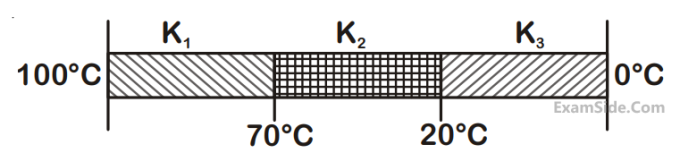
Three rods of identical cross-section and lengths are made of three different materials of thermal conductivity K₁ , K₂ and K₃ , respecrtively. They are joined together at their ends to make a long rod (see figure). One end of the long rod is maintained at 100^oC and the other at 0^oC (see figure). If the joints of the rod are at 70^oC and 20^oC in steady state and there is no loss of energy from the surface of the rod, the correct relationship between K₁ , K₂ and K₃ is :

A fluid is flowing through a horizontal pipe of varying cross-section, with
speed v ms^–1 at a point where the pressure is P pascal. At another point where pressure is $${P \over 2}$$ Pascal its speed is V ms^–1. If the density of the fluid is $$\rho $$ kg m^–3 and the flow is streamline, then V is equal to :

When a particle of mass m is attached to a vertical spring of spring constant k and released, its motion is described by
y(t) = y₀ sin² $$\omega $$t, where 'y' is measured from the lower end of unstretched spring. Then $$\omega $$ is:

In a dilute gas at pressure P and temperature T, the mean time between successive collisions of a molecule varies with T as :

A circuit to verify Ohm's law uses ammeter and voltmeter in series or parallel connected correctly to the resistor. In the circuit :

A square loop of side 2$$a$$ and carrying current I is kept in xz plane with its centre at origin. A long wire carrying the same current I is placed parallel to z-axis and passing through point (0, b, 0), (b >> a). The magnitude of torque on the loop about z-axis will be :

A charged particle going around in a circle can be considered to be a current loop. A particle of mass m carrying charge q is moving in a plane with speed v under the influence of magnetic field $$\overrightarrow B $$. The magnetic moment of this moving particle:

A double convex lens has power P and same radii of curvature R of both the surfaces. The radius of curvature of a surface of a plano-convex lens made of the same material with power 1.5 P is :

When a car is at rest, its driver sees rain drops falling on it vertically. When driving the car with speed v, he sees that rain drops are coming at an angle 60° from the horizontal. On further increasing the speed of the car to (1 + $$\beta $$)v, this angle changes to 45^o. The value of $$\beta $$ is close to :

Particle A of mass m₁ moving with velocity $$\left( {\sqrt3\widehat i + \widehat j} \right)m{s^{ - 1}}$$ collides with another particle B of mass m₂ which is at rest initially. Let $$\overrightarrow {{V_1}} $$ and $$\overrightarrow {{V_2}} $$ be the velocities of particles A and B after collision respectively. If m₁ = 2m₂ and after
collision $$\overrightarrow {{V_1}} = $$$$\left( {\widehat i + \sqrt 3 \widehat j} \right)$$ , the angle between $$\overrightarrow {{V_1}} $$ and $$\overrightarrow {{V_2}} $$ is :

A particle moving in the xy plane experiences a velocity dependent force
$$\overrightarrow F = k\left( {{v_y}\widehat i + {v_x}\widehat j} \right)$$ , where v_x and v_y are the
x and y components of its velocity $$\overrightarrow v $$ . If $$\overrightarrow a $$ is the
acceleration of the particle, then
which of the following statements is true for the particle?

In a series LR circuit, power of 400W is dissipated from a source of 250 V, 50 Hz. The power factor of the circuit is 0.8. In order to bring the power factor to unity, a capacitor of value C is added in series to the L and R. Taking the value of C as $$\left( {{n \over {3\pi }}} \right)$$ $$\mu $$F, then value of n is __________.

A Young's double-slit experiment is performed using monochromatic light of wavelength $$\lambda $$. The intensity of light at a point on the screen, where the path difference is $$\lambda $$, is K units. The intensity of light at a point where the path difference is $${\lambda \over 6}$$ is given by $${{nK} \over {12}}$$, where n is an integer. The value of n is __________.

The centre of mass of solid hemisphere of radius 8 cm is x from the centre of the flat surface. Then value of x is __________.

For a plane electromagnetic wave, the magnetic field at a point x and time t is

$$\overrightarrow B \left( {x,t} \right)$$ = $$\left[ {1.2 \times {{10}^{ - 7}}\sin \left( {0.5 \times {{10}^3}x + 1.5 \times {{10}^{11}}t} \right)\widehat k} \right]$$ T

The instantaneous electric field $$\overrightarrow E $$ corresponding to $$\overrightarrow B $$ is :
(speed of light c = 3 × 10⁸ ms^–1)

Given the masses of various atomic particles
m_p = 1.0072 u, m_n = 1.0087 u, m_e = 0.000548 u,
$${m_{\overline v }}$$ = 0, m_d = 2.0141 u, where p $$ \equiv $$ proton, n $$ \equiv $$ neutron,
e $$ \equiv $$ electron, $$\overline v $$ $$ \equiv $$ antineutrino and d $$ \equiv $$ deuteron. Which of the following process is allowed by momentum and energy conservation?

Two planets have masses M and 16 M and their radii are $$a$$ and 2$$a$$, respectively. The separation between the centres of the planets is 10$$a$$. A body of mass m is fired from the surface of the larger planet towards the smaller planet along the line joining their centres. For the body to be able to reach at the surface of smaller planet, the minimum firing speed needed is :

Consider the force F on a charge 'q' due to a uniformly charged spherical shell of radius R carrying charge Q distributed uniformly over it. Which one of the following statements is true for F, if 'q' is placed at distance r from the centre of the shell?

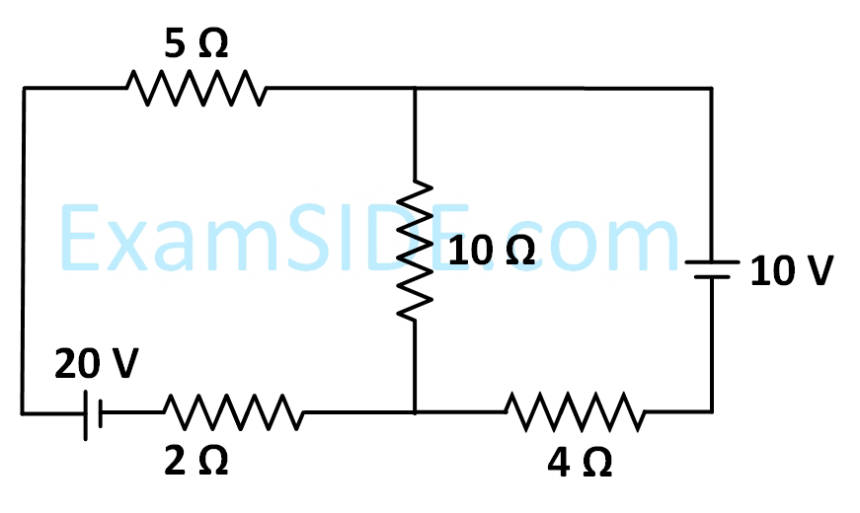
In the figure shown, the current in the 10 V battery is close to :

A student measuring the diameter of a pencil of circular cross-section with the help of a vernier scale records the following four readings 5.50 mm, 5.55 mm, 5.45 mm, 5.65 mm. The average of these four readings is 5.5375 mm and the standard deviation of the data is 0.07395 mm. The average diameter
of the pencil should therefore be recorded as :

Two identical electric point dipoles have dipole moments $${\overrightarrow p _1} = p\widehat i$$ and $${\overrightarrow p _2} = - p\widehat i$$ and are held on the x axis at distance '$$a$$' from each other. When released, they move along the x-axis with the direction of their dipole moments remaining unchanged. If the mass of each dipole is 'm', their speed when they are infinitely far apart is :