JEE Main 2020 (Online) 5th September Evening Slot
Paper was held on
Sat, Sep 5, 2020 9:30 AM
Chemistry
1
The volume, in mL, of 0.02 M K2Cr2O7 solution
required to react with 0.288 g of ferrous
oxalate in acidic medium is _______.
(Molar mass of Fe = 56 g mol–1)
(Molar mass of Fe = 56 g mol–1)
2
For a dimerization reaction,
2A(g) $$ \to $$ A2(g)
at 298 K, $$\Delta $$Uo = –20 kJ mol–1, $$\Delta $$So = –30 JK–1 mol–1,
then the $$\Delta $$Go will be _____ J.
2A(g) $$ \to $$ A2(g)
at 298 K, $$\Delta $$Uo = –20 kJ mol–1, $$\Delta $$So = –30 JK–1 mol–1,
then the $$\Delta $$Go will be _____ J.
3
The number of chiral carbons present in
sucrose is _____.
4
Considering that $$\Delta $$0
> P, the magnetic moment
(in BM) of [Ru(H2O)6]2+ would be _________.
(in BM) of [Ru(H2O)6]2+ would be _________.
5
For a reaction X + Y ⇌ 2Z , 1.0 mol of X, 1.5 mol
of Y and 0.5 mol of Z were taken in a 1 L vessel and
allowed to react. At equilibrium, the concentration
of Z was 1.0 mol L–1. The equilibrium constant of reaction
is $${x \over {15}}$$. The value of x is _________.
of Y and 0.5 mol of Z were taken in a 1 L vessel and
allowed to react. At equilibrium, the concentration
of Z was 1.0 mol L–1. The equilibrium constant of reaction
is $${x \over {15}}$$. The value of x is _________.
6
The increasing order of boiling points of the following compounds is :
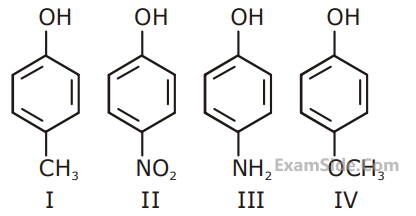

7
The correct order of the ionic radii of
O2–, N3–, F– , Mg2+, Na+ and Al3+ is :
O2–, N3–, F– , Mg2+, Na+ and Al3+ is :
8
Consider the complex ions,
trans-[Co(en)2Cl2]+ (A) and
cis-[Co(en)2Cl2]+ (B).
The correct statement regarding them is :
trans-[Co(en)2Cl2]+ (A) and
cis-[Co(en)2Cl2]+ (B).
The correct statement regarding them is :
9
Lattice enthalpy and enthalpy of solution of NaCl are 788 kJ mol–1, and 4 kJ mol–1, respectively.
The hydration enthalpy of NaCl is :
The hydration enthalpy of NaCl is :
10
Among the following compounds, geometrical isomerism is exhibited by :
11
The major product of the following reaction is :
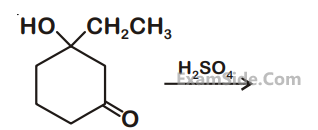

12
The final major product of the following reaction is :
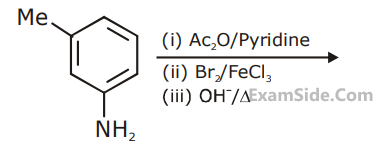
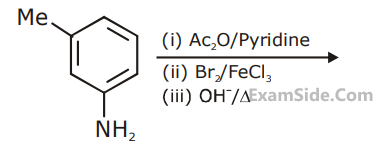
13
The variation of molar conductivity with concentration of an electrolyte (X) in aqueous solution
is shown in the given figure.
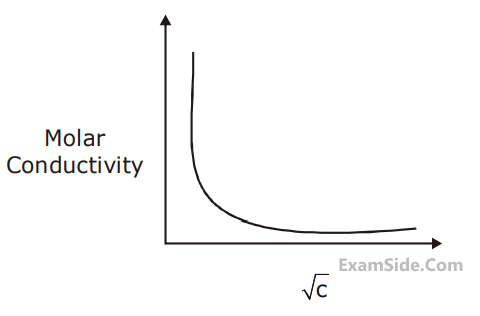
The electrolyte X is :

The electrolyte X is :
14
The rate constant (k) of a reaction is measured at differenct temperatures (T), and the data are
plotted in the given figure. The activation energy of the reaction in kJ mol–1 is :
(R is gas constant)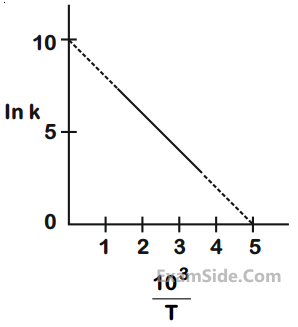
(R is gas constant)

15
The compound that has the largest H–M–H bond angle (M = N, O, S, C) is :
16
The correct statement about probability density (except at infinite distance from nucleus) is :
17
Boron and silicon of very high purity can be obtained through :
18
The major product formed in the following reaction is :
CH3CH = CHCH(CH3)2 $$\buildrel {HBr} \over \longrightarrow $$
CH3CH = CHCH(CH3)2 $$\buildrel {HBr} \over \longrightarrow $$
Mathematics
1
If the mean and the standard deviation of the
data 3, 5, 7, a, b are 5 and 2 respectively, then a and b are the roots of the equation :
data 3, 5, 7, a, b are 5 and 2 respectively, then a and b are the roots of the equation :
2
Let y = y(x) be the solution of the differential
equation
cosx$${{dy} \over {dx}}$$ + 2ysinx = sin2x, x $$ \in $$ $$\left( {0,{\pi \over 2}} \right)$$.
If y$$\left( {{\pi \over 3}} \right)$$ = 0, then y$$\left( {{\pi \over 4}} \right)$$ is equal to :
cosx$${{dy} \over {dx}}$$ + 2ysinx = sin2x, x $$ \in $$ $$\left( {0,{\pi \over 2}} \right)$$.
If y$$\left( {{\pi \over 3}} \right)$$ = 0, then y$$\left( {{\pi \over 4}} \right)$$ is equal to :
3
If the sum of the second, third and fourth terms
of a positive term G.P. is 3 and the sum of its
sixth, seventh and eighth terms is 243, then the
sum of the first 50 terms of this G.P. is :
4
The value of $${\left( {{{ - 1 + i\sqrt 3 } \over {1 - i}}} \right)^{30}}$$ is :
5
If a + x = b + y = c + z + 1, where a, b, c, x, y, z
are non-zero distinct real numbers, then
$$\left| {\matrix{ x & {a + y} & {x + a} \cr y & {b + y} & {y + b} \cr z & {c + y} & {z + c} \cr } } \right|$$ is equal to :
are non-zero distinct real numbers, then
$$\left| {\matrix{ x & {a + y} & {x + a} \cr y & {b + y} & {y + b} \cr z & {c + y} & {z + c} \cr } } \right|$$ is equal to :
6
$$\mathop {\lim }\limits_{x \to 0} {{x\left( {{e^{\left( {\sqrt {1 + {x^2} + {x^4}} - 1} \right)/x}} - 1} \right)} \over {\sqrt {1 + {x^2} + {x^4}} - 1}}$$
7
If the system of linear equations
x + y + 3z = 0
x + 3y + k2z = 0
3x + y + 3z = 0
has a non-zero solution (x, y, z) for some k $$ \in $$ R, then x + $$\left( {{y \over z}} \right)$$ is equal to :
x + y + 3z = 0
x + 3y + k2z = 0
3x + y + 3z = 0
has a non-zero solution (x, y, z) for some k $$ \in $$ R, then x + $$\left( {{y \over z}} \right)$$ is equal to :
8
Let the vectors $$\overrightarrow a $$, $$\overrightarrow b $$, $$\overrightarrow c $$
be such that
$$\left| {\overrightarrow a } \right| = 2$$, $$\left| {\overrightarrow b } \right| = 4$$ and $$\left| {\overrightarrow c } \right| = 4$$. If the projection of
$$\overrightarrow b $$ on $$\overrightarrow a $$ is equal to the projection of $$\overrightarrow c $$ on $$\overrightarrow a $$
and $$\overrightarrow b $$ is perpendicular to $$\overrightarrow c $$, then the value of
$$\left| {\overrightarrow a + \vec b - \overrightarrow c } \right|$$ is ___________.
$$\left| {\overrightarrow a } \right| = 2$$, $$\left| {\overrightarrow b } \right| = 4$$ and $$\left| {\overrightarrow c } \right| = 4$$. If the projection of
$$\overrightarrow b $$ on $$\overrightarrow a $$ is equal to the projection of $$\overrightarrow c $$ on $$\overrightarrow a $$
and $$\overrightarrow b $$ is perpendicular to $$\overrightarrow c $$, then the value of
$$\left| {\overrightarrow a + \vec b - \overrightarrow c } \right|$$ is ___________.
9
The area (in sq. units) of the region
A = {(x, y) : (x – 1)[x] $$ \le $$ y $$ \le $$ 2$$\sqrt x $$, 0 $$ \le $$ x $$ \le $$ 2}, where [t]
denotes the greatest integer function, is :
A = {(x, y) : (x – 1)[x] $$ \le $$ y $$ \le $$ 2$$\sqrt x $$, 0 $$ \le $$ x $$ \le $$ 2}, where [t]
denotes the greatest integer function, is :
10
Let A = {a, b, c} and B = {1, 2, 3, 4}. Then the
number of elements in the set
C = {f : A $$ \to $$ B | 2 $$ \in $$ f(A) and f is not one-one} is ______.
C = {f : A $$ \to $$ B | 2 $$ \in $$ f(A) and f is not one-one} is ______.
11
If L = sin2$$\left( {{\pi \over {16}}} \right)$$ - sin2$$\left( {{\pi \over {8}}} \right)$$ and
M = cos2$$\left( {{\pi \over {16}}} \right)$$ - sin2$$\left( {{\pi \over {8}}} \right)$$, then :
M = cos2$$\left( {{\pi \over {16}}} \right)$$ - sin2$$\left( {{\pi \over {8}}} \right)$$, then :
12
If
$$\int {{{\cos \theta } \over {5 + 7\sin \theta - 2{{\cos }^2}\theta }}} d\theta $$ = A$${\log _e}\left| {B\left( \theta \right)} \right| + C$$,
where C is a constant of integration, then $${{{B\left( \theta \right)} \over A}}$$
can be :
$$\int {{{\cos \theta } \over {5 + 7\sin \theta - 2{{\cos }^2}\theta }}} d\theta $$ = A$${\log _e}\left| {B\left( \theta \right)} \right| + C$$,
where C is a constant of integration, then $${{{B\left( \theta \right)} \over A}}$$
can be :
13
If the length of the chord of the circle,
x2 + y2 = r2 (r > 0) along the line, y – 2x = 3 is r,
then r2 is equal to :
x2 + y2 = r2 (r > 0) along the line, y – 2x = 3 is r,
then r2 is equal to :
14
If $$\alpha $$ and $$\beta $$ are the roots of the equation,
7x2 – 3x – 2 = 0, then the value of
$${\alpha \over {1 - {\alpha ^2}}} + {\beta \over {1 - {\beta ^2}}}$$ is equal to :
7x2 – 3x – 2 = 0, then the value of
$${\alpha \over {1 - {\alpha ^2}}} + {\beta \over {1 - {\beta ^2}}}$$ is equal to :
15
The derivative of
$${\tan ^{ - 1}}\left( {{{\sqrt {1 + {x^2}} - 1} \over x}} \right)$$ with
respect to $${\tan ^{ - 1}}\left( {{{2x\sqrt {1 - {x^2}} } \over {1 - 2{x^2}}}} \right)$$ at x = $${1 \over 2}$$ is :
$${\tan ^{ - 1}}\left( {{{\sqrt {1 + {x^2}} - 1} \over x}} \right)$$ with
respect to $${\tan ^{ - 1}}\left( {{{2x\sqrt {1 - {x^2}} } \over {1 - 2{x^2}}}} \right)$$ at x = $${1 \over 2}$$ is :
16
If x = 1 is a critical point of the function
f(x) = (3x2 + ax – 2 – a)ex , then :
f(x) = (3x2 + ax – 2 – a)ex , then :
17
There are 3 sections in a question paper and
each section contains 5 questions. A candidate
has to answer a total of 5 questions, choosing
at least one question from each section. Then
the number of ways, in which the candidate
can choose the questions, is :
Physics
1
Nitrogen gas is at 300oC temperature. The
temperature (in K) at which the rms speed of a
H2 molecule would be equal to the rms speed
of a nitrogen molecule, is _______.
(Molar mass of N2 gas 28 g).
(Molar mass of N2 gas 28 g).
2
In an experiment to verify Stokes law, a small
spherical ball of radius r and density $$\rho $$ falls
under gravity through a distance h in air before
entering a tank of water. If the terminal velocity
of the ball inside water is same as its velocity
just before entering the water surface, then the
value of h is proportional to :
(ignore viscosity of air)
(ignore viscosity of air)
3
Two coherent sources of sound, S1 and S2,
produce sound waves of the same wavelength,
$$\lambda $$ = 1 m, in phase. S1 and S2 are placed 1.5 m
apart (see fig). A listener, located at L, directly
in front of S2 finds that the intensity is at a
minimum
when he is 2 m away from S2. The listener moves away from S1, keeping his distance from S2 fixed. The adjacent maximum of intensity is observed when the listener is at a distance d from S1. Then, d is :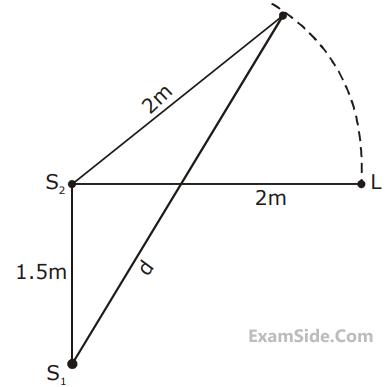
when he is 2 m away from S2. The listener moves away from S1, keeping his distance from S2 fixed. The adjacent maximum of intensity is observed when the listener is at a distance d from S1. Then, d is :

4
The velocity (v) and time (t) graph of a body in
a straight line motion is shown in the figure.
The point S is at 4.333 seconds. The total
distance covered by the body in 6 s is :
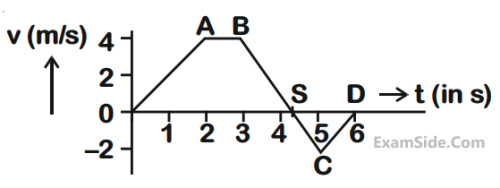

5
A galvanometer is used in laboratory for
detecting the null point in electrical
experiments. If, on passing a current of 6 mA it
produces a deflection of 2o, its figure of merit
is close to :
6
A parallel plate capacitor has plate of length
'l', width ‘w’ and separation of plates is ‘d’. It
is connected to a battery of emf V. A dielectric
slab of the same thickness ‘d’ and of dielectric
constant k = 4 is being inserted between the
plates of the capacitor. At what length of the
slab inside plates, will the energy stored in the
capacitor be two times the initial energy
stored?
7
The acceleration due to gravity on the earth’s
surface at the poles is g and angular velocity of
the earth about the axis passing through the
pole is $$\omega $$. An object is weighed at the equator
and at a height h above the poles by using a
spring balance. If the weights are found to be
same, then h is (h << R, where R is the radius
of the earth)
8
In an adiabatic process, the density of a
diatomic gas becomes 32 times its initial value.
The final pressure of the gas is found to be n
times the initial pressure. The value of n is :
9
An iron rod of volume 10–3 m3 and relative
permeability 1000 is placed as core in a
solenoid with 10 turns/cm. If a current of 0.5 A
is passed through the solenoid, then the
magnetic moment of the rod will be :
10
A thin rod of mass 0.9 kg and length 1 m is
suspended, at rest, from one end so that it can
freely oscillate in the vertical plane. A particle
of move 0.1 kg moving in a straight line with
velocity 80 m/s hits the rod at its bottom most
point and sticks to it (see figure). The angular
speed (in rad/s) of the rod immediately after the
collision will be _________.


11
In the circuit, given in the figure currents in
different branches and value of one resistor are
shown. Then potential at point B with respect to
the point A is :
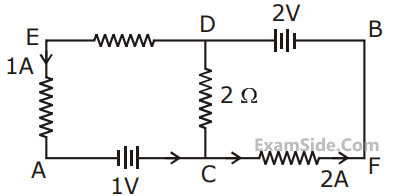

12
Two Zener diodes (A and B) having breakdown
voltages of 6 V and 4 V respectively, are
connected as shown in the circuit below. The
output voltage V0 variation with input voltage
linearly increasing with time, is given by :
(Vinput = 0 V at t = 0)
(figures are qualitative)
(Vinput = 0 V at t = 0)
(figures are qualitative)

13
Two different wires having lengths L1 and L2,
and respective temperature coefficient of linear
expansion $$\alpha $$1 and $$\alpha $$2, are joined end-to-end.
Then the effective temperature coefficient of
linear expansion is :
14
The correct match between the entries in
column I and column II are :
| I | II |
|---|---|
| Radiation | Wavelength |
| (a) Microwave | (i) 100 m |
| (b) Gamma rays | (ii) 10–15 m |
| (c) A.M. radio waves | (iii) 10–10 m |
| (d) X-rays | (iv) 10–3 m |
15
Ten charges are placed on the circumference
of a circle of radius R with constant angular
separation between successive charges.
Alternate charges 1, 3, 5, 7, 9 have charge (+q)
each, while 2, 4, 6, 8, 10 have charge (–q) each.
The potential V and the electric field E at the
centre of the circle are respectively.
(Take V = 0 at infinity)
(Take V = 0 at infinity)
16
The quantities x = $${1 \over {\sqrt {{\mu _0}{\varepsilon _0}} }}$$, y = $${E \over B}$$ and z = $${l \over {CR}}$$ are
defined where C-capacitance, R-Resistance, l-length, E-Electric field, B-magnetic field and $${{\varepsilon _0}}$$, $${{\mu _0}}$$, - free space permittivity and permeability respectively. Then :
defined where C-capacitance, R-Resistance, l-length, E-Electric field, B-magnetic field and $${{\varepsilon _0}}$$, $${{\mu _0}}$$, - free space permittivity and permeability respectively. Then :
17
A ring is hung on a nail. It can oscillate, without
slipping or sliding
(i) in its plane with a time period T1 and,
(ii) back and forth in a direction perpendicular to its plane,
with a period T2. The ratio $${{{T_1}} \over {{T_2}}}$$ will be :
(i) in its plane with a time period T1 and,
(ii) back and forth in a direction perpendicular to its plane,
with a period T2. The ratio $${{{T_1}} \over {{T_2}}}$$ will be :
18
A spaceship in space sweeps stationary
interplanetary dust. As a result, its mass
increases at a rate $${{dM\left( t \right)} \over {dt}}$$ = bv2(t), where v(t) is its instantaneous velocity. The instantaneous acceleration of the satellite is :
increases at a rate $${{dM\left( t \right)} \over {dt}}$$ = bv2(t), where v(t) is its instantaneous velocity. The instantaneous acceleration of the satellite is :
19
A body of mass 2 kg is driven by an engine
delivering a constant power of 1 J/s. The body
starts from rest and moves in a straight line.
After 9 seconds, the body has moved a
distance (in m) _______.
20
The surface of a metal is illuminated alternately
with photons of energies E1 = 4 eV and E2 = 2.5 eV
respectively. The ratio of maximum speeds of the
photoelectrons emitted in the two cases is 2. The
work function of the metal in (eV) is _____.
21
A prism of angle A = 1o has a refractive index
$$\mu $$ = 1.5. A good estimate for the minimum angle
of deviation (in degrees) is close to $${N \over {10}}$$.
Value of N is ____.
Value of N is ____.
22
In the circuit shown, charge on the 5 $$\mu $$F
capacitor is :


23
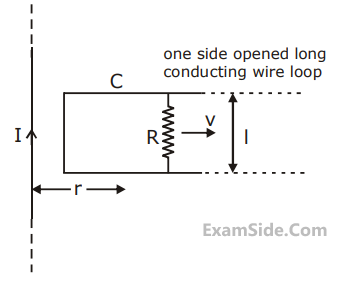
An infinitely long, straight wire carrying current
I, one side opened rectangular loop and a
conductor C with a sliding connector are
located in the same plane, as shown, in the
figure. The connector has length $$l$$ and
resistance R. It slides to the right with a
velocity v. The resistance of the conductor and
the self inductance of the loop are negligible.
The induced current in the loop, as a function
of separation r, between the connector and the
straight wire is :