JEE Main 2020 (Online) 7th January Evening Slot
Paper was held on
Tue, Jan 7, 2020 9:30 AM
Chemistry
1
Two open beakers one containing a solvent and the other containing a mixture of that solvent
with a non voltatile solute are together selated in a container. Over time :
2
Among the statements(a)-(d) the incorrect ones are :
(a) Octahedral CO(III) complexes with strong fields ligands have very high magnetic moments.
(b) When $$\Delta $$0 < P, the d-electron configuration of Co(III) in an octahedral complex is $$t_{eg}^4e_g^2$$
(c) Wavelength of light absorbed by [Co(en)3]3+ is lower than that of [CoF6]3-
(d) If the $$\Delta $$0 for an octahedral complex of CO(III) is 18,000 cm-1, the $$\Delta $$t for its tetrahedral complex with the same ligand be 16,000 cm-1
(a) Octahedral CO(III) complexes with strong fields ligands have very high magnetic moments.
(b) When $$\Delta $$0 < P, the d-electron configuration of Co(III) in an octahedral complex is $$t_{eg}^4e_g^2$$
(c) Wavelength of light absorbed by [Co(en)3]3+ is lower than that of [CoF6]3-
(d) If the $$\Delta $$0 for an octahedral complex of CO(III) is 18,000 cm-1, the $$\Delta $$t for its tetrahedral complex with the same ligand be 16,000 cm-1
3
In the following reaction sequence,

The major product B is :

The major product B is :
4
The ammonia (NH3) released on quantitative reaction of 0.6 g urea (NH2CONH2) with sodium hydroxide (NaOH) can be neutralized by :
5
Within each pair of elements F & Cl, S & Se, and Li & Na, respectively, the elements that release
more energy upon and electron gain are :
6
Which of the following statements is correct ?
7
A chromatography column, packed with silica gel as stationary phase, was used to separate a
mixture of compounds consisting of (A) benzanilide (B) aniline and (C) acetophenone. When the
column is eluted with a mixture of solvents, hexane : ethylacelate (20:80), the sequence of
obtained compounds is :
8
The redox reaction among the following is :
9
In the following reactions sequence, structure of A and B respectively will be :


10
For the following reactions

Ks and Ke, are respectively, the rate constants for substitution and elimination and $$\mu = {{{k_s}} \over {{k_e}}}$$ the correct options is

Ks and Ke, are respectively, the rate constants for substitution and elimination and $$\mu = {{{k_s}} \over {{k_e}}}$$ the correct options is
11
The number of possible optical isomers for the complexes MA2B2 with sp3 and dsp2 hydridized metal atom. respectively, is :
Note : A and B are unidentate netural and unidentate monoanionic ligands, respectively.
Note : A and B are unidentate netural and unidentate monoanionic ligands, respectively.
12
The bond order and the magnetic characteristics of CN-
are :
13
The equation that is incorrect is :
14
The correct order of stability for the following alkoxides is :


15
For the reaction
2H2(g) + 2NO(g) $$ \to $$ N2(g) + 2H2O(g)
the observed rate expression is, rate = Kf[NO]2[H2]. The rate expression for the reverse reaction is :
2H2(g) + 2NO(g) $$ \to $$ N2(g) + 2H2O(g)
the observed rate expression is, rate = Kf[NO]2[H2]. The rate expression for the reverse reaction is :
16
Consider the following reactions :




Which of these reactions are possible ?




Which of these reactions are possible ?
17
The flocculation value of HCl for arsenic sulphide sol.
is 30 m mol L-1 If H2SO4 is used for the flocculatiopn of arsenic sulphide, the amount in grams, of H2SO4 in 250 ml required for the above purposed is ______.
(molecular mass of H2SO4 = 98 g/mol)
is 30 m mol L-1 If H2SO4 is used for the flocculatiopn of arsenic sulphide, the amount in grams, of H2SO4 in 250 ml required for the above purposed is ______.
(molecular mass of H2SO4 = 98 g/mol)
18
3 g of acetic acid is added to 250 mL of 0.1 M HCL and the solution made up to 500 mL. To 20 mL
of this solutions $${1 \over 2}$$ mL of 5 M NaOH is added. The pH of the solution is __________.
[Given : pKa of acetic acid = 4.75, molar mass of acetic of acid = 60 g/mol, log 3 = 0.4771] Neglect any changes in volume.
[Given : pKa of acetic acid = 4.75, molar mass of acetic of acid = 60 g/mol, log 3 = 0.4771] Neglect any changes in volume.
19
The standard heat of formation $$\left( {{\Delta _f}H_{298}^0} \right)$$ of ethane (in kj/mol), if the heat of combustion of
ethane, hydrogen and graphite are - 1560, -393.5 and -286 Kj/mol, respectively is :
20
Consider the following reactions :
$$NaCl{\rm{ }} + {\rm{ }}{K_2}C{r_2}{O_7} + \mathop {{H_2}S{O_4}}\limits_{(conc.)} $$$$ \to $$ (A) + side products
(A) + NaOH $$ \to $$ (B) + Side products
$$\left( B \right){\rm{ }} + \mathop {{H_2}S{O_4}}\limits_{(dilute)} + {\rm{ }}{H_2}{O_2}$$ $$ \to $$ (C) + Side products
The sum of the total number of atoms in one molecule each of (A) and (B) and (C) is
$$NaCl{\rm{ }} + {\rm{ }}{K_2}C{r_2}{O_7} + \mathop {{H_2}S{O_4}}\limits_{(conc.)} $$$$ \to $$ (A) + side products
(A) + NaOH $$ \to $$ (B) + Side products
$$\left( B \right){\rm{ }} + \mathop {{H_2}S{O_4}}\limits_{(dilute)} + {\rm{ }}{H_2}{O_2}$$ $$ \to $$ (C) + Side products
The sum of the total number of atoms in one molecule each of (A) and (B) and (C) is
Mathematics
1
Let $${a_1}$$
, $${a_2}$$
, $${a_3}$$
,....... be a G.P. such that
$${a_1}$$ < 0, $${a_1}$$ + $${a_2}$$ = 4 and $${a_3}$$ + $${a_4}$$ = 16.
If $$\sum\limits_{i = 1}^9 {{a_i}} = 4\lambda $$, then $$\lambda $$ is equal to:
$${a_1}$$ < 0, $${a_1}$$ + $${a_2}$$ = 4 and $${a_3}$$ + $${a_4}$$ = 16.
If $$\sum\limits_{i = 1}^9 {{a_i}} = 4\lambda $$, then $$\lambda $$ is equal to:
2
The coefficient of x7
in the expression
(1 + x)10 + x(1 + x)9 + x2(1 + x)8 + ......+ x10 is:
(1 + x)10 + x(1 + x)9 + x2(1 + x)8 + ......+ x10 is:
3
The number of ordered pairs (r, k) for which
6.35Cr = (k2 - 3). 36Cr + 1, where k is an integer, is :
6.35Cr = (k2 - 3). 36Cr + 1, where k is an integer, is :
4
The value of $$\alpha $$ for which
$$4\alpha \int\limits_{ - 1}^2 {{e^{ - \alpha \left| x \right|}}dx} = 5$$, is:
$$4\alpha \int\limits_{ - 1}^2 {{e^{ - \alpha \left| x \right|}}dx} = 5$$, is:
5
The locus of the mid-points of the perpendiculars drawn from points on the line, x = 2y to the line
x = y is :
6
If the function ƒ defined on $$\left( { - {1 \over 3},{1 \over 3}} \right)$$ by
f(x) = $$\left\{ {\matrix{ {{1 \over x}{{\log }_e}\left( {{{1 + 3x} \over {1 - 2x}}} \right),} & {when\,x \ne 0} \cr {k,} & {when\,x = 0} \cr } } \right.$$
is continuous, then k is equal to_______.
f(x) = $$\left\{ {\matrix{ {{1 \over x}{{\log }_e}\left( {{{1 + 3x} \over {1 - 2x}}} \right),} & {when\,x \ne 0} \cr {k,} & {when\,x = 0} \cr } } \right.$$
is continuous, then k is equal to_______.
7
If the mean and variance of eight numbers 3, 7, 9, 12, 13, 20, x and y be 10 and 25 respectively,
then x.y is equal to _______.
8
If the system of linear equations,
x + y + z = 6
x + 2y + 3z = 10
3x + 2y + $$\lambda $$z = $$\mu $$
has more than two solutions, then $$\mu $$ - $$\lambda $$2 is equal to ______.
x + y + z = 6
x + 2y + 3z = 10
3x + 2y + $$\lambda $$z = $$\mu $$
has more than two solutions, then $$\mu $$ - $$\lambda $$2 is equal to ______.
9
If the foot of the perpendicular drawn from the point (1, 0, 3) on a line passing through ($$\alpha $$, 7, 1)
is
$$\left( {{5 \over 3},{7 \over 3},{{17} \over 3}} \right)$$, then $$\alpha $$ is equal to______.
10
Let ƒ(x) be a polynomial of degree 5 such that x = ±1 are its critical points.
If $$\mathop {\lim }\limits_{x \to 0} \left( {2 + {{f\left( x \right)} \over {{x^3}}}} \right) = 4$$, then which one of the following is not true?
If $$\mathop {\lim }\limits_{x \to 0} \left( {2 + {{f\left( x \right)} \over {{x^3}}}} \right) = 4$$, then which one of the following is not true?
11
Let X = {n $$ \in $$ N : 1 $$ \le $$ n $$ \le $$ 50}. If
A = {n $$ \in $$ X: n is a multiple of 2} and
B = {n $$ \in $$ X: n is a multiple of 7}, then the number of elements in the smallest subset of X containing both A and B is ________.
A = {n $$ \in $$ X: n is a multiple of 2} and
B = {n $$ \in $$ X: n is a multiple of 7}, then the number of elements in the smallest subset of X containing both A and B is ________.
12
If $${{3 + i\sin \theta } \over {4 - i\cos \theta }}$$, $$\theta $$ $$ \in $$ [0, 2$$\theta $$], is a real number, then an argument of
sin$$\theta $$ + icos$$\theta $$ is :
sin$$\theta $$ + icos$$\theta $$ is :
13
If $$\theta $$1
and $$\theta $$2
be respectively the smallest and the largest values of $$\theta $$ in (0, 2$$\pi $$) - {$$\pi $$} which satisfy
the equation,
2cot2$$\theta $$ - $${5 \over {\sin \theta }}$$ + 4 = 0, then
$$\int\limits_{{\theta _1}}^{{\theta _2}} {{{\cos }^2}3\theta d\theta } $$ is equal to :
2cot2$$\theta $$ - $${5 \over {\sin \theta }}$$ + 4 = 0, then
$$\int\limits_{{\theta _1}}^{{\theta _2}} {{{\cos }^2}3\theta d\theta } $$ is equal to :
14
Let y = y(x) be a function of x satisfying
$$y\sqrt {1 - {x^2}} = k - x\sqrt {1 - {y^2}} $$ where k is a constant and
$$y\left( {{1 \over 2}} \right) = - {1 \over 4}$$. Then $${{dy} \over {dx}}$$ at x = $${1 \over 2}$$, is equal to :
$$y\sqrt {1 - {x^2}} = k - x\sqrt {1 - {y^2}} $$ where k is a constant and
$$y\left( {{1 \over 2}} \right) = - {1 \over 4}$$. Then $${{dy} \over {dx}}$$ at x = $${1 \over 2}$$, is equal to :
15
Let $$\overrightarrow a $$
, $$\overrightarrow b $$
and $$\overrightarrow c $$
be three unit vectors such that
$$\overrightarrow a + \vec b + \overrightarrow c = \overrightarrow 0 $$. If $$\lambda = \overrightarrow a .\vec b + \vec b.\overrightarrow c + \overrightarrow c .\overrightarrow a $$ and
$$\overrightarrow d = \overrightarrow a \times \vec b + \vec b \times \overrightarrow c + \overrightarrow c \times \overrightarrow a $$, then the ordered pair, $$\left( {\lambda ,\overrightarrow d } \right)$$ is equal to :
$$\overrightarrow a + \vec b + \overrightarrow c = \overrightarrow 0 $$. If $$\lambda = \overrightarrow a .\vec b + \vec b.\overrightarrow c + \overrightarrow c .\overrightarrow a $$ and
$$\overrightarrow d = \overrightarrow a \times \vec b + \vec b \times \overrightarrow c + \overrightarrow c \times \overrightarrow a $$, then the ordered pair, $$\left( {\lambda ,\overrightarrow d } \right)$$ is equal to :
16
The area (in sq. units) of the region
{(x, y) $$ \in $$ R2 | 4x2 $$ \le $$ y $$ \le $$ 8x + 12} is :
{(x, y) $$ \in $$ R2 | 4x2 $$ \le $$ y $$ \le $$ 8x + 12} is :
17
Let y = y(x) be the solution curve of the differential equation,
$$\left( {{y^2} - x} \right){{dy} \over {dx}} = 1$$, satisfying y(0) = 1. This curve intersects the x-axis at a point whose abscissa is :
$$\left( {{y^2} - x} \right){{dy} \over {dx}} = 1$$, satisfying y(0) = 1. This curve intersects the x-axis at a point whose abscissa is :
18
Let $$\alpha $$ and $$\beta $$ be the roots of the equation x2
- x - 1 = 0.
If pk = $${\left( \alpha \right)^k} + {\left( \beta \right)^k}$$ , k $$ \ge $$ 1, then which one of the following statements is not true?
If pk = $${\left( \alpha \right)^k} + {\left( \beta \right)^k}$$ , k $$ \ge $$ 1, then which one of the following statements is not true?
Physics
1
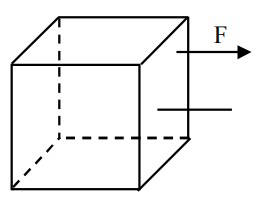 Consider a uniform cubical box of side a on a rough floor that is to be moved by applying
minimum possible force F at a point b above its centre of mass (see figure). If the coefficient of
friction is $$\mu $$ = 0.4, the maximum possible value of 100 × $${b \over a}$$
for box not to topple before moving
is .......
Consider a uniform cubical box of side a on a rough floor that is to be moved by applying
minimum possible force F at a point b above its centre of mass (see figure). If the coefficient of
friction is $$\mu $$ = 0.4, the maximum possible value of 100 × $${b \over a}$$
for box not to topple before moving
is .......2
The sum of two forces $$\overrightarrow P $$
and $$\overrightarrow Q $$
is $$\overrightarrow R $$
such that $$\left| {\overrightarrow R } \right| = \left| {\overrightarrow P } \right|$$
. The angle $$\theta $$ (in degrees) that the
resultant of 2$${\overrightarrow P }$$
and $${\overrightarrow Q }$$
will make with $${\overrightarrow Q }$$
is , ..............
3
M grams of steam at 100oC is mixed with 200 g of ice at its melting point in a thermally insulated
container. If it produced liquid water at 40oC [heat of vaporization of water is 540 cal/g and heat
of fusion of ice is 80 cal/g] the value of M is ____
4
A 60 pF capacitor is fully charged by a 20 V supply. It is then disconnected from the supply and
is conneced to another uncharged 60 pF capacitor in parallel. The electrostatic energy that is lost
in this process by the time the charge is redistributed between them is (in nJ) _____
5
A box weight 196 N on a spring balance at the north pole. Its weight recorded on the same
balance if it is shifted to the equator is close to (Take g = 10 ms–2 at the north pole and the radius
of the earth = 6400 km) :
6
The dimension of $${{{B^2}} \over {2{\mu _0}}}$$, where B is magnetic field and $${{\mu _0}}$$
is the magnetic permeability of vacuum,
is :
7
Under an adiabatic process, the volume of an ideal gas gets doubled. Consequently the mean
collision time between the gas molecule changes from $${\tau _1}$$
to $${\tau _2}$$
. If $${{{C_p}} \over {{C_v}}} = \gamma $$ for this gas then a good
estimate for $${{{\tau _2}} \over {{\tau _1}}}$$
is given by :
8
The electric field of a plane electromagnetic wave is given by
$$\overrightarrow E = {E_0}{{\widehat i + \widehat j} \over {\sqrt 2 }}\cos \left( {kz + \omega t} \right)$$
At t = 0, a positively charged particle is at the point (x, y, z) = $$\left( {0,0,{\pi \over k}} \right)$$.
If its instantaneous velocity at (t = 0) is $${v_0}\widehat k$$ , the force acting on it due to the wave is :
$$\overrightarrow E = {E_0}{{\widehat i + \widehat j} \over {\sqrt 2 }}\cos \left( {kz + \omega t} \right)$$
At t = 0, a positively charged particle is at the point (x, y, z) = $$\left( {0,0,{\pi \over k}} \right)$$.
If its instantaneous velocity at (t = 0) is $${v_0}\widehat k$$ , the force acting on it due to the wave is :
9
In a Young's double slit experiment, the separation between the slits is 0.15 mm. in the experiment,
a source of light of wavelengh 589 nm is used and the interference pattern is observed on a
screen kept 1.5 m away. The separation between the successive bright fringes on the screen is :
10
An elevator in a building can carry a maximum of 10 persons, with the average mass of each
person being 68 kg, The mass of the elevator itself is 920 kg and it moves with a constant speed
of 3 m/s. The frictional force opposing the motion is 6000 N. If the elevator is moving up with its
full capacity, the power delivered by the motor to the elevator (g = 10 m/s2) must be at least :
11
A mass of 10 kg is suspended by a rope of length 4 m, from the ceiling. A force F is applied
horizontally at the mid point of the rope such that the top half of the rope makes an angle of 45o
with the vertical. Then F equal : (Take g = 10 ms–2 and the rope to be massless)
12
In a building there are 15 bulbs of 45 W, 15 bulbs of 100 W, 15 small fans of 10 W and 2 heaters
of 1 kW. The voltage of electric main is 220 V. The minimum fuse capacity (rated value) of the
building will be :
13
In the figure, potential difference between A and B is :


14
An ideal fluid flows (laminar flow) through a pipe of non-uniform diameter. The maximum and
minimum diameters of the pipes are 6.4 cm and 4.8 cm, respectively. The ratio of the minimum
and the maximum velocities of fluid in this pipe is :
15
A thin lens made of glass (refractive index = 1.5) of focal length f = 16 cm is immersed in a liquid
of refractive index 1.42. If its focal length in liquid is f1
, then the ratio $${{{f_1}} \over f}$$ is closest to the
integer :
16
A planar loop of wire rotates in a uniform magnetic field. Initially at t = 0, the plane of the loop
is perpendicular to the magnetic field. If it rotates with a period of 10 s about an axis in its plane
then the magnitude of induced emf will be maximum and minimum, respectively at :
17
An emf of 20 V is applied at time t = 0 to a circuit containing in series 10 mH inductor and 5 $$\Omega $$
resistor. The ratio of the currents at time t = $$\infty $$ and at t = 40 s is close to : (Take e2 = 7.389)
18
A particle of mass m and charge q has an initial velocity $$\overrightarrow v = {v_0}\widehat j$$
. If an electric field $$\overrightarrow E = {E_0}\widehat i$$
and
magnetic field $$\overrightarrow B = {B_0}\widehat i$$
act on the particle, its speed will double after a time:
19
Mass per unit area of a circular disc of radius $$a$$ depends on the distance r from its centre as $$\sigma \left( r \right)$$ = A + Br
. The moment of inertia of the disc about the axis, perpendicular to the plane and
assing through its centre is:
20
An electron (of mass m) and a photon have the same energy E in the range of a few eV. The ratio
of the de-Broglie wavelength associated with the electron and the wavelength of the photon is (c
= speed of light in vaccuum)