JEE Main 2021 (Online) 16th March Morning Shift
Paper was held on
Tue, Mar 16, 2021 3:30 AM
Chemistry
1

The product ''P'' in the above reaction is :
2
Given below are two statements : one is labeled as Assertion A and the other is labelled as Reason R :
Assertion A : The H$$-$$O$$-$$H bond angle in water molecule is 104.5$$^\circ$$.
Reason R : The lone pair - lone pair repulsion of electrons is higher than the bond pair - bond pair repulsion.
In the light of the above statements, choose the correct answer from the options given below :
Assertion A : The H$$-$$O$$-$$H bond angle in water molecule is 104.5$$^\circ$$.
Reason R : The lone pair - lone pair repulsion of electrons is higher than the bond pair - bond pair repulsion.
In the light of the above statements, choose the correct answer from the options given below :
3
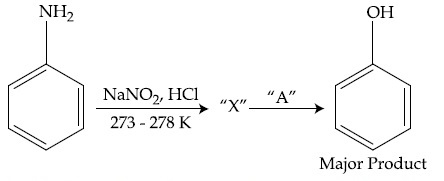
In the above chemical reaction, intermediate ''X'' and reagent/condition ''A'' are :
4
Assertion A : Enol form of acetone [CH3COCH3] exists in < 0.1% quantity. However, the enol form of acetyl acetone [CH3COCH2OCCH3] exists in approximately 15% quantity.
Reason R : Enol form of acetyl acetone is stabilized by intramolecular hydrogen bonding, which is not possible in enol form of acetone.
Choose the correct statement :
Reason R : Enol form of acetyl acetone is stabilized by intramolecular hydrogen bonding, which is not possible in enol form of acetone.
Choose the correct statement :
5
Given below are two statements :
Statement I : The Eo value for Ce4+ / Ce3+ is + 1.74 V.
Statement II : Ce is more stable in Ce4+ state than Ce3+ state.
In the light of the above statements, choose the most appropriate answer from the options given below :
Statement I : The Eo value for Ce4+ / Ce3+ is + 1.74 V.
Statement II : Ce is more stable in Ce4+ state than Ce3+ state.
In the light of the above statements, choose the most appropriate answer from the options given below :
6
In chromotography technique, the purification of compound is independent of :
7
A group of 15 element, which is a metal and forms a hydride with strongest reducing power among group 15 hydrides. The element is :
8
Among the following, the aromatic compounds are :
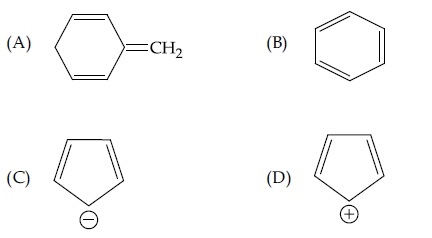
Choose the correct answer from the following options :

Choose the correct answer from the following options :
9
Which of the following reactions DOES NOT involve Hoffmann bromamide degradation?
10
Which of the following is Lindlar catalyst?
11
Which among the following pairs of Vitamins is stored in our body relatively for longer duration?
12
Given below are two statement : one is labelled as Assertion A and the other is labelled as Reason R :
Assertion A : Size of Bk3+ ion is less than Np3+ ion.
Reason R : The above is a consequence of the lanthanoid contraction.
In the light of the above statements, choose the correct answer from the options given below :
Assertion A : Size of Bk3+ ion is less than Np3+ ion.
Reason R : The above is a consequence of the lanthanoid contraction.
In the light of the above statements, choose the correct answer from the options given below :
13
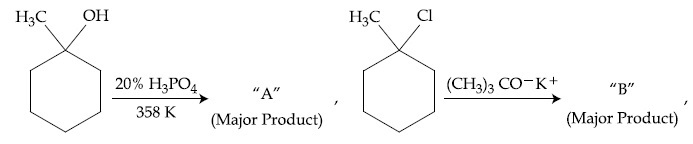
The products ''A'' and ''B'' formed in above reactions are :
14
The equivalents of ethylene diamine required to replace the neutral ligands from the coordination sphere of the trans-complex of CoCl3 . 4NH3 is _________. (Round off to the Nearest Integer).
15
Two salts A2X and MX have the same value of solubility product of 4.0 $$\times$$ 10$$-$$12. The ratio of their molar solubilities i.e. $${{S({A_2}X)} \over {S(MX)}}$$ = __________. (Round off to the Nearest Integer)
16
Complete combustion of 750 g of an organic compound provides 420 g of CO2 and 210 g of H2O. The percentage composition of carbon and hydrogen in organic compound is 15.3 and ___________ respectively. (Round off to the Nearest Integer).
17
For the reaction $$A(g) \rightleftharpoons B(g)$$ at 495 K, $$\Delta$$rG$$^\circ$$ = $$-$$9.478 kJ mol$$-$$1.
If we start the reaction in a closed container at 495 K with 22 millimoles of A, the amount of B in the equilibrium mixture is ____________ millimoles.
(Round off to the Nearest Integer). [R = 8.314 J mol$$-$$1 K$$-$$1; ln 10 = 2.303]
If we start the reaction in a closed container at 495 K with 22 millimoles of A, the amount of B in the equilibrium mixture is ____________ millimoles.
(Round off to the Nearest Integer). [R = 8.314 J mol$$-$$1 K$$-$$1; ln 10 = 2.303]
18
$$2MnO_4^ - + b{C_2}O_4^{2 - } + c{H^ + } \to xM{n^{2 + }} + yC{O_2} + z{H_2}O$$
If the above equation is balanced with integer coefficients, the value of c is ___________. (Round off to the Nearest Integer).
If the above equation is balanced with integer coefficients, the value of c is ___________. (Round off to the Nearest Integer).
19
A 6.50 molal solution of KOH (aq.) has a density of 1.89 g cm$$-$$3. The molarity of the solution is ____________ mol dm$$-$$3. (Round off to the Nearest Integer).
[Atomic masses : K : 39.0 u; O : 16.0 u; H : 1.0 u]
[Atomic masses : K : 39.0 u; O : 16.0 u; H : 1.0 u]
20
AB2 is 10% dissociated in water to A2+ and B$$-$$. The boiling point of a 10.0 molal aqueous solution of AB2 is __________$$^\circ$$C. (Round off to the Nearest Integer).
[Given : Molal elevation constant of water Kb = 0.5 K kg mol$$-$$1 boiling point of pure water = 100$$^\circ$$C]
[Given : Molal elevation constant of water Kb = 0.5 K kg mol$$-$$1 boiling point of pure water = 100$$^\circ$$C]
21
When light of wavelength 248 nm falls on a metal of threshold energy 3.0 eV, the de-Broglie wavelength of emitted electrons is _______$$\mathop A\limits^o $$. (Round off to the Nearest Integer).
[ Use : $$\sqrt 3 $$ = 1.73, h = 6.63 $$\times$$ 10$$-$$34 Js
me = 9.1 $$\times$$ 10$$-$$31 kg; c = 3.0 $$\times$$ 108 ms$$-$$1; 1eV = 1.6 $$\times$$ 10$$-$$19 J]
[ Use : $$\sqrt 3 $$ = 1.73, h = 6.63 $$\times$$ 10$$-$$34 Js
me = 9.1 $$\times$$ 10$$-$$31 kg; c = 3.0 $$\times$$ 108 ms$$-$$1; 1eV = 1.6 $$\times$$ 10$$-$$19 J]
22
The decomposition of formic acid on gold surface follows first order kinetics. If the rate constant at 300 K is 1.0 $$\times$$ 10$$-$$3 s$$-$$1 and the activation energy Ea = 11.488 kJ mol$$-$$1, the rate constant at 200 K is ____________ $$\times$$ 10$$-$$5 s$$-$$1. (Round off to the Nearest Integer). (Given : R = 8.314 J mol$$-$$1 K$$-$$1)
Mathematics
1
Let a vector $$\alpha \widehat i + \beta \widehat j$$ be obtained by rotating the vector $$\sqrt 3 \widehat i + \widehat j$$ by an angle 45$$^\circ$$ about the origin in counterclockwise direction in the first quadrant. Then the area of triangle having vertices ($$\alpha$$, $$\beta$$), (0, $$\beta$$) and (0, 0) is equal to :
2
Let $${S_k} = \sum\limits_{r = 1}^k {{{\tan }^{ - 1}}\left( {{{{6^r}} \over {{2^{2r + 1}} + {3^{2r + 1}}}}} \right)} $$. Then $$\mathop {\lim }\limits_{k \to \infty } {S_k}$$ is equal to :
3
Let the position vectors of two points P and Q be 3$$\widehat i$$ $$-$$ $$\widehat j$$ + 2$$\widehat k$$ and $$\widehat i$$ + 2$$\widehat j$$ $$-$$ 4$$\widehat k$$, respectively. Let R and S be two points such that the direction ratios of lines PR and QS are (4, $$-$$1, 2) and ($$-$$2, 1, $$-$$2), respectively. Let lines PR and QS intersect at T. If the vector $$\overrightarrow {TA} $$ is perpendicular to both $$\overrightarrow {PR} $$ and $$\overrightarrow {QS} $$ and the length of vector $$\overrightarrow {TA} $$ is $$\sqrt 5 $$ units, then the modulus of a position vector of A is :
4
The number of elements in the set {x $$\in$$ R : (|x| $$-$$ 3) |x + 4| = 6} is equal to :
5
Let a complex number z, |z| $$\ne$$ 1,
satisfy $${\log _{{1 \over {\sqrt 2 }}}}\left( {{{|z| + 11} \over {{{(|z| - 1)}^2}}}} \right) \le 2$$. Then, the largest value of |z| is equal to ____________.
satisfy $${\log _{{1 \over {\sqrt 2 }}}}\left( {{{|z| + 11} \over {{{(|z| - 1)}^2}}}} \right) \le 2$$. Then, the largest value of |z| is equal to ____________.
6
Let $$A = \left[ {\matrix{
i & { - i} \cr
{ - i} & i \cr
} } \right],i = \sqrt { - 1} $$. Then, the system of linear equations $${A^8}\left[ {\matrix{
x \cr
y \cr
} } \right] = \left[ {\matrix{
8 \cr
{64} \cr
} } \right]$$ has :
7
If n is the number of irrational terms in the
expansion of $${\left( {{3^{1/4}} + {5^{1/8}}} \right)^{60}}$$, then (n $$-$$ 1) is divisible by :
expansion of $${\left( {{3^{1/4}} + {5^{1/8}}} \right)^{60}}$$, then (n $$-$$ 1) is divisible by :
8
The locus of the midpoints of the chord of the circle, x2 + y2 = 25 which is tangent to the hyperbola, $${{{x^2}} \over 9} - {{{y^2}} \over {16}} = 1$$ is :
9
Let the functions f : R $$ \to $$ R and g : R $$ \to $$ R be defined as :
$$f(x) = \left\{ {\matrix{ {x + 2,} & {x < 0} \cr {{x^2},} & {x \ge 0} \cr } } \right.$$ and
$$g(x) = \left\{ {\matrix{ {{x^3},} & {x < 1} \cr {3x - 2,} & {x \ge 1} \cr } } \right.$$
Then, the number of points in R where (fog) (x) is NOT differentiable is equal to :
$$f(x) = \left\{ {\matrix{ {x + 2,} & {x < 0} \cr {{x^2},} & {x \ge 0} \cr } } \right.$$ and
$$g(x) = \left\{ {\matrix{ {{x^3},} & {x < 1} \cr {3x - 2,} & {x \ge 1} \cr } } \right.$$
Then, the number of points in R where (fog) (x) is NOT differentiable is equal to :
10
Consider three observations a, b, and c such that b = a + c. If the standard deviation of a + 2, b + 2, c + 2 is d, then which of the following is true?
11
The range of a$$\in$$R for which the
function f(x) = (4a $$-$$ 3)(x + loge 5) + 2(a $$-$$ 7) cot$$\left( {{x \over 2}} \right)$$ sin2$$\left( {{x \over 2}} \right)$$, x $$\ne$$ 2n$$\pi$$, n$$\in$$N has critical points, is :
function f(x) = (4a $$-$$ 3)(x + loge 5) + 2(a $$-$$ 7) cot$$\left( {{x \over 2}} \right)$$ sin2$$\left( {{x \over 2}} \right)$$, x $$\ne$$ 2n$$\pi$$, n$$\in$$N has critical points, is :
12
If for x $$\in$$ $$\left( {0,{\pi \over 2}} \right)$$, log10sinx + log10cosx = $$-$$1 and log10(sinx + cosx) = $${1 \over 2}$$(log10 n $$-$$ 1), n > 0, then the value of n is equal to :
13
A pack of cards has one card missing. Two cards are drawn randomly and are found to be spades. The probability that the missing card is not a spade, is :
14
If y = y(x) is the solution of the differential equation,
$${{dy} \over {dx}} + 2y\tan x = \sin x,y\left( {{\pi \over 3}} \right) = 0$$, then the maximum value of the function y(x) over R is equal to:
$${{dy} \over {dx}} + 2y\tan x = \sin x,y\left( {{\pi \over 3}} \right) = 0$$, then the maximum value of the function y(x) over R is equal to:
15
Let the curve y = y(x) be the solution of the differential equation, $${{dy} \over {dx}}$$ = 2(x + 1). If the numerical value of area bounded by the curve y = y(x) and x-axis is $${{4\sqrt 8 } \over 3}$$, then the value of y(1) is equal to _________.
16
Let f : R $$ \to $$ R be a continuous function such that f(x) + f(x + 1) = 2, for all x$$\in$$R.
If $${I_1} = \int\limits_0^8 {f(x)dx} $$ and $${I_2} = \int\limits_{ - 1}^3 {f(x)dx} $$, then the value of I1 + 2I2 is equal to ____________.
If $${I_1} = \int\limits_0^8 {f(x)dx} $$ and $${I_2} = \int\limits_{ - 1}^3 {f(x)dx} $$, then the value of I1 + 2I2 is equal to ____________.
17
If the normal to the curve y(x) = $$\int\limits_0^x {(2{t^2} - 15t + 10)dt} $$ at a point (a, b) is parallel to the line x + 3y = $$-$$5, a > 1, then the value of | a + 6b | is equal to ___________.
18
Consider an arithmetic series and a geometric series having four initial terms from the set {11, 8, 21, 16, 26, 32, 4}. If the last terms of these series are the maximum possible four digit numbers, then the number of common terms in these two series is equal to ___________.
19
If $$\mathop {\lim }\limits_{x \to 0} {{a{e^x} - b\cos x + c{e^{ - x}}} \over {x\sin x}} = 2$$, then a + b + c is equal to ____________.
20
Let z and $$\omega$$ be two complex numbers such that $$\omega = z\overline z - 2z + 2,\left| {{{z + i} \over {z - 3i}}} \right| = 1$$ and Re($$\omega$$) has minimum value. Then, the minimum value of n $$\in$$ N for which $$\omega$$n is real, is equal to ______________.
21
The total number of 3 $$\times$$ 3 matrices A having entries from the set {0, 1, 2, 3} such that the sum of all the diagonal entries of AAT is 9, is equal to _____________.
Physics
1
The pressure acting on a submarine is 3 $$\times$$ 105 Pa at a certain depth. If the depth is doubled, the percentage increase in the pressure acting on the submarine would be :
(Assume that atmospheric pressure is 1 $$\times$$ 105 Pa density of water is 103 kg m$$-$$3, g = 10 ms$$-$$2)
(Assume that atmospheric pressure is 1 $$\times$$ 105 Pa density of water is 103 kg m$$-$$3, g = 10 ms$$-$$2)
2
The velocity-displacement graph describing the motion of bicycle is shown in the figure.
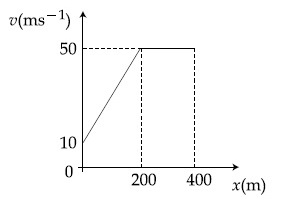
The acceleration-displacement graph of the bicycle's motion is best described by :

The acceleration-displacement graph of the bicycle's motion is best described by :
3
A block of mass m slides along a floor while a force of magnitude F is applied to it at an angle $$\theta$$ as shown in figure. The coefficient of kinetic friction is $$\mu$$k. then, the block's acceleration 'a' is given by :
(g is acceleration due to gravity)
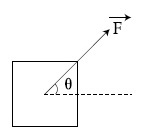
(g is acceleration due to gravity)

4
A block of 200 g mass moves with a uniform speed in a horizontal circular groove, with vertical side walls of radius 20 cm. If the block takes 40 s to complete one round, the normal force by the side walls of the groove is :
5
Time period of a simple pendulum is T inside a lift when the lift is stationary. If the lift moves upwards with an acceleration g/2, the time period of pendulum will be :
6
The angle of deviation through a prism is minimum when
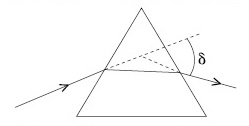
(A) Incident ray and emergent ray are symmetric to the prism.
(B) The refracted ray inside the prism becomes parallel to its base
(C) Angle of incidence is equal to that of the angle of emergence
(D) When angle of emergence is double the angle of incidence
Choose the correct answer from the options given below :

(A) Incident ray and emergent ray are symmetric to the prism.
(B) The refracted ray inside the prism becomes parallel to its base
(C) Angle of incidence is equal to that of the angle of emergence
(D) When angle of emergence is double the angle of incidence
Choose the correct answer from the options given below :
7
Four equal masses, m each are placed at the comers of a square of length (l) as shown in the figure. The moment of inertia of the system about an axis passing through A and parallel to DB would be :
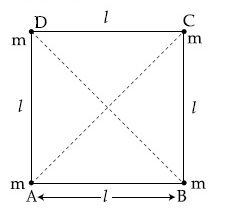

8
In thermodynamics, heat and work are :
9
For changing the capacitance of a given parallel plate capacitor, a dielectric material of dielectric constant K is used, which has the same area as the plates of the capacitor. The thickness of the dielectric slab is $${3 \over 4}$$d, where 'd' is the separation between the plates of parallel plate capacitor. The new capacitance (C') in terms of original capacitance (C0) is given by the following relation :
10
A plane electromagnetic wave of frequency 500 MHz is travelling in vacuum along y-direction. At a particular point in space and time,
$$\overrightarrow B $$ = 8.0 $$\times$$ 10$$-$$8 $$\widehat z$$T. The value of electric field at this point is :
(speed of light = 3 $$\times$$ 108 ms$$-$$1)
$$\widehat x$$, $$\widehat y$$, $$\widehat z$$ are unit vectors along x, y and z directions.
$$\overrightarrow B $$ = 8.0 $$\times$$ 10$$-$$8 $$\widehat z$$T. The value of electric field at this point is :
(speed of light = 3 $$\times$$ 108 ms$$-$$1)
$$\widehat x$$, $$\widehat y$$, $$\widehat z$$ are unit vectors along x, y and z directions.
11
The maximum and minimum distances of a comet from the Sun are 1.6 $$\times$$ 1012 m and 8.0 $$\times$$ 1010 m respectively. If the speed of the comet at the nearest point is 6 $$\times$$ 104 ms$$-$$1, the speed at the farthest point is :
12
A conducting wire of length 'l', area of cross-section A and electric resistivity $$\rho$$ is connected between the terminals of a battery. A potential difference V is developed between its ends, causing an electric current.
If the length of the wire of the same material is doubled and the area of cross-section is halved, the resultant current would be :
If the length of the wire of the same material is doubled and the area of cross-section is halved, the resultant current would be :
13
For an electromagnetic wave travelling in free space, the relation between average energy densities due to electric (Ue) and magnetic (Um) fields is :
14
The stopping potential in the context of photoelectric effect depends on the following property of incident electromagnetic radiation :
15
An RC circuit as shown in the figure is driven by a AC source generating a square wave. The output wave pattern monitored by CRO would look close to :
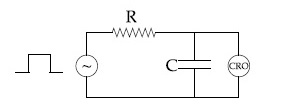

16
One main scale division of a vernier callipers is 'a' cm and nth division of the vernier scale coincide with (n $$-$$ 1)th division of the main scale. The least count of the callipers in mm is :
17
A conducting bar of length L is free to slide on two parallel conducting rails as shown in the figure
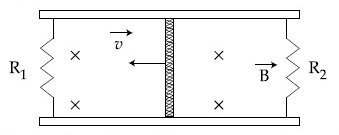
Two resistors R1 and R2 are connected across the ends of the rails. There is a uniform magnetic field $$\overrightarrow B $$ pointing into the page. An external agent pulls the bar to the left at a constant speed v.
The correct statement about the directions of induced currents I1 and I2 flowing through R1 and R2 respectively is :

Two resistors R1 and R2 are connected across the ends of the rails. There is a uniform magnetic field $$\overrightarrow B $$ pointing into the page. An external agent pulls the bar to the left at a constant speed v.
The correct statement about the directions of induced currents I1 and I2 flowing through R1 and R2 respectively is :
18
The volume V of an enclosure contains a mixture of three gases, 16 g of oxygen, 28 g of nitrogen and 44 g of carbon dioxide at absolute temperature T. Consider R as universal gas constant. The pressure of the mixture of gases is :
19
The value of power dissipated across the zener diode (Vz = 15V) connected in the circuit as shown in the figure is x $$\times$$ 10$$-$$1 watt.

The value of x, to the nearest integer, is __________.

The value of x, to the nearest integer, is __________.
20
A fringe width of 6 mm was produced for two slits separated by 1 mm apart. The screen is placed 10 m away. The wavelength of light used is 'x' nm. The value of 'x' to the nearest integer is ____________.
21
In the figure given, the electric current flowing through the 5 k$$\Omega$$ resistor is 'x' mA.
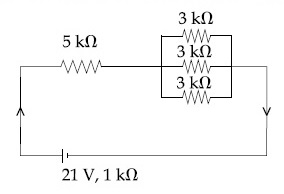
The value of x to the nearest integer is ____________.

The value of x to the nearest integer is ____________.
22
Consider a 20 kg uniform circular disk of radius 0.2 m. It is pin supported at its center and is at rest initially. The disk is acted upon by a constant force F = 20 N through a massless string wrapped around is periphery as shown in the figure.
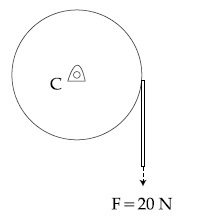
Suppose the disk makes n number of revolutions to attain an angular speed of 50 rad s$$-$$1.
The value of n, to the nearest integer, is __________.
[Given : In one complete revolution, the disk rotates by 6.28 rad]

Suppose the disk makes n number of revolutions to attain an angular speed of 50 rad s$$-$$1.
The value of n, to the nearest integer, is __________.
[Given : In one complete revolution, the disk rotates by 6.28 rad]
23
The resistance R = $${V \over I}$$, where V = (50 $$\pm$$ 2)V and I = (20 $$\pm$$ 0.2)A. The percentage error in R is 'x'%. The value of 'x' to the nearest integer is _________.
24
A sinusoidal voltage of peak value 250 V is applied to a series LCR circuit, in which R = 8$$\Omega$$, L = 24 mH and C = 60 $$\mu$$F. The value of power dissipated at resonant condition is 'x' kW. The value of x to the nearest integer is ____________.
25
In the logic circuit shown in the figure, if input A and B are 0 to 1 respectively, the output at Y would be 'x'.
The value of x is ____________.

The value of x is ____________.

26
A ball of mass 10 kg moving with a velocity $$10\sqrt 3 $$ m s$$-$$1 along X-axis, hits another ball of mass 20 kg which is at rest. After collision, the first ball comes to rest and the second one disintegrates into two equal pieces. One of the pieces starts moving along Y-axis at a speed of 10 m/s. The second piece starts moving at a speed of 20 m/s at an angle $$\theta$$ (degree) with respect to the X-axis.
The configuration of pieces after collision is shown in the figure.
The value of $$\theta$$ to the nearest integer is ____________.

The configuration of pieces after collision is shown in the figure.
The value of $$\theta$$ to the nearest integer is ____________.

27
The first three spectral lines of H-atom in the Balmer series are
given $$\lambda$$1, $$\lambda$$2, $$\lambda$$3 considering the Bohr atomic model, the wave lengths of first and third spectral lines $$\left( \frac{\lambda_{1} }{\lambda_{3} } \right) $$ are related by a factor of approximately 'x' $$\times$$ 10$$-$$1.
The value of x, to the nearest integer, is _________.
given $$\lambda$$1, $$\lambda$$2, $$\lambda$$3 considering the Bohr atomic model, the wave lengths of first and third spectral lines $$\left( \frac{\lambda_{1} }{\lambda_{3} } \right) $$ are related by a factor of approximately 'x' $$\times$$ 10$$-$$1.
The value of x, to the nearest integer, is _________.
28
Consider a frame that is made up of two thin massless rods AB and AC as shown in the figure. A vertical force $$\overrightarrow P $$ of magnitude 100 N is applied at point A of the frame.

Suppose the force is $$\overrightarrow P $$ resolved parallel to the arms AB and AC of the frame.
The magnitude of the resolved component along the arm AC is xN.
The value of x, to the nearest integer, is ___________.
[Given : sin(35$$^\circ$$) = 0.573, cos(35$$^\circ$$) = 0.819
sin(110$$^\circ$$) = 0.939, cos(110$$^\circ$$) = $$-$$ 0.342 J

Suppose the force is $$\overrightarrow P $$ resolved parallel to the arms AB and AC of the frame.
The magnitude of the resolved component along the arm AC is xN.
The value of x, to the nearest integer, is ___________.
[Given : sin(35$$^\circ$$) = 0.573, cos(35$$^\circ$$) = 0.819
sin(110$$^\circ$$) = 0.939, cos(110$$^\circ$$) = $$-$$ 0.342 J