JEE Main 2020 (Online) 4th September Evening Slot
Paper was held on
Fri, Sep 4, 2020 9:30 AM
Chemistry
1
In the following reaction sequence, [C] is :


2
The Crystal Field Stabilization Energy
(CFSE) of [CoF3(H2O)3] ($$\Delta $$0 < P) is :
(CFSE) of [CoF3(H2O)3] ($$\Delta $$0 < P) is :
3
The process that is NOT endothermic in nature
is :
4
The incorrect statement(s) among (a) - (c) is
(are)
(a) W(VI) is more stable than Cr(VI).
(b) In the presence of HCl, permanganate titrations provide satisfactory results.
(c) Some lanthanoid oxides can be used as phosphors.
(a) W(VI) is more stable than Cr(VI).
(b) In the presence of HCl, permanganate titrations provide satisfactory results.
(c) Some lanthanoid oxides can be used as phosphors.
5
Among the following compounds, which one
has the shortest C – Cl bond?
6
The one that can exhibit highest paramagnetic
behaviour among the following is :
gly = glycinato; bpy = 2, 2'-bipyridine
gly = glycinato; bpy = 2, 2'-bipyridine
7
A 100 mL solution was made by adding 1.43 g
of Na2CO3.xH2O. The normality of the solution
is 0.1 N. The value of x is _____.
(The atomic mass of Na is 23 g/mol)
(The atomic mass of Na is 23 g/mol)
8
The osmotic pressure of a solution of NaCl is
0.10 atm and that of a glucose solution is
0.20 atm. The osmotic pressure of a solution
formed by mixing 1 L of the sodium chloride
solution with 2 L of
the glucose solution is x $$ \times $$ 10–3 atm. x is _____. (nearest integer)
the glucose solution is x $$ \times $$ 10–3 atm. x is _____. (nearest integer)
9
The number of molecules with energy greater
than the threshold energy for a reaction
increases five fold by a rise of temperature
from 27oC to 42oC. Its energy of activation in
J/mol is _____.
(Take ln 5 = 1.6094; R = 8.314 J mol–1 K–1)
(Take ln 5 = 1.6094; R = 8.314 J mol–1 K–1)
10
The number of chiral centres present in
threonine is ________.
11
Consider the following equations :
2Fe2+ + H2O2 $$ \to $$ xA + yB
(in basic medium)
2MnO4- + 6H+ + 5H2O2 $$ \to $$ x'C + y'D + z'E
(in acidic medium)
The sum of the stoichiometric coefficients x, y, x', y', and z' for products A, B, C, D and E, respectively, is ______.
2Fe2+ + H2O2 $$ \to $$ xA + yB
(in basic medium)
2MnO4- + 6H+ + 5H2O2 $$ \to $$ x'C + y'D + z'E
(in acidic medium)
The sum of the stoichiometric coefficients x, y, x', y', and z' for products A, B, C, D and E, respectively, is ______.
12
Which of the following compounds will form the
precipitate with aq. AgNO3 solution most
readily?
13
The major product [R] in the following
sequence of reactions as :


14
The molecule in which hybrid MOs involve only
one d-orbital of the central atom is :
15
The major product [C] of the following reaction
sequence will be :


16
250 mL of a waste solution obtained from the
workshop of a goldsmith contains 0.1 M AgNO3
and 0.1 M AuCl. The solution was electrolyzed
at 2V by passing a current of 1A for 15
minutes. The metal/metals electrodeposited will
be
[ $$E_{A{g^ + }/Ag}^0$$ = 0.80 V, $$E_{A{u^ + }/Au}^0$$ = 1.69 V ]
[ $$E_{A{g^ + }/Ag}^0$$ = 0.80 V, $$E_{A{u^ + }/Au}^0$$ = 1.69 V ]
17
The shortest wavelength of H atom in the
Lyman series is $$\lambda $$1. The longest wavelength in
the Balmar series of He+ is :
18
Five moles of an ideal gas at 1 bar and 298 K
is expanded into vacuum to double the volume.
The work done is :
19
The major product [B] in the following
reactions is :


20
If the equilibrium constant for
A ⇌ B + C is $$K_{eq}^{(1)}$$ and that of
B + C ⇌ P is $$K_{eq}^{(2)}$$, the equilibrium
constant for A ⇌ P is :
A ⇌ B + C is $$K_{eq}^{(1)}$$ and that of
B + C ⇌ P is $$K_{eq}^{(2)}$$, the equilibrium
constant for A ⇌ P is :
21
The reaction in which the hybridisation of the
underlined atom is affected is :
Mathematics
1
A test consists of 6 multiple choice questions, each having 4 alternative answers of which only one is correct. The number of ways, in which a candidate answers all six questions such that exactly four of the answers are correct, is __________.
2
If the variance of the following frequency
distribution :
Class : 10–20 20–30 30–40
Frequency : 2 x 2
is 50, then x is equal to____
Class : 10–20 20–30 30–40
Frequency : 2 x 2
is 50, then x is equal to____
3
The area (in sq. units) of the largest rectangle ABCD whose vertices A and B lie on the x-axis and vertices C and D lie on the parabola, y = x2–1 below the x-axis, is :
4
In a game two players A and B take turns in throwing a pair of fair dice starting with player A and total of scores on the two dice, in each throw is noted. A wins the game if he throws total a of 6 before B throws a total of 7 and B wins the game if he throws a total of 7 before A throws a total of six. The game stops as soon as either of the players wins. The probability of A winning the game is :
5
If the system of equations
x+y+z=2
2x+4y–z=6
3x+2y+$$\lambda $$z=$$\mu $$
has infinitely many solutions, then
x+y+z=2
2x+4y–z=6
3x+2y+$$\lambda $$z=$$\mu $$
has infinitely many solutions, then
6
The integral
$$\int\limits_{{\pi \over 6}}^{{\pi \over 3}} {{{\tan }^3}x.{{\sin }^2}3x\left( {2{{\sec }^2}x.{{\sin }^2}3x + 3\tan x.\sin 6x} \right)dx} $$
is equal to:
$$\int\limits_{{\pi \over 6}}^{{\pi \over 3}} {{{\tan }^3}x.{{\sin }^2}3x\left( {2{{\sec }^2}x.{{\sin }^2}3x + 3\tan x.\sin 6x} \right)dx} $$
is equal to:
7
Let $$f:\left( {0,\infty } \right) \to \left( {0,\infty } \right)$$ be a differentiable function such that f(1) = e and
$$\mathop {\lim }\limits_{t \to x} {{{t^2}{f^2}(x) - {x^2}{f^2}(t)} \over {t - x}} = 0$$. If f(x) = 1, then x is equal to :
$$\mathop {\lim }\limits_{t \to x} {{{t^2}{f^2}(x) - {x^2}{f^2}(t)} \over {t - x}} = 0$$. If f(x) = 1, then x is equal to :
8
The minimum value of 2sinx + 2cosx is :
9
If the perpendicular bisector of the line segment joining the points P(1 ,4) and Q(k, 3) has y-intercept equal to –4, then a value of k is :
10
Suppose the vectors x1, x2 and x3 are the
solutions of the system of linear equations,
Ax = b when the vector b on the right side is equal to b1, b2 and b3 respectively. if
$${x_1} = \left[ {\matrix{ 1 \cr 1 \cr 1 \cr } } \right]$$, $${x_2} = \left[ {\matrix{ 0 \cr 2 \cr 1 \cr } } \right]$$, $${x_3} = \left[ {\matrix{ 0 \cr 0 \cr 1 \cr } } \right]$$
$${b_1} = \left[ {\matrix{ 1 \cr 0 \cr 0 \cr } } \right]$$, $${b_2} = \left[ {\matrix{ 0 \cr 2 \cr 0 \cr } } \right]$$ and $${b_3} = \left[ {\matrix{ 0 \cr 0 \cr 2 \cr } } \right]$$,
then the determinant of A is equal to :
solutions of the system of linear equations,
Ax = b when the vector b on the right side is equal to b1, b2 and b3 respectively. if
$${x_1} = \left[ {\matrix{ 1 \cr 1 \cr 1 \cr } } \right]$$, $${x_2} = \left[ {\matrix{ 0 \cr 2 \cr 1 \cr } } \right]$$, $${x_3} = \left[ {\matrix{ 0 \cr 0 \cr 1 \cr } } \right]$$
$${b_1} = \left[ {\matrix{ 1 \cr 0 \cr 0 \cr } } \right]$$, $${b_2} = \left[ {\matrix{ 0 \cr 2 \cr 0 \cr } } \right]$$ and $${b_3} = \left[ {\matrix{ 0 \cr 0 \cr 2 \cr } } \right]$$,
then the determinant of A is equal to :
11
If $$\overrightarrow a = 2\widehat i + \widehat j + 2\widehat k$$, then the value of
$${\left| {\widehat i \times \left( {\overrightarrow a \times \widehat i} \right)} \right|^2} + {\left| {\widehat j \times \left( {\overrightarrow a \times \widehat j} \right)} \right|^2} + {\left| {\widehat k \times \left( {\overrightarrow a \times \widehat k} \right)} \right|^2}$$ is equal to____
$${\left| {\widehat i \times \left( {\overrightarrow a \times \widehat i} \right)} \right|^2} + {\left| {\widehat j \times \left( {\overrightarrow a \times \widehat j} \right)} \right|^2} + {\left| {\widehat k \times \left( {\overrightarrow a \times \widehat k} \right)} \right|^2}$$ is equal to____
12
Let PQ be a diameter of the circle x2 + y2 = 9. If $$\alpha $$ and $$\beta $$ are the lengths of the perpendiculars from P and Q on the straight line,
x + y = 2 respectively, then the maximum value of $$\alpha\beta $$ is _____.
x + y = 2 respectively, then the maximum value of $$\alpha\beta $$ is _____.
13
Let {x} and [x] denote the fractional part of x and
the greatest integer $$ \le $$ x respectively of a real
number x. If $$\int_0^n {\left\{ x \right\}dx} ,\int_0^n {\left[ x \right]dx} $$ and 10(n2 – n),
$$\left( {n \in N,n > 1} \right)$$ are three consecutive terms of a G.P., then n is equal to_____.
the greatest integer $$ \le $$ x respectively of a real
number x. If $$\int_0^n {\left\{ x \right\}dx} ,\int_0^n {\left[ x \right]dx} $$ and 10(n2 – n),
$$\left( {n \in N,n > 1} \right)$$ are three consecutive terms of a G.P., then n is equal to_____.
14
Let a1, a2, ..., an be a given A.P. whose
common difference is an integer and
Sn = a1 + a2 + .... + an. If a1 = 1, an = 300 and 15 $$ \le $$ n $$ \le $$ 50, then
the ordered pair (Sn-4, an–4) is equal to:
common difference is an integer and
Sn = a1 + a2 + .... + an. If a1 = 1, an = 300 and 15 $$ \le $$ n $$ \le $$ 50, then
the ordered pair (Sn-4, an–4) is equal to:
15
If a and b are real numbers such that
$${\left( {2 + \alpha } \right)^4} = a + b\alpha $$
where $$\alpha = {{ - 1 + i\sqrt 3 } \over 2}$$ then a + b is equal to :
$${\left( {2 + \alpha } \right)^4} = a + b\alpha $$
where $$\alpha = {{ - 1 + i\sqrt 3 } \over 2}$$ then a + b is equal to :
16
Let $$\mathop \cup \limits_{i = 1}^{50} {X_i} = \mathop \cup \limits_{i = 1}^n {Y_i} = T$$ where each Xi contains 10 elements and each Yi contains 5 elements. If each element of the set T is an element of exactly 20 of sets Xi’s and exactly 6 of sets Yi’s, then n is equal to :
17
Let $$\lambda \ne 0$$ be in R. If $$\alpha $$ and $$\beta $$ are the roots of the
equation, x2 - x + 2$$\lambda $$ = 0 and $$\alpha $$ and $$\gamma $$ are the roots of
the equation, $$3{x^2} - 10x + 27\lambda = 0$$, then $${{\beta \gamma } \over \lambda }$$ is equal to:
equation, x2 - x + 2$$\lambda $$ = 0 and $$\alpha $$ and $$\gamma $$ are the roots of
the equation, $$3{x^2} - 10x + 27\lambda = 0$$, then $${{\beta \gamma } \over \lambda }$$ is equal to:
18
The solution of the differential equation
$${{dy} \over {dx}} - {{y + 3x} \over {{{\log }_e}\left( {y + 3x} \right)}} + 3 = 0$$ is:
(where c is a constant of integration)
$${{dy} \over {dx}} - {{y + 3x} \over {{{\log }_e}\left( {y + 3x} \right)}} + 3 = 0$$ is:
(where c is a constant of integration)
19
The function
$$f(x) = \left\{ {\matrix{ {{\pi \over 4} + {{\tan }^{ - 1}}x,} & {\left| x \right| \le 1} \cr {{1 \over 2}\left( {\left| x \right| - 1} \right),} & {\left| x \right| > 1} \cr } } \right.$$ is :
$$f(x) = \left\{ {\matrix{ {{\pi \over 4} + {{\tan }^{ - 1}}x,} & {\left| x \right| \le 1} \cr {{1 \over 2}\left( {\left| x \right| - 1} \right),} & {\left| x \right| > 1} \cr } } \right.$$ is :
Physics
1
The distance between an object and a screen is 100 cm. A lens can produce real image of the
object on the screen for two different positions between the screen and the object. The distance
between these two positions is 40 cm. If the power of the lens is close to $$\left( {{N \over {100}}} \right)D$$ where N is an
integer, the value of N is _________.
2
Orange light of wavelength 6000 $$ \times $$ 10–10 m illuminates a single
slit of width 0.6 $$ \times $$ 10–4 m. The maximum possible number of diffraction minima produced on both sides of the central maximum is ___________.
slit of width 0.6 $$ \times $$ 10–4 m. The maximum possible number of diffraction minima produced on both sides of the central maximum is ___________.
3
The change in the magnitude of the volume of an ideal gas when a small additional pressure $$\Delta $$P is
applied at a constant temperature, is the same as the change when the temperature is reduced by
a small quantity $$\Delta $$T at constant pressure. The initial temperature and pressure of the gas were 300
K and 2 atm. respectively.
If |$$\Delta $$T| = C|$$\Delta $$P| then value of C in (K/atm.) is _________.
If |$$\Delta $$T| = C|$$\Delta $$P| then value of C in (K/atm.) is _________.
4
In a photoelectric effect experiment, the graph of stopping potential V versus reciprocal of wavelength
obtained is shown in the figure. As the intensity of incident radiation is increased :


5
Identify the operation performed by the circuit given below :


6
Four resistances 40 $$\Omega $$, 60 $$\Omega $$, 90 $$\Omega $$ and 110 $$\Omega $$ make the arms of a quadrilateral ABCD. Across AC is
a battery of emf 40 V and internal resistance negligible.The potential difference across BD in V is
_______.


7
A quantity x is given by $$\left( {{{IF{v^2}} \over {W{L^4}}}} \right)$$ in terms of moment of inertia I, force F, velocity v, work W and
Length L. The dimensional formula for x is same as that of :
8
The speed verses time graph for a particle is shown in the figure. The distance travelled (in m) by
the particle during the time interval t = 0 to t = 5 s will be________.


9
The value of current i1
flowing from A to C in the circuit diagram is :


10
For a uniform rectangular sheet shown in the figure, the ratio of moments of inertia about the axes
perpendicular to the sheet and passing through O (the centre of mass) and O' (corner point) is :
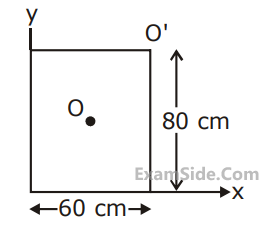

11
Two identical cylindrical vessels are kept on the ground and each contain the same liquid of density
d. The area of the base of both vessels is S but the height of liquid in one vessel is x1
and in the
other, x2
. When both cylinders are connected through a pipe of negligible volume very close to the
bottom, the liquid flows from one vessel to the other until it comes to equilibrium at a new height.
The change in energy of the system in the process is:
12
The electric field of a plane electromagnetic wave is given by
$$\overrightarrow E = {E_0}\left( {\widehat x + \widehat y} \right)\sin \left( {kz - \omega t} \right)$$
Its magnetic field will be given by :
$$\overrightarrow E = {E_0}\left( {\widehat x + \widehat y} \right)\sin \left( {kz - \omega t} \right)$$
Its magnetic field will be given by :
13
A series L-R circuit is connected to a battery of emf V. If the circuit is switched on at t = 0, then
the time at which the energy stored in the inductor reaches $$\left( {{1 \over n}} \right)$$ times of its maximum value, is :
14
Consider two uniform discs of the same thickness and different radii R1
= R and
R2 = $$\alpha $$R made of the same material. If the ratio of their moments of inertia I1 and I2 , respectively, about their axes is I1 : I2 = 1 : 16 then the value of $$\alpha $$ is :
R2 = $$\alpha $$R made of the same material. If the ratio of their moments of inertia I1 and I2 , respectively, about their axes is I1 : I2 = 1 : 16 then the value of $$\alpha $$ is :
15
Match the thermodynamic processes taking place in a system with the correct conditions. In the
table : $$\Delta $$Q is the heat supplied, $$\Delta $$W is the work done and $$\Delta $$U is change in internal energy of the
system.
| Process | Condition |
|---|---|
| (I) Adiabatic | (1) $$\Delta $$W = 0 |
| (II) Isothermal | (2) $$\Delta $$Q = 0 |
| (III) Isochoric | (3) $$\Delta $$U $$ \ne $$ 0, $$\Delta $$W $$ \ne $$ 0, $$\Delta $$Q $$ \ne $$ 0 |
| (IV) Isobaric | (4) $$\Delta $$U = 0 |
16
A small ball of mass m is thrown upward with velocity u from the ground. The ball experiences a
resistive force mkv2
where v is its speed. The maximum height attained by the ball is :
17
A cube of metal is subjected to a hydrostatic pressure of 4 GPa. The percentage change in the
length of the side of the cube is close to :
(Given bulk modulus of metal, B = 8 $$ \times $$ 1010 Pa)
(Given bulk modulus of metal, B = 8 $$ \times $$ 1010 Pa)
18
A person pushes a box on a rough horizontal plateform surface. He applies a force of 200 N over a
distance of 15 m. Thereafter, he gets progressively tired and his applied force reduces linearly with
distance to 100 N. The total distance through which the box has been moved is 30 m. What is the
work done by the person during the total movement of the box?
19
A circular coil has moment of inertia 0.8 kg m2
around any diameter and is carrying current to
produce a magnetic moment of 20 Am2
. The coil is kept initially in a vertical position and it can
rotate freely around a horizontal diameter. When a uniform magnetic field of 4 T is applied along the
vertical,it starts rotating around its horizontal diameter. The angular speed the coil acquires after
rotating by 60o will be:
20
Find the Binding energy per neucleon for $${}_{50}^{120}Sn$$. Mass of proton mp
= 1.00783 U, mass of neutron
mn
= 1.00867 U and mass of tin nucleus mSn = 119.902199 U. (take 1U = 931 MeV)
21
A capacitor C is fully charged with voltage V0. After disconnecting the voltage source, it is connected
in parallel with another uncharged capacitor of capacitance $${C \over 2}$$. The energy loss in the process
after the charge is distributed between the two capacitors is :
22
A particle of charge q and mass m is subjected to an electric field
E = E0 (1 – $$a$$x2) in the x-direction, where $$a$$ and E0 are constants. Initially the particle was at rest at x = 0. Other than the initial position the kinetic energy of the particle becomes zero when the distance of the particle from the origin is :
E = E0 (1 – $$a$$x2) in the x-direction, where $$a$$ and E0 are constants. Initially the particle was at rest at x = 0. Other than the initial position the kinetic energy of the particle becomes zero when the distance of the particle from the origin is :
23
A body is moving in a low circular orbit about a planet of mass M and radius R. The radius of the
orbit can be taken to be R itself. Then the ratio of the speed of this body in the orbit to the escape
velocity from the planet is:
24
A paramagnetic sample shows a net magnetisation of 6 A/m when it is placed in an external
magnetic field of 0.4 T at a temperature of 4 K. When the sample is placed in an external magnetic
field of 0.3 T at a temperature of 24 K, then the magnetisation will be: