JEE Main 2021 (Online) 17th March Evening Shift
Paper was held on
Wed, Mar 17, 2021 9:30 AM
Chemistry
1
$${C_{12}}{H_{22}}{O_{11}} + {H_2}O\buildrel {Enzyme\,A} \over
\longrightarrow \mathop {{C_6}{H_{12}}{O_6}}\limits_{Glu\cos e} + \mathop {{C_6}{H_{12}}{O_6}}\limits_{Fructose} $$
$$\mathop {{C_6}{H_{12}}{O_6}}\limits_{Glu\cos e} \buildrel {Enzyme\,B} \over \longrightarrow 2{C_2}{H_5}OH + 2C{O_2}$$
In the above reactions, the enzyme A and enzyme B respectively are :
$$\mathop {{C_6}{H_{12}}{O_6}}\limits_{Glu\cos e} \buildrel {Enzyme\,B} \over \longrightarrow 2{C_2}{H_5}OH + 2C{O_2}$$
In the above reactions, the enzyme A and enzyme B respectively are :
2
Choose the correct statement regarding the formation of carbocations A and B given.
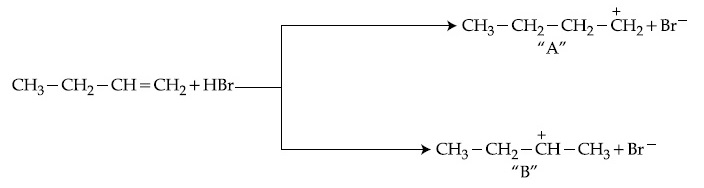

3
Nitrogen can be estimated by Kjeldahl's method for which of the following compound?
4
Amongst the following, the linear species is :
5
The correct pair(s) of the ambident nucleophiles is(are)
(A) AgCN/KCN
(B) RCOOAg/RCOOK
(C) AgNO2/KNO2
(D) AgI/KI
(A) AgCN/KCN
(B) RCOOAg/RCOOK
(C) AgNO2/KNO2
(D) AgI/KI
6
Given below are two statements :
Statement I : 2-methylbutane on oxidation with KMnO4 gives 2-methylbutan-2-ol.
Statement II : n-alkanes can be easily oxidised to corresponding alcohols with KMnO4.
Choose the correct option :
Statement I : 2-methylbutane on oxidation with KMnO4 gives 2-methylbutan-2-ol.
Statement II : n-alkanes can be easily oxidised to corresponding alcohols with KMnO4.
Choose the correct option :
7
During which of the following processes, does entropy decrease?
(A) Freezing of water to ice at 0$$^\circ$$C
(B) Freezing of water to ice at $$-$$10$$^\circ$$C
(C) N2(g) + 3H2(g) $$ \to $$ 2NH3(g)
(D) Adsorption of CO(g) on lead surface.
(E) Dissolution of NaCl in water
Choose the correct answer from the options given below :
(A) Freezing of water to ice at 0$$^\circ$$C
(B) Freezing of water to ice at $$-$$10$$^\circ$$C
(C) N2(g) + 3H2(g) $$ \to $$ 2NH3(g)
(D) Adsorption of CO(g) on lead surface.
(E) Dissolution of NaCl in water
Choose the correct answer from the options given below :
8
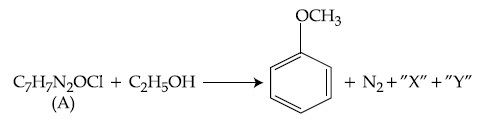
In the above reaction, the structural formula of (A), ''X'' and ''Y'' respectively are :
9
Primary, secondary and tertiary amines can be separated using:
10
Match List - I with List - II :
Choose the correct answer from the options given below :
| List - I |
List - II |
||
|---|---|---|---|
| (a) | $$[Co{(N{H_3})_6}][Cr{(CN)_6}]$$ | (i) | Linkage isomerism |
| (b) | $$[Co{(N{H_3})_3}{(N{O_2})_3}]$$ | (ii) | Solvate isomerism |
| (c) | $$[Cr{({H_2}O)_6}C{l_3}$$ | (iii) | Co-ordination isomerism |
| (d) | $$cis - {[CrC{l_2}{(ox)_2}]^{3 - }}$$ | (iv) | Optical isomerism |
Choose the correct answer from the options given below :
11
Fructose is an example of :
12
The common positive oxidation states for an element with atomic number 24, are :
13
A KCl solution of conductivity 0.14 S m$$-$$1 shows a resistance of 4.19$$\Omega$$ in a conductivity cell. If the same cell is filled with an HCl solution, the resistance drops to 1.03$$\Omega$$. The conductivity of the HCl solution is ____________ $$\times$$ 10$$-$$2 S m$$-$$1. (Round off to the Nearest Integer).
14
On complete reaction of FeCl3 with oxalic acid in aqueous solution containing KOH, resulted in the formation of product A. The secondary valency of Fe in the product A is __________. (Round off to the Nearest Integer).
15
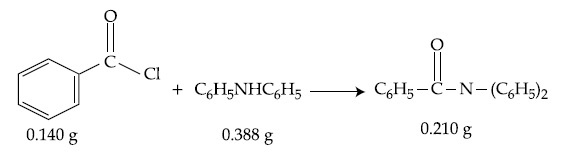
Consider the above reaction. The percentage yield of amide product is __________. (Round off to the Nearest Integer).
(Given : Atomic mass : C : 12.0 u, H : 1.0 u, N : 14.0 u, O : 16.0 u, Cl : 35.5 u)
16
The reaction 2A + B2 $$ \to $$ 2AB is an elementary reaction.
For a certain quantity of reactants, if the volume of the reaction vessel is reduced by a factor of 3, the rate of the reaction increases by a factor of ____________. (Round off to the Nearest Integer).
For a certain quantity of reactants, if the volume of the reaction vessel is reduced by a factor of 3, the rate of the reaction increases by a factor of ____________. (Round off to the Nearest Integer).
17
Consider the reaction
$$N_{2}O_{4}\left( g\right) \rightleftharpoons 2NO_{2}\left( g\right) $$
The temperature at which KC = 20.4 and KP = 600.1, is ____________ K. (Round off to the Nearest Integer). [Assume all gases are ideal and R = 0.0831 L bar K$$-$$1 mol$$-$$1]
$$N_{2}O_{4}\left( g\right) \rightleftharpoons 2NO_{2}\left( g\right) $$
The temperature at which KC = 20.4 and KP = 600.1, is ____________ K. (Round off to the Nearest Integer). [Assume all gases are ideal and R = 0.0831 L bar K$$-$$1 mol$$-$$1]
18
In the ground state of atomic Fe(Z = 26), the spin-only magnetic moment is ____________ $$\times$$ 10$$-$$1 BM. (Round off to the Nearest Integer). [Given : $$\sqrt 3 $$ = 1.73, $$\sqrt 2 $$ = 1.41 ]
19
A 1 molal K4Fe(CN)6 solution has a degree of dissociation of 0.4. Its boiling point is equal to that of another solution which contains 18.1 weight percent of a non electrolytic solute A. The molar mass of A is __________ u. (Round off to the Nearest Integer). [Density of water = 1.0 g cm$$-$$3 ]
20
The total number of C-C sigma bond/s in mesityl oxide (C6H10O) is __________. (Round off to the Nearest Integer).
Mathematics
1
If the sides AB, BC and CA of a triangle ABC have 3, 5 and 6 interior points respectively, then the total number of triangles that can be constructed using these points as vertices, is equal to :
2
Let a computer program generate only the digits 0 and 1 to form a string of binary numbers with probability of occurrence of 0 at even places be $${1 \over 2}$$ and probability of occurrence of 0 at the odd place be $${1 \over 3}$$. Then the probability that '10' is followed by '01' is equal to :
3
Let f : R $$ \to $$ R be defined as f(x) = e$$-$$xsinx. If F : [0, 1] $$ \to $$ R is a differentiable function with that F(x) = $$\int_0^x {f(t)dt} $$, then the value of $$\int_0^1 {(F'(x) + f(x)){e^x}dx} $$ lies in the interval
4
Let S1, S2 and S3 be three sets defined as
S1 = {z$$\in$$C : |z $$-$$ 1| $$ \le $$ $$\sqrt 2 $$}
S2 = {z$$\in$$C : Re((1 $$-$$ i)z) $$ \ge $$ 1}
S3 = {z$$\in$$C : Im(z) $$ \le $$ 1}
Then the set S1 $$\cap$$ S2 $$\cap$$ S3 :
S1 = {z$$\in$$C : |z $$-$$ 1| $$ \le $$ $$\sqrt 2 $$}
S2 = {z$$\in$$C : Re((1 $$-$$ i)z) $$ \ge $$ 1}
S3 = {z$$\in$$C : Im(z) $$ \le $$ 1}
Then the set S1 $$\cap$$ S2 $$\cap$$ S3 :
5
The number of solutions of the equation
$${\sin ^{ - 1}}\left[ {{x^2} + {1 \over 3}} \right] + {\cos ^{ - 1}}\left[ {{x^2} - {2 \over 3}} \right] = {x^2}$$, for x$$\in$$[$$-$$1, 1], and [x] denotes the greatest integer less than or equal to x, is :
$${\sin ^{ - 1}}\left[ {{x^2} + {1 \over 3}} \right] + {\cos ^{ - 1}}\left[ {{x^2} - {2 \over 3}} \right] = {x^2}$$, for x$$\in$$[$$-$$1, 1], and [x] denotes the greatest integer less than or equal to x, is :
6
If the curve y = y(x) is the solution of the differential equation
$$2({x^2} + {x^{5/4}})dy - y(x + {x^{1/4}})dx = {2x^{9/4}}dx$$, x > 0 which
passes through the point $$\left( {1,1 - {4 \over 3}{{\log }_e}2} \right)$$, then the value of y(16) is equal to :
$$2({x^2} + {x^{5/4}})dy - y(x + {x^{1/4}})dx = {2x^{9/4}}dx$$, x > 0 which
passes through the point $$\left( {1,1 - {4 \over 3}{{\log }_e}2} \right)$$, then the value of y(16) is equal to :
7
Let O be the origin. Let $$\overrightarrow {OP} = x\widehat i + y\widehat j - \widehat k$$ and $$\overrightarrow {OQ} = - \widehat i + 2\widehat j + 3x\widehat k$$, x, y$$\in$$R, x > 0, be such that $$\left| {\overrightarrow {PQ} } \right| = \sqrt {20} $$ and the vector $$\overrightarrow {OP} $$ is perpendicular $$\overrightarrow {OQ} $$. If $$\overrightarrow {OR} $$ = $$3\widehat i + z\widehat j - 7\widehat k$$, z$$\in$$R, is coplanar with $$\overrightarrow {OP} $$ and $$\overrightarrow {OQ} $$, then the value of x2 + y2 + z2 is equal to :
8
If the integral
$$\int_0^{10} {{{[\sin 2\pi x]} \over {{e^{x - [x]}}}}} dx = \alpha {e^{ - 1}} + \beta {e^{ - {1 \over 2}}} + \gamma $$, where $$\alpha$$, $$\beta$$, $$\gamma$$ are integers and [x] denotes the greatest integer less than or equal to x, then the value of $$\alpha$$ + $$\beta$$ + $$\gamma$$ is equal to :
$$\int_0^{10} {{{[\sin 2\pi x]} \over {{e^{x - [x]}}}}} dx = \alpha {e^{ - 1}} + \beta {e^{ - {1 \over 2}}} + \gamma $$, where $$\alpha$$, $$\beta$$, $$\gamma$$ are integers and [x] denotes the greatest integer less than or equal to x, then the value of $$\alpha$$ + $$\beta$$ + $$\gamma$$ is equal to :
9
The value of the limit
$$\mathop {\lim }\limits_{\theta \to 0} {{\tan (\pi {{\cos }^2}\theta )} \over {\sin (2\pi {{\sin }^2}\theta )}}$$ is equal to :
$$\mathop {\lim }\limits_{\theta \to 0} {{\tan (\pi {{\cos }^2}\theta )} \over {\sin (2\pi {{\sin }^2}\theta )}}$$ is equal to :
10
Consider the function f : R $$ \to $$ R defined by
$$f(x) = \left\{ \matrix{ \left( {2 - \sin \left( {{1 \over x}} \right)} \right)|x|,x \ne 0 \hfill \cr 0,\,\,x = 0 \hfill \cr} \right.$$. Then f is :
$$f(x) = \left\{ \matrix{ \left( {2 - \sin \left( {{1 \over x}} \right)} \right)|x|,x \ne 0 \hfill \cr 0,\,\,x = 0 \hfill \cr} \right.$$. Then f is :
11
The value of $$\mathop {\lim }\limits_{n \to \infty } {{[r] + [2r] + ... + [nr]} \over {{n^2}}}$$, where r is a non-zero real number and [r] denotes the greatest integer less than or equal to r, is equal to :
12
If x, y, z are in arithmetic progression with common difference d, x $$\ne$$ 3d, and the determinant of the matrix $$\left[ {\matrix{
3 & {4\sqrt 2 } & x \cr
4 & {5\sqrt 2 } & y \cr
5 & k & z \cr
} } \right]$$ is zero, then the value of k2 is :
13
Let y = y(x) be the solution of the differential equation
$$\cos x(3\sin x + \cos x + 3)dy = (1 + y\sin x(3\sin x + \cos x + 3))dx,0 \le x \le {\pi \over 2},y(0) = 0$$. Then, $$y\left( {{\pi \over 3}} \right)$$ is equal to :
$$\cos x(3\sin x + \cos x + 3)dy = (1 + y\sin x(3\sin x + \cos x + 3))dx,0 \le x \le {\pi \over 2},y(0) = 0$$. Then, $$y\left( {{\pi \over 3}} \right)$$ is equal to :
14
Let $$A = \left[ {\matrix{
a & b \cr
c & d \cr
} } \right]$$ and $$B = \left[ {\matrix{
\alpha \cr
\beta \cr
} } \right] \ne \left[ {\matrix{
0 \cr
0 \cr
} } \right]$$ such that AB = B and a + d = 2021, then the value of ad $$-$$ bc is equal to ___________.
15
Let the coefficients of third, fourth and fifth terms in the expansion of $${\left( {x + {a \over {{x^2}}}} \right)^n},x \ne 0$$, be in the ratio 12 : 8 : 3. Then the term independent of x in the expansion, is equal to ___________.
16
Let tan$$\alpha$$, tan$$\beta$$ and tan$$\gamma$$; $$\alpha$$, $$\beta$$, $$\gamma$$ $$\ne$$ $${{(2n - 1)\pi } \over 2}$$, n$$\in$$N be the slopes of three line segments OA, OB and OC, respectively, where O is origin. If circumcentre of $$\Delta$$ABC coincides with origin and its orthocentre lies on y-axis, then the value of $${\left( {{{\cos 3\alpha + \cos 3\beta + \cos 3\gamma } \over {\cos \alpha \cos \beta \cos \gamma }}} \right)^2}$$ is equal to ____________.
17
Let $$\overrightarrow x $$ be a vector in the plane containing vectors $$\overrightarrow a = 2\widehat i - \widehat j + \widehat k$$ and $$\overrightarrow b = \widehat i + 2\widehat j - \widehat k$$. If the vector $$\overrightarrow x $$ is perpendicular to $$\left( {3\widehat i + 2\widehat j - \widehat k} \right)$$ and its projection on $$\overrightarrow a $$ is $${{17\sqrt 6 } \over 2}$$, then the value of $$|\overrightarrow x {|^2}$$ is equal to __________.
18
Let $${I_n} = \int_1^e {{x^{19}}{{(\log |x|)}^n}} dx$$, where n$$\in$$N. If (20)I10 = $$\alpha$$I9 + $$\beta$$I8, for natural numbers $$\alpha$$ and $$\beta$$, then $$\alpha$$ $$-$$ $$\beta$$ equals to ___________.
19
If 1, log10(4x $$-$$ 2) and log10$$\left( {{4^x} + {{18} \over 5}} \right)$$ are in arithmetic progression for a real number x, then the value of the determinant $$\left| {\matrix{
{2\left( {x - {1 \over 2}} \right)} & {x - 1} & {{x^2}} \cr
1 & 0 & x \cr
x & 1 & 0 \cr
} } \right|$$ is equal to :
20
Consider a set of 3n numbers having variance 4. In this set, the mean of first 2n numbers is 6 and the mean of the remaining n numbers is 3. A new set is constructed by adding 1 into each of first 2n numbers, and subtracting 1 from each of the remaining n numbers. If the variance of the new set is k, then 9k is equal to __________.
21
Let f : [$$-$$1, 1] $$ \to $$ R be defined as f(x) = ax2 + bx + c for all x$$\in$$[$$-$$1, 1], where a, b, c$$\in$$R such that f($$-$$1) = 2, f'($$-$$1) = 1 for x$$\in$$($$-$$1, 1) the maximum value of f ''(x) is $${{1 \over 2}}$$. If f(x) $$ \le $$ $$\alpha$$, x$$\in$$[$$-$$1, 1], then the least value of $$\alpha$$ is equal to _________.
22
Let f : [$$-$$3, 1] $$ \to $$ R be given as
$$f(x) = \left\{ \matrix{ \min \,\{ (x + 6),{x^2}\}, - 3 \le x \le 0 \hfill \cr \max \,\{ \sqrt x ,{x^2}\} ,\,0 \le x \le 1. \hfill \cr} \right.$$
If the area bounded by y = f(x) and x-axis is A, then the value of 6A is equal to ___________.
$$f(x) = \left\{ \matrix{ \min \,\{ (x + 6),{x^2}\}, - 3 \le x \le 0 \hfill \cr \max \,\{ \sqrt x ,{x^2}\} ,\,0 \le x \le 1. \hfill \cr} \right.$$
If the area bounded by y = f(x) and x-axis is A, then the value of 6A is equal to ___________.
Physics
1
A sound wave of frequency 245 Hz travels with the speed of 300 ms$$-$$1 along the positive x-axis. Each point of the wave moves to and from through a total distance of 6 cm. What will be the mathematical expression of this travelling wave?
2
Which one of the following will be the output of the given circuit?


3
Match List - I with List - II
Choose the most appropriate answer from the options given below :
| List - I | List - II | ||
|---|---|---|---|
| (a) | Phase difference between current and voltage in a purely resistive AC circuit | (i) | $${\pi \over 2}$$; current leads voltage |
| (b) | Phase difference between current and voltage in a pure inductive AC circuit | (ii) | zero |
| (c) | Phase difference between current and voltage in a pure capacitive AC circuit | (iii) | $${\pi \over 2}$$; current lags voltage |
| (d) | Phase difference between current and voltage in an LCR series circuit | (iv) | $${\tan ^{ - 1}}\left( {{{{X_C} - {X_L}} \over R}} \right)$$ |
Choose the most appropriate answer from the options given below :
4
The atomic hydrogen emits a line spectrum consisting of various series. Which series of hydrogen atomic spectra is lying in the visible region?
5
A hairpin like shape as shown in figure is made by bending a long current carrying wire. What is the magnitude of a magnetic field at point P which lies on the centre of the semicircle?
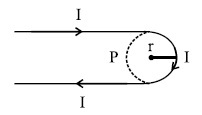

6
Two identical photocathodes receive the light of frequencies f1 and f2 respectively. If the velocities of the photo-electrons coming out are v1 and v2 respectively, then
7
If one mole of the polyatomic gas is having two vibrational modes and $$\beta$$ is the ratio of molar specific heats for polyatomic gas $$\left( {\beta = {{{C_P}} \over {{C_V}}}} \right)$$ then the value of $$\beta$$ is :
8
Two cells of emf 2E and E with internal resistance r1 and r2 respectively are connected in series to an external resistor R (see figure). The value of R, at which the potential difference across the terminals of the first cell becomes zero is


9
What happens to the inductive reactance and the current in a purely inductive circuit if the frequency is halved?
10
A sphere of mass 2 kg and radius 0.5 m is rolling with an initial speed of 1 ms-1 goes up an inclined plane which makes an angle of 30$$^\circ$$ with the horizontal plane, without slipping. How long will the sphere take to return to the starting point A?

11
Two particles A and B of equal masses are suspended from two massless springs of spring constants K1 and K2 respectively. If the maximum velocities during oscillations are equal, the ratio of the amplitude of A and B is
12
The velocity of a particle is v = v0 + gt + Ft2. Its position is x = 0 at t = 0; then its displacement after time (t = 1) is :
13
A rubber ball is released from a height of 5 m above the floor. It bounces back repeatedly, always rising to $${{81} \over {100}}$$ of the height through which it falls. Find the average speed of the ball. (Take g = 10 ms$$-$$2)
14
The four arms of a Wheatstone bridge have resistances as shown in the figure. A galvanometer of 15$$\Omega$$ resistance is connected across BD. Calculate the current through the galvanometer when a potential difference of 10V is maintained across AC.


15
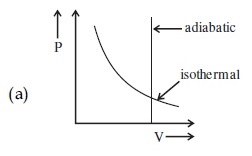
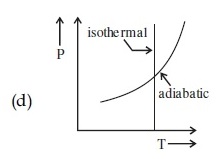
Which one is the correct option for the two different thermodynamic processes?






16
Two identical blocks A and B each of mass m resting on the smooth horizontal floor are connected by a light spring of natural length L and spring constant K. A third block C of mass m moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is


17
A geostationary satellite is orbiting around an arbitrary planet 'P' at a height of 11R above the surface of 'P', R being the radius of 'P'. The time period of another satellite in hours at a height of 2R from the surface of 'P' is _________. 'P' has the time period of 24 hours.
18
An object is located at 2 km beneath the surface of the water. If the fractional compression $${{\Delta V} \over V}$$ is 1.36%, the ratio of hydraulic stress to the corresponding hydraulic strain will be ____________. [Given : density of water is 1000 kgm$$-$$3 and g = 9.8 ms$$-$$2]
19
Suppose you have taken a dilute solution of oleic acid in such a way that its concentration becomes 0.01 cm3 of oleic acid per cm3 of the solution. Then you make a thin film of this solution (monomolecular thickness) of area 4 cm2 by considering 100 spherical drops of radius $${\left( {{3 \over {40\pi }}} \right)^{{1 \over 3}}} \times {10^{ - 3}}$$ cm. Then the thickness of oleic acid layer will be x $$\times$$ 10$$-$$14 m. Where x is ____________.
20
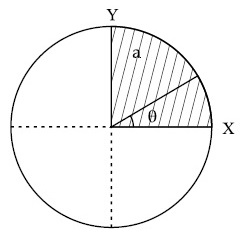
The disc of mass M with uniform surface mass density $$\sigma$$ is shown in the figure. The centre of mass of the quarter disc (the shaded area) is at the position $${x \over 3}{a \over \pi },{x \over 3}{a \over \pi }$$ where x is _____________. (Round off to the Nearest Integer).
[a is an area as shown in the figure]
[a is an area as shown in the figure]

21
The image of an object placed in air formed by a convex refracting surface is at a distance of 10 m behind the surface. The image is real and is at $${{{2^{rd}}} \over 3}$$ of the distance of the object from the surface. The wavelength of light inside the surface is $${2 \over 3}$$ times the wavelength in air. The radius of the curved surface is $${x \over {13}}$$ m. The value of 'x' is ___________.
22
The electric field intensity produced by the radiation coming from a 100 W bulb at a distance of 3 m is E. The electric field intensity produced by the radiation coming from 60W at the same distance is $$\sqrt {{x \over 5}} $$E. Where the value of x = ____________.
23
The electric field in a region is given by $$\overrightarrow E = {2 \over 5}{E_0}\widehat i + {3 \over 5}{E_0}\widehat j$$ with $${E_0} = 4.0 \times {10^3}{N \over C}$$. The flux of this field through a rectangular surface area 0.4 m2 parallel to the Y-Z plane is __________ Nm2C$$-$$1.
24
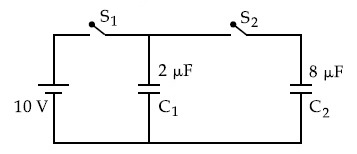
A 2$$\mu$$F capacitor C1 is first charged to a potential difference of 10V using a battery. Then the battery is removed and the capacitor is connected to an uncharged capacitor C2 of 8 $$\mu$$F. The charge in C2 on equilibrium condition is ____________ $$\mu$$C. (Round off to the Nearest Integer)

25
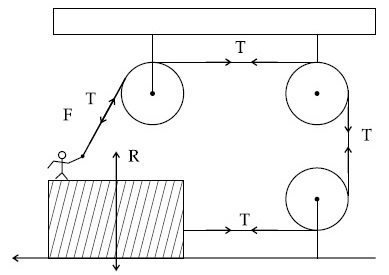
A boy of mass 4 kg is standing on a piece of wood having mass 5 kg. If the coefficient of friction between the wood and the floor is 0.5, the maximum force that the boy can exert on the rope so that the piece of wood does not move from its place is __________ N. (Round off to the Nearest Integer) [Take g = 10 ms-2 ]

26
A body of mass 1 kg rests on a horizontal floor with which it has a coefficient of static friction $${1 \over {\sqrt 3 }}$$. It is desired to make the body move by applying the minimum possible force F N. The value of F will be ____________. (Round off to the Nearest Integer) [Take g = 10 ms$$-$$2 ]
27
A particle of mass m moves in a circular orbit in a
central potential field U(r) = U0r4. If Bohr's quantization conditions
are applied, radii of possible
orbitals rn vary with $${n^{{1 \over \alpha }}}$$, where $$\alpha$$ is ____________.
central potential field U(r) = U0r4. If Bohr's quantization conditions
are applied, radii of possible
orbitals rn vary with $${n^{{1 \over \alpha }}}$$, where $$\alpha$$ is ____________.
28
Seawater at a frequency f = 9 $$\times$$ 102 Hz, has permittivity $$\varepsilon $$ = 80$$\varepsilon $$0 and resistivity $$\rho$$ = 0.25 $$\Omega$$m. Imagine a parallel plate capacitor is immersed in seawater and is driven by an alternating voltage source V(t) = V0 sin(2$$\pi$$ft). Then the conduction current density becomes 10x times the displacement current density after time t = $${1 \over {800}}$$s. The value of x is _____________. (Given : $${1 \over {4\pi {\varepsilon _0}}} = 9 \times {10^9}$$ Nm2C$$-$$2)