JEE Main 2016 (Offline)
Paper was held on
Sun, Apr 3, 2016 9:30 AM
Chemistry
1
Decomposition of H2O2 follows a first order reaction. In fifty minutes the concentration of H2O2 decreases
from 0.5 to 0.125 M in one such decomposition. When the concentration of H2O2 reaches 0.05 M, the rate of formation of O2 will be :
2
Galvanization is applying a coating of :
3
18 g glucose (C6H12O6) is added to 178.2 g water. The vapor pressure of water (in torr) for this aqueous solution is :
4
The reaction of propene with HOCl (Cl2 + H2O) proceeds through the intermediate:
5
At 300 K and 1 atm, 15 mL of a gaseous hydrocarbon requires 375 mL air containing 20% O2 by volume
for complete combustion. After combustion the gases occupy 345 mL. Assuming that the water formed is
in liquid form and the volumes were measured at the same temperature and pressure, the formula of the hydrocarbon is:
6
The distillation technique most suited for separating glycerol from spent-lye in the soap industry is :
7
The reaction of zinc with dilute and concentrated nitric acid, respectively, produces :
8
The equilibrium constant at 298 K for a reaction A + B $$\leftrightharpoons$$ C + D is 100. If the initial concentration of
all the four species were 1M each, then equilibrium concentration of D (in mol L–1) will be:
9
The heats of combustion of carbon and carbon monoxide are –393.5 and –283.5 kJ mol–1, respectively. The
heat of formation (in kJ) of carbon monoxide per mole is :
10
The product of the reaction given below is :


11
$$2$$-chloro-$$2$$-methylpentane on reaction with sodium methoxide in methanol yields:


12
The absolute configuration of

is :

is :
13
In the Hofmann bromamide degradation reaction, the number of moles of NaOH and Br2 used per mole of
amine produced are:
14
Thiol group is present in :
15
The pair having the same magnetic moment is :
[At. No.: Cr = 24, Mn = 25, Fe = 26, Co = 27]
[At. No.: Cr = 24, Mn = 25, Fe = 26, Co = 27]
16
Which one of the following complexes shows optical isomerism?
(en = ethylenediamine)
(en = ethylenediamine)
17
Which of the following compounds is metallic and ferromagnetic ?
18
A stream of electrons from a heated filament was passed between two charged plates kept at a potential
difference V esu. If e and m are charge and mass of an electron, respectively, then the value of h / $$\lambda $$ (where
$$\lambda $$ is wavelength associated with electron wave) is given by :
19
The species in which the $\mathrm{N}$ atom is in a state of $s p$ hybridization is :
Mathematics
1
For $$x \in \,R,\,\,f\left( x \right) = \left| {\log 2 - \sin x} \right|\,\,$$
and $$\,\,g\left( x \right) = f\left( {f\left( x \right)} \right),\,\,$$ then :
and $$\,\,g\left( x \right) = f\left( {f\left( x \right)} \right),\,\,$$ then :
2
Let $$p = \mathop {\lim }\limits_{x \to {0^ + }} {\left( {1 + {{\tan }^2}\sqrt x } \right)^{{1 \over {2x}}}}$$ then $$log$$ $$p$$ is equal to :
3
A value of $$\theta \,$$ for which $${{2 + 3i\sin \theta \,} \over {1 - 2i\,\,\sin \,\theta \,}}$$ is purely imaginary, is :
4
If the standard deviation of the numbers 2, 3, a and 11 is 3.5, then which of the following is true?
5
Let two fair six-faced dice $$A$$ and $$B$$ be thrown simultaneously. If $${E_1}$$ is the event that die $$A$$ shows up four, $${E_2}$$ is the event that die $$B$$ shows up two and $${E_3}$$ is the event that the sum of numbers on both dice is odd, then which of the following statements is $$NOT$$ true?
6
If a curve $$y=f(x)$$ passes through the point $$(1,-1)$$ and satisfies the differential equation, $$y(1+xy) dx=x$$ $$dy$$, then $$f\left( { - {1 \over 2}} \right)$$ is equal to :
7
The area (in sq. units) of the region $$\left\{ {\left( {x,y} \right):{y^2} \ge 2x\,\,\,and\,\,\,{x^2} + {y^2} \le 4x,x \ge 0,y \ge 0} \right\}$$ is :
8
The integral $$\int {{{2{x^{12}} + 5{x^9}} \over {{{\left( {{x^5} + {x^3} + 1} \right)}^3}}}} dx$$ is equal to :
9
The system of linear equations
$$\matrix{ {x + \lambda y - z = 0} \cr {\lambda x - y - z = 0} \cr {x + y - \lambda z = 0} \cr } $$
has a non-trivial solution for :10
If $$A = \left[ {\matrix{
{5a} & { - b} \cr
3 & 2 \cr
} } \right]$$ and $$A$$ adj $$A=A$$ $${A^T},$$ then $$5a+b$$ is equal to :
11
A wire of length $$2$$ units is cut into two parts which are bent respectively to form a square of side $$=x$$ units and a circle of radius $$=r$$ units. If the sum of the areas of the square and the circle so formed is minimum, then:
12
The eccentricity of the hyperbola whose length of the latus rectum is equal to $$8$$ and the length of its conjugate axis is equal to half of the distance between its foci, is :
13
If one of the diameters of the circle, given by the equation, $${x^2} + {y^2} - 4x + 6y - 12 = 0,$$ is a chord of a circle $$S$$, whose centre is at $$(-3, 2)$$, then the radius of $$S$$ is :
14
Two sides of a rhombus are along the lines, $$x - y + 1 = 0$$ and $$7x - y - 5 = 0$$. If its diagonals intersect at $$(-1, -2)$$, then which one of the following is a vertex of this rhombus?
15
If the $${2^{nd}},{5^{th}}\,and\,{9^{th}}$$ terms of a non-constant A.P. are in G.P., then the common ratio of this G.P. is :
16
If all the words (with or without meaning) having five letters,formed using the letters of the word SMALL and arranged as in a dictionary, then the position of the word SMALL is :
17
The sum of all real values of $$x$$ satisfying the equation $${\left( {{x^2} - 5x + 5} \right)^{{x^2} + 4x - 60}}\, = 1$$ is :
18
If $f(x)+2 f\left(\frac{1}{x}\right)=3 x, x \neq 0$, and $\mathrm{S}=\{x \in \mathbf{R}: f(x)=f(-x)\}$; then $\mathrm{S}:$
Physics
1
Identify the semiconductor devices whose characteristics are given below, in the order $$(a), (b), (c), (d)$$ :


2
If $$a, b, c, d$$ are inputs to a gate and $$x$$ is its output, then, as per the following time graph, the gate is :


3
Radiation of wavelength $$\lambda ,$$ is incident on a photocell. The fastest emitted electron has speed $$v.$$ If the wavelength is changed to $${{3\lambda } \over 4},$$ the speed of the fastest emitted electron will be:
4
An observer looks at a distant tree of height $$10$$ $$m$$ with a telescope of magnifying power of $$20.$$ To the observer the tree appears:
5
Arrange the following electromagnetic
radiations per quantum in the order of
increasing energy :
A : Blue light B : Yellow light
C : X-ray D : Radiowave.
A : Blue light B : Yellow light
C : X-ray D : Radiowave.
6
An arc lamp requires a direct current of
10 A at 80 V to function. If it is connected
to a 220 V (rms), 50 Hz AC supply, the
series inductor needed for it to work is
close to :
7
A particle of mass m is moving along the
side of a square of side ‘a’, with a uniform
speed v in the x-y plane as shown in the
figure :

Which of the following statements is false for the angular momentum $$\overrightarrow L $$ about the origin ?

Which of the following statements is false for the angular momentum $$\overrightarrow L $$ about the origin ?
8
The box of a pin hole camera, of length $$L,$$ has a hole of radius a. It is assumed that when the hole is illuminated by a parallel beam of light of wavelength $$\lambda $$ the spread of the spot (obtained on the opposite wall of the camera) is the sum of its geometrical spread and the spread due to diffraction. The spot would then have its minimum size (say $${b_{\min }}$$) when :
9
In an experiment for determination of refractive index of glass of a prism by $$i - \delta ,$$ plot it was found thata ray incident at angle $${35^ \circ }$$, suffers a deviation of $${40^ \circ }$$ and that it emerges at angle $${79^ \circ }.$$ In that case which of the following is closest to the maximum possible value of the refractive index?
10
Two identical wires $$A$$ and $$B,$$ each of length $$'l'$$, carry the same current $$I$$. Wire $$A$$ is bent into a circle of radius $$R$$ and wire $$B$$ is bent to form a square of side $$'a'$$. If $${B_A}$$ and $${B_B}$$ are the values of magnetic fields at the centres of the circle and square respectively, then the ratio $${{{B_A}} \over {{B_B}}}$$ is:
11
A galvanometer having a coil resistance of $$100\,\Omega $$ gives a full scale deflection, when a currect of $$1$$ $$mA$$ is passed through it. The value of the resistance, which can convert this galvanometer into ammeter giving a full scale deflection for a current of $$10$$ $$A,$$ is :
12
The temperature dependence of resistance of $$Cu$$ and undoped $$Si$$ in the temperature range $$300-400$$ $$K,$$ is best described by :
13
A combination of capacitors is set up as shown in the figure. The magnitude of the electric field, due to a point charge $$Q$$ (having a charge equal to the sum of the charges on the $$4$$ $$\mu \,F$$ and $$9$$ $$\mu \,F$$ capacitors), at a point distance $$30$$ $$m$$ from it, would equal :


14
The region between two concentric spheres of radii $$'a'$$ and $$'b',$$ respectively (see figure), have volume charge density $$\rho = {A \over r},$$ where $$A$$ is a constant and $$r$$ is the distance from the center. A such that the electric field in the region between the spheres will be constant, is :


15
A pipe open at both ends has a fundamental frequency $$f$$ in air. The pipe is dipped vertically in water so that half of it is in water. The fundamental frequency of the air column is now :
16
A uniform string of length $$20$$ $$m$$ is suspended from a rigid support. A short wave pulse is introduced at its lowest end. It starts moving up the string. The time taken to reach the supports is :
(take $${\,\,g = 10m{s^{ - 2}}}$$ )
(take $${\,\,g = 10m{s^{ - 2}}}$$ )
17
A particle performs simple harmonic motion with amplitude $$A.$$ Its speed is trebled at the instant that it is at a distance $${{2A} \over 3}$$ from equilibrium position. The new amplitude of the motion is:
18
$$'n'$$ moles of an ideal gas undergoes a process $$A$$ $$ \to $$ $$B$$ as shown in the figure. The maximum temperature of the gas during the process will be :
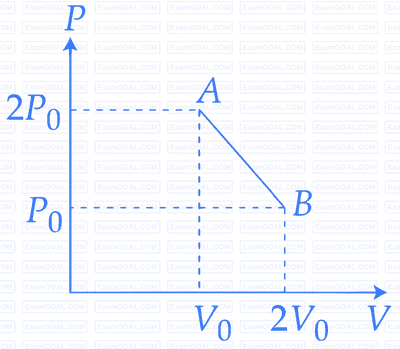

19
A roller is made by joining together two cones at their vertices $$0$$. It is kept on two rails $$AB$$ and $$CD$$, which are placed asymmetrically (see figure), with its axis perpendicular to $$CD$$ and its center $$O$$ at the center of line joining $$AB$$ and $$CD$$ (see figure). It is given a light push so that it starts rolling with its center $$O$$ moving parallel to $$CD$$ in the direction shown. As it moves, the roller will tend to :


20
An ideal gas undergoes a quasi static, reversible process in which its molar heat capacity $$C$$ remains constant. If during this process the relation of pressure $$P$$ and volume $$V$$ is given by $$P{V^n} = $$ constant, then $$n$$ is given by (Here $${C_p}$$ and $${C_v}$$ are molar specific heat at constant pressure and constant volume, respectively:
21
A pendulum clock loses $$12$$ $$s$$ a day if the temperature is $${40^ \circ }C$$ and gains $$4$$ $$s$$ a day if the temperature is $${20^ \circ }C.$$ The temperature at which the clock will show correct time, and the co-efficient of linear expansion $$\left( \alpha \right)$$ of the metal of the pendulum shaft are respectively :
22
A point particle of mass $$m,$$ moves long the uniformly rough track $$PQR$$ as shown in the figure. The coefficient of friction, between the particle and the rough track equals $$\mu .$$ The particle is released, from rest from the point $$P$$ and it comes to rest at point $$R.$$ The energies, lost by the ball, over the parts, $$PQ$$ and $$QR$$, of the track, are equal to each other , and no energy is lost when particle changes direction from $$PQ$$ to $$QR$$.

The value of the coefficient of friction $$\mu $$ and the distance $$x$$ $$(=QR),$$ are, respectively close to:

23
A satellite is revolving in a circular orbit at a height $$'h'$$ from the earth's surface (radius of earth $$R;h < < R$$). The minimum increase in its orbital velocity required, so that the satellite could escape from the earth's gravitational field, is close to : (Neglect the effect of atmosphere.)
24
A person trying to lose weight by burning fat lifts a mass of $$10$$ $$kg$$ upto a height of $$1$$ $$m$$ $$1000$$ times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up? Fat supplies $$3.8 \times {10^7}J$$ of energy per $$kg$$ which is converted to mechanical energy with a $$20\% $$ efficiency rate. Take $$g = 9.8\,m{s^{ - 2}}$$ :
25
A screw gauge with a pitch of 0.5 mm and a circular scale with 50 divisions is used to measure the
thickness of a thin sheet of Aluminium. Before starting the measurement, it is found that when the two jaws of the screw gauge are brought in contact, the 45th division coincides with the main scale line and that the zero of the main scale is barely visible. What is the thickness of the sheet if the main scale reading is 0.5 mm and the 25th division coincides with the main scale line?
26
A student measures the time period of 100 oscillations of a simple pendulum four times. The data set is 90 s, 91 s, 95 s and 92 s. If the minimum division in the measuring clock is 1 s, then the reported mean time should be :