If $$z \ne 1$$ and $$\,{{{z^2}} \over {z - 1}}\,$$ is real, then the point represented by the complex number z lies :

Let $$ABCD$$ be a parallelogram such that $$\overrightarrow {AB} = \overrightarrow q ,\overrightarrow {AD} = \overrightarrow p $$ and $$\angle BAD$$ be an acute angle. If $$\overrightarrow r $$ is the vector that coincide with the altitude directed from the vertex $$B$$ to the side $$AD,$$ then $$\overrightarrow r $$ is given by :

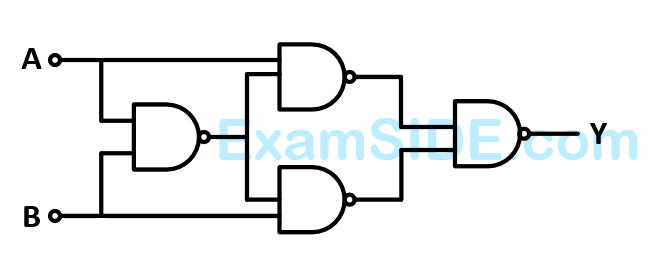
Truth table for system of four $$NAND$$ gates as shown in figure is:

A diatomic molecule is made of two masses $${m_1}$$ and $${m_2}$$ which are separated by a distance $$r.$$ If we calculate its rotational energy by applying Bohr's rule of angular momentum quantization, its energy will be given by: ($$n$$ is an integer)