The radius R of a nucleus of mass number A can be estimated by the formula
R = (1.3 $$ \times $$ 10^–15)A^1/3 m.
It follows that the mass density of a nucleus is of the order of :

(M_prot. $$ \cong $$ M_neut $$ \simeq $$ 1.67 $$ \times $$ 10^–27 kg)

A block of mass 1.9 kg is at rest at the edge of a table, of height 1 m. A bullet of mass 0.1 kg collides with the block and sticks to it. If the velocity of the bullet is 20 m/s in the horizontal direction just before the collision then the kinetic energy just before the combined system strikes the floor, is [Take g = 10 m/s² . Assume there is no rotational motion and loss of energy after the collision is negligable.]

Two resistors 400$$\Omega $$ and 800$$\Omega $$ are connected in series across a 6 V battery. The potential difference measured by a voltmeter of 10 k$$\Omega $$ across 400 $$\Omega $$ resistor is close to :

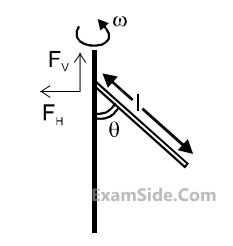
A uniform rod of length ‘$$l$$’ is pivoted at one of its ends on a vertical shaft of negligible radius. When the shaft rotates at angular speed $$\omega $$ the rod makes an angle $$\theta $$ with it (see figure). To find $$\theta $$ equate the rate of change of angular momentum (direction going into the paper) $${{m{l^2}} \over {12}}{\omega ^2}\sin \theta \cos \theta $$ about the centre of mass (CM) to the torque provided by the horizontal and vertical forces F_H and F_V about the CM. The value of $$\theta $$ is then such that :