The surface of a metal is illuminated with the light of $$400$$ $$nm.$$ The kinetic energy of the ejected photoelectrons was found to be $$1.68$$ $$eV.$$ The work function of the metal is : $$\left( {hc = 1240eV.nm} \right)$$

In an experiment, electrons are made to pass through a narrow slit of width $$'d'$$ comparable to their de Broglie wavelength. They are detected on a screen at a distance $$'D'$$ from the slit (see figure).

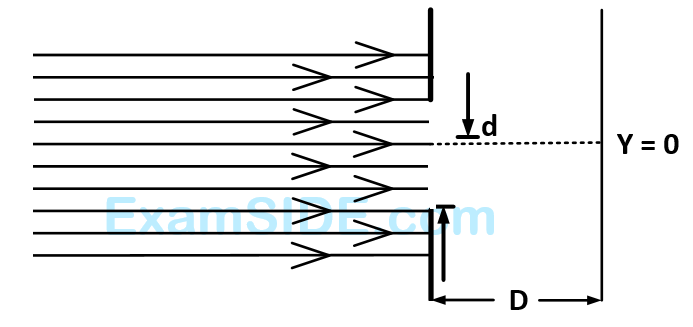
Which of the following graphs can be expected to represent the number of electrons $$'N'$$ detected as a function of the detector position $$'y'\left( {y = 0} \right.$$ corresponds to the middle of the slit$$\left. \, \right)$$

Wave property of electrons implies that they will show diffraction effects. Davisson and Germer demonstrated this by diffracting electrons from crystals. The law governing the diffraction from a crystal is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructively (see figure).

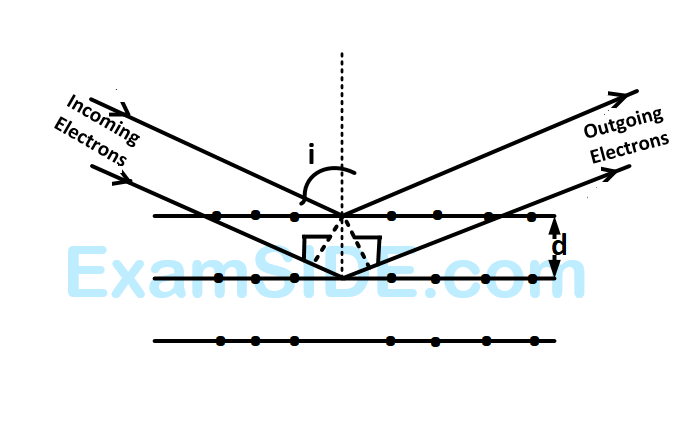
If a strong diffraction peak is observed when electrons are incident at an angle $$'i'$$ from the normal to the crystal planes with distance $$'d'$$ between them (see figure), de Broglie wavelength $${\lambda _{dB}}$$ of electrons can be calculated by the relationship ($$n$$ is an integer)

Wave property of electrons implies that they will show diffraction effects. Davisson and Germer demonstrated this by diffracting electrons from crystals. The law governing the diffraction from a crystal is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructively (see figure).

Electrons accelerated by potential $$V$$ are diffracted from a crystal. If $$d = 1\mathop A\limits^ \circ $$ and $$i = {30^ \circ },\,\,\,V$$ should be about
$$\left( {h = 6.6 \times {{10}^{ - 34}}Js,{m_e} = 9.1 \times {{10}^{ - 31}}kg,\,e = 1.6 \times {{10}^{ - 19}}C} \right)$$