Dual Nature of Radiation · Physics · JEE Main
Numerical
An electron is released from rest near an infinite non-conducting sheet of uniform charge density '$-\sigma$'. The rate of change of de-Broglie wave length associated with the electron varies inversely as nth power of time. The numerical value of n is _____.
The ratio of the power of a light source $S_1$ to that the light source $S_2$ is $2 . S_1$ is emitting $2 \times 10^{15}$ photons per second at 600 nm . If the wavelength of the source $S_2$ is 300 nm , then the number of photons per second emitted by $S_2$ is __________ $\times 10^{14}$.
In Franck-Hertz experiment, the first dip in the current-voltage graph for hydrogen is observed at $$10.2 \mathrm{~V}$$. The wavelength of light emitted by hydrogen atom when excited to the first excitation level is ________ nm. (Given hc $$=1245 \mathrm{~eV} \mathrm{~nm}, \mathrm{e}=1.6 \times 10^{-19} \mathrm{C}$$).
An atom absorbs a photon of wavelength $$500 \mathrm{~nm}$$ and emits another photon of wavelength $$600 \mathrm{~nm}$$. The net energy absorbed by the atom in this process is $$n \times 10^{-4} ~\mathrm{eV}$$. The value of n is __________. [Assume the atom to be stationary during the absorption and emission process] (Take $$\mathrm{h}=6.6 \times 10^{-34} ~\mathrm{Js}$$ and $$\mathrm{c}=3 \times 10^{8} \mathrm{~m} / \mathrm{s}$$ )
A monochromatic light is incident on a hydrogen sample in ground state. Hydrogen atoms absorb a fraction of light and subsequently emit radiation of six different wavelengths. The frequency of incident light is $$x \times 10^{15} \mathrm{~Hz}$$. The value of $$x$$ is ____________.
(Given h $$=4.25 \times 10^{-15} ~\mathrm{eVs}$$ )
The stopping potential for photoelectrons emitted from a surface illuminated by light of wavelength 6630 $$\mathop A\limits^o $$ is 0.42 V. If the threshold frequency is x $$\times$$ 1013 /s, where x is _________ (nearest integer).
(Given, speed light = 3 $$\times$$ 108 m/s, Planck's constant = 6.63 $$\times$$ 10$$-$$34 Js)
When light of frequency twice the threshold frequency is incident on the metal plate, the maximum velocity of emitted electron is v1. When the frequency of incident radiation is increased to five times the threshold value, the maximum velocity of emitted electron becomes v2. If v2 = x v1, the value of x will be __________.
Given hc = 20 $$\times$$ 10$$-$$26 J-m, mass of electron = 9 $$\times$$ 10$$-$$31 kg
(Planck constant h = 6.64 × 10–34 Js,
1 eV = 1.6 × 10–19 J, electron
mass m = 9.1 × 10–31 kg)
MCQ (Single Correct Answer)
A photoemissive substance is illuminated with a radiation of wavelength $\lambda_i$ so that it releases electrons with de-Broglie wavelength $\lambda_e$. The longest wavelength of radiation that can emit photoelectron is $\lambda_o$. Expression for de-Broglie wavelength is given by:
(m: mass of the electron, h: Planck's constant and c: speed of light)
A small mirror of mass $m$ is suspended by a massless thread of length $l$. Then the small angle through which the thread will be deflected when a short pulse of laser of energy E falls normal on the mirror
($\mathrm{c}=$ speed of light in vacuum and $g=$ acceleration due to gravity)
Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason $\mathbf{R}$
Assertion A : In photoelectric effect, on increasing the intensity of incident light the stopping potential increases.
Reason R : Increase in intensity of light increases the rate of photoelectrons emitted, provided the frequency of incident light is greater than threshold frequency.
In the light of the above statements, choose the correct answer from the options given below
An electron with mass ' m ' with an initial velocity $(\mathrm{t}=0) \overrightarrow{\mathrm{v}}=\mathrm{v}_0 \hat{i}\left(\mathrm{v}_0>0\right)$ enters a magnetic field $\overrightarrow{\mathrm{B}}=\mathrm{B}_0 \hat{j}$. If the initial de-Broglie wavelength at $\mathrm{t}=0$ is $\lambda_0$ then its value after time ' t ' would be :
A monochromatic light is incident on a metallic plate having work function $\phi$. An electron, emitted normally to the plate from a point A with maximum kinetic energy, enters a constant magnetic field, perpendicular to the initial velocity of electron. The electron passes through a curve and hits back the plate at a point $B$. The distance between $A$ and $B$ is : (Given : The magnitude of charge of an electron is e and mass is $\mathrm{m}, \mathrm{h}$ is Planck's constant and c is velocity of light. Take the magnetic field exists throughout the path of electron)
In an experiment with photoelectric effect, the stopping potential,
If $\lambda$ and $K$ are de Broglie wavelength and kinetic energy, respectively, of a particle with constant mass. The correct graphical representation for the particle will be :
Given below are two statements: one is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A) : Emission of electrons in photoelectric effect can be suppressed by applying a sufficiently negative electron potential to the photoemissive substance.
Reason (R) : A negative electric potential, which stops the emission of electrons from the surface of a photoemissive substance, varies linearly with frequency of incident radiation.
In the light of the above statements, choose the most appropriate answer from the options given below :
Which of the following phenomena cannot be explained by wave theory of light?
A proton of mass ' $m_P$ ' has same energy as that of a photon of wavelength ' $\lambda$ '. If the proton is moving at non-relativistic speed, then ratio of its de Broglie wavelength to the wavelength of photon is.
In photoelectric effect, the stopping potential $\left(\mathrm{V}_0\right) \mathrm{v} / \mathrm{s}$ frequency $(v)$ curve is plotted.
( h is the Planck's constant and $\phi_0$ is work function of metal )
(A) $\mathrm{V}_0 \mathrm{v} / \mathrm{s} v$ is linear.
(B) The slope of $\mathrm{V}_0 \mathrm{v} / \mathrm{s} v$ curve $=\frac{\phi_0}{\mathrm{~h}}$
(C) h constant is related to the slope of $\mathrm{V}_0 \mathrm{v} / \mathrm{s} v$ line.
(D) The value of electric charge of electron is not required to determine h using the $\mathrm{V}_0 \mathrm{v} / \mathrm{s} v$ curve.
(E) The work function can be estimated without knowing the value of $h$.
Choose the correct answer from the options given below :
An electron of mass ' m ' with an initial velocity $\overrightarrow{\mathrm{v}}=\mathrm{v}_0 \hat{i}\left(\mathrm{v}_0>0\right)$ enters an electric field $\overrightarrow{\mathrm{E}}=-\mathrm{E}_{\mathrm{o}} \hat{\mathrm{k}}$. If the initial de Broglie wavelength is $\lambda_0$, the value after time t would be
In photoelectric effect an em-wave is incident on a metal surface and electrons are ejected from the surface. If the work function of the metal is 2.14 eV and stopping potential is 2 V , what is the wavelength of the em-wave? (Given $\mathrm{hc}=1242 \mathrm{eVnm}$ where h is the Planck's constant and c is the speed of light in vaccum.)
A sub-atomic particle of mass $10^{-30} \mathrm{~kg}$ is moving with a velocity $2.21 \times 10^6 \mathrm{~m} / \mathrm{s}$. Under the matter wave consideration, the particle will behave closely like $\qquad$ $\left(\mathrm{h}=6.63 \times 10^{-34} \mathrm{~J} . \mathrm{s}\right)$
A light source of wavelength $\lambda$ illuminates a metal surface and electrons are ejected with maximum kinetic energy of 2 eV . If the same surface is illuminated by a light source of wavelength $\frac{\lambda}{2}$, then the maximum kinetic energy of ejected electrons will be (The work function of metal is 1 eV )
The work functions of cesium (Cs) and lithium (Li) metals are 1.9 eV and 2.5 eV , respectively. If we incident a light of wavelength 550 nm on these two metal surfaces, then photo-electric effect is possible for the case of
An electron in the ground state of the hydrogen atom has the orbital radius of $5.3 \times 10^{-11} \mathrm{~m}$ while that for the electron in third excited state is $8.48 \times 10^{-10} \mathrm{~m}$. The ratio of the de Broglie wavelengths of electron in the ground state to that in the excited state is
UV light of $$4.13 \mathrm{~eV}$$ is incident on a photosensitive metal surface having work function $$3.13 \mathrm{~eV}$$. The maximum kinetic energy of ejected photoelectrons will be:
A proton, an electron and an alpha particle have the same energies. Their de-Broglie wavelengths will be compared as :
A proton and an electron have the same de Broglie wavelength. If $$\mathrm{K}_{\mathrm{p}}$$ and $$\mathrm{K}_{\mathrm{e}}$$ be the kinetic energies of proton and electron respectively, then choose the correct relation :
A proton and an electron are associated with same de-Broglie wavelength. The ratio of their kinetic energies is:
(Assume h = 6.63 $$\times 10^{-34} \mathrm{~J} \mathrm{~s}, \mathrm{~m}_{\mathrm{e}}=9.0 \times 10^{-31} \mathrm{~kg}$$ and $$\mathrm{m}_{\mathrm{p}}=1836$$ times $$\mathrm{m}_{\mathrm{e}}$$ )
When UV light of wavelength $$300 \mathrm{~nm}$$ is incident on the metal surface having work function $$2.13 \mathrm{~eV}$$, electron emission takes place. The stopping potential is :
(Given hc $$=1240 \mathrm{~eV} \mathrm{~nm}$$ )
Which of the following phenomena does not explain by wave nature of light.
A. reflection
B. diffraction
C. photoelectric effect
D. interference
E. polarization
Choose the most appropriate answer from the options given below:
In photoelectric experiment energy of $$2.48 \mathrm{~eV}$$ irradiates a photo sensitive material. The stopping potential was measured to be $$0.5 \mathrm{~V}$$. Work function of the photo sensitive material is :
Which of the following statement is not true about stopping potential $$(\mathrm{V}_0)$$ ?
Given below are two statements :

Statement I : Figure shows the variation of stopping potential with frequency $$(v)$$ for the two photosensitive materials $$M_1$$ and $$M_2$$. The slope gives value of $$\frac{h}{e}$$, where $$h$$ is Planck's constant, e is the charge of electron.
Statement II : $$\mathrm{M}_2$$ will emit photoelectrons of greater kinetic energy for the incident radiation having same frequency.
In the light of the above statements, choose the most appropriate answer from the options given below.
Given below are two statements: one is labelled as Assertion $$\mathbf{A}$$ and the other is labelled as Reason R.
Assertion A: Number of photons increases with increase in frequency of light.
Reason R: Maximum kinetic energy of emitted electrons increases with the frequency of incident radiation.
In the light of the above statements, choose the most appropriate answer from the options given below:
Which figure shows the correct variation of applied potential difference (V) with photoelectric current (I) at two different intensities of light $$(\mathrm{I}_1<\mathrm{I}_2)$$ of same wavelengths :
How many photons per second on an average, are emitted by the source ?
(Given $\mathrm{h}=6.63 \times 10^{-34} \mathrm{Js}$ )
(Given, $\mathrm{h}=6.6 \times 10^{-34} \mathrm{Js}, \mathrm{e}=1.6 \times 10^{-19} \mathrm{C}$ )
In a photoelectric effect experiment a light of frequency 1.5 times the threshold frequency is made to fall on the surface of photosensitive material. Now if the frequency is halved and intensity is doubled, the number of photo electrons emitted will be:
When a metal surface is illuminated by light of wavelength $$\lambda$$, the stopping potential is $$8 \mathrm{~V}$$. When the same surface is illuminated by light of wavelength $$3 \lambda$$, stopping potential is $$2 \mathrm{~V}$$. The threshold wavelength for this surface is:
For the photoelectric effect, the maximum kinetic energy $$\left(E_k\right)$$ of the photoelectrons is plotted against the frequency $$(v)$$ of the incident photons as shown in figure. The slope of the graph gives

If the total energy transferred to a surface in time $$\mathrm{t}$$ is $$6.48 \times 10^5 \mathrm{~J}$$, then the magnitude of the total momentum delivered to this surface for complete absorption will be:
The work function of a substance is $$3.0 \mathrm{~eV}$$. The longest wavelength of light that can cause the emission of photoelectrons from this substance is approximately;
Two sources of light emit with a power of $$200 \mathrm{~W}$$. The ratio of number of photons of visible light emitted by each source having wavelengths $$300 \mathrm{~nm}$$ and $$500 \mathrm{~nm}$$ respectively, will be :
The de-Broglie wavelength of an electron is the same as that of a photon. If velocity of electron is $$25 \%$$ of the velocity of light, then the ratio of K.E. of electron and K.E. of photon will be:
The threshold frequency of a metal with work function $$6.63 \mathrm{~eV}$$ is :
Given below are two statements:
Statement I : Out of microwaves, infrared rays and ultraviolet rays, ultraviolet rays are the most effective for the emission of electrons from a metallic surface.
Statement II : Above the threshold frequency, the maximum kinetic energy of photoelectrons is inversely proportional to the frequency of the incident light.
In the light of above statements, choose the correct answer form the options given below
The difference between threshold wavelengths for two metal surfaces $$\mathrm{A}$$ and $$\mathrm{B}$$ having work function $$\phi_{A}=9 ~\mathrm{eV}$$ and $$\phi_{B}=4 \cdot 5 ~\mathrm{eV}$$ in $$\mathrm{nm}$$ is:
$$\{$$ Given, hc $$=1242 ~\mathrm{eV} \mathrm{nm}\}$$
A proton and an $$\alpha$$-particle are accelerated from rest by $$2 \mathrm{~V}$$ and $$4 \mathrm{~V}$$ potentials, respectively. The ratio of their de-Broglie wavelength is :
The ratio of the de-Broglie wavelengths of proton and electron having same Kinetic energy :
(Assume $$m_{p}=m_{e} \times 1849$$ )
A metallic surface is illuminated with radiation of wavelength $$\lambda$$, the stopping potential is $$V_{0}$$. If the same surface is illuminated with radiation of wavelength $$2 \lambda$$. the stopping potential becomes $$\frac{V_{o}}{4}$$. The threshold wavelength for this metallic surface will be
The variation of stopping potential $$\left(\mathrm{V}_{0}\right)$$ as a function of the frequency $$(v)$$ of the incident light for a metal is shown in figure. The work function of the surface is

The de Broglie wavelength of a molecule in a gas at room temperature (300 K) is $$\lambda_1$$. If the temperature of the gas is increased to 600 K, then the de Broglie wavelength of the same gas molecule becomes
In photo electric effect
A. The photocurrent is proportional to the intensity of the incident radiation
B. Maximum Kinetic energy with which photoelectrons are emitted depends on the intensity of incident light.
C. Max. K.E with which photoelectrons are emitted depends on the frequency of incident light.
D. The emission of photoelectrons require a minimum threshold intensity of incident radiation.
E. Max. K.E of the photoelectrons is independent of the frequency of the incident light.
Choose the correct answer from the options given below:
Proton $$(\mathrm{P})$$ and electron (e) will have same de-Broglie wavelength when the ratio of their momentum is (assume, $$\mathrm{m}_{\mathrm{p}}=1849 \mathrm{~m}_{\mathrm{e}}$$ ):
The work functions of Aluminium and Gold are $$4.1 ~\mathrm{eV}$$ and and $$5.1 ~\mathrm{eV}$$ respectively. The ratio of the slope of the stopping potential versus frequency plot for Gold to that of Aluminium is
The kinetic energy of an electron, $$\alpha$$-particle and a proton are given as $$4 \mathrm{~K}, 2 \mathrm{~K}$$ and $$\mathrm{K}$$ respectively. The de-Broglie wavelength associated with electron $$(\lambda \mathrm{e}), \alpha$$-particle $$((\lambda \alpha)$$ and the proton $$(\lambda p)$$ are as follows:
The threshold frequency of a metal is $$f_{0}$$. When the light of frequency $$2 f_{0}$$ is incident on the metal plate, the maximum velocity of photoelectrons is $$v_{1}$$. When the frequency of incident radiation is increased to $$5 \mathrm{f}_{0}$$, the maximum velocity of photoelectrons emitted is $$v_{2}$$. The ratio of $$v_{1}$$ to $$v_{2}$$ is :
A proton moving with one tenth of velocity of light has a certain de Broglie wavelength of $$\lambda$$. An alpha particle having certain kinetic energy has the same de-Brogle wavelength $$\lambda$$. The ratio of kinetic energy of proton and that of alpha particle is:
Given below are two statements : One is labelled as Assertion A and the other is labelled as Reason R
Assertion A : The beam of electrons show wave nature and exhibit interference and diffraction.
Reason R : Davisson Germer Experimentally verified the wave nature of electrons.
In the light of the above statements, choose the most appropriate answer from the options given below :
If a source of electromagnetic radiation having power $$15 \mathrm{~kW}$$ produces $$10^{16}$$ photons per second, the radiation belongs to a part of spectrum is.
(Take Planck constant $$h=6 \times 10^{-34} \mathrm{Js}$$ )
A small object at rest, absorbs a light pulse of power $$20 \mathrm{~mW}$$ and duration $$300 \mathrm{~ns}$$. Assuming speed of light as $$3 \times 10^{8} \mathrm{~m} / \mathrm{s}$$, the momentum of the object becomes equal to :
The ratio of de-Broglie wavelength of an $$\alpha$$ particle and a proton accelerated from rest by the same potential is $$\frac{1}{\sqrt m}$$, the value of m is -
The threshold wavelength for photoelectric emission from a material is 5500 $$\mathop A\limits^o $$. Photoelectrons will be emitted, when this material is illuminated with monochromatic radiation from a
A. 75 W infra-red lamp
B. 10 W infra-red lamp
C. 75 W ultra-violet lamp
D. 10 W ultra-violet lamp
Choose the correct answer from the options given below :
Given below are two statements :
Statement I : Stopping potential in photoelectric effect does not depend on the power of the light source.
Statement II : For a given metal, the maximum kinetic energy of the photoelectron depends on the wavelength of the incident light.
In the light of above statements, choose the most appropriate answer from the options given below
Electron beam used in an electron microscope, when accelerated by a voltage of 20 kV, has a de-Broglie wavelength of $$\lambda_0$$. IF the voltage is increased to 40 kV, then the de-Broglie wavelength associated with the electron beam would be :
From the photoelectric effect experiment, following observations are made. Identify which of these are correct.
A. The stopping potential depends only on the work function of the metal.
B. The saturation current increases as the intensity of incident light increases.
C. The maximum kinetic energy of a photo electron depends on the intensity of the incident light.
D. Photoelectric effect can be explained using wave theory of light.
Choose the correct answer from the options given below :
An $$\alpha$$ particle and a proton are accelerated from rest through the same potential difference. The ratio of linear momenta acquired by above two particles will be:
The kinetic energy of emitted electron is E when the light incident on the metal has wavelength $$\lambda$$. To double the kinetic energy, the incident light must have wavelength:
Two streams of photons, possessing energies equal to five and ten times the work function of metal are incident on the metal surface successively. The ratio of maximum velocities of the photoelectron emitted, in the two cases respectively, will be
The equation $$\lambda=\frac{1.227}{x} \mathrm{~nm}$$ can be used to find the de-Brogli wavelength of an electron. In this equation $$x$$ stands for :
Where
$$\mathrm{m}=$$ mass of electron
$$\mathrm{P}=$$ momentum of electron
$$\mathrm{K}=$$ Kinetic energy of electron
$$\mathrm{V}=$$ Accelerating potential in volts for electron
With reference to the observations in photo-electric effect, identify the correct statements from below :
(A) The square of maximum velocity of photoelectrons varies linearly with frequency of incident light.
(B) The value of saturation current increases on moving the source of light away from the metal surface.
(C) The maximum kinetic energy of photo-electrons decreases on decreasing the power of LED (light emitting diode) source of light.
(D) The immediate emission of photo-electrons out of metal surface can not be explained by particle nature of light/electromagnetic waves.
(E) Existence of threshold wavelength can not be explained by wave nature of light/ electromagnetic waves.
Choose the correct answer from the options given below :
An electron (mass $$\mathrm{m}$$) with an initial velocity $$\vec{v}=v_{0} \hat{i}\left(v_{0}>0\right)$$ is moving in an electric field $$\vec{E}=-E_{0} \hat{i}\left(E_{0}>0\right)$$ where $$E_{0}$$ is constant. If at $$\mathrm{t}=0$$ de Broglie wavelength is $$\lambda_{0}=\frac{h}{m v_{0}}$$, then its de Broglie wavelength after time t is given by
A parallel beam of light of wavelength $$900 \mathrm{~nm}$$ and intensity $$100 \,\mathrm{Wm}^{-2}$$ is incident on a surface perpendicular to the beam. The number of photons crossing $$1 \mathrm{~cm}^{2}$$ area perpendicular to the beam in one second is :
The ratio of wavelengths of proton and deuteron accelerated by potential Vp and Vd is 1 : $$\sqrt2$$. Then the ratio of Vp to Vd will be :
A metal exposed to light of wavelength $$800 \mathrm{~nm}$$ and and emits photoelectrons with a certain kinetic energy. The maximum kinetic energy of photo-electron doubles when light of wavelength $$500 \mathrm{~nm}$$ is used. The workfunction of the metal is : (Take hc $$=1230 \,\mathrm{eV}-\mathrm{nm}$$ ).
A source of monochromatic light liberates 9 $$\times$$ 1020 photon per second with wavelength 600 nm when operated at 400 W. The number of photons emitted per second with wavelength of 800 nm by the source of monochromatic light operating at same power will be :
The electric field at a point associated with a light wave is given by
E = 200 [sin (6 $$\times$$ 1015)t + sin (9 $$\times$$ 1015)t] Vm$$-$$1
Given : h = 4.14 $$\times$$ 10$$-$$15 eVs
If this light falls on a metal surface having a work function of 2.50 eV, the maximum kinetic energy of the photoelectrons will be
Given below are two statements : one is labelled as Assertion A and the other is labelled as Reason R :
Assertion A : The photoelectric effect does not takes place, if the energy of the incident radiation is less than the work function of a metal.
Reason R : Kinetic energy of the photoelectrons is zero, if the energy of the incident radiation is equal to the work function of a metal.
In the light of the above statements, choose the most appropriate answer from the options given below.
Let K1 and K2 be the maximum kinetic energies of photo-electrons emitted when two monochromatic beams of wavelength $$\lambda$$1 and $$\lambda$$2, respectively are incident on a metallic surface. If $$\lambda$$1 = 3$$\lambda$$2 then :
The de Broglie wavelengths for an electron and a photon are $$\lambda$$e and $$\lambda$$p respectively. For the same kinetic energy of electron and photon, which of the following presents the correct relation between the de Broglie wavelengths of two ?
An $$\alpha$$ particle and a carbon 12 atom has same kinetic energy K. The ratio of their de-Broglie wavelengths $$({\lambda _\alpha }:{\lambda _{C12}})$$ is :
A metal surface is illuminated by a radiation of wavelength 4500 $$\mathop A\limits^o $$. The ejected photo-electron enters a constant magnetic field of 2 mT making an angle of 90$$^\circ$$ with the magnetic field. If it starts revolving in a circular path of radius 2 mm, the work function of the metal is approximately :
An electron with speed v and a photon with speed c have the same de-Broglie wavelength. If the kinetic energy and momentum of electron are Ee and pe and that of photon are Eph and pph respectively. Which of the following is correct?
A proton, a neutron, an electron and an $$\alpha$$ particle have same energy. If $$\lambda$$p, $$\lambda$$n, $$\lambda$$e and $$\lambda$$a are the de Broglie's wavelengths of proton, neutron, electron and $$\alpha$$ particle respectively, then choose the correct relation from the following :
Given below are two statements :
Statement I : Davisson-Germer experiment establishes the wave nature of electrons.
Statement II : If electrons have wave nature, they can interfere and show diffraction.
In the light of the above statements choose the correct answer from the option given below :
The light of two different frequencies whose photons have energies 3.8 eV and 1.4 eV respectively, illuminate a metallic surface whose work function is 0.6 eV successively. The ratio of maximum speeds of emitted electrons for the two frequencies respectively will be :
[me = mass of electron = 9 $$\times$$ 10$$-$$31 kg, h = Planck constant = 6.6 $$\times$$ 6.6 $$\times$$ 10$$-$$34 Js, kB = Boltzmann constant = 1.38 $$\times$$ 10$$-$$23 JK$$-$$1]
Assertion A : An electron microscope can achieve better resolving power than an optical microscope.
Reason R : The de Broglie's wavelength of the electrons emitted from an electron gun is much less than wavelength of visible light.
In the light of the above statements, choose the correct answer from the options given below :
Statement I : Two photons having equal linear momenta have equal wavelengths.
Statement II : If the wavelength of photon is decreased, then the momentum and energy of a photon will also decrease.
In the light of the above statements, choose the correct answer from the options given below.
(Given : nitrogen molecule weight : 4.64 $$ \times $$ 10–26 kg,
Boltzman constant: 1.38 $$ \times $$ 10–23 J/K,
Planck constant : 6.63 $$ \times $$ 10–34 J.s)

(Plancks constant h = 6.62 × 10–34 J.s)
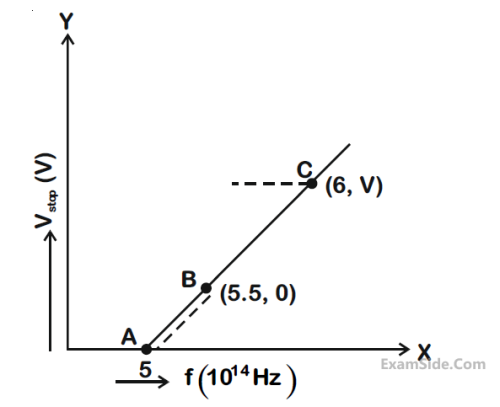
(Given: Planck’s constant (h) = 6.63 × 10–34 Js, electron charges e = 1.6 × 10–19 C)

Given E (in eV) = 1237/$$\lambda $$ (in nm)
Given, E (in eV) = 12375/$$\lambda $$(inÅ)
(Take c = 3 $$ \times $$ 108 ms$$-$$1, h = 6.6 $$ \times $$ 10$$-$$34J-s)
(Energy of photon n = $${{1240} \over {\lambda (in\,mm)}}$$eV)
[Take Planck's constant h $$=$$ 6.62 $$ \times $$ 10$$-$$34 Js]

Statement 1 : Davisson - Germer experiment established the wave nature of electrons.
Statement 2 : If electrons have wave nature, they can interfere and show diffraction.
Statement - $$1$$ : A metallic surface is irradiated by a monochromatic light of frequency $$v > {v_0}$$ (the threshold frequency). The maximum kinetic energy and the stopping potential are $${K_{\max }}$$ and $${V_0}$$ respectively. If the frequency incident on the surface is doubled, both the $${K_{\max }}$$ anmd $${V_0}$$ are also doubled.
Statement - $$2$$ : The maximum kinetic energy and the stopping potential of photoelectrons emitted from a surface are linearly dependent on the frequency of incident light.
Statement - $$2$$ : Photoelectrons are emitted with speeds ranging from zero to a maximum value because of the range of frequencies present in the incident light.
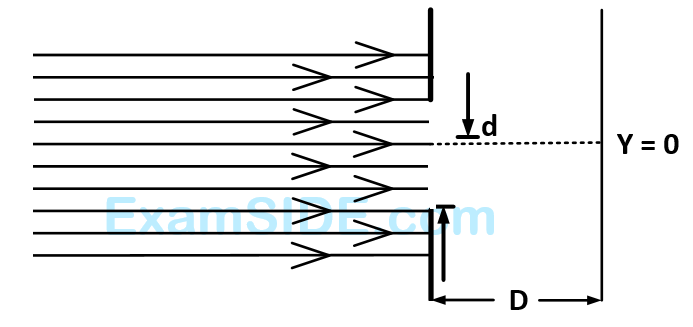
Which of the following graphs can be expected to represent the number of electrons $$'N'$$ detected as a function of the detector position $$'y'\left( {y = 0} \right.$$ corresponds to the middle of the slit$$\left. \, \right)$$
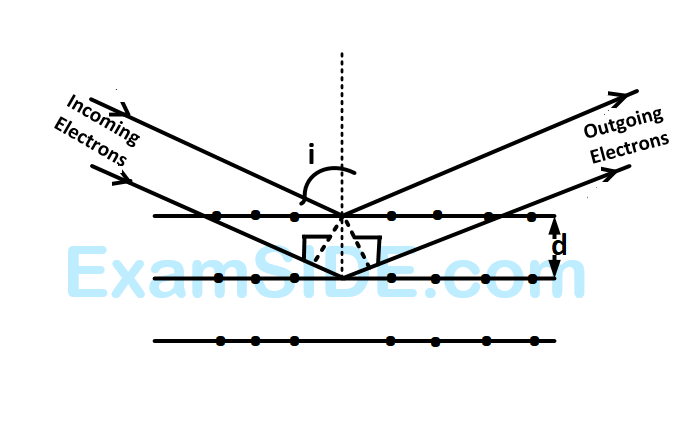
If a strong diffraction peak is observed when electrons are incident at an angle $$'i'$$ from the normal to the crystal planes with distance $$'d'$$ between them (see figure), de Broglie wavelength $${\lambda _{dB}}$$ of electrons can be calculated by the relationship ($$n$$ is an integer)

Electrons accelerated by potential $$V$$ are diffracted from a crystal. If $$d = 1\mathop A\limits^ \circ $$ and $$i = {30^ \circ },\,\,\,V$$ should be about
$$\left( {h = 6.6 \times {{10}^{ - 34}}Js,{m_e} = 9.1 \times {{10}^{ - 31}}kg,\,e = 1.6 \times {{10}^{ - 19}}C} \right)$$