Laws of Motion · Physics · JEE Main
MCQ (Single Correct Answer)
A body of mass 2 kg moving with velocity of $ \vec{v}_{in} = 3 \hat{i} + 4 \hat{j} \text{ ms}^{-1} $ enters into a constant force field of 6N directed along positive z-axis. If the body remains in the field for a period of $ \frac{5}{3} $ seconds, then velocity of the body when it emerges from force field is.
An object with mass 500 g moves along x-axis with speed $v = 4\sqrt{x}$ m/s. The force acting on the object is :
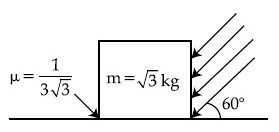
A cubic block of mass $m$ is sliding down on an inclined plane at $60^{\circ}$ with an acceleration of $\frac{g}{2}$, the value of coefficient of kinetic friction is
A body of mass $m$ is suspended by two strings making angles $\theta_1$ and $\theta_2$ with the horizontal ceiling with tensions $T_1$ and $T_2$ simultaneously. $T_1$ and $T_2$ are related by $T_1=\sqrt{3} T_2$, the angles $\theta_1$ and $\theta_2$ are
A block of mass 1 kg , moving along $x$ with speed $v_i=10 \mathrm{~m} / \mathrm{s}$ enters a rough region ranging from $x=0.1 \mathrm{~m}$ to $x=1.9 \mathrm{~m}$. The retarding force acting on the block in this range is $\mathrm{F}_{\mathrm{r}}=-\mathrm{kr} \mathrm{N}$, with k $=10 \mathrm{~N} / \mathrm{m}$. Then the final speed of the block as it crosses rough region is.

A body of mass 1 kg is suspended with the help of two strings making angles as shown in figure. Magnitudes of tensions $\mathrm{T}_1$ and $\mathrm{T}_2$, respectively, are (in N ) :
(Take acceleration due to gravity $10 \mathrm{~m} / \mathrm{s}^2$ )
A balloon and its content having mass M is moving up with an acceleration ‘a’. The mass that must be released from the content so that the balloon starts moving up with an acceleration ‘3a’ will be
(Take ‘g’ as acceleration due to gravity)
A $$1 \mathrm{~kg}$$ mass is suspended from the ceiling by a rope of length $$4 \mathrm{~m}$$. A horizontal force '$$F$$' is applied at the mid point of the rope so that the rope makes an angle of $$45^{\circ}$$ with respect to the vertical axis as shown in figure. The magnitude of $$F$$ is :
(Assume that the system is in equilibrium and $$g=10 \mathrm{~m} / \mathrm{s}^2$$)

A heavy iron bar, of weight $$W$$ is having its one end on the ground and the other on the shoulder of a person. The bar makes an angle $$\theta$$ with the horizontal. The weight experienced by the person is :
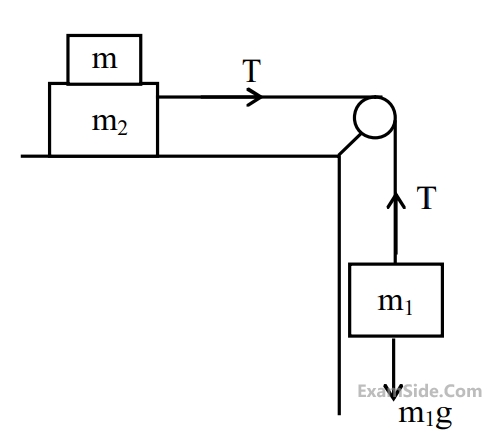
A light unstretchable string passing over a smooth light pulley connects two blocks of masses $$m_1$$ and $$m_2$$. If the acceleration of the system is $$\frac{g}{8}$$, then the ratio of the masses $$\frac{m_2}{m_1}$$ is :
A given object takes $$\mathrm{n}$$ times the time to slide down $$45^{\circ}$$ rough inclined plane as it takes the time to slide down an identical perfectly smooth $$45^{\circ}$$ inclined plane. The coefficient of kinetic friction between the object and the surface of inclined plane is :
A player caught a cricket ball of mass $$150 \mathrm{~g}$$ moving at a speed of $$20 \mathrm{~m} / \mathrm{s}$$. If the catching process is completed in $$0.1 \mathrm{~s}$$, the magnitude of force exerted by the ball on the hand of the player is:
A body of weight $$200 \mathrm{~N}$$ is suspended from a tree branch through a chain of mass $$10 \mathrm{~kg}$$. The branch pulls the chain by a force equal to (if $$\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$$) :
A light string passing over a smooth light pulley connects two blocks of masses $$m_1$$ and $$m_2\left(\right.$$ where $$\left.m_2>m_1\right)$$. If the acceleration of the system is $$\frac{g}{\sqrt{2}}$$, then the ratio of the masses $$\frac{m_1}{m_2}$$ is:
A particle moves in $$x$$-$$y$$ plane under the influence of a force $$\vec{F}$$ such that its linear momentum is $$\overrightarrow{\mathrm{p}}(\mathrm{t})=\hat{i} \cos (\mathrm{kt})-\hat{j} \sin (\mathrm{kt})$$. If $$\mathrm{k}$$ is constant, the angle between $$\overrightarrow{\mathrm{F}}$$ and $$\overrightarrow{\mathrm{p}}$$ will be :
A heavy box of mass $$50 \mathrm{~kg}$$ is moving on a horizontal surface. If co-efficient of kinetic friction between the box and horizontal surface is 0.3 then force of kinetic friction is :
A wooden block of mass $$5 \mathrm{~kg}$$ rests on a soft horizontal floor. When an iron cylinder of mass $$25 \mathrm{~kg}$$ is placed on the top of the block, the floor yields and the block and the cylinder together go down with an acceleration of $$0.1 \mathrm{~ms}^{-2}$$. The action force of the system on the floor is equal to :
A $$2 \mathrm{~kg}$$ brick begins to slide over a surface which is inclined at an angle of $$45^{\circ}$$ with respect to horizontal axis. The co-efficient of static friction between their surfaces is:
A wooden block, initially at rest on the ground, is pushed by a force which increases linearly with time $$t$$. Which of the following curve best describes acceleration of the block with time :
(Consider that the string is massless and unstretchable and the pulley is also massless and frictionless) :


A block of mass $$5 \mathrm{~kg}$$ is placed on a rough inclined surface as shown in the figure. If $$\overrightarrow{F_1}$$ is the force required to just move the block up the inclined plane and $$\overrightarrow{F_2}$$ is the force required to just prevent the block from sliding down, then the value of $$\left|\overrightarrow{F_1}\right|-\left|\overrightarrow{F_2}\right|$$ is : [Use $$\left.\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2\right]$$
A light string passing over a smooth light fixed pulley connects two blocks of masses $$m_1$$ and $$m_2$$. If the acceleration of the system is $$g / 8$$, then the ratio of masses is:

In the given arrangement of a doubly inclined plane two blocks of masses $$M$$ and $$m$$ are placed. The blocks are connected by a light string passing over an ideal pulley as shown. The coefficient of friction between the surface of the plane and the blocks is 0.25. The value of $$m$$, for which $$M=10 \mathrm{~kg}$$ will move down with an acceleration of $$2 \mathrm{~m} / \mathrm{s}^2$$, is: (take $$\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$$ and $$\left.\tan 37^{\circ}=3 / 4\right)$$

A block of mass $$m$$ is placed on a surface having vertical crossection given by $$y=x^2 / 4$$. If coefficient of friction is 0.5, the maximum height above the ground at which block can be placed without slipping is:
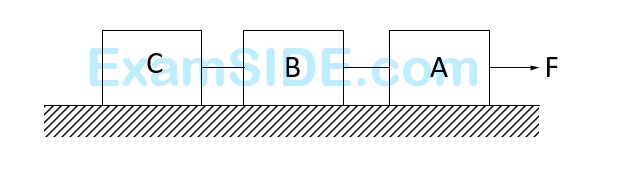
Three blocks $$A, B$$ and $$C$$ are pulled on a horizontal smooth surface by a force of $$80 \mathrm{~N}$$ as shown in figure

The tensions T$$_1$$ and T$$_2$$ in the string are respectively :
All surfaces shown in figure are assumed to be frictionless and the pulleys and the string are light. The acceleration of the block of mass $$2 \mathrm{~kg}$$ is :

Given below are two statements :
Statement (I) : The limiting force of static friction depends on the area of contact and independent of materials.
Statement (II) : The limiting force of kinetic friction is independent of the area of contact and depends on materials.
In the light of the above statements, choose the most appropriate answer from the options given below :
$\vec{r}=\left(10 t \hat{i}+15 t^{2} \hat{j}+7 \hat{k}\right) m$
The direction of net force experienced by the particle is :
Three forces $$F_{1}=10 \mathrm{~N}, F_{2}=8 \mathrm{~N}, \mathrm{~F}_{3}=6 \mathrm{~N}$$ are acting on a particle of mass $$5 \mathrm{~kg}$$. The forces $$\mathrm{F}_{2}$$ and $$\mathrm{F}_{3}$$ are applied perpendicularly so that particle remains at rest. If the force $$F_{1}$$ is removed, then the acceleration of the particle is:
A body of mass $$500 \mathrm{~g}$$ moves along $$\mathrm{x}$$-axis such that it's velocity varies with displacement $$\mathrm{x}$$ according to the relation $$v=10 \sqrt{x} \mathrm{~m} / \mathrm{s}$$ the force acting on the body is:-
At any instant the velocity of a particle of mass $$500 \mathrm{~g}$$ is $$\left(2 t \hat{i}+3 t^{2} \hat{j}\right) \mathrm{ms}^{-1}$$. If the force acting on the particle at $$t=1 \mathrm{~s}$$ is $$(\hat{i}+x \hat{j}) \mathrm{N}$$. Then the value of $$x$$ will be:
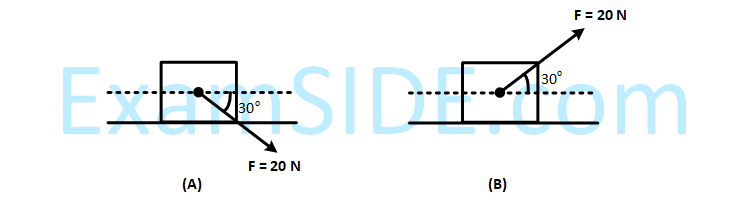
As shown in the figure a block of mass 10 kg lying on a horizontal surface is pulled by a force F acting at an angle $$30^\circ$$, with horizontal. For $$\mu_s=0.25$$, the block will just start to move for the value of F : [Given $$g=10~\mathrm{ms}^{-2}$$]

Figures (a), (b), (c) and (d) show variation of force with time.

The impulse is highest in figure.
A block of mass $$5 \mathrm{~kg}$$ is placed at rest on a table of rough surface. Now, if a force of $$30 \mathrm{~N}$$ is applied in the direction parallel to surface of the table, the block slides through a distance of $$50 \mathrm{~m}$$ in an interval of time $$10 \mathrm{~s}$$. Coefficient of kinetic friction is (given, $$g=10 \mathrm{~ms}^{-2}$$):
(Take acceleration due to gravity $g=10 \mathrm{~ms}^{-2}$ )
As shown in figure, a $$70 \mathrm{~kg}$$ garden roller is pushed with a force of $$\vec{F}=200 \mathrm{~N}$$ at an angle of $$30^{\circ}$$ with horizontal. The normal reaction on the roller is
(Given $$\mathrm{g=10~m~s^{-2}}$$)

A force acts for 20 s on a body of mass 20 kg, starting from rest, after which the force ceases and then body describes 50 m in the next 10 s. The value of force will be:
The time taken by an object to slide down 45$$^\circ$$ rough inclined plane is n times as it takes to slide down a perfectly smooth 45$$^\circ$$ incline plane. The coefficient of kinetic friction between the object and the incline plane is :
A block of mass $m$ slides down the plane inclined at angle $$30^{\circ}$$ with an acceleration $$\frac{g}{4}$$. The value of coefficient of kinetic friction will be:
Consider a block kept on an inclined plane (incline at 45$$^\circ$$) as shown in the figure. If the force required to just push it up the incline is 2 times the force required to just prevent it from sliding down, the coefficient of friction between the block and inclined plane($$\mu$$) is equal to :

As per given figure, a weightless pulley P is attached on a double inclined frictionless surfaces. The tension in the string (massless) will be (if g = 10 m/s$$^2$$)

Given below are two statements :
Statement I : An elevator can go up or down with uniform speed when its weight is balanced with the tension of its cable.
Statement II : Force exerted by the floor of an elevator on the foot of a person standing on it is more than his/her weight when the elevator goes down with increasing speed.
In the light of the above statements, choose the correct answer from the options given below :
Two bodies of masses $$m_{1}=5 \mathrm{~kg}$$ and $$m_{2}=3 \mathrm{~kg}$$ are connected by a light string going over a smooth light pulley on a smooth inclined plane as shown in the figure. The system is at rest. The force exerted by the inclined plane on the body of mass $$\mathrm{m}_{1}$$ will be : [Take $$\left.\mathrm{g}=10 \mathrm{~ms}^{-2}\right]$$

A uniform metal chain of mass m and length 'L' passes over a massless and frictionless pulley. It is released from rest with a part of its length 'l' is hanging on one side and rest of its length '$$\mathrm{L}-l$$' is hanging on the other side of the pully. At a certain point of time, when $$l=\frac{L}{x}$$, the acceleration of the chain is $$\frac{g}{2}$$. The value of x is __________.

A block of mass M slides down on a rough inclined plane with constant velocity. The angle made by the incline plane with horizontal is $$\theta$$. The magnitude of the contact force will be :
A block 'A' takes 2 s to slide down a frictionless incline of 30$$^\circ$$ and length 'l', kept inside a lift going up with uniform velocity 'v'. If the incline is changed to 45$$^\circ$$, the time taken by the block, to slide down the incline, will be approximately :
A bag is gently dropped on a conveyor belt moving at a speed of $$2 \mathrm{~m} / \mathrm{s}$$. The coefficient of friction between the conveyor belt and bag is $$0.4$$. Initially, the bag slips on the belt before it stops due to friction. The distance travelled by the bag on the belt during slipping motion, is : [Take $$\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{-2}$$ ]
Two masses $$M_{1}$$ and $$M_{2}$$ are tied together at the two ends of a light inextensible string that passes over a frictionless pulley. When the mass $$M_{2}$$ is twice that of $$M_{1}$$, the acceleration of the system is $$a_{1}$$. When the mass $$M_{2}$$ is thrice that of $$M_{1}$$, the acceleration of the system is $$a_{2}$$. The ratio $$\frac{a_{1}}{a_{2}}$$ will be :

Three masses $$M=100 \mathrm{~kg}, \mathrm{~m}_{1}=10 \mathrm{~kg}$$ and $$\mathrm{m}_{2}=20 \mathrm{~kg}$$ are arranged in a system as shown in figure. All the surfaces are frictionless and strings are inextensible and weightless. The pulleys are also weightless and frictionless. A force $$\mathrm{F}$$ is applied on the system so that the mass $$\mathrm{m}_{2}$$ moves upward with an acceleration of $$2 \mathrm{~ms}^{-2}$$. The value of $$\mathrm{F}$$ is :
( Take $$\mathrm{g}=10 \mathrm{~ms}^{-2}$$ )

A monkey of mass $$50 \mathrm{~kg}$$ climbs on a rope which can withstand the tension (T) of $$350 \mathrm{~N}$$. If monkey initially climbs down with an acceleration of $$4 \mathrm{~m} / \mathrm{s}^{2}$$ and then climbs up with an acceleration of $$5 \mathrm{~m} / \mathrm{s}^{2}$$. Choose the correct option $$\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)$$.
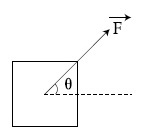
For a free body diagram shown in the figure, the four forces are applied in the 'x' and 'y' directions. What additional force must be applied and at what angle with positive x-axis so that the net acceleration of body is zero?

A 2 kg block is pushed against a vertical wall by applying a horizontal force of 50 N. The coefficient of static friction between the block and the wall is 0.5. A force F is also applied on the block vertically upward (as shown in figure). The maximum value of F applied, so that the block does not move upward, will be :
(Given : g = 10 ms$$-$$2)

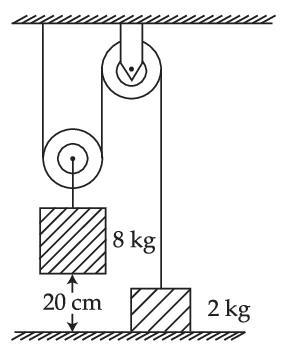
A block of mass 40 kg slides over a surface, when a mass of 4 kg is suspended through an inextensible massless string passing over frictionless pulley as shown below.
The coefficient of kinetic friction between the surface and block is 0.02. The acceleration of block is. (Given g = 10 ms$$-$$2.)

A block of mass M placed inside a box descends vertically with acceleration 'a'. The block exerts a force equal to one-fourth of its weight on the floor of the box. The value of 'a' will be
A block of mass 2 kg moving on a horizontal surface with speed of 4 ms$$-$$1 enters a rough surface ranging from x = 0.5 m to x = 1.5 m. The retarding force in this range of rough surface is related to distance by F = $$-$$kx where k = 12 Nm$$-$$1. The speed of the block as it just crosses the rough surface will be :
A system of two blocks of masses m = 2 kg and M = 8 kg is placed on a smooth table as shown in figure. The coefficient of static friction between two blocks is 0.5. The maximum horizontal force F that can be applied to the block of mass M so that the blocks move together will be :

In the arrangement shown in figure a1, a2, a3 and a4 are the accelerations of masses m1, m2, m3 and m4 respectively. Which of the following relation is true for this arrangement?

A person is standing in an elevator. In which situation, he experiences weight loss?
An object of mass 5 kg is thrown vertically upwards from the ground. The air resistance produces a constant retarding force of 10 N throughout the motion. The ratio of time of ascent to the time of descent will be equal to : [Use g = 10 ms$$-$$2].
A block of mass 10 kg starts sliding on a surface with an initial velocity of 9.8 ms$$-$$1. The coefficient of friction between the surface and block is 0.5. The distance covered by the block before coming to rest is :
[use g = 9.8 ms$$-$$2]


The correct applied force vs distance graph will be :
If three forces $${\overrightarrow F _1},{\overrightarrow F _2}$$ and $${\overrightarrow F _3}$$ are represented by three sides of a triangle and $${\overrightarrow F _1} + {\overrightarrow F _2} = - {\overrightarrow F _3}$$, then these three forces are concurrent forces and satisfy the condition for equilibrium.
Statement : 2
A triangle made up of three forces $${\overrightarrow F _1}$$, $${\overrightarrow F _2}$$ and $${\overrightarrow F _3}$$ as its sides taken in the same order, satisfy the condition for translatory equilibrium.
In the light of the above statements, choose the most appropriate answer from the options given below :
$$F = {F_0}\left[ {1 - {{\left( {{{t - T} \over T}} \right)}^2}} \right]$$
Where F0 and T are constants. The force acts only for the time interval 2T. The velocity v of the particle after time 2T is :

(g is acceleration due to gravity)
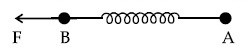
$$\overrightarrow F = k\left( {{v_y}\widehat i + {v_x}\widehat j} \right)$$ , where vx and vy are the
x and y components of its velocity $$\overrightarrow v $$ . If $$\overrightarrow a $$ is the
acceleration of the particle, then
which of the following statements is true for the particle?
(g = 10 ms–2)
increases at a rate $${{dM\left( t \right)} \over {dt}}$$ = bv2(t), where v(t) is its instantaneous velocity. The instantaneous acceleration of the satellite is :
[Take g = 10 m/s2]



Given in the figure are two blocks $$A$$ and $$B$$ of weight 20 N and 100 N, respectively. These are being pressed against a wall by a force $$F$$ as shown. If the coefficient of friction between the blocks is 0.1 and between block $$B$$ and the wall is 0.15, the frictional force applied by the wall on block $$B$$ is :
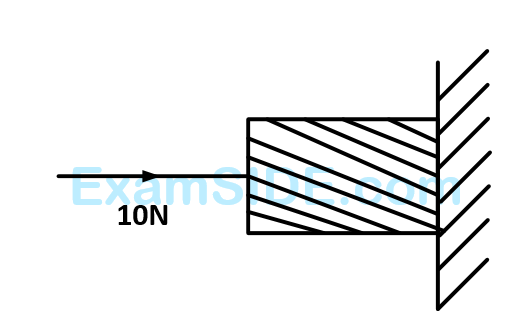
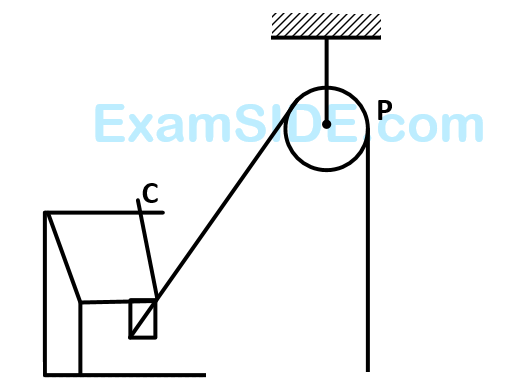
Numerical
Three blocks $$\mathrm{M_1, M_2, M_3}$$ having masses $$4 \mathrm{~kg}, 6 \mathrm{~kg}$$ and $$10 \mathrm{~kg}$$ respectively are hanging from a smooth pully using rope 1, 2 and 3 as shown in figure. The tension in the rope $$\mathrm{1, T_1}$$ when they are moving upward with acceleration of $$2 \mathrm{~ms}^{-2}$$ is __________ $$\mathrm{N}$$ (if $$\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$$).

Two forces $$\overline{\mathrm{F}}_1$$ and $$\overline{\mathrm{F}}_2$$ are acting on a body. One force has magnitude thrice that of the other force and the resultant of the two forces is equal to the force of larger magnitude. The angle between $$\vec{F}_1$$ and $$\vec{F}_2$$ is $$\cos ^{-1}\left(\frac{1}{n}\right)$$. The value of $$|n|$$ is _______.
Two inclined planes are placed as shown in figure. A block is projected from the Point A of inclined plane AB along its surface with a velocity just sufficient to carry it to the top Point B at a height 10 m. After reaching the Point B the block slides down on inclined plane BC. Time it takes to reach to the point C from point A is $$t(\sqrt{2}+1)$$ s. The value of t is ___________.
(use $$\mathrm{~g}=10 \mathrm{~m} / \mathrm{s}^{2}$$ )

Four forces are acting at a point $$\mathrm{P}$$ in equilibrium as shown in figure. The ratio of force $$\mathrm{F}_{1}$$ to $$\mathrm{F}_{2}$$ is $$1: x$$ where $$x=$$ _____________.

A hanging mass M is connected to a four times bigger mass by using a string-pulley arrangement, as shown in the figure. The bigger mass is placed on a horizontal ice-slab and being pulled by 2 Mg force. In this situation, tension in the string is $${x \over 5}$$ Mg for x = ______________. Neglect mass of the string and friction of the block (bigger mass) with ice slab.
(Given g = acceleration due to gravity)

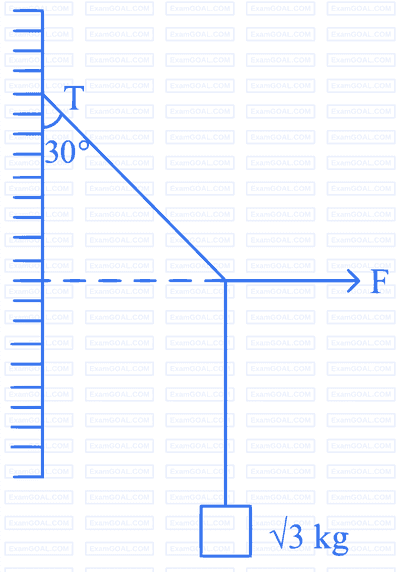
A mass of 10 kg is suspended vertically by a rope of length 5 m from the roof. A force of 30 N is applied at the middle point of rope in horizontal direction. The angle made by upper half of the rope with vertical is $$\theta$$ = tan$$-$$1 (x $$\times$$ 10$$-$$1). The value of x is ____________.
(Given, g = 10 m/s2)
A system to 10 balls each of mass 2 kg are connected via massless and unstretchable string. The system is allowed to slip over the edge of a smooth table as shown in figure. Tension on the string between the 7th and 8th ball is __________ N when 6th ball just leaves the table.

A block of mass 200 g is kept stationary on a smooth inclined plane by applying a minimum horizontal force F = $$\sqrt{x}$$N as shown in figure.

The value of x = _____________.
A force on an object of mass 100 g is $$\left( {10\widehat i + 5\widehat j} \right)$$ N. The position of that object at t = 2 s is $$\left( {a\widehat i + b\widehat j} \right)$$ m after starting from rest. The value of $${a \over b}$$ will be ___________.
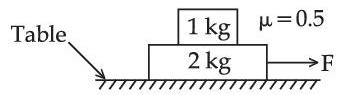
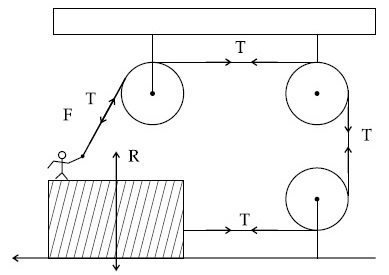
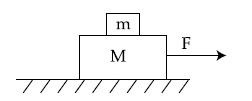
[g = 10 m/s2; sin60$$^\circ$$ = $${{\sqrt 3 } \over 2}$$; cos60$$^\circ$$ = $${1 \over 2}$$]