Work Power & Energy · Physics · JEE Main
MCQ (Single Correct Answer)
Which one of the following forces cannot be expressed in terms of potential energy?
An object of mass 1000 g experiences a time dependent force $\vec{F}=\left(2 t \hat{i}+3 t^2 \hat{j}\right) N$. The power generated by the force at time $t$ is:
A block of mass 25 kg is pulled along a horizontal surface by a force at an angle $45^{\circ}$ with the horizontal. The friction coefficient between the block and the surface is 0.25 . The block travels at a uniform velocity. The work done by the applied force during a displacement of 5 m of the block is :
A sand dropper drops sand of mass m(t) on a conveyer belt at a rate proportional to the square root of speed (v) of the belt, i.e., $\frac{dm}{dt} \propto \sqrt{v}$. If P is the power delivered to run the belt at constant speed then which of the following relationship is true?
A bead of mass ' $m$ ' slides without friction on the wall of a vertical circular hoop of radius ' $R$ ' as shown in figure. The bead moves under the combined action of gravity and a massless spring (k) attached to the bottom of the hoop. The equilibrium length of the spring is ' $R$ '. If the bead is released from top of the hoop with (negligible) zero initial speed, velocity of bead, when the length of spring becomes ' $R$ ', would be (spring constant is ' $k$ ', $g$ is accleration due to gravity)

Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason $\mathbf{R}$
Assertion A: In a central force field, the work done is independent of the path chosen.
Reason R: Every force encountered in mechanics does not have an associated potential energy.
In the light of the above statements, choose the most appropriate answer from the options given below
A force $\mathrm{F}=\alpha+\beta \mathrm{x}^2$ acts on an object in the x -direction. The work done by the force is 5 J when the object is displaced by 1 m . If the constant $\alpha=1 \mathrm{~N}$ then $\beta$ will be
A ball having kinetic energy KE, is projected at an angle of $60^{\circ}$ from the horizontal. What will be the kinetic energy of ball at the highest point of its flight?
A force $\overrightarrow{\mathrm{F}}=2 \hat{i}+\mathrm{b} \hat{j}+\hat{k}$ is applied on a particle and it undergoes a displacement $\hat{i}-2 \hat{j}-\hat{k}$ What will be the value of $b$, if work done on the particle is zero.
A particle of mass $$m$$ moves on a straight line with its velocity increasing with distance according to the equation $$v=\alpha \sqrt{x}$$, where $$\alpha$$ is a constant. The total work done by all the forces applied on the particle during its displacement from $$x=0$$ to $$x=\mathrm{d}$$, will be :

A block is simply released from the top of an inclined plane as shown in the figure above. The maximum compression in the spring when the block hits the spring is :
Three bodies A, B and C have equal kinetic energies and their masses are $$400 \mathrm{~g}, 1.2 \mathrm{~kg}$$ and $$1.6 \mathrm{~kg}$$ respectively. The ratio of their linear momenta is :
When kinetic energy of a body becomes 36 times of its original value, the percentage increase in the momentum of the body will be :
A bullet of mass $$50 \mathrm{~g}$$ is fired with a speed $$100 \mathrm{~m} / \mathrm{s}$$ on a plywood and emerges with $$40 \mathrm{~m} / \mathrm{s}$$. The percentage loss of kinetic energy is :
Four particles $$A, B, C, D$$ of mass $$\frac{m}{2}, m, 2 m, 4 m$$, have same momentum, respectively. The particle with maximum kinetic energy is :
A body is moving unidirectionally under the influence of a constant power source. Its displacement in time t is proportional to :
A body of mass $$50 \mathrm{~kg}$$ is lifted to a height of $$20 \mathrm{~m}$$ from the ground in the two different ways as shown in the figures. The ratio of work done against the gravity in both the respective cases, will be :

A body of $$m \mathrm{~kg}$$ slides from rest along the curve of vertical circle from point $$A$$ to $$B$$ in friction less path. The velocity of the body at $$B$$ is:

(given, $$R=14 \mathrm{~m}, g=10 \mathrm{~m} / \mathrm{s}^2$$ and $$\sqrt{2}=1.4$$)
If a rubber ball falls from a height $$h$$ and rebounds upto the height of $$h / 2$$. The percentage loss of total energy of the initial system as well as velocity ball before it strikes the ground, respectively, are :
A body of mass $$2 \mathrm{~kg}$$ begins to move under the action of a time dependent force given by $$\vec{F}=\left(6 t \hat{i}+6 t^2 \hat{j}\right) N$$. The power developed by the force at the time $$t$$ is given by:
A block of mass $$1 \mathrm{~kg}$$ is pushed up a surface inclined to horizontal at an angle of $$60^{\circ}$$ by a force of $$10 \mathrm{~N}$$ parallel to the inclined surface as shown in figure. When the block is pushed up by $$10 \mathrm{~m}$$ along inclined surface, the work done against frictional force is :
$$\left[g=10 \mathrm{~m} / \mathrm{s}^2\right]$$

A particle is placed at the point $$A$$ of a frictionless track $$A B C$$ as shown in figure. It is gently pushed towards right. The speed of the particle when it reaches the point B is :
(Take $$g=10 \mathrm{~m} / \mathrm{s}^2$$).

A bob of mass '$$m$$' is suspended by a light string of length '$$L$$'. It is imparted a minimum horizontal velocity at the lowest point $$A$$ such that it just completes half circle reaching the top most position B. The ratio of kinetic energies $$\frac{(K . E)_A}{(K . E)_B}$$ is :

A block of mass $$100 \mathrm{~kg}$$ slides over a distance of $$10 \mathrm{~m}$$ on a horizontal surface. If the co-efficient of friction between the surfaces is 0.4, then the work done against friction $$(\operatorname{in} J$$) is :
The potential energy function (in $$J$$ ) of a particle in a region of space is given as $$U=\left(2 x^2+3 y^3+2 z\right)$$. Here $$x, y$$ and $$z$$ are in meter. The magnitude of $$x$$-component of force (in $$N$$ ) acting on the particle at point $$P(1,2,3) \mathrm{m}$$ is :
A ball suspended by a thread swings in a vertical plane so that its magnitude of acceleration in the extreme position and lowest position are equal. The angle $$(\theta)$$ of thread deflection in the extreme position will be :
A bullet is fired into a fixed target looses one third of its velocity after travelling $$4 \mathrm{~cm}$$. It penetrates further $$\mathrm{D} \times 10^{-3} \mathrm{~m}$$ before coming to rest. The value of $$\mathrm{D}$$ is :
The ratio of powers of two motors is $$\frac{3 \sqrt{x}}{\sqrt{x}+1}$$, that are capable of raising $$300 \mathrm{~kg}$$ water in 5 minutes and $$50 \mathrm{~kg}$$ water in 2 minutes respectively from a well of $$100 \mathrm{~m}$$ deep. The value of $$x$$ will be
Two bodies are having kinetic energies in the ratio 16 : 9. If they have same linear momentum, the ratio of their masses respectively is :
Given below are two statements:
Statement I : A truck and a car moving with same kinetic energy are brought to rest by applying breaks which provide equal retarding forces. Both come to rest in equal distance.
Statement II : A car moving towards east takes a turn and moves towards north, the speed remains unchanged. The acceleration of the car is zero.
In the light of given statements, choose the most appropriate answer from the options given below
A bullet of mass $$0.1 \mathrm{~kg}$$ moving horizontally with speed $$400 \mathrm{~ms}^{-1}$$ hits a wooden block of mass $$3.9 \mathrm{~kg}$$ kept on a horizontal rough surface. The bullet gets embedded into the block and moves $$20 \mathrm{~m}$$ before coming to rest. The coefficient of friction between the block and the surface is __________.
(Given $$g=10 \mathrm{~m} / \mathrm{s}^{2}$$ )
Identify the correct statements from the following :
A. Work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket is negative.
B. Work done by gravitational force in lifting a bucket out of a well by a rope tied to the bucket is negative.
C. Work done by friction on a body sliding down an inclined plane is positive.
D. Work done by an applied force on a body moving on a rough horizontal plane with uniform velocity is zero.
E. Work done by the air resistance on an oscillating pendulum is negative.
Choose the correct answer from the options given below :
A stone is projected at angle $$30^{\circ}$$ to the horizontal. The ratio of kinetic energy of the stone at point of projection to its kinetic energy at the highest point of flight will be -
A ball is projected with kinetic energy E, at an angle of $$60^{\circ}$$ to the horizontal. The kinetic energy of this ball at the highest point of its flight will become :
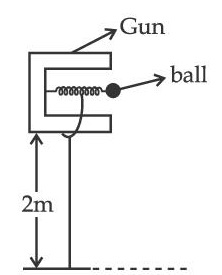
A bullet of mass $$200 \mathrm{~g}$$ having initial kinetic energy $$90 \mathrm{~J}$$ is shot inside a long swimming pool as shown in the figure. If it's kinetic energy reduces to $$40 \mathrm{~J}$$ within $$1 \mathrm{~s}$$, the minimum length of the pool, the bullet has to travel so that it completely comes to rest is

Sand is being dropped from a stationary dropper at a rate of $$0.5 \,\mathrm{kgs}^{-1}$$ on a conveyor belt moving with a velocity of $$5 \mathrm{~ms}^{-1}$$. The power needed to keep the belt moving with the same velocity will be :
As per the given figure, two blocks each of mass $$250 \mathrm{~g}$$ are connected to a spring of spring constant $$2 \,\mathrm{Nm}^{-1}$$. If both are given velocity $$v$$ in opposite directions, then maximum elongation of the spring is :

A bag of sand of mass 9.8 kg is suspended by a rope. A bullet of 200 g travelling with speed 10 ms$$-$$1 gets embedded in it, then loss of kinetic energy will be :
A body of mass $$0.5 \mathrm{~kg}$$ travels on straight line path with velocity $$v=\left(3 x^{2}+4\right) \mathrm{m} / \mathrm{s}$$. The net workdone by the force during its displacement from $$x=0$$ to $$x=2 \mathrm{~m}$$ is :
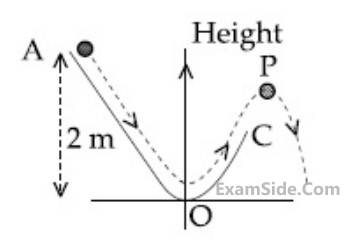
In the given figure, the block of mass m is dropped from the point 'A'. The expression for kinetic energy of block when it reaches point 'B' is

A particle of mass 500 gm is moving in a straight line with velocity v = b x5/2. The work done by the net force during its displacement from x = 0 to x = 4 m is : (Take b = 0.25 m$$-$$3/2 s$$-$$1).
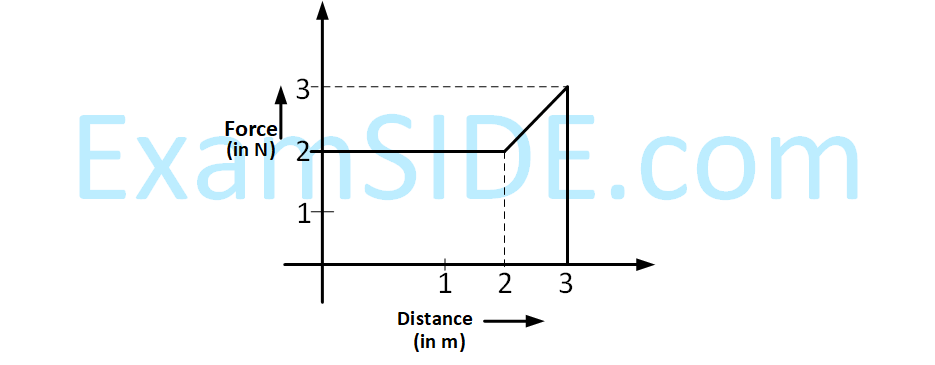
Arrange the four graphs in descending order of total work done; where W1, W2, W3 and W4 are the work done corresponding to figure a, b, c and d respectively.




A particle experiences a variable force $$\overrightarrow F = \left( {4x\widehat i + 3{y^2}\widehat j} \right)$$ in a horizontal x-y plane. Assume distance in meters and force is newton. If the particle moves from point (1, 2) to point (2, 3) in the x-y plane, then Kinetic Energy changes by :
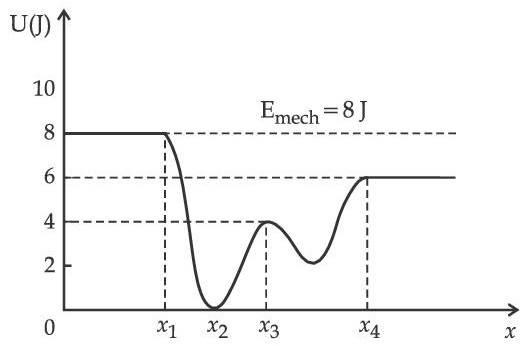
[ where K.E. = kinetic energy ]
(take g = 9.8 ms$$-$$2)
U = $$ - {A \over {{r^6}}} + {B \over {{r^{12}}}}$$,
then at equilibrium, separation between molecules, and the potential energy are :
(1 HP = 746 W, g = 10 ms-2)

The first particle is at a distance r = 1, and the second, at r = 4. The best estimate for the ratio of kinetic energies of the first and the second particle is closest to :

The value of the coefficient of friction $$\mu $$ and the distance $$x$$ $$(=QR),$$ are, respectively close to:

If two springs $${S_1}$$ and $${S_2}$$ of force constants $${k_1}$$ and $${k_2}$$, respectively, are stretched by the same force, it is found that more work is done on spring $${S_1}$$ than on spring $${S_2}$$.
STATEMENT 1: If stretched by the same amount work done on $${S_1}$$, Work done on $${S_1}$$ is more than $${S_2}$$
STATEMENT 2: $${k_1} < {k_2}$$
The total mechanical energy of the particle is $$2J.$$ Then, the maximum speed (in $$m/s$$) is
Numerical
In a hydraulic lift, the surface area of the input piston is 6 cm2 and that of the output piston is 1500 cm2. If 100 N force is applied to the input piston to raise the output piston by 20 cm, then the work done is _______ kJ.
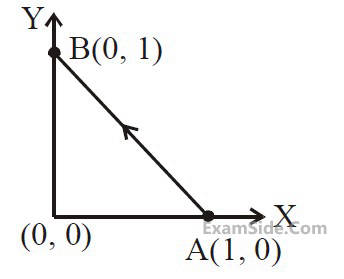
A force $\mathrm{f}=\mathrm{x}^2 \mathrm{y} \hat{\mathrm{i}}+\mathrm{y}^2 \hat{\mathrm{j}}$ acts on a particle in a plane $\mathrm{x}+\mathrm{y}=10$. The work done by this force during a displacement from $(0,0)$ to $(4 \mathrm{~m}, 2 \mathrm{~m})$ is _________ Joule (round off to the nearest integer)
A force $$(3 x^2+2 x-5) \mathrm{N}$$ displaces a body from $$x=2 \mathrm{~m}$$ to $$x=4 \mathrm{~m}$$. Work done by this force is ________ J.
A car accelerates from rest to $$u \mathrm{~m} / \mathrm{s}$$. The energy spent in this process is E J. The energy required to accelerate the car from $$u \mathrm{~m} / \mathrm{s}$$ to $$2 \mathrm{u} \mathrm{m} / \mathrm{s}$$ is $$\mathrm{nE~J}$$. The value of $$\mathrm{n}$$ is ____________.
To maintain a speed of 80 km/h by a bus of mass 500 kg on a plane rough road for 4 km distance, the work done by the engine of the bus will be ____________ KJ. [The coefficient of friction between tyre of bus and road is 0.04.]
A block of mass $$5 \mathrm{~kg}$$ starting from rest pulled up on a smooth incline plane making an angle of $$30^{\circ}$$ with horizontal with an affective acceleration of $$1 \mathrm{~ms}^{-2}$$. The power delivered by the pulling force at $$t=10 \mathrm{~s}$$ from the start is ___________ W.
[use $$\mathrm{g}=10 \mathrm{~ms}^{-2}$$ ]
(calculate the nearest integer value)
A force $$\vec{F}=(2+3 x) \hat{i}$$ acts on a particle in the $$x$$ direction where F is in newton and $$x$$ is in meter. The work done by this force during a displacement from $$x=0$$ to $$x=4 \mathrm{~m}$$, is __________ J.
If the maximum load carried by an elevator is $$1400 \mathrm{~kg}$$ ( $$600 \mathrm{~kg}$$ - Passengers + 800 $$\mathrm{kg}$$ - elevator), which is moving up with a uniform speed of $$3 \mathrm{~m} \mathrm{~s}^{-1}$$ and the frictional force acting on it is $$2000 \mathrm{~N}$$, then the maximum power used by the motor is __________ $$\mathrm{kW}\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}\right)$$
A closed circular tube of average radius 15 cm, whose inner walls are rough, is kept in vertical plane. A block of mass 1 kg just fit inside the tube. The speed of block is 22 m/s, when it is introduced at the top of tube. After completing five oscillations, the block stops at the bottom region of tube. The work done by the tube on the block is __________ J. (Given g = 10 m/s$$^2$$).

A body of mass $$5 \mathrm{~kg}$$ is moving with a momentum of $$10 \mathrm{~kg} \mathrm{~ms}^{-1}$$. Now a force of $$2 \mathrm{~N}$$ acts on the body in the direction of its motion for $$5 \mathrm{~s}$$. The increase in the Kinetic energy of the body is ___________ $$\mathrm{J}$$.
A body is dropped on ground from a height '$$h_{1}$$' and after hitting the ground, it rebounds to a height '$$h_{2}$$'. If the ratio of velocities of the body just before and after hitting ground is 4 , then percentage loss in kinetic energy of the body is $$\frac{x}{4}$$. The value of $$x$$ is ____________.
A particle of mass $$10 \mathrm{~g}$$ moves in a straight line with retardation $$2 x$$, where $$x$$ is the displacement in SI units. Its loss of kinetic energy for above displacement is $$\left(\frac{10}{x}\right)^{-n}$$ J. The value of $$\mathrm{n}$$ will be __________
A block is fastened to a horizontal spring. The block is pulled to a distance $$x=10 \mathrm{~cm}$$ from its equilibrium position (at $$x=0$$) on a frictionless surface from rest. The energy of the block at $$x=5$$ $$\mathrm{cm}$$ is $$0.25 \mathrm{~J}$$. The spring constant of the spring is ___________ $$\mathrm{Nm}^{-1}$$
A force $$\mathrm{F}=\left(5+3 y^{2}\right)$$ acts on a particle in the $$y$$-direction, where $$\mathrm{F}$$ is in newton and $$y$$ is in meter. The work done by the force during a displacement from $$y=2 \mathrm{~m}$$ to $$y=5 \mathrm{~m}$$ is ___________ J.
A small particle moves to position $$5 \hat{i}-2 \hat{j}+\hat{k}$$ from its initial position $$2 \hat{i}+3 \hat{j}-4 \hat{k}$$ under the action of force $$5 \hat{i}+2 \hat{j}+7 \hat{k} \mathrm{~N}$$. The value of work done will be __________ J.
A lift of mass $$\mathrm{M}=500 \mathrm{~kg}$$ is descending with speed of $$2 \mathrm{~ms}^{-1}$$. Its supporting cable begins to slip thus allowing it to fall with a constant acceleration of $$2 \mathrm{~ms}^{-2}$$. The kinetic energy of the lift at the end of fall through to a distance of $$6 \mathrm{~m}$$ will be _____________ $$\mathrm{kJ}$$.
A 0.4 kg mass takes 8s to reach ground when dropped from a certain height 'P' above surface of earth. The loss of potential energy in the last second of fall is __________ J.
(Take g = 10 m/s$$^2$$)
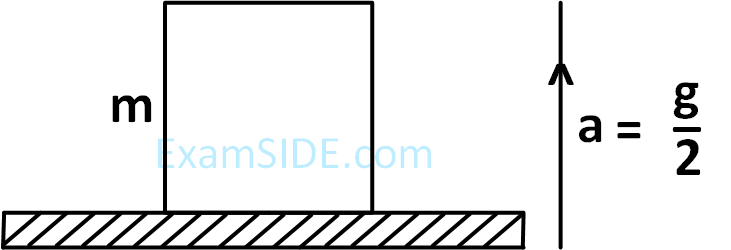
An object of mass 'm' initially at rest on a smooth horizontal plane starts moving under the action of force F = 2N. In the process of its linear motion, the angle $$\theta$$ (as shown in figure) between the direction of force and horizontal varies as $$\theta=\mathrm{k}x$$, where k is a constant and $$x$$ is the distance covered by the object from its initial position. The expression of kinetic energy of the object will be $$E = {n \over k}\sin \theta $$. The value of n is ___________.

A body of mass 1kg begins to move under the action of a time dependent force $$\overrightarrow F = \left( {t\widehat i + 3{t^2}\,\widehat j} \right)$$ N, where $$\widehat i$$ and $$\widehat j$$ are the unit vectors along $$x$$ and $$y$$ axis. The power developed by above force, at the time t = 2s, will be ____________ W.
A spherical body of mass 2 kg starting from rest acquires a kinetic energy of 10000 J at the end of $$\mathrm{5^{th}}$$ second. The force acted on the body is ________ N.
A block of mass '$$\mathrm{m}$$' (as shown in figure) moving with kinetic energy E compresses a spring through a distance $$25 \mathrm{~cm}$$ when, its speed is halved. The value of spring constant of used spring will be $$\mathrm{nE} \,\,\mathrm{Nm}^{-1}$$ for $$\mathrm{n}=$$ _________.

A uniform chain of 6 m length is placed on a table such that a part of its length is hanging over the edge of the table. The system is at rest. The co-efficient of static friction between the chain and the surface of the table is 0.5, the maximum length of the chain hanging from the table is ___________ m.
A 0.5 kg block moving at a speed of 12 ms$$-$$1 compresses a spring through a distance 30 cm when its speed is halved. The spring constant of the spring will be _______________ Nm$$-$$1.
A ball of mass 100 g is dropped from a height h = 10 cm on a platform fixed at the top of a vertical spring (as shown in figure). The ball stays on the platform and the platform is depressed by a distance $${h \over 2}$$. The spring constant is _____________ Nm$$-$$1.
(Use g = 10 ms$$-$$2)

(Assume there is no friction between the block and the hemisphere)
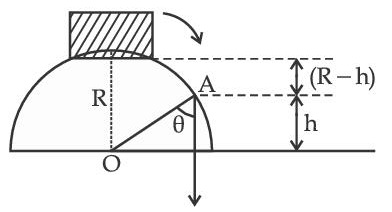
The value of 'x' to the nearest integer is __________.
$$U = {\alpha \over {{r^{10}}}} - {\beta \over {{r^5}}} - 3$$
where, $$\alpha$$ and $$\beta$$ are positive constants. The equilibrium distance between two atoms will be $${\left( {{{2\alpha } \over \beta }} \right)^{{a \over b}}}$$, where a = ___________.
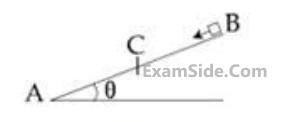
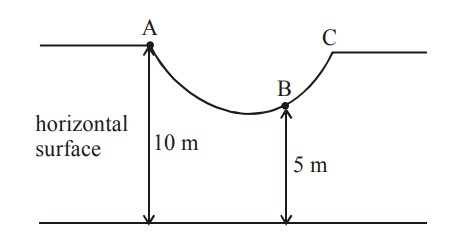
A small block starts slipping down from a point B on an inclined plane AB, which is making an angle $$\theta $$ with the horizontal section BC is smooth and the remaining section CA is rough with a coefficient of friction $$\mu $$. It is found that the block comes to rest as it reaches the bottom (point A) of the inclined plane. If BC = 2AC, the coefficient of friction is given by $$\mu $$ = ktan $$\theta $$ . The value of k is _________.
(Figure drawn is schematic and not to scale; take g = 10 ms-2)