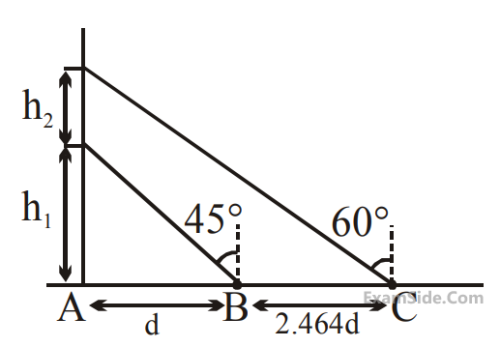
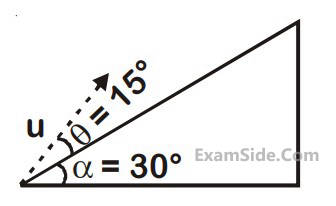
Motion in a Plane · Physics · JEE Main

The position vector of a moving body at any instant of time is given as $\overrightarrow{\mathrm{r}}=\left(5 \mathrm{t}^2 \hat{i}-5 \mathrm{t} \hat{j}\right) \mathrm{m}$. The magnitude and direction of velocity at $t=2 s$ is,

An object of mass ' m ' is projected from origin in a vertical xy plane at an angle $45^{\circ}$ with the $\mathrm{x}-$ axis with an initial velocity $\mathrm{v}_0$. The magnitude and direction of the angular momentum of the object with respect to origin, when it reaches at the maximum height, will be [ g is acceleration due to gravity]

A ball of mass 100 g is projected with velocity $20 \mathrm{~m} / \mathrm{s}$ at $60^{\circ}$ with horizontal. The decrease in kinetic energy of the ball during the motion from point of projection to highest point is

The angle of projection for a projectile to have same horizontal range and maximum height is :

The co-ordinates of a particle moving in $$x$$-$$y$$ plane are given by : $$x=2+4 \mathrm{t}, y=3 \mathrm{t}+8 \mathrm{t}^2$$.

The motion of the particle is :

Projectiles A and B are thrown at angles of $$45^{\circ}$$ and $$60^{\circ}$$ with vertical respectively from top of a $$400 \mathrm{~m}$$ high tower. If their ranges and times of flight are same, the ratio of their speeds of projection $$v_A: v_B$$ is :

[Take $$g=10 \mathrm{~ms}^{-2}$$]

Position of an ant ($$\mathrm{S}$$ in metres) moving in $$\mathrm{Y}$$-$$\mathrm{Z}$$ plane is given by $$S=2 t^2 \hat{j}+5 \hat{k}$$ (where $$t$$ is in second). The magnitude and direction of velocity of the ant at $$\mathrm{t}=1 \mathrm{~s}$$ will be :

A projectile is projected at $$30^{\circ}$$ from horizontal with initial velocity $$40 \mathrm{~ms}^{-1}$$. The velocity of the projectile at $$\mathrm{t}=2 \mathrm{~s}$$ from the start will be : (Given $$g=10 \mathrm{~m} / \mathrm{s}^{2}$$ )

Two projectiles are projected at $$30^{\circ}$$ and $$60^{\circ}$$ with the horizontal with the same speed. The ratio of the maximum height attained by the two projectiles respectively is:

The range of the projectile projected at an angle of 15$$^\circ$$ with horizontal is 50 m. If the projectile is projected with same velocity at an angle of 45$$^\circ$$ with horizontal, then its range will be

The trajectory of projectile, projected from the ground is given by $$y=x-\frac{x^{2}}{20}$$. Where $$x$$ and $$y$$ are measured in meter. The maximum height attained by the projectile will be.

Two projectiles A and B are thrown with initial velocities of $$40 \mathrm{~m} / \mathrm{s}$$ and $$60 \mathrm{~m} / \mathrm{s}$$ at angles $$30^{\circ}$$ and $$60^{\circ}$$ with the horizontal respectively. The ratio of their ranges respectively is $$\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)$$

Given below are two statements : one is labelled as Assertion A and the other is labelled as Reason R

Assertion A : When a body is projected at an angle $$45^{\circ}$$, it's range is maximum.

Reason R : For maximum range, the value of $$\sin 2 \theta$$ should be equal to one.

In the light of the above statements, choose the correct answer from the options given below:

A child stands on the edge of the cliff $$10 \mathrm{~m}$$ above the ground and throws a stone horizontally with an initial speed of $$5 \mathrm{~ms}^{-1}$$. Neglecting the air resistance, the speed with which the stone hits the ground will be $$\mathrm{ms}^{-1}$$ (given, $$g=10 \mathrm{~ms}^{-2}$$ ).

The initial speed of a projectile fired from ground is $$\mathrm{u}$$. At the highest point during its motion, the speed of projectile is $$\frac{\sqrt{3}}{2} u$$. The time of flight of the projectile is :

Two objects are projected with same velocity 'u' however at different angles $$\alpha$$ and $$\beta$$ with the horizontal. If $$\alpha+\beta=90^\circ$$, the ratio of horizontal range of the first object to the 2nd object will be :

The maximum vertical height to which a man can throw a ball is 136 m. The maximum horizontal distance upto which he can throw the same ball is :

At time $$t=0$$ a particle starts travelling from a height $$7 \hat{z} \mathrm{~cm}$$ in a plane keeping z coordinate constant. At any instant of time it's position along the $$\hat{x}$$ and $$\hat{y}$$ directions are defined as $$3 \mathrm{t}$$ and $$5 \mathrm{t}^{3}$$ respectively. At t = 1s acceleration of the particle will be

Two projectiles are thrown with same initial velocity making an angle of $$45^{\circ}$$ and $$30^{\circ}$$ with the horizontal respectively. The ratio of their respective ranges will be :

Two projectiles thrown at $$30^{\circ}$$ and $$45^{\circ}$$ with the horizontal respectively, reach the maximum height in same time. The ratio of their initial velocities is :

A ball is projected from the ground with a speed 15 ms^$$-$$1 at an angle $$\theta$$ with horizontal so that its range and maximum height are equal,
then 'tan $$\theta$$' will be equal to :

At t = 0, truck, starting from rest, moves in the positive x-direction at uniform acceleration of 5 ms^$$-$$2. At t = 20 s, a ball is released from the top of the truck. The ball strikes the ground in 1 s after the release. The velocity of the ball, when it strikes the ground, will be :

(Given g = 10 ms^$$-$$2)

Two projectiles P₁ and P₂ thrown with speed in the ratio $$\sqrt3$$ : $$\sqrt2$$, attain the same height during their motion. If P₂ is thrown at an angle of 60$$^\circ$$ with the horizontal, the angle of projection of P₁ with horizontal will be :

A person can throw a ball upto a maximum range of 100 m. How high above the ground he can throw the same ball?

A projectile is launched at an angle '$$\alpha$$' with the horizontal with a velocity 20 ms^$$-$$1. After 10 s, its inclination with horizontal is '$$\beta$$'. The value of tan$$\beta$$ will be : (g = 10 ms^$$-$$2).

A girl standing on road holds her umbrella at 45$$^\circ$$ with the vertical to keep the rain away. If she starts running without umbrella with a speed of 15$$\sqrt2$$ kmh^$$-$$1, the rain drops hit her head vertically. The speed of rain drops with respect to the moving girl is :

Given below are two statements. One is labelled as Assertion A and the other is labelled as Reason R.

Assertion A : Two identical balls A and B thrown with same velocity 'u' at two different angles with horizontal attained the same range R. IF A and B reached the maximum height h₁ and h₂ respectively, then $$R = 4\sqrt {{h_1}{h_2}} $$

Reason R : Product of said heights.

$${h_1}{h_2} = \left( {{{{u^2}{{\sin }^2}\theta } \over {2g}}} \right)\,.\,\left( {{{{u^2}{{\cos }^2}\theta } \over {2g}}} \right)$$

Choose the correct answer :

A projectile is projected with velocity of 25 m/s at an angle $$\theta$$ with the horizontal. After t seconds its inclination with horizontal becomes zero. If R represents horizontal range of the projectile, the value of $$\theta$$ will be :

[use g = 10 m/s²]

The maximum speed of a boat in still water is 27 km/h. Now this boat is moving downstream in a river flowing at 9 km/h. A man in the boat throws a ball vertically upwards with speed of 10 m/s. Range of the ball as observed by an observer at rest on the bank is __________ cm. (Take $g=10$ m/s²)

A particle is projected at an angle of $30^{\circ}$ from horizontal at a speed of $60 \mathrm{~m} / \mathrm{s}$. The height traversed by the particle in the first second is $\mathrm{h}_0$ and height traversed in the last second, before it reaches the maximum height, is $h_1$. The ratio $h_0: h_1$ is __________.

[Take, $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$ ]

A body of mass M thrown horizontally with velocity v from the top of the tower of height H touches the ground at a distance of $$100 \mathrm{~m}$$ from the foot of the tower. A body of mass $$2 \mathrm{~M}$$ thrown at a velocity $$\frac{v}{2}$$ from the top of the tower of height $$4 \mathrm{H}$$ will touch the ground at a distance of _______ m.

The maximum height reached by a projectile is $$64 \mathrm{~m}$$. If the initial velocity is halved, the new maximum height of the projectile is ______ $$\mathrm{m}$$.

A ball rolls off the top of a stairway with horizontal velocity $$u$$. The steps are $$0.1 \mathrm{~m}$$ high and $$0.1 \mathrm{~m}$$ wide. The minimum velocity $$u$$ with which that ball just hits the step 5 of the stairway will be $$\sqrt{x} \mathrm{~ms}^{-1}$$ where $$x=$$ __________ [use $$\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$$ ].

A particle starts from origin at $$t=0$$ with a velocity $$5 \hat{i} \mathrm{~m} / \mathrm{s}$$ and moves in $$x-y$$ plane under action of a force which produces a constant acceleration of $$(3 \hat{i}+2 \hat{j}) \mathrm{m} / \mathrm{s}^2$$. If the $$x$$-coordinate of the particle at that instant is $$84 \mathrm{~m}$$, then the speed of the particle at this time is $$\sqrt{\alpha} \mathrm{~m} / \mathrm{s}$$. The value of $$\alpha$$ is _________.

A projectile fired at $$30^{\circ}$$ to the ground is observed to be at same height at time $$3 \mathrm{~s}$$ and $$5 \mathrm{~s}$$ after projection, during its flight. The speed of projection of the projectile is ___________ $$\mathrm{m} ~\mathrm{s}^{-1}$$.

(Given $$g=10 \mathrm{~ms}^{-2}$$ )

The speed of a swimmer is $$4 \mathrm{~km} \mathrm{~h}^{-1}$$ in still water. If the swimmer makes his strokes normal to the flow of river of width $$1 \mathrm{~km}$$, he reaches a point $$750 \mathrm{~m}$$ down the stream on the opposite bank.

The speed of the river water is ___________ $$\mathrm{km} ~\mathrm{h}^{-1}$$

An object is projected in the air with initial velocity u at an angle $$\theta$$. The projectile motion is such that the horizontal range R, is maximum. Another object is projected in the air with a horizontal range half of the range of first object. The initial velocity remains same in both the case. The value of the angle of projection, at which the second object is projected, will be _________ degree.

A ball of mass m is thrown vertically upward. Another ball of mass $$2 \mathrm{~m}$$ is thrown at an angle $$\theta$$ with the vertical. Both the balls stay in air for the same period of time. The ratio of the heights attained by the two balls respectively is $$\frac{1}{x}$$. The value of x is _____________.

If the initial velocity in horizontal direction of a projectile is unit vector $$\hat{i}$$ and the equation of trajectory is $$y=5 x(1-x)$$. The $$y$$ component vector of the initial velocity is ______________ $$\hat{j}$$. ($$\mathrm{Take}$$ $$\left.\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}\right)$$

A fighter jet is flying horizontally at a certain altitude with a speed of 200 ms^$$-$$1. When it passes directly overhead an anti-aircraft gun, a bullet is fired from the gun, at an angle $$\theta$$ with the horizontal, to hit the jet. If the bullet speed is 400 m/s, the value of $$\theta$$ will be ___________$$^\circ$$.

A body is projected from the ground at an angle of 45$$^\circ$$ with the horizontal. Its velocity after 2s is 20 ms^$$-$$1. The maximum height reached by the body during its motion is __________ m. (use g = 10 ms^$$-$$2)